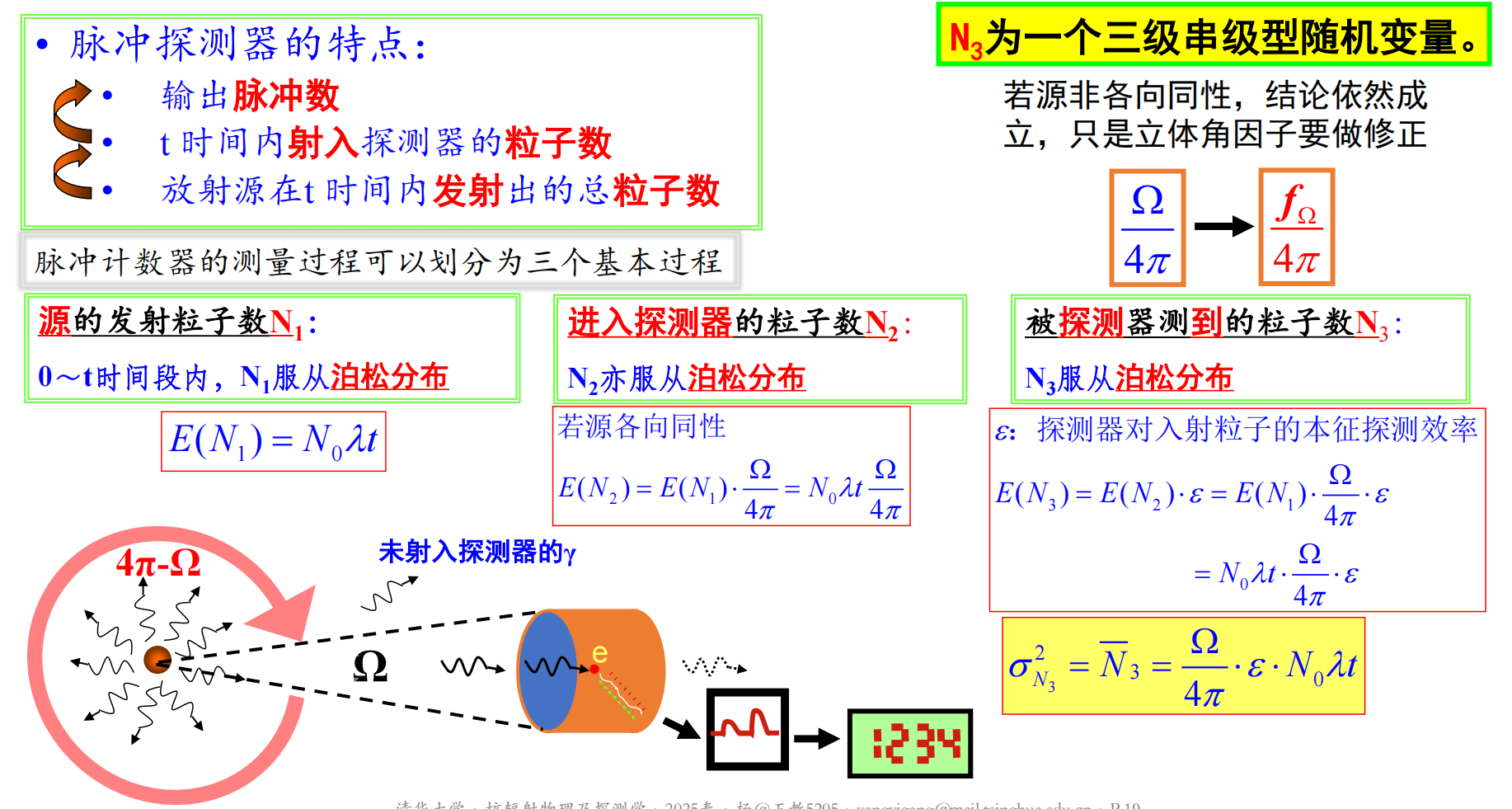
注:可从清华大学GitLab 获取量子力学笔记markdown源文件。
de Broglie(1923)提出实物粒子(静质量 m ≠ 0 m\ne0 m = 0 波粒二象性 的假设,即与动量为 p p p E E E λ \lambda λ ν \nu ν
λ = h p , ν = E h \lambda = \frac{h}{p}, \kern 12pt \nu = \frac{E}{h} λ = p h , ν = h E
并称之为物质波 。
以电子为例,它是粒子和波动两重性矛盾的统一,但这个波不再是经典概念下的波 ,粒子也不再是经典概念中的粒子 。
指微观粒子与物质相互作用时的“颗粒性 ”(corpuscularity)或“原子性 ”(atomicity),具有集中的能量E E E p ⃗ \vec{p}\ p
但与经典的粒子不同,微观粒子没有确定的轨道 ,而应采用“概率 ”的概念。
指微观粒子在空间传播时的“相干 (coherent)叠加性 ”,有“干涉 ”、“衍射 ”、“偏振 ”等现象,具有波长λ \lambda λ k ⃗ \vec{k}\ k
但与经典的波不同,没有某种实际物理量(如质点的位移、电场、磁场)的波动分布.
经典力学中的质点由 r ⃗ \vec{r}, r p ⃗ ( v ⃗ ) \vec{p}(\vec{v}) p ( v )
每一时刻该二量具有完全确定的值,且随时间连续变化;
质点的其他力学量(E k , V , L ⃗ E_k,V,\vec{L}, E k , V , L r ⃗ \vec{r}, r p ⃗ \vec{p}, p r ⃗ \vec{r}, r p ⃗ \vec{p}, p
质点状态的变化遵从牛顿定律:若已知 r ⃗ 0 \vec{r}_0 r 0 p ⃗ 0 \vec{p}_0 p 0 r ⃗ ( t ) \vec{r}(t) r ( t ) p ⃗ ( t ) \vec{p}(t) p ( t )
{ v ⃗ ( t ) = ∫ 0 t F ⃗ m d t + v ⃗ 0 p ⃗ ( t ) = ∫ 0 t F ⃗ d t + p ⃗ 0 r ⃗ ( t ) = ∫ 0 t v ⃗ ( t ) d t + r ⃗ 0 \left{\begin{matrix} \vec{v}(t) = \int_0^t \frac{\vec{F}}{m}\mathrm{d}t + \vec{v}_0 \\ \vec{p}(t) = \int_0^t \vec{F}\mathrm{d}t + \vec{p}_0 \\ \vec{r}(t) = \int_0^t \vec{v}(t)\mathrm{d}t + \vec{r}_0 \end{matrix}\right. ⎩ ⎨ ⎧ v ( t ) = ∫ 0 t m F d t + v 0 p ( t ) = ∫ 0 t F d t + p 0 r ( t ) = ∫ 0 t v ( t ) d t + r 0
r ⃗ ( t ) \vec{r}(t) r ( t )
量子力学中微观粒子的状态由波函数 (wave function)描写:
微观粒子不可能同时具有确定的 r ⃗ \vec{r}, r p ⃗ \vec{p}, p 没有确定的轨道 ;
对于一般状态的微观粒子,应该用一般的时间和空间的复函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) 波函数 (亦称态矢量 )。波函数是在空间的一个分布(在给定时间 t t t ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r )
波函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t )
波函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) Schrödinger方程 。
M.Born(1926)提出的概率波 把微观粒子的“原子性 ”与波的“相干叠加性 ”统一在了一起。
量子力学假定之一:一个微观粒子的状态总可以用一个波函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) ∣ ψ ( r ⃗ , t ) ∣ 2 |\psi(\vec{r},t)|^2 ∣ ψ ( r , t ) ∣ 2 概率密度 。波函数本身称为概率波幅 (probability amplitude).
∣ ψ ( r ⃗ , t ) ∣ 2 Δ x Δ y Δ z |\psi(\vec{r},t)|^2\Delta x\Delta y\Delta z ∣ ψ ( r , t ) ∣ 2 Δ x Δ y Δ z r ⃗ \vec{r}, r Δ x Δ y Δ z \Delta x\Delta y\Delta z Δ x Δ y Δ z
对于概率分布来说,重要的是相对概率分布 ,所以将波函数乘以一个常数,它仍然描写量子体系的同一个状态。即对于任意非零常数 C C C ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) C ψ ( r ⃗ , t ) C\psi(\vec{r},t) C ψ ( r , t ) 常数因子不确定性 。
根据波函数的统计诠释,很自然要求微观粒子(不产生,不湮没)在空间各点的概率之总和为 1 1 1 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) 归一化条件 :
∫ ( 全 ) ∣ ψ ( r ⃗ , t ) ∣ 2 d 3 r = 1 \int_{(全)} \left|\psi(\vec{r},t)\right|^2 \mathrm{d}^3r = 1 ∫ ( 全 ) ∣ ψ ( r , t ) ∣ 2 d 3 r = 1
一般的,若波函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) 平方可积 条件,即存在有限正常数 A A A
∫ ( 全 ) ∣ ψ ( r ⃗ , t ) ∣ 2 d 3 r = A \int_{(全)} \left|\psi(\vec{r},t)\right|^2 \mathrm{d}^3r = A ∫ ( 全 ) ∣ ψ ( r , t ) ∣ 2 d 3 r = A
则有
∫ ( 全 ) ∣ 1 A ψ ( r ⃗ , t ) ∣ 2 d 3 r = 1 \int_{(全)} \left|\frac{1}{\sqrt{A}}\psi(\vec{r},t)\right|^2 \mathrm{d}^3r = 1 ∫ ( 全 ) A 1 ψ ( r , t ) 2 d 3 r = 1
应当注意,即使加上归一化条件,波函数仍有相位 (phase)不定性 ,即假设 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) e i δ ψ ( r ⃗ , t ) \mathrm{e}^{\mathrm{i}\delta}\psi(\vec{r},t) e i δ ψ ( r , t )
对于某些理想(非物理)的情况,波函数是不能归一的,例如平面波(自由粒子的波函数):ψ ( r ⃗ , t ) = A e i ℏ ( p ⃗ ⋅ r ⃗ − E t ) \psi(\vec{r},t) = A\mathrm{e}^{\frac{\mathrm{i}}{\hbar}\left(\vec{p}\cdot\vec{r}-Et\right)} ψ ( r , t ) = A e ℏ i ( p ⋅ r − Et )
平面波是理想模型,实际上应该用“波包 ”来描述自由粒子,即粒子分布在有限空间 ,例如分布在 − L 2 ≤ x ≤ L 2 -\frac{L}{2} \le x \le \frac{L}{2} − 2 L ≤ x ≤ 2 L
ψ p ( x ) = 1 L e i ℏ p x \psi_p(x) = \frac{1}{\sqrt{L}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}px} ψ p ( x ) = L 1 e ℏ i p x
其称为箱归一化的平面波,满足
∫ − L 2 L 2 ∣ ψ p ( x ) ∣ 2 d x = 1 \int_{-\frac{L}{2}}^{\frac{L}{2}} \left|\psi_p(x)\right|^2 \mathrm{d}x = 1 ∫ − 2 L 2 L ∣ ψ p ( x ) ∣ 2 d x = 1
对于三维的情况,用 Ω \Omega Ω
ψ p ⃗ ( r ⃗ ) = 1 Ω e i ℏ p ⃗ ⋅ x ⃗ \psi_{\vec{p}}(\vec{r}) = \frac{1}{\sqrt{\Omega}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\vec{p}\cdot\vec{x}} ψ p ( r ) = Ω 1 e ℏ i p ⋅ x
满足
∫ Ω ∣ ψ p ⃗ ( r ⃗ ) ∣ 2 d 3 r = 1 \int_{\Omega} \left|\psi_{\vec{p}}(\vec{r})\right|^2 \mathrm{d}^3r = 1 ∫ Ω ∣ ψ p ( r ) ∣ 2 d 3 r = 1
为处理连续谱本征函数的“归一化”,Dirac引进了 δ \delta δ
δ ( x ) = { 0 , x ≠ 0 ∞ , x = 0 \delta(x) = \begin{cases} 0, & x \ne 0 \ \infty, & x = 0 \end{cases} δ ( x ) = { 0 , ∞ , x = 0 x = 0
∫ − ε ε δ ( x ) d x = ∫ − ∞ + ∞ δ ( x ) d x = 1 ( ε > 0 ) \int_{-\varepsilon}^{\varepsilon} \delta(x) \mathrm{d}x = \int_{-\infty}^{+\infty} \delta(x) \mathrm{d}x = 1 \kern 12pt \left( \varepsilon > 0 \right) ∫ − ε ε δ ( x ) d x = ∫ − ∞ + ∞ δ ( x ) d x = 1 ( ε > 0 )
或等价的表示为:对于在 x = x 0 x = x_0 x = x 0 f ( x ) f(x) f ( x )
∫ − ∞ + ∞ f ( x ) δ ( x − x 0 ) d x = f ( x 0 ) \int_{-\infty}^{+\infty} f(x)\delta(x-x_0) \mathrm{d}x = f(x_0) ∫ − ∞ + ∞ f ( x ) δ ( x − x 0 ) d x = f ( x 0 )
δ \delta δ
δ ( x ) = 1 2 π ∫ − ∞ + ∞ e ± i k x d k \delta(x) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} \mathrm{e}^{\pm\mathrm{i}kx} \mathrm{d}k δ ( x ) = 2 π 1 ∫ − ∞ + ∞ e ± i k x d k
δ ( x ) = 1 2 π ℏ ∫ − ∞ + ∞ e ± i ℏ p x d p \delta(x) = \frac{1}{2\pi\hbar} \int_{-\infty}^{+\infty} \mathrm{e}^{\pm\frac{\mathrm{i}}{\hbar}px} \mathrm{d}p δ ( x ) = 2 π ℏ 1 ∫ − ∞ + ∞ e ± ℏ i p x d p
δ ( − x ) = δ ( x ) \delta(-x) = \delta(x) δ ( − x ) = δ ( x )
δ ( a x ) = 1 ∣ a ∣ δ ( x ) \delta(ax) = \frac{1}{|a|} \delta(x) δ ( a x ) = ∣ a ∣ 1 δ ( x )
x δ ( x − a ) = a δ ( x − a ) x\delta(x-a) = a\delta(x-a) x δ ( x − a ) = a δ ( x − a )
δ \delta δ
ψ p ( x ) = 1 2 π ℏ e i ℏ p x \psi_p(x) = \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}px} ψ p ( x ) = 2 π ℏ 1 e ℏ i p x
其满足 δ \delta δ
∫ − ∞ + ∞ ψ p ′ ∗ ( x ) ψ p ( x ) d x = 1 2 π ℏ ∫ − ∞ + ∞ e i ℏ ( p − p ′ ) x d x = δ ( p − p ′ ) \int_{-\infty}^{+\infty} \psi^*{p'}(x), \psi_p(x), \mathrm{d}x = \frac{1}{2\pi\hbar} \int {-\infty}^{+\infty} e^{\frac{\mathrm{i}}{\hbar}(p-p')x} \mathrm{d}x = \delta(p-p') ∫ − ∞ + ∞ ψ p ′ ∗ ( x ) ψ p ( x ) d x = 2 π ℏ 1 ∫ − ∞ + ∞ e ℏ i ( p − p ′ ) x d x = δ ( p − p ′ )
对于三维的情况,波函数
ψ p ⃗ ( r ⃗ ) = 1 ( 2 π ℏ ) 3 2 e i ℏ p ⃗ ⋅ r ⃗ \psi_{\vec{p}}(\vec{r}) = \frac{1}{\left(2\pi\hbar\right)^{\frac{3}{2}}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\vec{p}\cdot\vec{r}} ψ p ( r ) = ( 2 π ℏ ) 2 3 1 e ℏ i p ⋅ r
其满足 δ \delta δ
∫ − ∞ + ∞ ψ p ⃗ ′ ∗ ( r ⃗ ) ψ p ⃗ ( r ⃗ ) d 3 r = δ ( p ⃗ − p ⃗ ′ ) = δ ( p x − p x ′ ) δ ( p y − p y ′ ) δ ( p z − p z ′ ) \int_{-\infty}^{+\infty} \psi^*{\vec{p}\ '}(\vec{r}), \psi {\vec{p}}(\vec{r}), \mathrm{d}^3r = \delta(\vec{p}-\vec{p}\ ') = \delta(p_x-p'_x) \delta(p_y-p'_y) \delta(p_z-p'_z) ∫ − ∞ + ∞ ψ p ′ ∗ ( r ) ψ p ( r ) d 3 r = δ ( p − p ′ ) = δ ( p x − p x ′ ) δ ( p y − p y ′ ) δ ( p z − p z ′ )
对于 N N N
ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N ) \psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N) ψ ( r 1 , r 2 , ⋯ , r N )
其中 r ⃗ 1 ( x 1 , y 1 , z 1 ) , r ⃗ 2 ( x 2 , y 2 , z 2 ) , ⋯ , r ⃗ N ( x N , y N , z N ) \vec{r}_1(x_1,y_1,z_1),\vec{r}_2(x_2,y_2,z_2),\cdots,\vec{r}_N(x_N,y_N,z_N) r 1 ( x 1 , y 1 , z 1 ) , r 2 ( x 2 , y 2 , z 2 ) , ⋯ , r N ( x N , y N , z N ) 3 N 3N 3 N
∣ ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N ) ∣ 2 d 3 r 1 d 3 r 2 ⋯ d 3 r N \left|\psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N)\right|^2 \mathrm{d}^3r_1 \mathrm{d}^3r_2 \cdots \mathrm{d}^3r_N ∣ ψ ( r 1 , r 2 , ⋯ , r N ) ∣ 2 d 3 r 1 d 3 r 2 ⋯ d 3 r N
表示粒子 1 1 1 ( r ⃗ 1 , r ⃗ 1 + d r ⃗ 1 ) (\vec{r}_1,\vec{r}_1+\mathrm{d}\vec{r}_1) ( r 1 , r 1 + d r 1 ) 2 2 2 ( r ⃗ 2 , r ⃗ 2 + d r ⃗ 2 ) (\vec{r}_2,\vec{r}_2+\mathrm{d}\vec{r}_2) ( r 2 , r 2 + d r 2 ) N N N ( r ⃗ N , r ⃗ N + d r ⃗ N ) (\vec{r}_N,\vec{r}_N+\mathrm{d}\vec{r}_N) ( r N , r N + d r N )
∫ ( 全 ) ∣ ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N ) ∣ 2 d 3 r 1 d 3 r 2 ⋯ d 3 r N = 1 \int_{(全)} \left|\psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N)\right|^2 \mathrm{d}^3r_1 \mathrm{d}^3r_2 \cdots \mathrm{d}^3r_N = 1 ∫ ( 全 ) ∣ ψ ( r 1 , r 2 , ⋯ , r N ) ∣ 2 d 3 r 1 d 3 r 2 ⋯ d 3 r N = 1
一般来说 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r )
∫ ( 全 ) ∣ ψ ( r ⃗ ) ∣ 2 d 3 r = 有限正常数 \int_{(全)} \left|\psi(\vec{r})\right|^2 \mathrm{d}^3r = 有限正常数 ∫ ( 全 ) ∣ ψ ( r ) ∣ 2 d 3 r = 有限正常数
可以存在有限个孤立奇点。
一个真实的波函数需要满足归一化条件
∫ ( 全 ) ∣ ψ ( r ⃗ ) ∣ 2 d 3 r = 1 \int_{(全)} \left|\psi(\vec{r})\right|^2 \mathrm{d}^3r = 1 ∫ ( 全 ) ∣ ψ ( r ) ∣ 2 d 3 r = 1
但在量子力学中并不排除使用某些不能归一化的理想的波函数,如平面波 ψ ( r ⃗ ) ∼ e i ℏ p ⃗ ⋅ r ⃗ \psi(\vec{r}) \sim e^{\frac{\mathrm{i}}{\hbar}\vec{p}\cdot\vec{r}} ψ ( r ) ∼ e ℏ i p ⋅ r δ \delta δ ψ ( r ⃗ ) ∼ δ ( r ⃗ ) \psi(\vec{r}) \sim \delta(\vec{r}) ψ ( r ) ∼ δ ( r )
要求 ∣ ψ ( r ⃗ ) ∣ 2 |\psi(\vec{r})|^2 ∣ ψ ( r ) ∣ 2 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r )
波函数 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r ) V ( r ⃗ ) V(\vec{r}) V ( r )
波函数 ψ \psi ψ ϕ \phi ϕ
( ψ , ϕ ) = ∫ − ∞ + ∞ ψ ∗ ( x ) ϕ ( x ) d x \left(\psi,\phi\right) = \int_{-\infty}^{+\infty} \psi^*(x)\phi(x) \mathrm{d}x ( ψ , ϕ ) = ∫ − ∞ + ∞ ψ ∗ ( x ) ϕ ( x ) d x
内积是态矢空间中两个态矢量的“点乘”,是一个复数 ,其有以下性质:
( ψ , ψ ) ≥ 0 \left(\psi,\psi\right) \ge 0 ( ψ , ψ ) ≥ 0
( ψ , ϕ ) = ( ϕ , ψ ) ∗ = ( ϕ ∗ , ψ ∗ ) \left(\psi,\phi\right) = \left(\phi,\psi\right)^* = \left(\phi^,\psi^ \right) ( ψ , ϕ ) = ( ϕ , ψ ) ∗ = ( ϕ ∗ , ψ ∗ )
( ψ , C 1 ϕ 1 + C 2 ϕ 2 ) = C 1 ( ψ , ϕ 1 ) + C 2 ( ψ , ϕ 2 ) \left(\psi,C_1\phi_1+C_2\phi_2\right) = C_1\left(\psi,\phi_1\right) + C_2\left(\psi,\phi_2\right) ( ψ , C 1 ϕ 1 + C 2 ϕ 2 ) = C 1 ( ψ , ϕ 1 ) + C 2 ( ψ , ϕ 2 )
( C 1 ψ 1 + C 2 ψ 2 , ϕ ) = C 1 ∗ ( ψ 1 , ϕ ) + C 2 ∗ ( ψ 2 , ϕ ) \left(C_1\psi_1+C_2\psi_2,\phi\right) = C_1^\left(\psi_1,\phi\right) + C_2^ \left(\psi_2,\phi\right) ( C 1 ψ 1 + C 2 ψ 2 , ϕ ) = C 1 ∗ ( ψ 1 , ϕ ) + C 2 ∗ ( ψ 2 , ϕ )
特别的,内积没有对称性 ,即一般
( ψ , ϕ ) = ( ϕ , ψ ) ∗ ≠ ( ϕ , ψ ) \left(\psi,\phi\right) = \left(\phi,\psi\right)^* \ne \left(\phi,\psi\right) ( ψ , ϕ ) = ( ϕ , ψ ) ∗ = ( ϕ , ψ )
当 ( ψ , ϕ ) = 0 \left(\psi,\phi\right) = 0 ( ψ , ϕ ) = 0 ψ \psi ψ ϕ \phi ϕ 正交 。
使用 ∫ ( 全 ) d τ \int_{(全)} \mathrm{d}\tau ∫ ( 全 ) d τ
对于一维粒子
∫ ( 全 ) d τ = ∫ − ∞ + ∞ d x \int_{(全)} \mathrm{d}\tau = \int_{-\infty}^{+\infty} \mathrm{d}x ∫ ( 全 ) d τ = ∫ − ∞ + ∞ d x
对于三维粒子
∫ ( 全 ) d τ = ∫ − ∞ + ∞ ∫ − ∞ + ∞ ∫ − ∞ + ∞ d x d y d z \int_{(全)} \mathrm{d}\tau = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \mathrm{d}x \mathrm{d}y \mathrm{d}z ∫ ( 全 ) d τ = ∫ − ∞ + ∞ ∫ − ∞ + ∞ ∫ − ∞ + ∞ d x d y d z
对于 N N N
∫ ( 全 ) d τ = ∫ − ∞ + ∞ ⋯ ∫ − ∞ + ∞ d x 1 d y 1 d z 1 ⋯ d x N d y N d z N \int_{(全)} \mathrm{d}\tau = \int_{-\infty}^{+\infty} \cdots \int_{-\infty}^{+\infty} \mathrm{d}x_1 \mathrm{d}y_1 \mathrm{d}z_1 \cdots \mathrm{d}x_N \mathrm{d}y_N \mathrm{d}z_N ∫ ( 全 ) d τ = ∫ − ∞ + ∞ ⋯ ∫ − ∞ + ∞ d x 1 d y 1 d z 1 ⋯ d x N d y N d z N
在内积的定义下,有
( ψ , ψ ) = ∫ ( 全 ) d τ ψ ∗ ψ = ∫ ( 全 ) d τ ∣ ψ ∣ 2 \left(\psi,\psi\right) = \int_{(全)} \mathrm{d}\tau \psi^*\psi = \int_{(全)} \mathrm{d}\tau |\psi|^2 ( ψ , ψ ) = ∫ ( 全 ) d τ ψ ∗ ψ = ∫ ( 全 ) d τ ∣ ψ ∣ 2
这样就可以简单的表示归一化条件为
( ψ , ψ ) = 1 \left(\psi,\psi\right) = 1 ( ψ , ψ ) = 1
与 ∣ ψ ( r ⃗ ) ∣ 2 |\psi(\vec{r})|^2 ∣ ψ ( r ) ∣ 2 ∣ φ ( p ⃗ ) ∣ 2 |\varphi(\vec{p})|^2 ∣ φ ( p ) ∣ 2 动量分布的概率密度 ,(归一化后)粒子动量在 ( p ⃗ , p ⃗ + d p ⃗ ) (\vec{p},\vec{p}+\mathrm{d}\vec{p}) ( p , p + d p ) ∣ φ ( p ⃗ ) ∣ 2 d 3 p |\varphi(\vec{p})|^2 \mathrm{d}^3p ∣ φ ( p ) ∣ 2 d 3 p
粒子的量子态,既可以用 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r ) φ ( p ⃗ ) \varphi(\vec{p}) φ ( p ) 同一个量子态 ,只不过表象 (representation)不同而已。称 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r ) 坐标表象 中的表示,而 φ ( p ⃗ ) \varphi(\vec{p}) φ ( p ) 动量表象 中的表示。
波函数 ψ \psi ψ φ \varphi φ Fourier变换 ,在一维情形下
φ ( p ) = 1 ( 2 π ℏ ) 1 2 ∫ − ∞ + ∞ ψ ( x ) e − i ℏ p x d x \varphi(p) = \frac{1}{(2\pi\hbar)^{\frac{1}{2}}} \int_{-\infty}^{+\infty} \psi(x)\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}px}\ \mathrm{d}x φ ( p ) = ( 2 π ℏ ) 2 1 1 ∫ − ∞ + ∞ ψ ( x ) e − ℏ i p x d x
ψ ( x ) = 1 ( 2 π ℏ ) 1 2 ∫ − ∞ + ∞ φ ( p ) e i ℏ p x d p \psi(x) = \frac{1}{(2\pi\hbar)^{\frac{1}{2}}} \int_{-\infty}^{+\infty} \varphi(p)\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}px}\ \mathrm{d}p ψ ( x ) = ( 2 π ℏ ) 2 1 1 ∫ − ∞ + ∞ φ ( p ) e ℏ i p x d p
在三维情形下
φ ( p ⃗ ) = 1 ( 2 π ℏ ) 3 2 ∫ − ∞ + ∞ ψ ( r ⃗ ) e − i ℏ p ⃗ ⋅ r ⃗ d 3 r \varphi(\vec{p}) = \frac{1}{(2\pi\hbar)^{\frac{3}{2}}} \int_{-\infty}^{+\infty} \psi(\vec{r})\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\vec{p}\cdot\vec{r}}\ \mathrm{d}^3r φ ( p ) = ( 2 π ℏ ) 2 3 1 ∫ − ∞ + ∞ ψ ( r ) e − ℏ i p ⋅ r d 3 r
ψ ( r ⃗ ) = 1 ( 2 π ℏ ) 3 2 ∫ − ∞ + ∞ φ ( p ⃗ ) e i ℏ p ⃗ ⋅ r ⃗ d 3 p \psi(\vec{r}) = \frac{1}{(2\pi\hbar)^{\frac{3}{2}}} \int_{-\infty}^{+\infty} \varphi(\vec{p})\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\vec{p}\cdot\vec{r}}\ \mathrm{d}^3p ψ ( r ) = ( 2 π ℏ ) 2 3 1 ∫ − ∞ + ∞ φ ( p ) e ℏ i p ⋅ r d 3 p
可以推得,两种表象上的波函数的归一化是等价的,即
( ψ , ψ ) = ( φ , φ ) \left(\psi,\psi\right) = \left(\varphi,\varphi\right) ( ψ , ψ ) = ( φ , φ )
( ψ , ψ ) = 1 ⟺ ( φ , φ ) = 1 \left(\psi,\psi\right) = 1 \Longleftrightarrow \left(\varphi,\varphi\right) = 1 ( ψ , ψ ) = 1 ⟺ ( φ , φ ) = 1
算符代表对波函数的某种作用或运算。
粒子处于波函数 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r ) 确定的概率分布 ,因而有确定的平均值 (又叫期待值 )。在任意状态 ψ \psi ψ A A A
A ˉ = ( ψ , A ^ ψ ) ( ψ , ψ ) \bar{A} = \frac{(\psi,\hat{A}\psi)}{(\psi,\psi)} A ˉ = ( ψ , ψ ) ( ψ , A ^ ψ )
其中 A ^ \hat{A} A ^ A A A
A ˉ = ( ψ , A ^ ψ ) \bar{A} = (\psi,\hat{A}\psi) A ˉ = ( ψ , A ^ ψ )
在波函数 ψ \psi ψ x x x
x ˉ = ∫ − ∞ + ∞ ∣ ψ ( r ⃗ ) ∣ 2 x d 3 r = ∫ − ∞ + ∞ ψ ∗ ( r ⃗ ) x ψ ( r ⃗ ) d 3 r \bar{x} = \int_{-\infty}^{+\infty} \left|\psi(\vec{r})\right|^2, x, \mathrm{d}^3r = \int_{-\infty}^{+\infty} \psi^*(\vec{r}), x, \psi(\vec{r}), \mathrm{d}^3r x ˉ = ∫ − ∞ + ∞ ∣ ψ ( r ) ∣ 2 x d 3 r = ∫ − ∞ + ∞ ψ ∗ ( r ) x ψ ( r ) d 3 r
可以得到坐标表象下的坐标算符为
x ^ = x \hat{x} = x x ^ = x
同理
y ^ = y , z ^ = z , r ⃗ ^ = r ⃗ \hat{y} = y, \kern 12pt \hat{z} = z, \kern 12pt \hat{\vec{r}} = \vec{r} y ^ = y , z ^ = z , r ^ = r
如果状态用动量表象波函数 φ ( p ⃗ ) \varphi(\vec{p}) φ ( p )
p ⃗ ˉ = ∫ − ∞ + ∞ ∣ φ ( p ⃗ ) ∣ 2 p ⃗ d 3 p = ∫ − ∞ + ∞ φ ∗ ( p ⃗ ) p ⃗ φ ( p ⃗ ) d 3 p \bar{\vec{p}} = \int_{-\infty}^{+\infty} \left|\varphi(\vec{p})\right|^2, \vec{p}, \mathrm{d}^3p = \int_{-\infty}^{+\infty} \varphi^*(\vec{p}), \vec{p}, \varphi(\vec{p}), \mathrm{d}^3p p ˉ = ∫ − ∞ + ∞ ∣ φ ( p ) ∣ 2 p d 3 p = ∫ − ∞ + ∞ φ ∗ ( p ) p φ ( p ) d 3 p
可以得到动量表象下的动量算符为
p ⃗ ^ = p ⃗ , p ^ x = p x , p ^ y = p y , p ^ z = p z \hat{\vec{p}} = \vec{p}, \kern 12pt \hat{p}_x = p_x, \kern 12pt \hat{p}_y = p_y, \kern 12pt \hat{p}_z = p_z p ^ = p , p ^ x = p x , p ^ y = p y , p ^ z = p z
通过表象的转换,可以推得坐标表象下的动量算符为
p ⃗ ^ = − i ℏ ∇ , p ^ x = − i ℏ ∂ ∂ x , p ^ y = − i ℏ ∂ ∂ y , p ^ z = − i ℏ ∂ ∂ z \hat{\vec{p}} = -\mathrm{i}\hbar\nabla, \kern 12pt \hat{p}_x = -\mathrm{i}\hbar \frac{\partial}{\partial x}, \kern 12pt \hat{p}_y = -\mathrm{i}\hbar \frac{\partial}{\partial y}, \kern 12pt \hat{p}_z = -\mathrm{i}\hbar \frac{\partial}{\partial z} p ^ = − i ℏ∇ , p ^ x = − i ℏ ∂ x ∂ , p ^ y = − i ℏ ∂ y ∂ , p ^ z = − i ℏ ∂ z ∂
动量表象下的坐标算符为
r ⃗ ^ = i ℏ ∂ ∂ p ⃗ , x ^ = i ℏ ∂ ∂ p x , y ^ = i ℏ ∂ ∂ p y , z ^ = i ℏ ∂ ∂ p z \hat{\vec{r}} = \mathrm{i}\hbar \frac{\partial}{\partial \vec{p}}, \kern 12pt \hat{x} = \mathrm{i}\hbar \frac{\partial}{\partial p_x}, \kern 12pt \hat{y} = \mathrm{i}\hbar \frac{\partial}{\partial p_y}, \kern 12pt \hat{z} = \mathrm{i}\hbar \frac{\partial}{\partial p_z} r ^ = i ℏ ∂ p ∂ , x ^ = i ℏ ∂ p x ∂ , y ^ = i ℏ ∂ p y ∂ , z ^ = i ℏ ∂ p z ∂
注:梯度、散度、旋度的介绍以及其在各种坐标系下的表示,可参考魏斌老师的课件 。这里给出柱坐标与球坐标下的梯度算符,
柱坐标 ( r , ϕ , z ) (r,\phi,z) ( r , ϕ , z )
∇ f = ∂ f ∂ r e ⃗ r + 1 r ∂ f ∂ θ e ⃗ θ + ∂ f ∂ z e ⃗ z \nabla f = \frac{\partial f}{\partial r}\vec{e}r + \frac{1}{r}\frac{\partial f}{\partial \theta}\vec{e} \theta + \frac{\partial f}{\partial z}\vec{e}_z ∇ f = ∂ r ∂ f e r + r 1 ∂ θ ∂ f e θ + ∂ z ∂ f e z
球坐标 ( r , θ , φ ) (r,\theta,\varphi) ( r , θ , φ )
∇ f = ∂ f ∂ r e ⃗ r + 1 r ∂ f ∂ θ e ⃗ θ + 1 r sin θ ∂ f ∂ φ e ⃗ φ \nabla f = \frac{\partial f}{\partial r}\vec{e}r + \frac{1}{r}\frac{\partial f}{\partial \theta}\vec{e} \theta + \frac{1}{r\sin\theta}\frac{\partial f}{\partial \varphi}\vec{e}_\varphi ∇ f = ∂ r ∂ f e r + r 1 ∂ θ ∂ f e θ + r sin θ 1 ∂ φ ∂ f e φ
对于有经典对应的力学量,例如动能、势能和轨道角动量,由经典力学中的函数形式假定量子力学中的算符形式,可以由坐标算符与动量算符通过运算得到,即
A = A ( r ⃗ , p ⃗ ) ⟹ A ^ = A ( r ⃗ ^ , p ⃗ ^ ) A = A(\vec{r},\vec{p}) \Longrightarrow \hat{A} = A(\hat{\vec{r}},\hat{\vec{p}}) A = A ( r , p ) ⟹ A ^ = A ( r ^ , p ^ )
如一维谐振子的能量算符
H = ( p x ) 2 2 m + 1 2 k x 2 ⟹ H ^ = ( p ^ x ) 2 2 m + 1 2 k x ^ 2 H = \frac{(p_x)^2}{2m} + \frac12kx^2 \Longrightarrow \hat{H} = \frac{(\hat{p}_x)^2}{2m} + \frac12k\hat{x}^2 H = 2 m ( p x ) 2 + 2 1 k x 2 ⟹ H ^ = 2 m ( p ^ x ) 2 + 2 1 k x ^ 2
如粒子的轨道角动量算符
L ⃗ = r ⃗ × p ⃗ ⟹ L ⃗ ^ = r ⃗ ^ × p ⃗ ^ = ∣ i ⃗ j ⃗ k ⃗ x ^ y ^ z ^ p ^ x p ^ y p ^ z ∣ \vec{L} = \vec{r} \times \vec{p} \Longrightarrow \hat{\vec{L}} = \hat{\vec{r}} \times \hat{\vec{p}} =\begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \ \hat{x} & \hat{y} & \hat{z} \ \hat{p}_x & \hat{p}_y & \hat{p}_z \end{vmatrix} L = r × p ⟹ L ^ = r ^ × p ^ = i x ^ p ^ x j y ^ p ^ y k z ^ p ^ z
L ^ x = y ^ p ^ z − z ^ p ^ y L ^ y = z ^ p ^ x − x ^ p ^ z L ^ z = x ^ p ^ y − y ^ p ^ x \hat{L}_x = \hat{y}\hat{p}_z - \hat{z}\hat{p}_y \\kern 12pt\ \hat{L}_y = \hat{z}\hat{p}_x - \hat{x}\hat{p}_z \\kern 12pt\ \hat{L}_z = \hat{x}\hat{p}_y - \hat{y}\hat{p}_x L ^ x = y ^ p ^ z − z ^ p ^ y L ^ y = z ^ p ^ x − x ^ p ^ z L ^ z = x ^ p ^ y − y ^ p ^ x
在坐标表象下,上述算符的表达式为
H ^ = − ℏ 2 2 m d 2 d x 2 + 1 2 k x 2 \hat{H} = -\frac{\hbar^2}{2m} \frac{\mathrm{d}^2}{\mathrm{d}x^2} + \frac12kx^2 H ^ = − 2 m ℏ 2 d x 2 d 2 + 2 1 k x 2
L ⃗ ^ = r ⃗ × ( − i ℏ ∇ ) = ∣ i ⃗ j ⃗ k ⃗ x y z − i ℏ ∂ ∂ x − i ℏ ∂ ∂ y − i ℏ ∂ ∂ z ∣ \hat{\vec{L}} = \vec{r} \times (-\mathrm{i}\hbar\nabla) =\begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \ x & y & z \ -\mathrm{i}\hbar \frac{\partial}{\partial x} & -\mathrm{i}\hbar \frac{\partial}{\partial y} & -\mathrm{i}\hbar \frac{\partial}{\partial z} \end{vmatrix} L ^ = r × ( − i ℏ∇ ) = i x − i ℏ ∂ x ∂ j y − i ℏ ∂ y ∂ k z − i ℏ ∂ z ∂
L ^ x = − i ℏ ( y ∂ ∂ z − z ∂ ∂ y ) L ^ y = − i ℏ ( z ∂ ∂ x − x ∂ ∂ z ) L ^ z = − i ℏ ( x ∂ ∂ y − y ∂ ∂ x ) \hat{L}_x = -\mathrm{i}\hbar (y\frac{\partial}{\partial z}-z\frac{\partial}{\partial y}) \\kern 12pt\ \hat{L}_y = -\mathrm{i}\hbar (z\frac{\partial}{\partial x}-x\frac{\partial}{\partial z}) \\kern 12pt\ \hat{L}_z = -\mathrm{i}\hbar (x\frac{\partial}{\partial y}-y\frac{\partial}{\partial x}) L ^ x = − i ℏ ( y ∂ z ∂ − z ∂ y ∂ ) L ^ y = − i ℏ ( z ∂ x ∂ − x ∂ z ∂ ) L ^ z = − i ℏ ( x ∂ y ∂ − y ∂ x ∂ )
对于已归一化的波函数,力学量 A A A
A ˉ = ∫ − ∞ + ∞ ψ ∗ ( r ⃗ ) A ( r ⃗ , − i ℏ ∇ ) ψ ( r ⃗ ) d 3 r \bar{A} = \int_{-\infty}^{+\infty} \psi^*(\vec{r}), A(\vec{r},-\mathrm{i}\hbar\nabla), \psi(\vec{r}), \mathrm{d^3}r A ˉ = ∫ − ∞ + ∞ ψ ∗ ( r ) A ( r , − i ℏ∇ ) ψ ( r ) d 3 r
A ˉ = ∫ − ∞ + ∞ φ ∗ ( p ⃗ ) A ( i ℏ ∂ ∂ p ⃗ , p ⃗ ) φ ( p ⃗ ) d 3 p \bar{A} = \int_{-\infty}^{+\infty} \varphi^*(\vec{p}), A(\mathrm{i}\hbar \frac{\partial}{\partial \vec{p}},\vec{p}), \varphi(\vec{p}), \mathrm{d^3}p A ˉ = ∫ − ∞ + ∞ φ ∗ ( p ) A ( i ℏ ∂ p ∂ , p ) φ ( p ) d 3 p
在势场 U ( r ⃗ ) U(\vec{r}) U ( r ) ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) Schrödinger波动方程 :
i ℏ ∂ ψ ∂ t = [ − ℏ 2 2 m ∇ 2 + U ( r ⃗ ) ] ψ \mathrm{i}\hbar\frac{\partial\psi}{\partial t} = \left[-\frac{\hbar^2}{2m}\nabla^2 + U(\vec{r})\right]\psi i ℏ ∂ t ∂ ψ = [ − 2 m ℏ 2 ∇ 2 + U ( r ) ] ψ
假设势能 U U U t t t 分离变量法 求解,即令
ψ ( r ⃗ , t ) = ψ ( r ⃗ ) f ( t ) \psi(\vec{r},t) = \psi(\vec{r})f(t) ψ ( r , t ) = ψ ( r ) f ( t )
代入原方程,分离变量,可得:
i ℏ f ( t ) d f d t = 1 ψ ( r ⃗ ) [ − ℏ 2 2 m ∇ 2 + U ( r ⃗ ) ] ψ ( r ⃗ ) = E \frac{\mathrm{i}\hbar}{f(t)} \frac{\mathrm{d}f}{\mathrm{d}t} = \frac{1}{\psi(\vec{r})} \left[-\frac{\hbar^2}{2m}\nabla^2 + U(\vec{r})\right] \psi(\vec{r}) = E f ( t ) i ℏ d t d f = ψ ( r ) 1 [ − 2 m ℏ 2 ∇ 2 + U ( r ) ] ψ ( r ) = E
其中 E E E t t t r ⃗ \vec{r}, r
i ℏ f ( t ) d f d t = E \frac{\mathrm{i}\hbar}{f(t)} \frac{\mathrm{d}f}{\mathrm{d}t} = E f ( t ) i ℏ d t d f = E
解得
f ( t ) ∼ e − i ℏ E t f(t) \sim \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}Et} f ( t ) ∼ e − ℏ i Et
则Schrödinger波动方程的特解为
ψ ( r ⃗ , t ) = ψ E ( r ⃗ ) e − i ℏ E t \psi(\vec{r},t) = \psi_E(\vec{r})\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}Et} ψ ( r , t ) = ψ E ( r ) e − ℏ i Et
其中 ψ E ( r ⃗ ) \psi_E(\vec{r}) ψ E ( r )
[ − ℏ 2 2 m ∇ 2 + U ( r ⃗ ) ] ψ E ( r ⃗ ) = E ψ E ( r ⃗ ) \left[-\frac{\hbar^2}{2m}\nabla^2 + U(\vec{r})\right] \psi_E(\vec{r}) = E\psi_E(\vec{r}) [ − 2 m ℏ 2 ∇ 2 + U ( r ) ] ψ E ( r ) = E ψ E ( r )
对于此不含时Schrödinger方程 (又称为定态Schrödinger方程 ),在某些条件下(特别是束缚态边条件),只有某些离散的 E E E E E E 能量本征值 (energy eigenvalue),而相应的解 ψ E ( r ⃗ ) \psi_E(\vec{r}) ψ E ( r ) 能量本征函数 (energy eigenfunction),该方程也称为势场 U ( r ⃗ ) U(\vec{r}) U ( r ) 能量本征方程 。不同的能量本征值相应的本征函数是正交归一化 的(设 E E E
( ψ E , ψ E ′ ) = δ E E ′ = { 1 , E = E ′ 0 , E ≠ E ′ (\psi_E,\psi_{E'}) = \delta_{EE'} = \begin{cases} 1, & E = E' \ 0, & E \ne E' \end{cases} ( ψ E , ψ E ′ ) = δ E E ′ = { 1 , 0 , E = E ′ E = E ′
引入Hamilton算符 H ^ \hat{H} H ^ U ( r ⃗ ) U(\vec{r}) U ( r ) H ^ = − ℏ 2 2 m ∇ 2 + U ( r ⃗ ) \hat{H} = -\frac{\hbar^2}{2m} \nabla^2 + U(\vec{r}) H ^ = − 2 m ℏ 2 ∇ 2 + U ( r ) Schrödinger方程的普遍表达 :
i ℏ ∂ ψ ∂ t = H ^ ψ \mathrm{i}\hbar \frac{\partial\psi}{\partial t} = \hat{H}\psi i ℏ ∂ t ∂ ψ = H ^ ψ
当 H ^ \hat{H} H ^ t t t 能量是守恒量 ,此时的能量本征方程 为
H ^ ψ = E ψ \hat{H}\psi = E\psi H ^ ψ = E ψ
设体系由 N N N m i ( i = 1 , 2 , 3 , ⋯ , N ) m_i\ (i=1,2,3,\cdots,N) m i ( i = 1 , 2 , 3 , ⋯ , N ) i i i U i ( r ⃗ i ) U_i(\vec{r}_i) U i ( r i ) V ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N ) V(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N) V ( r 1 , r 2 , ⋯ , r N ) ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N , t ) \psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N,t) ψ ( r 1 , r 2 , ⋯ , r N , t )
i ℏ ∂ ∂ t ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N , t ) = [ ∑ i = 1 N ( − ℏ 2 2 m i ∇ i 2 + U i ( r ⃗ i ) ) + V ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N ) ] ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N , t ) \mathrm{i}\hbar\frac{\partial}{\partial t} \psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}N,t) = \left[\sum {i=1}^N \left(-\frac{\hbar^2}{2m_i}\nabla_i^2 + U_i(\vec{r}_i)\right) + V(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N) \right] \psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N,t) i ℏ ∂ t ∂ ψ ( r 1 , r 2 , ⋯ , r N , t ) = [ i = 1 ∑ N ( − 2 m i ℏ 2 ∇ i 2 + U i ( r i ) ) + V ( r 1 , r 2 , ⋯ , r N ) ] ψ ( r 1 , r 2 , ⋯ , r N , t )
其中
∇ i 2 = ∂ 2 ∂ x i 2 + ∂ 2 ∂ y i 2 + ∂ 2 ∂ z i 2 \nabla_i^2 = \frac{\partial^2}{\partial x_i^2} + \frac{\partial^2}{\partial y_i^2} + \frac{\partial^2}{\partial z_i^2} ∇ i 2 = ∂ x i 2 ∂ 2 + ∂ y i 2 ∂ 2 + ∂ z i 2 ∂ 2
不含时Schrödinger方程表示为
E ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N , t ) = [ ∑ i = 1 N ( − ℏ 2 2 m i ∇ i 2 + U i ( r ⃗ i ) ) + V ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N ) ] ψ ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N , t ) E\psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}N,t) = \left[\sum {i=1}^N \left(-\frac{\hbar^2}{2m_i}\nabla_i^2 + U_i(\vec{r}_i)\right) + V(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N) \right] \psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N,t) E ψ ( r 1 , r 2 , ⋯ , r N , t ) = [ i = 1 ∑ N ( − 2 m i ℏ 2 ∇ i 2 + U i ( r i ) ) + V ( r 1 , r 2 , ⋯ , r N ) ] ψ ( r 1 , r 2 , ⋯ , r N , t )
在该体系中,Hamilton算符
H ^ = ∑ i = 1 N ( − ℏ 2 2 m i ∇ i 2 + U i ( r ⃗ i ) ) + V ( r ⃗ 1 , r ⃗ 2 , ⋯ , r ⃗ N ) \hat{H} = \sum_{i=1}^N \left(-\frac{\hbar^2}{2m_i}\nabla_i^2 + U_i(\vec{r}_i)\right) + V(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_N) H ^ = i = 1 ∑ N ( − 2 m i ℏ 2 ∇ i 2 + U i ( r i ) ) + V ( r 1 , r 2 , ⋯ , r N )
ρ ( r ⃗ , t ) = ∣ ψ ( r ⃗ , t ) ∣ 2 = ψ ∗ ( r ⃗ , t ) ψ ( r ⃗ , t ) \rho(\vec{r},t) = |\psi(\vec{r},t)|^2 = \psi^*(\vec{r},t)\psi(\vec{r},t) ρ ( r , t ) = ∣ ψ ( r , t ) ∣ 2 = ψ ∗ ( r , t ) ψ ( r , t )
j ⃗ ( r ⃗ , t ) = − i ℏ 2 m ( ψ ∗ ∇ ψ − ψ ∇ ψ ∗ ) = 1 2 m ( ψ ∗ p ⃗ ^ ψ − ψ p ⃗ ^ ψ ∗ ) \vec{j}(\vec{r},t) = -\frac{\mathrm{i}\hbar}{2m} (\psi^\nabla\psi - \psi\nabla\psi^ ) = \frac{1}{2m} (\psi^\hat{\vec{p}}\psi - \psi\hat{\vec{p}}\psi^ ) j ( r , t ) = − 2 m i ℏ ( ψ ∗ ∇ ψ − ψ ∇ ψ ∗ ) = 2 m 1 ( ψ ∗ p ^ ψ − ψ p ^ ψ ∗ )
∂ ρ ∂ t + ∇ ⋅ j ⃗ = 0 \frac{\partial\rho}{\partial t} + \nabla\cdot\vec{j} = 0 ∂ t ∂ ρ + ∇ ⋅ j = 0
该式对任意闭区域 τ \tau τ
d d t ∫ τ ρ d τ = − ∮ S j ⃗ ⋅ d S ⃗ \frac{\mathrm{d}}{\mathrm{d}t} \int_\tau \rho \mathrm{d}\tau = -\oint_S \vec{j} \cdot \mathrm{d}\vec{S} d t d ∫ τ ρ d τ = − ∮ S j ⋅ d S
该等式左边表示在闭区域 τ \tau τ τ \tau τ S S S τ \tau τ 概率(粒子数)守恒 。
在该积分表达式中,如果令 τ → ∞ \tau\to\infty τ → ∞
d d t ∫ ( 全 ) ρ d τ = 0 ⟹ ∫ ( 全 ) ρ d τ = C o n s t \frac{\mathrm{d}}{\mathrm{d}t} \int_{(全)} \rho \mathrm{d}\tau = 0 \Longrightarrow \int_{(全)} \rho \mathrm{d}\tau = \mathrm{Const} d t d ∫ ( 全 ) ρ d τ = 0 ⟹ ∫ ( 全 ) ρ d τ = Const
这表明粒子在全空间的总概率守恒,即粒子既未产生,也未湮没。
由于Schrödinger方程只含波函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) t = 0 t=0 t = 0 ψ ( r ⃗ , 0 ) \psi(\vec{r},0) ψ ( r , 0 ) t t t ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) 原则上就完全确定 了。
以下给出自由粒子 的初值问题的解法:
对于自由粒子,其满足如下Schrödinger方程:
i ℏ ∂ ψ ∂ t = − ℏ 2 2 m ∇ 2 ψ \mathrm{i}\hbar\frac{\partial\psi}{\partial t} = -\frac{\hbar^2}{2m}\nabla^2\psi i ℏ ∂ t ∂ ψ = − 2 m ℏ 2 ∇ 2 ψ
描述自由粒子的一般状态的波函数,具有波包的形式,可以视为许多平面单色波的叠加,即
ψ ( r ⃗ , t ) = 1 ( 2 π ℏ ) 3 2 ∫ − ∞ + ∞ φ ( p ⃗ ) e i ℏ ( p ⃗ ⋅ r ⃗ − E t ) d 3 p \psi(\vec{r},t) = \frac{1}{(2\pi\hbar)^{\frac{3}{2}}} \int_{-\infty}^{+\infty} \varphi(\vec{p})\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}(\vec{p}\cdot\vec{r}-Et)}\ \mathrm{d}^3p ψ ( r , t ) = ( 2 π ℏ ) 2 3 1 ∫ − ∞ + ∞ φ ( p ) e ℏ i ( p ⋅ r − Et ) d 3 p
式中 E = p 2 2 m E = \frac{p^2}{2m} E = 2 m p 2
ψ ( r ⃗ , 0 ) = 1 ( 2 π ℏ ) 3 2 ∫ − ∞ + ∞ φ ( p ⃗ ) e i ℏ p ⃗ ⋅ r ⃗ d 3 p \psi(\vec{r},0) = \frac{1}{(2\pi\hbar)^{\frac{3}{2}}} \int_{-\infty}^{+\infty} \varphi(\vec{p})\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\vec{p}\cdot\vec{r}}\ \mathrm{d}^3p ψ ( r , 0 ) = ( 2 π ℏ ) 2 3 1 ∫ − ∞ + ∞ φ ( p ) e ℏ i p ⋅ r d 3 p
其中 φ ( p ⃗ ) \varphi(\vec{p}) φ ( p ) ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) t t t
φ ( p ⃗ ) = 1 ( 2 π ℏ ) 3 2 ∫ − ∞ + ∞ ψ ( r ⃗ , 0 ) e − i ℏ p ⃗ ⋅ r ⃗ d 3 r \varphi(\vec{p}) = \frac{1}{(2\pi\hbar)^{\frac{3}{2}}} \int_{-\infty}^{+\infty} \psi(\vec{r},0)\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\vec{p}\cdot\vec{r}}\ \mathrm{d}^3r φ ( p ) = ( 2 π ℏ ) 2 3 1 ∫ − ∞ + ∞ ψ ( r , 0 ) e − ℏ i p ⋅ r d 3 r
即 φ ( p ⃗ ) \varphi(\vec{p}) φ ( p ) ψ ( r ⃗ , 0 ) \psi(\vec{r},0) ψ ( r , 0 )
ψ ( r ⃗ , t ) = 1 ( 2 π ℏ ) 3 ∫ − ∞ + ∞ d 3 r ′ ∫ − ∞ + ∞ d 3 p e i ℏ p ⃗ ⋅ ( r ⃗ − r ⃗ ) − i ℏ E t ψ ( r ⃗ , 0 ) \psi(\vec{r},t) = \frac{1}{(2\pi\hbar)^3} \int_{-\infty}^{+\infty} \mathrm{d}^3r' \int_{-\infty}^{+\infty} \mathrm{d}^3p\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar} \vec{p}\cdot(\vec{r}-\vec{r}) - \frac{\mathrm{i}}{\hbar} Et}\ \psi(\vec{r},0) ψ ( r , t ) = ( 2 π ℏ ) 3 1 ∫ − ∞ + ∞ d 3 r ′ ∫ − ∞ + ∞ d 3 p e ℏ i p ⋅ ( r − r ) − ℏ i Et ψ ( r , 0 )
这样,体系的初始状态 ψ ( r ⃗ , 0 ) \psi(\vec{r},0) ψ ( r , 0 ) t t t ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t )
若在初始状态( t = 0 t=0 t = 0 ψ ( r ⃗ , 0 ) = ψ E ( r ⃗ ) \psi(\vec{r},0) = \psi_E(\vec{r}) ψ ( r , 0 ) = ψ E ( r )
ψ ( r ⃗ , t ) = ψ E ( r ⃗ ) e − i ℏ E t \psi(\vec{r},t) = \psi_E(\vec{r})\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}Et} ψ ( r , t ) = ψ E ( r ) e − ℏ i Et
该波函数所描述的态,称为定态 (stationary state)(体系的能量有确定值的状态,各种力学性质不随时间而改变);由若干个能量不同的本征态叠加所形成的态称为非定态 (nonstationary state)。
ψ ( r ⃗ , t ) = ∑ E C E ψ E ( r ⃗ ) e − i ℏ E t \psi(\vec{r},t) = \sum_{E} C_E\ \psi_E(\vec{r})\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}Et} ψ ( r , t ) = E ∑ C E ψ E ( r ) e − ℏ i Et
处于定态下粒子具有以下特征:
粒子在空间的概率密度 ρ ( r ⃗ ) \rho(\vec{r}) ρ ( r ) j ⃗ ( r ⃗ ) \vec{j}(\vec{r}) j ( r )
任何(不显含 t t t
任何(不显含 t t t
Schrödinger方程是量子力学的一个基本假定 ,不能从其他更根本的假定来证明,其正确性由在各种具体情况下从方程得出的结论和实验结果比较来验证.。
Schrödinger方程是线性偏微分方程 ,满足“状态叠加原理 ”对波函数的要求,其解波函数是一个复函数。
Schrödinger方程是非相对论粒子 的、且不发生实物粒子产生和湮灭 的情况下,波函数满足的方程。
如果 ψ 1 , ψ 2 , ⋯ , ψ n \psi_1,\psi_2,\cdots,\psi_n ψ 1 , ψ 2 , ⋯ , ψ n ψ = ∑ n C n ψ n \psi = \sum_n C_n\psi_n ψ = ∑ n C n ψ n C n C_n C n
对于一个指定的量子体系,如果我们找到了它的“完备的基本状态 ”,那么任何状态都可以由这些基本状态叠加而得到。
假设粒子处于非定态
ψ ( r ⃗ , t ) = ∑ n C n ψ n ( r ⃗ ) e − i ℏ E n t \psi(\vec{r},t) = \sum_{n} C_n\ \psi_n(\vec{r})\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} ψ ( r , t ) = n ∑ C n ψ n ( r ) e − ℏ i E n t
即很多能量本征值 E n ( n = 1 , 2 , 3 , ⋯ ) E_n\ (n=1,2,3,\cdots) E n ( n = 1 , 2 , 3 , ⋯ ) ψ n \psi_n ψ n E n E_n E n ∣ C n ∣ 2 |C_n|^2 ∣ C n ∣ 2 ∑ n ∣ C n ∣ 2 = 1 \sum_n |C_n|^2 = 1 ∑ n ∣ C n ∣ 2 = 1 E n E_n E n ψ n \psi_n ψ n 量子态坍缩 ,即在测量的过程中,粒子的状态由叠加态坍缩为某一能量本征态。
在任意状态 ψ \psi ψ A A A
A ˉ = ( ψ , A ^ ψ ) ( ψ , ψ ) \bar{A} = \frac{(\psi,\hat{A}\psi)}{(\psi,\psi)} A ˉ = ( ψ , ψ ) ( ψ , A ^ ψ )
若满足归一化条件 ( ψ , ψ ) = 1 (\psi,\psi)=1 ( ψ , ψ ) = 1
A ˉ = ( ψ , A ^ ψ ) \bar{A} = (\psi,\hat{A}\psi) A ˉ = ( ψ , A ^ ψ )
若归一化的 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r ) A ^ \hat{A} A ^ A A A
ψ ( r ⃗ ) = ∑ n C n ψ n ( r ⃗ ) ( ∑ n ∣ C n ∣ 2 = 1 ) \psi(\vec{r}) = \sum_{n} C_n\ \psi_n(\vec{r}) \kern 24pt \left(\sum_n |C_n|^2 = 1\right) ψ ( r ) = n ∑ C n ψ n ( r ) ( n ∑ ∣ C n ∣ 2 = 1 )
若在每个本征态有 A ^ ψ n = A n ψ n \hat{A}\psi_n = A_n\psi_n A ^ ψ n = A n ψ n
A ˉ = ( ψ , A ^ ψ ) ( ψ , ψ ) = ( [ ∑ n C n ψ n ( r ⃗ ) ] , A ^ [ ∑ n C n ψ n ( r ⃗ ) ] ) ( [ ∑ n C n ψ n ( r ⃗ ) ] , [ ∑ n C n ψ n ( r ⃗ ) ] ) = ∑ n ∣ C n ∣ 2 A n ∑ n ∣ C n ∣ 2 = ∑ n ∣ C n ∣ 2 A n \bar{A} = \frac{(\psi,\hat{A}\psi)}{(\psi,\psi)} = \frac{([\sum_{n} C_n\ \psi_n(\vec{r})],\hat{A}[\sum_{n} C_n\ \psi_n(\vec{r})])}{([\sum_{n} C_n\ \psi_n(\vec{r})],[\sum_{n} C_n\ \psi_n(\vec{r})])} = \frac{\sum_{n} |C_n|^2 A_n}{\sum_{n} |C_n|^2} = \sum_{n} |C_n|^2 A_n A ˉ = ( ψ , ψ ) ( ψ , A ^ ψ ) = ([ ∑ n C n ψ n ( r )] , [ ∑ n C n ψ n ( r )]) ([ ∑ n C n ψ n ( r )] , A ^ [ ∑ n C n ψ n ( r )]) = ∑ n ∣ C n ∣ 2 ∑ n ∣ C n ∣ 2 A n = n ∑ ∣ C n ∣ 2 A n
本章主要是用Schrödinger方程来处理一维粒子 的能量本征态问题,一般分为两类问题:
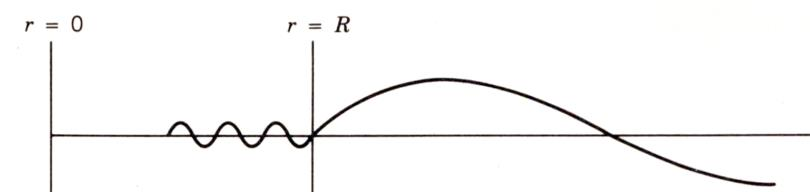
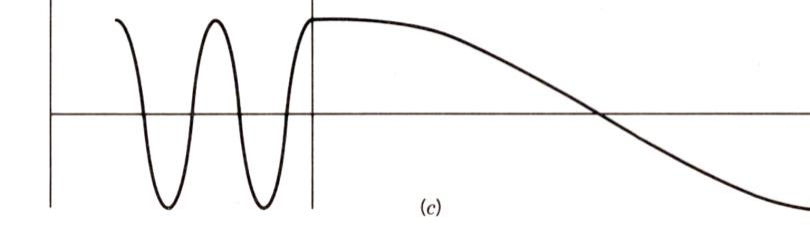
束缚态问题 :束缚态 (bound state)是指粒子局限在有限的空间中,即粒子在无穷远处出现的概率等于零的状态,即当 x → ± ∞ x\to\pm\infty x → ± ∞ ψ ( x ) → 0 \psi(x)\to0 ψ ( x ) → 0 非束缚态 (或称散射态 )指粒子可以出现在无穷远处的状态,即当 x → + ∞ x\to+\infty x → + ∞ x → − ∞ x\to-\infty x → − ∞ ψ ( x ) ≠ 0 \psi(x)\ne0 ψ ( x ) = 0 V ( x ) V(x) V ( x ) ψ ( x ) \psi(x) ψ ( x ) E E E E n E_n E n
散射问题 :会给出势场函数 V ( x ) V(x) V ( x ) E E E ψ ( x ) \psi(x) ψ ( x )
在求解上述两个问题的能量本征方程时,要根据具体物理问题的边界条件 来定解。(束缚态问题还有着 lim x → ∞ ψ ( x ) = 0 \lim_{x\to\infty}\ \psi(x)=0 lim x → ∞ ψ ( x ) = 0
如果对一个 给定的能量 E E E 一个线性独立 的波函数存在,则称该能级是非简并 的;否则 称它是简并 的,其线性独立的波函数的个数称为它的简并度 。
定义一维粒子的空间反射算符 P P P
P ψ ( x ) = ψ ( − x ) P \psi(x) = \psi(-x) P ψ ( x ) = ψ ( − x )
其对应的本征方程为
P ψ ( x ) = π ψ ( x ) P \psi(x) = \pi \psi(x) P ψ ( x ) = π ψ ( x )
定义宇称 (parity)为空间反射算符的本征值 π \pi π ± 1 \pm1 ± 1
P ψ ( x ) = ψ ( − x ) = { ψ ( x ) , π = + 1 , 偶(正)宇称 − ψ ( x ) , π = − 1 , 奇(负)宇称 P\psi(x) = \psi(-x) = \begin{cases} \psi(x), & \pi=+1, & 偶(正)宇称 \ -\psi(x), & \pi=-1, & 奇(负)宇称 \end{cases} P ψ ( x ) = ψ ( − x ) = { ψ ( x ) , − ψ ( x ) , π = + 1 , π = − 1 , 偶(正)宇称 奇(负)宇称
即空间反射不变的波函数具有偶(正)宇称 (even parity);变号的波函数具有奇(负)宇称 (odd parity);还有一些波函数没有确定的宇称,它们不是空间反射算符的本征态。
质量为 m m m x x x V ( x ) V(x) V ( x )
[ − ℏ 2 2 m d 2 d x 2 + V ( x ) ] ψ ( x ) = E ψ ( x ) \left[-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}+V(x)\right] \psi(x) = E \psi(x) [ − 2 m ℏ 2 d x 2 d 2 + V ( x ) ] ψ ( x ) = E ψ ( x )
在量子力学中,如果不作特别的声明,都认为 V ( x ) V(x) V ( x ) V ( x ) = V ∗ ( x ) V(x) = V^*(x) V ( x ) = V ∗ ( x )
设 ψ ( x ) \psi(x) ψ ( x ) E E E ψ ∗ ( x ) \psi^*(x) ψ ∗ ( x ) E E E
对定态Schrödinger方程取复共轭,可得
[ − ℏ 2 2 m d 2 d x 2 + V ( x ) ] ψ ∗ ( x ) = E ψ ∗ ( x ) \left[-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}+V(x)\right] \psi^(x) = E \psi^ (x) [ − 2 m ℏ 2 d x 2 d 2 + V ( x ) ] ψ ∗ ( x ) = E ψ ∗ ( x )
显然 ψ ∗ ( x ) \psi^*(x) ψ ∗ ( x ) E E E
假设对应于能量的某个本征值 E E E 无简并 ,则可取为实解 (除了一个无关紧要的常数因子外)。
对应于能量的某个本征值 E E E E E E 一组实解的线性叠加 。
对于能级有简并 的情况,要用到此定理;通过定理1和定理2,可以说明定态Schrödinger方程的基本解组可全取为实解。
假设 ψ ( x ) \psi(x) ψ ( x )
如果 ψ ( x ) \psi(x) ψ ( x )
如果 ψ ( x ) \psi(x) ψ ( x ) ψ ∗ ( x ) \psi^*(x) ψ ∗ ( x ) E E E
φ ( x ) = ψ ( x ) + ψ ∗ ( x ) , χ ( x ) = − i [ ψ ( x ) − ψ ∗ ( x ) ] \varphi(x) = \psi(x) + \psi^(x), \kern 1em \chi(x) = -\mathrm{i} [\psi(x) - \psi^ (x)] φ ( x ) = ψ ( x ) + ψ ∗ ( x ) , χ ( x ) = − i [ ψ ( x ) − ψ ∗ ( x )]
也是方程同属于能量 E E E φ ( x ) \varphi(x) φ ( x ) χ ( x ) \chi(x) χ ( x ) ψ ( x ) \psi(x) ψ ( x ) ψ ∗ ( x ) \psi^*(x) ψ ∗ ( x )
ψ = 1 2 ( φ + i χ ) , ψ ∗ = 1 2 ( φ − i χ ) \psi = \frac12 (\varphi + \mathrm{i} \chi), \kern 1em \psi^* = \frac12 (\varphi - \mathrm{i} \chi) ψ = 2 1 ( φ + i χ ) , ψ ∗ = 2 1 ( φ − i χ )
设势能函数 V ( x ) V(x) V ( x ) V ( x ) = V ( − x ) V(x)=V(-x) V ( x ) = V ( − x ) ψ ( x ) \psi(x) ψ ( x ) E E E ψ ( − x ) \psi(-x) ψ ( − x ) E E E
当 x ⟶ − x x\longrightarrow -x x ⟶ − x
d 2 d x 2 ⟶ d 2 d ( − x ) 2 = d 2 d x 2 , V ( x ) ⟶ V ( − x ) = V ( x ) \frac{\mathrm{d}^2}{\mathrm{d}x^2} \longrightarrow \frac{\mathrm{d}^2}{\mathrm{d}(-x)^2} = \frac{\mathrm{d}^2}{\mathrm{d}x^2}, \kern 1em V(x) \longrightarrow V(-x) = V(x) d x 2 d 2 ⟶ d ( − x ) 2 d 2 = d x 2 d 2 , V ( x ) ⟶ V ( − x ) = V ( x )
则定态Schrödinger方程转化为
[ − ℏ 2 2 m d 2 d x 2 + V ( x ) ] ψ ( − x ) = E ψ ( − x ) \left[-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}+V(x)\right] \psi(-x) = E \psi(-x) [ − 2 m ℏ 2 d x 2 d 2 + V ( x ) ] ψ ( − x ) = E ψ ( − x )
显然 ψ ( − x ) \psi(-x) ψ ( − x ) E E E
如果对应于某能量 E E E 宇称 。
因为此时 ψ ( x ) \psi(x) ψ ( x ) ψ ( − x ) \psi(-x) ψ ( − x ) π \pi π P ψ ( x ) = ψ ( − x ) = π ψ ( x ) P\psi(x) = \psi(-x) = \pi\psi(x) P ψ ( x ) = ψ ( − x ) = π ψ ( x )
设势能函数 V ( x ) V(x) V ( x ) V ( x ) = V ( − x ) V(x)=V(-x) V ( x ) = V ( − x ) E E E E E E
对于能级有简并 的情况,能量本征态并不一定就具有确定宇称,此时,可以用该定理来处理;通过定理3和定理4,可以说明定态Schrödinger方程的基本解组可全取为具有确定宇称的解。
假设 ψ ( x ) \psi(x) ψ ( x )
如果 ψ ( x ) \psi(x) ψ ( x )
如果 ψ ( x ) \psi(x) ψ ( x ) ψ ( − x ) \psi(-x) ψ ( − x ) E E E ψ ( x ) \psi(x) ψ ( x )
f ( x ) = ψ ( x ) + ψ ( − x ) , g ( x ) = ψ ( x ) − ψ ( − x ) f(x) = \psi(x) + \psi(-x),\kern 1em g(x) = \psi(x) - \psi(-x) f ( x ) = ψ ( x ) + ψ ( − x ) , g ( x ) = ψ ( x ) − ψ ( − x )
也是方程同属于能量 E E E f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) f ( − x ) = f ( x ) f(-x)=f(x) f ( − x ) = f ( x ) g ( − x ) = − g ( − x ) g(-x)=-g(-x) g ( − x ) = − g ( − x ) ψ ( x ) \psi(x) ψ ( x ) ψ ( − x ) \psi(-x) ψ ( − x )
ψ ( x ) = 1 2 [ f ( x ) + g ( x ) ] , ψ ( − x ) = 1 2 [ f ( x ) − g ( x ) ] \psi(x) = \frac12[f(x)+g(x)], \kern 1em \psi(-x) = \frac12[f(x)-g(x)] ψ ( x ) = 2 1 [ f ( x ) + g ( x )] , ψ ( − x ) = 2 1 [ f ( x ) − g ( x )]
对于阶梯方位势
V ( x ) = { V 1 , x < a V 2 , x > a V(x) = \begin{cases} V_1, & x<a \ V_2, & x>a \end{cases} V ( x ) = { V 1 , V 2 , x < a x > a
若 ( V 2 − V 1 ) (V_2-V_1) ( V 2 − V 1 ) ψ \psi ψ ψ ′ ( x ) \psi'(x) ψ ′ ( x ) ∣ V 2 − V 1 ∣ → ∞ |V_2-V_1|\to\infty ∣ V 2 − V 1 ∣ → ∞
根据定态Schrödinger方程
ψ ′ ′ ( x ) = − 2 m ℏ 2 [ E − V ( x ) ] ψ ( x ) \psi''(x) = -\frac{2m}{\hbar^2} \left[E-V(x)\right] \psi(x) ψ ′′ ( x ) = − ℏ 2 2 m [ E − V ( x ) ] ψ ( x )
在 V ( x ) V(x) V ( x ) ψ ′ ′ ( x ) \psi''(x) ψ ′′ ( x ) ψ ( x ) \psi(x) ψ ( x ) ψ ′ ( x ) \psi'(x) ψ ′ ( x )
在 V ( x ) V(x) V ( x ) V ( x ) ψ ( x ) V(x)\psi(x) V ( x ) ψ ( x ) x ∼ a x\sim a x ∼ a
lim ε → 0 + ∫ a − ε a + ε ψ ′ ′ ( x ) d x = ψ ′ ( a + 0 + ) − ψ ′ ( a − 0 + ) = − 2 m ℏ 2 lim ε → 0 + ∫ a − ε a + ε d x [ E − V ( x ) ] ψ ( x ) \lim_{\varepsilon\to0^+} \int_{a-\varepsilon}^{a+\varepsilon} \psi''(x) \mathrm{d}x = \psi'(a+0^+) - \psi'(a-0^+) = -\frac{2m}{\hbar^2} \lim_{\varepsilon\to0^+} \int_{a-\varepsilon}^{a+\varepsilon} \mathrm{d}x [E-V(x)] \psi(x) ε → 0 + lim ∫ a − ε a + ε ψ ′′ ( x ) d x = ψ ′ ( a + 0 + ) − ψ ′ ( a − 0 + ) = − ℏ 2 2 m ε → 0 + lim ∫ a − ε a + ε d x [ E − V ( x )] ψ ( x )
由于 [ E − V ( x ) ] ψ ( x ) [E-V(x)]\psi(x) [ E − V ( x )] ψ ( x ) ε → 0 + \varepsilon\to0^+ ε → 0 +
ψ ′ ( a + 0 + ) = ψ ′ ( a − 0 + ) \psi'(a+0^+) = \psi'(a-0^+) ψ ′ ( a + 0 + ) = ψ ′ ( a − 0 + )
即 ψ ′ ( x ) \psi'(x) ψ ′ ( x ) V ( x ) V(x) V ( x ) x = a x=a x = a ψ ( x ) \psi(x) ψ ( x )
若 ψ 1 ( x ) \psi_1(x) ψ 1 ( x ) ψ 2 ( x ) \psi_2(x) ψ 2 ( x ) E E E
ψ 1 ψ 2 ′ − ψ 2 ψ 1 ′ = C o n s t ( 与 x 无关 ) \psi_1\psi'_2 - \psi_2\psi'_1 = \mathrm{Const}(与x无关) ψ 1 ψ 2 ′ − ψ 2 ψ 1 ′ = Const ( 与 x 无关 )
其中 ψ 1 ψ 2 ′ − ψ 2 ψ 1 ′ \psi_1\psi'_2 - \psi_2\psi'_1 ψ 1 ψ 2 ′ − ψ 2 ψ 1 ′ ψ 1 ( x ) \psi_1(x) ψ 1 ( x ) ψ 2 ( x ) \psi_2(x) ψ 2 ( x )
W [ ψ 1 , ψ 2 ] ( x ) = ∣ ψ 1 ( x ) ψ 2 ( x ) ψ 1 ′ ( x ) ψ 2 ′ ( x ) ∣ W\psi_1,\psi_2 = \begin{vmatrix} \psi_1(x) & \psi_2(x) \ \psi'_1(x) & \psi'_2(x) \end{vmatrix} W [ ψ 1 , ψ 2 ] ( x ) = ψ 1 ( x ) ψ 1 ′ ( x ) ψ 2 ( x ) ψ 2 ′ ( x )
由定态Schrödinger方程可得
ψ 1 ′ ′ = − 2 m ℏ 2 [ E − V ( x ) ] ψ 1 ψ 2 ′ ′ = − 2 m ℏ 2 [ E − V ( x ) ] ψ 2 \psi''_1 = -\frac{2m}{\hbar^2} \left[E-V(x)\right] \psi_1 \ \kern1em \ \psi''_2 = -\frac{2m}{\hbar^2} \left[E-V(x)\right] \psi_2 ψ 1 ′′ = − ℏ 2 2 m [ E − V ( x ) ] ψ 1 ψ 2 ′′ = − ℏ 2 2 m [ E − V ( x ) ] ψ 2
ψ 1 \psi_1 ψ 1 × \times × − - − ψ 2 \psi_2 ψ 2 × \times ×
ψ 1 ψ 2 ′ ′ − ψ 2 ψ 1 ′ ′ = 0 \psi_1\psi''_2 - \psi_2\psi''_1 = 0 ψ 1 ψ 2 ′′ − ψ 2 ψ 1 ′′ = 0
即
ψ 1 ψ 2 ′ ′ − ψ 2 ψ 1 ′ ′ = ψ 1 ψ 2 ′ ′ + ψ 1 ′ ψ 2 ′ − ψ 1 ′ ψ 2 ′ − ψ 2 ψ 1 ′ ′ = ( ψ 1 ψ 2 ′ − ψ 2 ψ 1 ) ′ = 0 \psi_1\psi''_2 - \psi_2\psi''_1 = \psi_1\psi''_2 + \psi'_1\psi'_2 - \psi'_1\psi'_2 - \psi_2\psi''_1 = (\psi_1\psi'_2 - \psi_2\psi_1)' = 0 ψ 1 ψ 2 ′′ − ψ 2 ψ 1 ′′ = ψ 1 ψ 2 ′′ + ψ 1 ′ ψ 2 ′ − ψ 1 ′ ψ 2 ′ − ψ 2 ψ 1 ′′ = ( ψ 1 ψ 2 ′ − ψ 2 ψ 1 ) ′ = 0
积分,得
ψ 1 ψ 2 ′ − ψ 2 ψ 1 ′ = C o n s t ( 与 x 无关 ) \psi_1\psi'_2 - \psi_2\psi'_1 = \mathrm{Const}(与x无关) ψ 1 ψ 2 ′ − ψ 2 ψ 1 ′ = Const ( 与 x 无关 )
对于束缚态 ,当 x → ∞ x\to\infty x → ∞ ψ → 0 \psi\to0 ψ → 0 0 0 0 E E E ψ 1 \psi_1 ψ 1 ψ 2 \psi_2 ψ 2
ψ 1 ψ 2 ′ = ψ 2 ψ 1 ′ \psi_1\psi'_2 = \psi_2\psi'_1 ψ 1 ψ 2 ′ = ψ 2 ψ 1 ′
设粒子在规则势场 V ( x ) V(x) V ( x ) 束缚态 ,则必定是非简并 的。
注:对于常见的不规则势阱,在绝大多数情况下(如无限深方势阱、 δ \delta δ V ( x ) ∝ − 1 ∣ x ∣ V(x) \propto -\frac{1}{|x|} V ( x ) ∝ − ∣ x ∣ 1 2 2 2 ψ ( x ) = 0 \psi(x)=0 ψ ( x ) = 0 V ( x ) V(x) V ( x )
设 ψ 1 \psi_1 ψ 1 ψ 2 \psi_2 ψ 2 E E E
ψ 1 ψ 2 ′ = ψ 2 ψ 1 ′ \psi_1\psi'_2 = \psi_2\psi'_1 ψ 1 ψ 2 ′ = ψ 2 ψ 1 ′
在不包含 ψ 1 ( x ) \psi_1(x) ψ 1 ( x ) ψ 2 ( x ) \psi_2(x) ψ 2 ( x ) ψ 1 ψ 2 \psi_1\psi_2 ψ 1 ψ 2
ψ 2 ′ ψ 2 = ψ 1 ′ ψ 1 \frac{\psi'_2}{\psi_2} = \frac{\psi'_1}{\psi_1} ψ 2 ψ 2 ′ = ψ 1 ψ 1 ′
即
( ln ψ 1 ψ 2 ) ′ = 0 \left(\ln{\frac{\psi_1}{\psi_2}}\right)' = 0 ( ln ψ 2 ψ 1 ) ′ = 0
积分得
ln ψ 1 ψ 2 = ln C ( C 是与 x 无关的常数 ) \ln{\frac{\psi_1}{\psi_2}} = \ln C \kern 1em (C是与x无关的常数) ln ψ 2 ψ 1 = ln C ( C 是与 x 无关的常数 )
故
ψ 1 = C ψ 2 \psi_1 = C \psi_2 ψ 1 = C ψ 2
这表明 ψ 1 \psi_1 ψ 1 ψ 2 \psi_2 ψ 2
一维无限深方势阱表示为
V ( x ) = { 0 , 0 < x < a ∞ , 0 < x , x > a V(x) = \begin{cases} 0, & 0<x<a \ \infty, & 0<x,x>a \end{cases} V ( x ) = { 0 , ∞ , 0 < x < a 0 < x , x > a
在该势阱中的质量为 m m m 能量是量子化 的,即构成的能谱是离散 的,体系的能量本征值
E n = ℏ 2 π 2 n 2 2 m a 2 ( n = 1 , 2 , 3 , ⋯ ) E_n = \frac{\hbar^2\pi^2n^2}{2ma^2} \kern 1em (n=1,2,3,\cdots) E n = 2 m a 2 ℏ 2 π 2 n 2 ( n = 1 , 2 , 3 , ⋯ )
对应的能量本征函数为
ψ n ( x ) = { 2 a sin ( n π x a ) , 0 < x < a 0 , x < 0 , x > a \psi_n(x) = \begin{cases} \sqrt{\frac{2}{a}} \sin\left(\frac{n\pi x}{a}\right), & 0<x<a \ 0, & x<0,x>a \end{cases} ψ n ( x ) = { a 2 sin ( a nπ x ) , 0 , 0 < x < a x < 0 , x > a
注:若将一维无限深方势阱表示为
V ( x ) = { 0 , ∣ x ∣ < a 2 ∞ , ∣ x ∣ > a 2 V(x) = \begin{cases} 0, & |x|<\frac{a}{2} \ \infty, & |x|>\frac{a}{2} \end{cases} V ( x ) = { 0 , ∞ , ∣ x ∣ < 2 a ∣ x ∣ > 2 a
则能量本征值不变,能量本征函数变为
ψ n ( x ) = { { a 2 cos ( n π x a ) , n = 1 , 3 , 5 , ⋯ , ( 偶宇称 ) a 2 sin ( n π x a ) , n = 2 , 4 , 6 , ⋯ , ( 奇宇称 ) ∣ x ∣ < a 2 0 , ∣ x ∣ < a 2 \psi_n(x) = \begin{cases} \begin{cases} \sqrt{\frac{a}{2}} \cos\left(\frac{n\pi x}{a}\right) , & n=1,3,5,\cdots,(偶宇称) \ \sqrt{\frac{a}{2}} \sin\left(\frac{n\pi x}{a}\right) , & n=2,4,6,\cdots,(奇宇称) \end{cases} & |x|<\frac{a}{2} \ 0, & |x|<\frac{a}{2} \end{cases} ψ n ( x ) = ⎩ ⎨ ⎧ { 2 a cos ( a nπ x ) , 2 a sin ( a nπ x ) , n = 1 , 3 , 5 , ⋯ , ( 偶宇称 ) n = 2 , 4 , 6 , ⋯ , ( 奇宇称 ) 0 , ∣ x ∣ < 2 a ∣ x ∣ < 2 a
在势阱内 ( 0 < x < a ) (0<x<a) ( 0 < x < a )
d 2 d x 2 ψ ( x ) + 2 m E ℏ 2 ψ ( x ) = 0 \frac{\mathrm{d}^2}{\mathrm{d}x^2} \psi(x) + \frac{2mE}{\hbar^2} \psi(x) = 0 d x 2 d 2 ψ ( x ) + ℏ 2 2 m E ψ ( x ) = 0
其中粒子的能量 E > 0 E>0 E > 0
k = 2 m E ℏ > 0 k = \frac{\sqrt{2mE}}{\hbar} > 0 k = ℏ 2 m E > 0
则能量本征方程可表示为
d 2 d x 2 ψ ( x ) + k 2 ψ ( x ) = 0 \frac{\mathrm{d}^2}{\mathrm{d}x^2} \psi(x) + k^2 \psi(x) = 0 d x 2 d 2 ψ ( x ) + k 2 ψ ( x ) = 0
解得
ψ ( x ) = A sin ( k x + δ ) \psi(x) = A\sin(kx+\delta) ψ ( x ) = A sin ( k x + δ )
其中 A A A δ \delta δ 在阱壁上及阱外波函数为 0 0 0
ψ ( 0 ) = 0 , ψ ( a ) = 0 \psi(0) = 0, \kern 1em \psi(a) = 0 ψ ( 0 ) = 0 , ψ ( a ) = 0
由 ψ ( 0 ) = A sin ( δ ) = 0 \psi(0) = A\sin(\delta) = 0 ψ ( 0 ) = A sin ( δ ) = 0 δ = 0 \delta = 0 δ = 0 ψ ( x ) = A sin ( k x ) \psi(x) = A\sin(kx) ψ ( x ) = A sin ( k x ) ψ ( a ) = A sin ( k a ) = 0 \psi(a) = A\sin(ka) = 0 ψ ( a ) = A sin ( ka ) = 0
k a = n π ⟹ k = n π a ( n = 1 , 2 , 3 , ⋯ ) ka = n\pi \Longrightarrow k = \frac{n\pi}{a} \kern 1em (n=1,2,3,\cdots) ka = nπ ⟹ k = a nπ ( n = 1 , 2 , 3 , ⋯ )
注: n = 0 n=0 n = 0 ψ ( x ) = 0 \psi(x)=0 ψ ( x ) = 0 n n n n n n − 1 -1 − 1
k = 2 m E ℏ = n π a ⟹ E n = ℏ 2 π 2 n 2 2 m a 2 ( n = 1 , 2 , 3 , ⋯ ) k = \frac{\sqrt{2mE}}{\hbar} = \frac{n\pi}{a} \Longrightarrow E_n = \frac{\hbar^2\pi^2n^2}{2ma^2} \kern 1em (n=1,2,3,\cdots) k = ℏ 2 m E = a nπ ⟹ E n = 2 m a 2 ℏ 2 π 2 n 2 ( n = 1 , 2 , 3 , ⋯ )
则能量本征函数
ψ n ( x ) = A sin ( n π a x ) \psi_n(x) = A\sin\left(\frac{n\pi}{a}x\right) ψ n ( x ) = A sin ( a nπ x )
归一化后可得
ψ n ( x ) = 2 a sin ( n π a x ) \psi_n(x) = \sqrt{\frac{2}{a}}\sin(\frac{n\pi}{a}x) ψ n ( x ) = a 2 sin ( a nπ x )
E n = ℏ 2 π 2 n 2 2 m a 2 ∝ n 2 ( n = 1 , 2 , 3 , ⋯ ) E_n = \frac{\hbar^2\pi^2n^2}{2ma^2} \propto n^2 \kern 1em (n=1,2,3,\cdots) E n = 2 m a 2 ℏ 2 π 2 n 2 ∝ n 2 ( n = 1 , 2 , 3 , ⋯ )
能级的分布是不均匀的,能级越高,密度越小
Δ E n ≈ ℏ 2 π 2 m a 2 n , Δ E n E n = 2 n ⟶ n → ∞ 0 \Delta E_n \approx \frac{\hbar^2\pi^2}{ma^2} n, \kern 1em \frac{\Delta E_n}{E_n} = \frac{2}{n} \overset{n\to\infty}{\longrightarrow} 0 Δ E n ≈ m a 2 ℏ 2 π 2 n , E n Δ E n = n 2 ⟶ n → ∞ 0
当 n n n
最低能级不为零:
E 1 = ℏ 2 π 2 2 m a 2 > 0 E_1 = \frac{\hbar^2\pi^2}{2ma^2} > 0 E 1 = 2 m a 2 ℏ 2 π 2 > 0
这可以用不确定性关系 来解释:
粒子局限在无限深方势阱中,位置不确定度 Δ x ∼ a \Delta x \sim a Δ x ∼ a Δ p ∼ ℏ Δ x ∼ ℏ a \Delta p \sim \frac{\hbar}{\Delta x} \sim \frac{\hbar}{a} Δ p ∼ Δ x ℏ ∼ a ℏ
E ∼ p 2 2 m ∼ ( Δ p ) 2 2 m ∼ ℏ 2 2 m a 2 ≠ 0 E \sim \frac{p^2}{2m} \sim \frac{(\Delta p)^2}{2m} \sim \frac{\hbar^2}{2ma^2} \ne 0 E ∼ 2 m p 2 ∼ 2 m ( Δ p ) 2 ∼ 2 m a 2 ℏ 2 = 0
ρ n ( x ) = ∣ ψ n ( x ) ∣ 2 = 2 a sin 2 ( n π a x ) \rho_n(x) = |\psi_n(x)|^2 = \frac{2}{a}\sin^2\left(\frac{n\pi}{a}x\right) ρ n ( x ) = ∣ ψ n ( x ) ∣ 2 = a 2 sin 2 ( a nπ x )
由该图也可以看出,除端点 ( x = 0 , a ) (x=0,a) ( x = 0 , a ) 基态 (能量最低态, n = 1 n=1 n = 1 k k k k = n − 1 k=n-1 k = n − 1 k k k
一维有限深对称方势阱表示为
V ( x ) = { 0 , ∣ x ∣ < a 2 V 0 , ∣ x ∣ > a 2 V(x) = \begin{cases} 0, & |x|<\frac{a}{2} \ V_0, & |x|>\frac{a}{2} \end{cases} V ( x ) = { 0 , V 0 , ∣ x ∣ < 2 a ∣ x ∣ > 2 a
在该势阱中的质量为 m m m 束缚态 ( 0 < E < V 0 ) (0<E<V_0) ( 0 < E < V 0 )
令
k = 2 m E ℏ , β = 2 m ( V 0 − E ) ℏ k = \frac{\sqrt{2mE}}{\hbar}\ , \kern 1em \beta = \frac{\sqrt{2m(V_0-E)}}{\hbar} k = ℏ 2 m E , β = ℏ 2 m ( V 0 − E )
引入无量纲参数
ξ = k a 2 , η = β a 2 \xi = \frac{ka}{2}\ , \kern 1em \eta = \frac{\beta a}{2} ξ = 2 ka , η = 2 β a
这两个无量纲参数满足一定的方程组,使得其取值是离散的,对应的能量本征态为
E n = 2 ℏ 2 m a 2 ξ n 2 E_n = \frac{2\hbar^2}{ma^2} \xi^2_n E n = m a 2 2 ℏ 2 ξ n 2
对于偶宇称态 :
波函数形式为(可利用波函数连续性与归一化进一步求出 A A A C C C
ψ ( x ) = { C e β x , x < − a 2 A cos ( k x ) , − a 2 < x < a 2 C e − β x , x > a 2 \psi(x) = \begin{cases} C\mathrm{e}^{\beta x}, & x<-\frac{a}{2} \ A\cos(kx), & -\frac{a}{2}<x<\frac{a}{2} \ C\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} ψ ( x ) = ⎩ ⎨ ⎧ C e β x , A cos ( k x ) , C e − β x , x < − 2 a − 2 a < x < 2 a x > 2 a
无量纲参数满足方程组
{ ξ tan ξ = η ξ 2 + η 2 = m V 0 a 2 2 ℏ 2 \left{\begin{matrix} \xi\tan\xi = \eta \ \xi^2+\eta^2 = \frac{mV_0a^2}{2\hbar^2} \end{matrix}\right. { ξ tan ξ = η ξ 2 + η 2 = 2 ℏ 2 m V 0 a 2
对于奇宇称态 :
波函数形式为(可利用波函数连续性与归一化进一步求出 B B B C C C
ψ ( x ) = { C e β x , x < − a 2 B sin ( k x ) , − a 2 < x < a 2 − C e − β x , x > a 2 \psi(x) = \begin{cases} C\mathrm{e}^{\beta x}, & x<-\frac{a}{2} \ B\sin(kx), & -\frac{a}{2}<x<\frac{a}{2} \ -C\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} ψ ( x ) = ⎩ ⎨ ⎧ C e β x , B sin ( k x ) , − C e − β x , x < − 2 a − 2 a < x < 2 a x > 2 a
无量纲参数满足方程组
{ − ξ cot ξ = η ξ 2 + η 2 = m V 0 a 2 2 ℏ 2 \left{\begin{matrix} -\xi\cot\xi = \eta \ \xi^2+\eta^2 = \frac{mV_0a^2}{2\hbar^2} \end{matrix}\right. { − ξ cot ξ = η ξ 2 + η 2 = 2 ℏ 2 m V 0 a 2
先考虑势阱外的情况,能量本征方程为
d 2 d x 2 ψ ( x ) − β 2 ψ ( x ) = 0 \frac{\mathrm{d}^2}{\mathrm{d}x^2} \psi(x) - \beta^2 \psi(x) = 0 d x 2 d 2 ψ ( x ) − β 2 ψ ( x ) = 0
其中 β = 2 m ( V 0 − E ) ℏ \beta = \frac{\sqrt{2m(V_0-E)}}{\hbar} β = ℏ 2 m ( V 0 − E )
ψ ( x ) = C e β x + D e − β x \psi(x) = C\mathrm{e}^{\beta x} + D\mathrm{e}^{-\beta x} ψ ( x ) = C e β x + D e − β x
考虑束缚态边界条件,即在 x → ∞ x\to\infty x → ∞ ψ ( x ) → 0 \psi(x)\to0 ψ ( x ) → 0
ψ ( x ) = { C e β x , x < − a 2 D e − β x , x > a 2 \psi(x) = \begin{cases} C\mathrm{e}^{\beta x}, & x<-\frac{a}{2} \ D\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} ψ ( x ) = { C e β x , D e − β x , x < − 2 a x > 2 a
再考虑势阱内的情况,能量本征方程为
d 2 d x 2 ψ ( x ) + k 2 ψ ( x ) = 0 \frac{\mathrm{d}^2}{\mathrm{d}x^2} \psi(x) + k^2 \psi(x) = 0 d x 2 d 2 ψ ( x ) + k 2 ψ ( x ) = 0
其中 k = 2 m E ℏ k = \frac{\sqrt{2mE}}{\hbar} k = ℏ 2 m E
ψ ( x ) = A cos ( k x ) + B sin ( k x ) \psi(x) = A\cos(kx) + B\sin(kx) ψ ( x ) = A cos ( k x ) + B sin ( k x )
考虑到势阱具有空间反射不变性 V ( − x ) = V ( x ) V(-x)=V(x) V ( − x ) = V ( x ) cos ( k x ) \cos(kx) cos ( k x ) sin ( k x ) \sin(kx) sin ( k x )
对于偶宇称态 :
在势阱内 ( ∣ x ∣ < a 2 ) (|x|<\frac{a}{2}) ( ∣ x ∣ < 2 a ) B = 0 B=0 B = 0
ψ ( x ) = A cos ( k x ) \psi(x) = A\cos(kx) \kern 2em ψ ( x ) = A cos ( k x )
在势阱外 ( ∣ x ∣ > a 2 ) (|x|>\frac{a}{2}) ( ∣ x ∣ > 2 a ) C = D C=D C = D
ψ ( x ) = { C e β x , x < − a 2 C e − β x , x > a 2 \psi(x) = \begin{cases} C\mathrm{e}^{\beta x}, & x<-\frac{a}{2} \ C\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} ψ ( x ) = { C e β x , C e − β x , x < − 2 a x > 2 a
由定理5可知,波函数 ψ ( x ) \psi(x) ψ ( x ) ψ ′ ( x ) \psi'(x) ψ ′ ( x ) ∣ x ∣ = a 2 |x|=\frac{a}{2} ∣ x ∣ = 2 a − a 2 -\frac{a}{2} − 2 a a 2 \frac{a}{2} 2 a x = a 2 x=\frac{a}{2} x = 2 a
ψ ( x ) = { A cos ( k x ) , − a 2 < x < a 2 C e − β x , x > a 2 ψ ′ ( x ) = { − A k sin ( k x ) , − a 2 < x < a 2 − C β e − β x , x > a 2 \psi(x) = \begin{cases} A\cos(kx), & -\frac{a}{2}<x<\frac{a}{2} \ C\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} \ \kern 1em \ \psi'(x) = \begin{cases} -Ak\sin(kx), & -\frac{a}{2}<x<\frac{a}{2} \ -C\beta\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} ψ ( x ) = { A cos ( k x ) , C e − β x , − 2 a < x < 2 a x > 2 a ψ ′ ( x ) = { − A k sin ( k x ) , − Cβ e − β x , − 2 a < x < 2 a x > 2 a
则
A cos ( k a 2 ) = C e − β a 2 − A k sin ( k a 2 ) = − C β e − β a 2 A\cos(k\frac{a}{2}) = C\mathrm{e}^{-\beta\frac{a}{2}} \ \kern 1em \ -Ak\sin(k\frac{a}{2}) = -C\beta\mathrm{e}^{-\beta\frac{a}{2}} A cos ( k 2 a ) = C e − β 2 a − A k sin ( k 2 a ) = − Cβ e − β 2 a
两式相除,可消去 A , C A,C A , C
k tan ( k a 2 ) = β k\tan(k\frac{a}{2}) = \beta k tan ( k 2 a ) = β
注:也可以直接考虑 ( ln ψ ) ′ (\ln\psi)' ( ln ψ ) ′ A , C A,C A , C
引入无量纲参数
ξ = k a 2 , η = β a 2 \xi = \frac{ka}{2}\ , \kern 1em \eta = \frac{\beta a}{2} ξ = 2 ka , η = 2 β a
可得
ξ tan ξ = η \xi\tan\xi = \eta ξ tan ξ = η
同时, ξ \xi ξ η \eta η
ξ 2 + η 2 = a 2 4 ( k 2 + β 2 ) = a 2 4 [ 2 m E ℏ 2 + 2 m ( V 0 − E ) ℏ 2 ] = m V 0 a 2 2 ℏ 2 \xi^2+\eta^2 = \frac{a^2}{4}(k^2+\beta^2) = \frac{a^2}{4}\left[\frac{2mE}{\hbar^2} + \frac{2m(V_0-E)}{\hbar^2}\right] = \frac{mV_0a^2}{2\hbar^2} ξ 2 + η 2 = 4 a 2 ( k 2 + β 2 ) = 4 a 2 [ ℏ 2 2 m E + ℏ 2 2 m ( V 0 − E ) ] = 2 ℏ 2 m V 0 a 2
整理即得 ξ \xi ξ η \eta η
{ ξ tan ξ = η ξ 2 + η 2 = m V 0 a 2 2 ℏ 2 \left{\begin{matrix} \xi\tan\xi = \eta \ \xi^2+\eta^2 = \frac{mV_0a^2}{2\hbar^2} \end{matrix}\right. { ξ tan ξ = η ξ 2 + η 2 = 2 ℏ 2 m V 0 a 2
对于奇宇称态 :
在势阱内 ( ∣ x ∣ < a 2 ) (|x|<\frac{a}{2}) ( ∣ x ∣ < 2 a ) A = 0 A=0 A = 0
ψ ( x ) = B sin ( k x ) \psi(x) = B\sin(kx) \kern 2em ψ ( x ) = B sin ( k x )
在势阱外 ( ∣ x ∣ > a 2 ) (|x|>\frac{a}{2}) ( ∣ x ∣ > 2 a ) C = − D C=-D C = − D
ψ ( x ) = { C e β x , x < − a 2 − C e − β x , x > a 2 \psi(x) = \begin{cases} C\mathrm{e}^{\beta x}, & x<-\frac{a}{2} \ -C\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} ψ ( x ) = { C e β x , − C e − β x , x < − 2 a x > 2 a
波函数 ψ ( x ) \psi(x) ψ ( x ) ψ ′ ( x ) \psi'(x) ψ ′ ( x ) x = a 2 x=\frac{a}{2} x = 2 a
ψ ( x ) = { B sin ( k x ) , − a 2 < x < a 2 − C e − β x , x > a 2 ψ ′ ( x ) = { B k cos ( k x ) , − a 2 < x < a 2 C β e − β x , x > a 2 \psi(x) = \begin{cases} B\sin(kx), & -\frac{a}{2}<x<\frac{a}{2} \ -C\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} \ \kern 1em \ \psi'(x) = \begin{cases} Bk\cos(kx), & -\frac{a}{2}<x<\frac{a}{2} \ C\beta\mathrm{e}^{-\beta x}, & x>\frac{a}{2} \end{cases} ψ ( x ) = { B sin ( k x ) , − C e − β x , − 2 a < x < 2 a x > 2 a ψ ′ ( x ) = { B k cos ( k x ) , Cβ e − β x , − 2 a < x < 2 a x > 2 a
则
B sin ( k a 2 ) = − C e − β a 2 B k cos ( k a 2 ) = C β e − β a 2 B\sin(k\frac{a}{2}) = -C\mathrm{e}^{-\beta\frac{a}{2}} \ \kern 1em \ Bk\cos(k\frac{a}{2}) = C\beta\mathrm{e}^{-\beta\frac{a}{2}} B sin ( k 2 a ) = − C e − β 2 a B k cos ( k 2 a ) = Cβ e − β 2 a
两式相除,可消去 B , C B,C B , C
− k cot ( k a 2 ) = β -k\cot(k\frac{a}{2}) = \beta − k cot ( k 2 a ) = β
引入无量纲参数
ξ = k a 2 , η = β a 2 \xi = \frac{ka}{2}\ , \kern 1em \eta = \frac{\beta a}{2} ξ = 2 ka , η = 2 β a
可得
− ξ cot ξ = η -\xi\cot\xi = \eta − ξ cot ξ = η
同时, ξ \xi ξ η \eta η
ξ 2 + η 2 = m V 0 a 2 2 ℏ 2 \xi^2+\eta^2 =\frac{mV_0a^2}{2\hbar^2} ξ 2 + η 2 = 2 ℏ 2 m V 0 a 2
整理即得 ξ \xi ξ η \eta η
{ − ξ cot ξ = η ξ 2 + η 2 = m V 0 a 2 2 ℏ 2 \left{\begin{matrix} -\xi\cot\xi = \eta \ \xi^2+\eta^2 = \frac{mV_0a^2}{2\hbar^2} \end{matrix}\right. { − ξ cot ξ = η ξ 2 + η 2 = 2 ℏ 2 m V 0 a 2
对于 ξ \xi ξ η \eta η m V 0 a 2 2 ℏ 2 \sqrt{\frac{mV_0a^2}{2\hbar^2}} 2 ℏ 2 m V 0 a 2 偶宇称态 ,图为:
对于奇宇称态 ,图为:
注:实际上对于确定的 m , a , V 0 m,a,V_0 m , a , V 0
在一维有限深对称方势阱问题中,无论势阱多浅或多窄(即无论 V 0 a 2 V_0a^2 V 0 a 2
而对于奇宇称态的方程组,只有当
ξ 2 + η 2 = m V 0 a 2 2 ℏ 2 ≥ ( π 2 ) 2 \xi^2+\eta^2 = \frac{mV_0a^2}{2\hbar^2} \ge \left(\frac{\pi}{2}\right)^2 ξ 2 + η 2 = 2 ℏ 2 m V 0 a 2 ≥ ( 2 π ) 2
即
V 0 a 2 ≥ π 2 ℏ 2 2 m V_0a^2 \ge \frac{\pi^2\hbar^2}{2m} V 0 a 2 ≥ 2 m π 2 ℏ 2
方程组才会有解,即才可能出现最低的奇宇称能级。
随着 V 0 a 2 V_0a^2 V 0 a 2 m V 0 a 2 2 ℏ 2 \sqrt{\frac{mV_0a^2}{2\hbar^2}} 2 ℏ 2 m V 0 a 2 π 2 \frac{\pi}{2} 2 π
N = 1 + ⌊ a ℏ π 2 m V 0 ⌋ N = 1+\left\lfloor\frac{a}{\hbar\pi}\sqrt{2mV_0}\right\rfloor N = 1 + ⌊ ℏ π a 2 m V 0 ⌋
ξ = k a 2 = a 2 2 m E ℏ ⟹ E n = 2 ℏ 2 m a 2 ξ n 2 \xi = \frac{ka}{2} = \frac{a}{2}\frac{\sqrt{2mE}}{\hbar} \Longrightarrow E_n = \frac{2\hbar^2}{ma^2} \xi_n^2 ξ = 2 ka = 2 a ℏ 2 m E ⟹ E n = m a 2 2 ℏ 2 ξ n 2
由上图可得
0 < ξ 1 < π 2 < ξ 2 < π < ⋯ < π 2 ( n − 1 ) < ξ n < π 2 n < ⋯ 0<\xi_1<\frac{\pi}{2}<\xi_2<\pi<\cdots<\frac{\pi}{2}(n-1)<\xi_n<\frac{\pi}{2}n<\cdots 0 < ξ 1 < 2 π < ξ 2 < π < ⋯ < 2 π ( n − 1 ) < ξ n < 2 π n < ⋯
故有限深方势阱每个能级都比无限深方势阱的相应能级低一些:
E n = 2 ℏ 2 m a 2 ξ n 2 < π 2 ℏ 2 2 m a 2 n 2 E_n = \frac{2\hbar^2}{ma^2} \xi_n^2 < \frac{\pi^2\hbar^2}{2ma^2} n^2 E n = m a 2 2 ℏ 2 ξ n 2 < 2 m a 2 π 2 ℏ 2 n 2
当 V 0 → + ∞ V_0\to+\infty V 0 → + ∞ ξ n → π 2 n \xi_n\to\frac{\pi}{2}n ξ n → 2 π n E n → π 2 ℏ 2 2 m a 2 n 2 E_n\to\frac{\pi^2\hbar^2}{2ma^2}n^2 E n → 2 m a 2 π 2 ℏ 2 n 2
取谐振子的平衡位置为坐标原点,并选原点为势能的零点,则以为谐振子的势能可以表示为
V ( x ) = 1 2 m ω 2 x 2 V(x) = \frac12m\omega^2x^2 V ( x ) = 2 1 m ω 2 x 2
其中 m m m ω \omega ω 束缚态 ,谐振子的能量本征值 为
E n = ( n + 1 2 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ ) E_n = (n+\frac12)\hbar\omega \kern 2em (n=0,1,2,\cdots) E n = ( n + 2 1 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ )
正交归一化的能量本征函数 为
ψ n ( x ) = A n e − α 2 x 2 2 H n ( α x ) \psi_n(x) = A_n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) ψ n ( x ) = A n e − 2 α 2 x 2 H n ( αx )
其中 α = m ω ℏ \alpha=\sqrt{\frac{m\omega}{\hbar}} α = ℏ mω H n ( x ) \mathrm{H}_n(x) H n ( x )
A n = α π 2 n ⋅ n ! A_n = \sqrt{\frac{\alpha}{\sqrt{\pi}2^n\cdot n!}} A n = π 2 n ⋅ n ! α
一维谐振子的能量本征方程为
[ − ℏ 2 2 m d 2 d x 2 + 1 2 m ω 2 x 2 ] ψ ( x ) = E ψ ( x ) \left[-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}+\frac12m\omega^2x^2\right] \psi(x) = E \psi(x) [ − 2 m ℏ 2 d x 2 d 2 + 2 1 m ω 2 x 2 ] ψ ( x ) = E ψ ( x )
令 α = m ω ℏ \alpha=\sqrt{\frac{m\omega}{\hbar}} α = ℏ mω
ξ = α x , λ = E 1 2 ℏ ω \xi = \alpha x , \kern 1em \lambda = \frac{E}{\frac12\hbar\omega} ξ = αx , λ = 2 1 ℏ ω E
则方程可整理为
d 2 d ξ 2 ψ + ( λ − ξ 2 ) ψ = 0 \frac{\mathrm{d}^2}{\mathrm{d}\xi^2} \psi + (\lambda-\xi^2) \psi = 0 d ξ 2 d 2 ψ + ( λ − ξ 2 ) ψ = 0
设解的形式为
ψ = e − ξ 2 2 u ( ξ ) \psi = \mathrm{e}^{-\frac{\xi^2}{2}} u(\xi) ψ = e − 2 ξ 2 u ( ξ )
之所以这么设,可以按如下方式考虑:当 ξ → ∞ \xi\to\infty ξ → ∞ d 2 d ξ 2 ψ − ξ 2 ψ = 0 \frac{\mathrm{d}^2}{\mathrm{d}\xi^2} \psi -\xi^2 \psi = 0 d ξ 2 d 2 ψ − ξ 2 ψ = 0 ψ = e ± ξ 2 2 \psi = \mathrm{e}^{\pm\frac{\xi^2}{2}} ψ = e ± 2 ξ 2 ψ ′ = ± ξ e ± ξ 2 2 \psi' = \pm\xi \mathrm{e}^{\pm\frac{\xi^2}{2}} ψ ′ = ± ξ e ± 2 ξ 2 ψ ′ ′ = ( ξ 2 ± 1 ) e ± ξ 2 2 ≈ ξ 2 e ± ξ 2 2 = ξ 2 ψ \psi'' = (\xi^2\pm1) \mathrm{e}^{\pm\frac{\xi^2}{2}} \approx \xi^2 \mathrm{e}^{\pm\frac{\xi^2}{2}} = \xi^2\psi ψ ′′ = ( ξ 2 ± 1 ) e ± 2 ξ 2 ≈ ξ 2 e ± 2 ξ 2 = ξ 2 ψ ψ ∼ e ± ξ 2 2 \psi \sim \mathrm{e}^{\pm\frac{\xi^2}{2}} ψ ∼ e ± 2 ξ 2 ξ → ∞ \xi\to\infty ξ → ∞ ψ → 0 \psi\to0 ψ → 0 ψ ∼ e ξ 2 2 \psi \sim \mathrm{e}^{\frac{\xi^2}{2}} ψ ∼ e 2 ξ 2
将上述解的形式代入原方程,可得到 u ( ξ ) u(\xi) u ( ξ )
d 2 d ξ 2 u + 2 ξ d d ξ u + ( λ − 1 ) u = 0 \frac{\mathrm{d}^2}{\mathrm{d}\xi^2} u + 2\xi \frac{\mathrm{d}}{\mathrm{d}\xi} u + (\lambda-1) u = 0 d ξ 2 d 2 u + 2 ξ d ξ d u + ( λ − 1 ) u = 0
此即Hermite方程 ,可以通过级数解法求解:在 ξ = 0 \xi=0 ξ = 0
u ( ξ ) = ∑ k = 0 + ∞ c k ξ k u(\xi) = \sum_{k=0}^{+\infty} c_k \xi^k u ( ξ ) = k = 0 ∑ + ∞ c k ξ k
代入Hermite方程,比较同幂项的系数,可得
c k + 2 = 2 k − ( λ − 1 ) ( k + 2 ) ( k + 1 ) c k ( k = 0 , 1 , 2 , ⋯ ) c_{k+2} = \frac{2k-(\lambda-1)}{(k+2)(k+1)} c_k \kern 2em (k=0,1,2,\cdots) c k + 2 = ( k + 2 ) ( k + 1 ) 2 k − ( λ − 1 ) c k ( k = 0 , 1 , 2 , ⋯ )
故所有的偶次项系数都可以用 c 0 c_0 c 0 c 1 c_1 c 1 c 0 c_0 c 0 c 1 c_1 c 1
u 1 ( ξ ) = ∑ m = 0 + ∞ c 2 m ξ 2 m = c 0 + c 2 ξ 2 + c 4 ξ 4 + ⋯ u 2 ( ξ ) = ∑ m = 0 + ∞ c 2 m + 1 ξ 2 m + 1 = c 1 ξ + c 3 ξ 3 + c 5 ξ 5 + ⋯ u_1(\xi) = \sum_{m=0}^{+\infty} c_{2m} \xi^{2m} = c_0 + c_2\xi^2 + c_4\xi^4 + \cdots \ \kern 1em \ u_2(\xi) = \sum_{m=0}^{+\infty} c_{2m+1} \xi^{2m+1} = c_1\xi + c_3\xi^3 + c_5\xi^5 + \cdots u 1 ( ξ ) = m = 0 ∑ + ∞ c 2 m ξ 2 m = c 0 + c 2 ξ 2 + c 4 ξ 4 + ⋯ u 2 ( ξ ) = m = 0 ∑ + ∞ c 2 m + 1 ξ 2 m + 1 = c 1 ξ + c 3 ξ 3 + c 5 ξ 5 + ⋯
考虑当 ξ → ∞ \xi\to\infty ξ → ∞ k → + ∞ k\to+\infty k → + ∞
c k + 2 c k = 2 k − ( λ − 1 ) ( k + 2 ) ( k + 1 ) → 2 k \frac{c_{k+2}}{c_k} = \frac{2k-(\lambda-1)}{(k+2)(k+1)} \to \frac{2}{k} c k c k + 2 = ( k + 2 ) ( k + 1 ) 2 k − ( λ − 1 ) → k 2
对于偶数的情况,即 k = 2 m k=2m k = 2 m c 2 m + 2 / c 2 m ∼ 1 / m c_{2m+2}/c_{2m} \sim 1/m c 2 m + 2 / c 2 m ∼ 1/ m e ξ 2 \mathrm{e}^{\xi^2} e ξ 2
e ξ 2 = ∑ m = 0 + ∞ ξ 2 m m ! \mathrm{e}^{\xi^2} = \sum_{m=0}^{+\infty} \frac{\xi^{2m}}{m!} e ξ 2 = m = 0 ∑ + ∞ m ! ξ 2 m
相邻两项的系数比相同,因此,
u 1 ( ξ ) ∼ e ξ 2 u_1(\xi) \sim \mathrm{e}^{\xi^2} u 1 ( ξ ) ∼ e ξ 2
同理可得
u 2 ( ξ ) ∼ ξ e ξ 2 u_2(\xi) \sim \xi\mathrm{e}^{\xi^2} u 2 ( ξ ) ∼ ξ e ξ 2
代回到波函数可得
ψ 1 = e − ξ 2 2 u 1 ( ξ ) ∼ e ξ 2 2 ψ 2 = e − ξ 2 2 u 2 ( ξ ) ∼ ξ e ξ 2 2 \psi_1 = \mathrm{e}^{-\frac{\xi^2}{2}} u_1(\xi) \sim \mathrm{e}^{\frac{\xi^2}{2}} \ \kern 1em \ \psi_2 = \mathrm{e}^{-\frac{\xi^2}{2}} u_2(\xi) \sim \xi\mathrm{e}^{\frac{\xi^2}{2}} ψ 1 = e − 2 ξ 2 u 1 ( ξ ) ∼ e 2 ξ 2 ψ 2 = e − 2 ξ 2 u 2 ( ξ ) ∼ ξ e 2 ξ 2
这不满足束缚态的边界条件(当 ξ → ∞ \xi\to\infty ξ → ∞ ψ → 0 \psi\to0 ψ → 0 u 1 u_1 u 1 u 2 u_2 u 2 中断为多项式 ,也就是要找到合适的 λ \lambda λ k ∈ N k\in\mathbb{N} k ∈ N 2 k − ( λ − 1 ) ( k + 2 ) ( k + 1 ) = 0 \frac{2k-(\lambda-1)}{(k+2)(k+1)} = 0 ( k + 2 ) ( k + 1 ) 2 k − ( λ − 1 ) = 0
λ − 1 = 2 n ( n = 0 , 1 , 2 , ⋯ ) \lambda-1 = 2n \kern 2em (n=0,1,2,\cdots) λ − 1 = 2 n ( n = 0 , 1 , 2 , ⋯ )
时,级数将中断一个多项式( c n + 2 = c n + 4 = c n + 6 = ⋯ = 0 c_{n+2} = c_{n+4} = c_{n+6} = \cdots = 0 c n + 2 = c n + 4 = c n + 6 = ⋯ = 0 n n n u 1 u_1 u 1 H n ( ξ ) \mathrm{H}_n(\xi) H n ( ξ ) u 2 u_2 u 2 n n n u 2 u_2 u 2 H n ( ξ ) \mathrm{H}_n(\xi) H n ( ξ ) u 1 u_1 u 1 Hermite多项式 表示为
H n ( ξ ) = ( − 1 ) n e ξ 2 d n d ξ n e − ξ 2 = ( 2 ξ ) n + n ( n − 1 ) ( 2 ξ ) n − 2 + ⋯ + ( − 1 ) ⌊ n 2 ⌋ n ! ⌊ n 2 ⌋ ! ( 2 ξ ) n − 2 ⌊ n 2 ⌋ \mathrm{H}_n(\xi) = (-1)^n \mathrm{e}^{\xi^2} \frac{\mathrm{d}^n }{\mathrm{d}\xi^n} \mathrm{e}^{-\xi^2} \ = (2\xi)^n + n(n-1)(2\xi)^{n-2} + \cdots + (-1)^{\left\lfloor \frac{n}{2} \right\rfloor} \frac{n!}{\left\lfloor \frac{n}{2} \right\rfloor!} (2\xi)^{n-2\left\lfloor \frac{n}{2} \right\rfloor} H n ( ξ ) = ( − 1 ) n e ξ 2 d ξ n d n e − ξ 2 = ( 2 ξ ) n + n ( n − 1 ) ( 2 ξ ) n − 2 + ⋯ + ( − 1 ) ⌊ 2 n ⌋ ⌊ 2 n ⌋ ! n ! ( 2 ξ ) n − 2 ⌊ 2 n ⌋
例如
H 0 ( ξ ) = 1 H 1 ( ξ ) = 2 ξ H 2 ( ξ ) = 4 ξ 2 − 2 \mathrm{H}_0(\xi) = 1 \ \mathrm{H}_1(\xi) = 2\xi \ \mathrm{H}_2(\xi) = 4\xi^2 -2 H 0 ( ξ ) = 1 H 1 ( ξ ) = 2 ξ H 2 ( ξ ) = 4 ξ 2 − 2
Hermite多项式的带权正交归一性表示为
∫ − ∞ + ∞ H m ( ξ ) H n ( ξ ) e − ξ 2 d ξ = π 2 n ⋅ n ! δ m n \int_{-\infty}^{+\infty} \mathrm{H}_m(\xi) \mathrm{H}n(\xi) \mathrm{e}^{-\xi^2} \mathrm{d}\xi = \sqrt{\pi} 2^n \cdot n! \delta {mn} ∫ − ∞ + ∞ H m ( ξ ) H n ( ξ ) e − ξ 2 d ξ = π 2 n ⋅ n ! δ mn
根据 λ \lambda λ 能量本征值
λ = E 1 2 ℏ ω = 2 n + 1 ⟹ E n = ( n + 1 2 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ ) \lambda = \frac{E}{\frac12\hbar\omega} = 2n+1 \Longrightarrow E_n = (n+\frac12)\hbar\omega \kern 2em (n=0,1,2,\cdots) λ = 2 1 ℏ ω E = 2 n + 1 ⟹ E n = ( n + 2 1 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ )
借助Hermite多项式,并把 ξ = α x \xi=\alpha x ξ = αx 能量本征函数
ψ n ∝ e − ξ 2 2 H n ( ξ ) ⟹ ψ n ( x ) = A n e − α 2 x 2 2 H n ( α x ) \psi_n \propto \mathrm{e}^{-\frac{\xi^2}{2}} \mathrm{H}_n(\xi) \Longrightarrow \psi_n(x) = A_n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) ψ n ∝ e − 2 ξ 2 H n ( ξ ) ⟹ ψ n ( x ) = A n e − 2 α 2 x 2 H n ( αx )
根据Hermite多项式的带权正交归一性,
( ψ m , ψ n ) = A m A n ∫ − ∞ + ∞ H m ( ξ ) H n ( ξ ) e − ξ 2 d ξ = A m A n π 2 n ⋅ n ! δ m n (\psi_m,\psi_n) = A_mA_n \int_{-\infty}^{+\infty} \mathrm{H}_m(\xi) \mathrm{H}n(\xi) \mathrm{e}^{-\xi^2} \mathrm{d}\xi = A_mA_n\sqrt{\pi} 2^n \cdot n! \delta {mn} ( ψ m , ψ n ) = A m A n ∫ − ∞ + ∞ H m ( ξ ) H n ( ξ ) e − ξ 2 d ξ = A m A n π 2 n ⋅ n ! δ mn
可得归一化系数
A n = α π 2 n ⋅ n ! A_n = \sqrt{\frac{\alpha}{\sqrt{\pi}2^n\cdot n!}} A n = π 2 n ⋅ n ! α
这样波函数就满足了正交归一化条件
( ψ m , ψ n ) = δ m n (\psi_m,\psi_n) = \delta_{mn} ( ψ m , ψ n ) = δ mn
E n = ( n + 1 2 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ ) E_n = (n+\frac12)\hbar\omega \kern 2em (n=0,1,2,\cdots) E n = ( n + 2 1 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ )
一维谐振子的能量是均匀分布 的,相邻的两条能级间距为 E n + 1 − E n = ℏ ω E_{n+1} - E_n = \hbar\omega E n + 1 − E n = ℏ ω
最低的三条能级上的谐振子波函数如下:
ψ 0 ( x ) = α π 1 4 e − α 2 x 2 2 ψ 1 ( x ) = 2 α π 1 4 α x e − α 2 x 2 2 ψ 2 ( x ) = 1 π 1 4 α 2 ( 2 α 2 x 2 − 1 ) e − α 2 x 2 2 \psi_0(x) = \frac{\sqrt{\alpha}}{\pi^{\frac{1}{4}}} \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \ \kern 1em \ \psi_1(x) = \frac{\sqrt{2\alpha}}{\pi^{\frac{1}{4}}} \alpha x\ \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \ \kern 1em \ \psi_2(x) = \frac{1}{\pi^{\frac{1}{4}}} \sqrt{\frac{\alpha}{2}} (2\alpha^2x^2-1) \mathrm{e}^{-\frac{\alpha^2x^2}{2}} ψ 0 ( x ) = π 4 1 α e − 2 α 2 x 2 ψ 1 ( x ) = π 4 1 2 α αx e − 2 α 2 x 2 ψ 2 ( x ) = π 4 1 1 2 α ( 2 α 2 x 2 − 1 ) e − 2 α 2 x 2
其中 ψ n ( x ) \psi_n(x) ψ n ( x ) n n n
由于一维谐振子势具有空间反射不变性( V ( − x ) = V ( x ) V(-x)=V(x) V ( − x ) = V ( x ) ψ n ( x ) \psi_n(x) ψ n ( x )
ψ n ( − x ) = ( − 1 ) n ψ n ( x ) \psi_n(-x) = (-1)^n \psi_n(x) ψ n ( − x ) = ( − 1 ) n ψ n ( x )
能级的宇称偶奇相间,基态是偶宇称。
一维谐振子基态能量为
E 0 = 1 2 ℏ ω E_0 = \frac12 \hbar\omega E 0 = 2 1 ℏ ω
其并不为零(可以用不确定性关系解释),称为零点能 。
处于基态的谐振子在空间的概率分布为
∣ ψ 0 ( x ) ∣ 2 = α π e − α 2 x 2 |\psi_0(x)|^2 = \frac{\alpha}{\sqrt{\pi}} \mathrm{e}^{-\alpha^2x^2} ∣ ψ 0 ( x ) ∣ 2 = π α e − α 2 x 2
这是一个Gauss型分布,在原点 ( x = 0 ) (x=0) ( x = 0 )
对于一维谐振子,其Hamilton算符
H ^ = − ℏ 2 2 m ∂ 2 ∂ x 2 + 1 2 m ω 2 x 2 \hat{H} = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \frac12m\omega^2x^2 H ^ = − 2 m ℏ 2 ∂ x 2 ∂ 2 + 2 1 m ω 2 x 2
二维谐振子的势能可以表示为
V ( x , y ) = 1 2 m ω 2 r 2 = 1 2 m ω 2 ( x 2 + y 2 ) V(x,y) = \frac12m\omega^2r^2 = \frac12m\omega^2(x^2+y^2) V ( x , y ) = 2 1 m ω 2 r 2 = 2 1 m ω 2 ( x 2 + y 2 )
其Hamilton算符可以表示为
H ^ = − ℏ 2 2 m ( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 ) + 1 2 m ω 2 ( x 2 + y 2 ) = H ^ x + H ^ y \hat{H} = -\frac{\hbar^2}{2m} \left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) + \frac12m\omega^2(x^2+y^2) = \hat{H}_x + \hat{H}_y H ^ = − 2 m ℏ 2 ( ∂ x 2 ∂ 2 + ∂ y 2 ∂ 2 ) + 2 1 m ω 2 ( x 2 + y 2 ) = H ^ x + H ^ y
对于二维谐振子的能量本征方程
H ^ ψ ( x , y ) = E ψ ( x , y ) \hat{H} \psi(x,y) = E \psi(x,y) H ^ ψ ( x , y ) = E ψ ( x , y )
由于 x , y x,y x , y ψ ( x , y ) = ψ x ( x ) ψ y ( y ) \psi(x,y)=\psi_x(x)\psi_y(y) ψ ( x , y ) = ψ x ( x ) ψ y ( y )
( H ^ x + H ^ y ) ψ x ψ y = E ψ x ψ y ⇓ ψ y H ^ x ψ x + ψ x H ^ y ψ y = E ψ x ψ y ⇓ H ^ x ψ x ψ x + H ^ y ψ y ψ y = E (\hat{H}_x + \hat{H}_y)\psi_x\psi_y = E\psi_x\psi_y \ \Downarrow \ \psi_y\hat{H}_x\psi_x + \psi_x\hat{H}_y\psi_y = E\psi_x\psi_y \ \Downarrow \ \frac{\hat{H}_x\psi_x}{\psi_x} + \frac{\hat{H}_y\psi_y}{\psi_y} = E ( H ^ x + H ^ y ) ψ x ψ y = E ψ x ψ y ⇓ ψ y H ^ x ψ x + ψ x H ^ y ψ y = E ψ x ψ y ⇓ ψ x H ^ x ψ x + ψ y H ^ y ψ y = E
这样,能量本征方程就可以分离为 x , y x,y x , y
H ^ x ψ x = E x ψ x , H ^ y ψ y = E y ψ y \hat{H}_x\psi_x = E_x\psi_x\ , \kern 1em \hat{H}_y\psi_y = E_y\psi_y H ^ x ψ x = E x ψ x , H ^ y ψ y = E y ψ y
则二维谐振子的能量本征函数 为
ψ n x n y ( x , y ) = ψ n x ( x ) ψ n y ( y ) ( n x , n y = 0 , 1 , 2 , ⋯ ) \psi_{n_xn_y}(x,y) = \psi_{n_x}(x) \psi_{n_y}(y) \kern 2em (n_x,n_y=0,1,2,\cdots) ψ n x n y ( x , y ) = ψ n x ( x ) ψ n y ( y ) ( n x , n y = 0 , 1 , 2 , ⋯ )
其中 ψ n x , ψ n y \psi_{n_x},\psi_{n_y} ψ n x , ψ n y ψ n \psi_n ψ n
二维谐振子的能量本征值 为
E n x n y = E n x + E n y = ( 1 2 + n x ) ℏ ω + ( 1 2 + n y ) ℏ ω = ( 1 + n x + n y ) ℏ ω ( n x , n y = 0 , 1 , 2 , ⋯ ) E_{n_xn_y} = E_{n_x} + E_{n_y} = (\frac12+n_x)\hbar\omega + (\frac12+n_y)\hbar\omega = (1+n_x+n_y)\hbar\omega \kern 2em (n_x,n_y=0,1,2,\cdots) E n x n y = E n x + E n y = ( 2 1 + n x ) ℏ ω + ( 2 1 + n y ) ℏ ω = ( 1 + n x + n y ) ℏ ω ( n x , n y = 0 , 1 , 2 , ⋯ )
其中 E n x , E n y E_{n_x},E_{n_y} E n x , E n y E n E_n E n N = n x + n y N=n_x+n_y N = n x + n y
E n x n y = ( 1 + N ) ℏ ω ( N = 0 , 1 , 2 , ⋯ ) E_{n_xn_y} = (1+N)\hbar\omega \kern 2em (N=0,1,2,\cdots) E n x n y = ( 1 + N ) ℏ ω ( N = 0 , 1 , 2 , ⋯ )
对于给定的 N N N ( n x , n y ) (n_x,n_y) ( n x , n y ) N + 1 N+1 N + 1 ( 0 , N ) , ( 1 , N − 1 ) , ⋯ , ( N , 0 ) (0,N),(1,N-1),\cdots,(N,0) ( 0 , N ) , ( 1 , N − 1 ) , ⋯ , ( N , 0 ) 简并度
f N = N + 1 f_N = N+1 f N = N + 1
三维谐振子的结论与二维谐振子类似,能量本征函数 为
ψ n x n y n y ( x , y , z ) = ψ n x ( x ) ψ n y ( y ) ψ n z ( z ) ( n x , n y , n z = 0 , 1 , 2 , ⋯ ) \psi_{n_xn_yn_y}(x,y,z) = \psi_{n_x}(x) \psi_{n_y}(y) \psi_{n_z}(z) \kern 2em (n_x,n_y,n_z=0,1,2,\cdots) ψ n x n y n y ( x , y , z ) = ψ n x ( x ) ψ n y ( y ) ψ n z ( z ) ( n x , n y , n z = 0 , 1 , 2 , ⋯ )
能量本征值 为
E n x n y n y = E n x + E n y + E n z = ( 1 2 + n x ) ℏ ω + ( 1 2 + n y ) ℏ ω + ( 1 2 + n z ) ℏ ω = ( 3 2 + n x + n y + n z ) ℏ ω ( n x , n y , n y = 0 , 1 , 2 , ⋯ ) E_{n_xn_yn_y} = E_{n_x} + E_{n_y} + E_{n_z} = (\frac12+n_x)\hbar\omega + (\frac12+n_y)\hbar\omega + (\frac12+n_z)\hbar\omega \ = (\frac32+n_x+n_y+n_z)\hbar\omega\kern 2em (n_x,n_y,n_y=0,1,2,\cdots) E n x n y n y = E n x + E n y + E n z = ( 2 1 + n x ) ℏ ω + ( 2 1 + n y ) ℏ ω + ( 2 1 + n z ) ℏ ω = ( 2 3 + n x + n y + n z ) ℏ ω ( n x , n y , n y = 0 , 1 , 2 , ⋯ )
记 N = n x + n y + n z N=n_x+n_y+n_z N = n x + n y + n z
E n x n y n z = ( 3 2 + N ) ℏ ω ( N = 0 , 1 , 2 , ⋯ ) E_{n_xn_yn_z} = (\frac32+N)\hbar\omega \kern 2em (N=0,1,2,\cdots) E n x n y n z = ( 2 3 + N ) ℏ ω ( N = 0 , 1 , 2 , ⋯ )
对于给定的 N N N ( n x , n y , n z ) (n_x,n_y,n_z) ( n x , n y , n z )
∑ n x = 0 N ( N + 1 − n x ) = ∑ k = 1 N + 1 k = 1 2 ( N + 1 ) ( N + 2 ) \sum_{n_x=0}^{N} (N+1-n_x) = \sum_{k=1}^{N+1} k = \frac12(N+1)(N+2) n x = 0 ∑ N ( N + 1 − n x ) = k = 1 ∑ N + 1 k = 2 1 ( N + 1 ) ( N + 2 )
故能级简并度
f N = 1 2 ( N + 1 ) ( N + 2 ) f_N = \frac12(N+1)(N+2) f N = 2 1 ( N + 1 ) ( N + 2 )
δ \delta δ
V ( x ) = − γ δ ( x ) ( γ > 0 ) V(x) = -\gamma \delta(x) \kern 2em (\gamma > 0) V ( x ) = − γ δ ( x ) ( γ > 0 )
质量为 m m m δ \delta δ x ≠ 0 x\ne0 x = 0 V ( x ) = 0 V(x)=0 V ( x ) = 0 E > 0 E>0 E > 0 E E E E < 0 E<0 E < 0 束缚 能量本征态, E E E E < 0 E<0 E < 0
能量本征方程为
ψ ′ ′ ( x ) = − 2 m ℏ 2 [ E + γ δ ( x ) ] ψ ( x ) \psi''(x) = -\frac{2m}{\hbar^2} \left[E+\gamma\delta(x)\right] \psi(x) ψ ′′ ( x ) = − ℏ 2 2 m [ E + γ δ ( x ) ] ψ ( x )
左右两边同时积分可以得到 δ \delta δ ψ ′ \psi' ψ ′ 跃变条件 :
lim ε → 0 + ∫ − ε ε ψ ′ ′ ( x ) d x = lim ε → 0 + ∫ − ε ε − 2 m ℏ 2 [ E + γ δ ( x ) ] ψ ( x ) d x ⇓ ψ ′ ( 0 + ) − ψ ′ ( 0 − ) = − 2 m γ ℏ 2 ψ ( 0 ) \lim_{\varepsilon\to0^+} \int_{-\varepsilon}^{\varepsilon} \psi''(x) \mathrm{d}x = \lim_{\varepsilon\to0^+} \int_{-\varepsilon}^{\varepsilon} -\frac{2m}{\hbar^2} \left[E+\gamma\delta(x)\right] \psi(x) \mathrm{d}x \ \Downarrow \ \psi'(0^+) - \psi'(0^-) = -\frac{2m\gamma}{\hbar^2} \psi(0) ε → 0 + lim ∫ − ε ε ψ ′′ ( x ) d x = ε → 0 + lim ∫ − ε ε − ℏ 2 2 m [ E + γ δ ( x ) ] ψ ( x ) d x ⇓ ψ ′ ( 0 + ) − ψ ′ ( 0 − ) = − ℏ 2 2 mγ ψ ( 0 )
令
β = − 2 m E ℏ > 0 \beta = \frac{\sqrt{-2mE}}{\hbar} > 0 β = ℏ − 2 m E > 0
则在 x ≠ 0 x\ne0 x = 0
ψ ′ ′ ( x ) − β 2 ψ ( x ) = 0 \psi''(x) - \beta^2\psi(x) = 0 ψ ′′ ( x ) − β 2 ψ ( x ) = 0
解得
ψ ( x ) = A e β x + B e − β x \psi(x) = A\mathrm{e}^{\beta x} + B\mathrm{e}^{-\beta x} ψ ( x ) = A e β x + B e − β x
考虑到束缚态边界条件,即在 x → ∞ x\to\infty x → ∞ ψ ( x ) → 0 \psi(x)\to0 ψ ( x ) → 0
ψ ( x ) = { A e β x , x < 0 B e − β x , x > 0 \psi(x) = \begin{cases} A\mathrm{e}^{\beta x}, & x<0 \ B\mathrm{e}^{-\beta x}, & x>0 \end{cases} ψ ( x ) = { A e β x , B e − β x , x < 0 x > 0
考虑到势阱具有空间反射不变性 V ( − x ) = V ( x ) V(-x)=V(x) V ( − x ) = V ( x )
对于偶宇称态 :
波函数应表示为
ψ ( x ) = { A e β x , x < 0 A e − β x , x > 0 \psi(x) = \begin{cases} A\mathrm{e}^{\beta x}, & x<0 \ A\mathrm{e}^{-\beta x}, & x>0 \end{cases} ψ ( x ) = { A e β x , A e − β x , x < 0 x > 0
按照 ψ ′ \psi' ψ ′
ψ ′ ( 0 + ) − ψ ′ ( 0 − ) = − 2 m γ ℏ 2 ψ ( 0 ) ⇓ − A β − A β = − 2 m γ ℏ 2 A \psi'(0^+) - \psi'(0^-) = -\frac{2m\gamma}{\hbar^2} \psi(0) \ \Downarrow \ -A\beta - A\beta = -\frac{2m\gamma}{\hbar^2}A ψ ′ ( 0 + ) − ψ ′ ( 0 − ) = − ℏ 2 2 mγ ψ ( 0 ) ⇓ − A β − A β = − ℏ 2 2 mγ A
可得
β = m γ ℏ 2 \beta = \frac{m\gamma}{\hbar^2} β = ℏ 2 mγ
则可得出粒子的能量本征值
β = m γ ℏ 2 = − 2 m E ℏ ⟹ E = − m γ 2 2 ℏ 2 \beta = \frac{m\gamma}{\hbar^2} = \frac{\sqrt{-2mE}}{\hbar} \Longrightarrow E = -\frac{m\gamma^2}{2\hbar^2} β = ℏ 2 mγ = ℏ − 2 m E ⟹ E = − 2 ℏ 2 m γ 2
由归一化条件可得
( ψ , ψ ) = 2 ∫ 0 + ∞ ∣ A ∣ 2 e − 2 β x d x = ∣ A ∣ 2 β = 1 (\psi,\psi) = 2\int_{0}^{+\infty} |A|^2\mathrm{e}^{-2\beta x} \mathrm{d}x = \frac{|A|^2}{\beta} = 1 ( ψ , ψ ) = 2 ∫ 0 + ∞ ∣ A ∣ 2 e − 2 β x d x = β ∣ A ∣ 2 = 1
取 δ \delta δ
L = 1 β = ℏ 2 m γ L = \frac{1}{\beta} =\frac{\hbar^2}{m\gamma} L = β 1 = mγ ℏ 2
则
∣ A ∣ = β = 1 L |A| = \sqrt{\beta} = \frac{1}{\sqrt{L}} ∣ A ∣ = β = L 1
这样归一化的束缚能量本征态波函数可表示为
ψ ( x ) = 1 L e − ∣ x ∣ L \psi(x) = \frac{1}{\sqrt{L}} \mathrm{e}^{-\frac{|x|}{L}} ψ ( x ) = L 1 e − L ∣ x ∣
对于奇宇称态 :
波函数应表示为
ψ ( x ) = { A e β x , x < 0 − A e − β x , x > 0 \psi(x) = \begin{cases} A\mathrm{e}^{\beta x}, & x<0 \ -A\mathrm{e}^{-\beta x}, & x>0 \end{cases} ψ ( x ) = { A e β x , − A e − β x , x < 0 x > 0
由波函数在 x = 0 x=0 x = 0
ψ ( 0 − ) = ψ ( 0 + ) ⟹ A = − A ⟹ A = 0 \psi(0^-) = \psi(0^+) \Longrightarrow A = -A \Longrightarrow A = 0 ψ ( 0 − ) = ψ ( 0 + ) ⟹ A = − A ⟹ A = 0
所以不可能存在奇宇称束缚能量本征态。
从物理上考虑,奇宇称波函数在 x = 0 x=0 x = 0 δ \delta δ x = 0 x=0 x = 0 δ \delta δ
设具有一定能量 E E E m m m x x x
V ( x ) = { V 0 , 0 < x < a 0 , x < 0 , x > a V(x) = \begin{cases} V_0\ , & 0<x<a \ 0\ , & x<0,x>a \end{cases} V ( x ) = { V 0 , 0 , 0 < x < a x < 0 , x > a
无论粒子能量 E > V 0 E>V_0 E > V 0 E < V 0 E<V_0 E < V 0 0 < E < V 0 0<E<V_0 0 < E < V 0
k = 2 m E ℏ , κ = 2 m ( V 0 − E ) ℏ k = \frac{\sqrt{2mE}}{\hbar}, \kern 1em \kappa = \frac{\sqrt{2m(V_0-E)}}{\hbar} k = ℏ 2 m E , κ = ℏ 2 m ( V 0 − E )
则波函数为
ψ ( x ) = { e i k x + R e − i k x , x < 0 A e κ x + B e − κ x , 0 < x < a S e i k x , x > a \psi(x) = \begin{cases} \mathrm{e}^{\mathrm{i}kx}+R\mathrm{e}^{-\mathrm{i}kx}\ , & x<0 \ A\mathrm{e}^{\kappa x}+B\mathrm{e}^{-\kappa x}\ , & 0<x<a \ S\mathrm{e}^{\mathrm{i}kx}\ , & x>a \end{cases} ψ ( x ) = ⎩ ⎨ ⎧ e i k x + R e − i k x , A e κ x + B e − κ x , S e i k x , x < 0 0 < x < a x > a
其中 R e − i k x R\mathrm{e}^{-\mathrm{i}kx} R e − i k x S e i k x S\mathrm{e}^{\mathrm{i}kx} S e i k x
透射系数 为
T = ∣ S ∣ 2 = 4 k 2 κ 2 ( k 2 + κ 2 ) 2 sinh 2 ( κ a ) + 4 k 2 κ 2 = [ 1 + 1 4 E V 0 ( 1 − E V 0 ) sinh 2 ( κ a ) ] − 1 T = |S|^2 = \frac{4k^2\kappa^2}{(k^2+\kappa^2)^2\sinh^2(\kappa a)+4k^2\kappa^2} = \left[1+\frac{1}{\frac{4E}{V_0}(1-\frac{E}{V_0})}\sinh^2(\kappa a)\right]^{-1} T = ∣ S ∣ 2 = ( k 2 + κ 2 ) 2 sinh 2 ( κa ) + 4 k 2 κ 2 4 k 2 κ 2 = [ 1 + V 0 4 E ( 1 − V 0 E ) 1 sinh 2 ( κa ) ] − 1
反射系数 为
∣ R ∣ 2 = ( k 2 + κ 2 ) 2 sinh 2 ( κ a ) ( k 2 + κ 2 ) 2 sinh 2 ( κ a ) + 4 k 2 κ 2 |R|^2 = \frac{(k^2+\kappa^2)^2\sinh^2(\kappa a)}{(k^2+\kappa^2)^2\sinh^2(\kappa a)+4k^2\kappa^2} ∣ R ∣ 2 = ( k 2 + κ 2 ) 2 sinh 2 ( κa ) + 4 k 2 κ 2 ( k 2 + κ 2 ) 2 sinh 2 ( κa )
在势垒外 ( x < 0 , x > a ) (x<0,x>a) ( x < 0 , x > a )
ψ ′ ′ ( x ) + 2 m E ℏ 2 ψ ( x ) = 0 \psi''(x) + \frac{2mE}{\hbar^2}\psi(x) = 0 ψ ′′ ( x ) + ℏ 2 2 m E ψ ( x ) = 0
令 k = 2 m E ℏ k=\frac{\sqrt{2mE}}{\hbar} k = ℏ 2 m E ψ ( x ) ∼ e ± i k x \psi(x) \sim \mathrm{e}^{\pm\mathrm{i}kx} ψ ( x ) ∼ e ± i k x x < a x<a x < a 入射波 e i k x \mathrm{e}^{\mathrm{i}kx} e i k x 反射波 e − i k x \mathrm{e}^{-\mathrm{i}kx} e − i k x x > a x>a x > a 透射波 e i k x \mathrm{e}^{\mathrm{i}kx} e i k x
ψ ( x ) = { e i k x + R e − i k x , x < 0 S e i k x , x > a \psi(x) = \begin{cases} \mathrm{e}^{\mathrm{i}kx}+R\mathrm{e}^{-\mathrm{i}kx}\ , & x<0 \ S\mathrm{e}^{\mathrm{i}kx}\ , & x>a \end{cases} ψ ( x ) = { e i k x + R e − i k x , S e i k x , x < 0 x > a
这里把入射波的波幅任意地取为 1 1 1
在势垒内部 ( 0 < x < a ) (0<x<a) ( 0 < x < a )
ψ ′ ′ ( x ) − 2 m ( V 0 − E ) ℏ 2 ψ ( x ) = 0 \psi''(x) - \frac{2m(V_0-E)}{\hbar^2}\psi(x) = 0 ψ ′′ ( x ) − ℏ 2 2 m ( V 0 − E ) ψ ( x ) = 0
令 κ = 2 m ( V 0 − E ) ℏ \kappa=\frac{\sqrt{2m(V_0-E)}}{\hbar} κ = ℏ 2 m ( V 0 − E )
ψ ( x ) = A e κ x + B e − κ x ( 0 < x < a ) \psi(x) = A\mathrm{e}^{\kappa x}+B\mathrm{e}^{-\kappa x} \kern 2em (0<x<a) ψ ( x ) = A e κ x + B e − κ x ( 0 < x < a )
根据 ψ \psi ψ ψ ′ \psi' ψ ′ x = 0 x=0 x = 0 x = a x=a x = a R , S , A , B R,S,A,B R , S , A , B
{ 1 + R = A + B i k ( 1 − R ) = κ ( A − B ) S e i k a = A e κ a + B e − κ a i k S e i k x = κ ( A e κ a − B e − κ a ) \left{\begin{matrix} 1+R = A+B \ \mathrm{i}k(1-R) = \kappa(A-B) \ S\mathrm{e}^{\mathrm{i}ka} = A\mathrm{e}^{\kappa a}+B\mathrm{e}^{-\kappa a} \ \mathrm{i}kS\mathrm{e}^{\mathrm{i}kx} = \kappa(A\mathrm{e}^{\kappa a}-B\mathrm{e}^{-\kappa a}) \end{matrix}\right. ⎩ ⎨ ⎧ 1 + R = A + B i k ( 1 − R ) = κ ( A − B ) S e i ka = A e κa + B e − κa i k S e i k x = κ ( A e κa − B e − κa )
为了求解该方程组,可由前两个方程用 R R R A , B A,B A , B S S S A , B A,B A , B S , R S,R S , R S S S R R R A , B A,B A , B
入射的粒子流密度为
j i = − i ℏ 2 m ( ψ i ∗ d d x ψ i − ψ i d d x ψ i ∗ ) = − i ℏ 2 m ( e − i k x d d x e i k x − e i k x d d x e − i k x ) = ℏ k m = v j_i = -\frac{\mathrm{i}\hbar}{2m} (\psi_i^* \frac{\mathrm{d}}{\mathrm{d}x} \psi_i - \psi_i \frac{\mathrm{d}}{\mathrm{d}x} \psi_i^*) = -\frac{\mathrm{i}\hbar}{2m} (\mathrm{e}^{-\mathrm{i}kx} \frac{\mathrm{d}}{\mathrm{d}x} \mathrm{e}^{\mathrm{i}kx} - \mathrm{e}^{\mathrm{i}kx} \frac{\mathrm{d}}{\mathrm{d}x} \mathrm{e}^{-\mathrm{i}kx}) = \frac{\hbar k}{m} = v j i = − 2 m i ℏ ( ψ i ∗ d x d ψ i − ψ i d x d ψ i ∗ ) = − 2 m i ℏ ( e − i k x d x d e i k x − e i k x d x d e − i k x ) = m ℏ k = v
类似的,可以计算出反射流密度 j r j_r j r j t j_t j t
j r = − ∣ R ∣ 2 v , j t = ∣ S ∣ 2 v j_r = -|R|^2v , \kern 1em j_t = |S|^2v j r = − ∣ R ∣ 2 v , j t = ∣ S ∣ 2 v
所以
反射系数 = ∣ j r ∣ ∣ j i ∣ = ∣ R ∣ 2 透射系数 = ∣ j t ∣ ∣ j i ∣ = ∣ S ∣ 2 反射系数 = \frac{|j_r|}{|j_i|} = |R|^2 \ \kern 1em \ 透射系数 = \frac{|j_t|}{|j_i|} = |S|^2 反射系数 = ∣ j i ∣ ∣ j r ∣ = ∣ R ∣ 2 透射系数 = ∣ j i ∣ ∣ j t ∣ = ∣ S ∣ 2
代入求解方程组得到的 R , S R,S R , S
透射系数 为
T = ∣ S ∣ 2 = 4 k 2 κ 2 ( k 2 + κ 2 ) 2 sinh 2 ( κ a ) + 4 k 2 κ 2 T = |S|^2 = \frac{4k^2\kappa^2}{(k^2+\kappa^2)^2\sinh^2(\kappa a)+4k^2\kappa^2} T = ∣ S ∣ 2 = ( k 2 + κ 2 ) 2 sinh 2 ( κa ) + 4 k 2 κ 2 4 k 2 κ 2
反射系数 为
∣ R ∣ 2 = ( k 2 + κ 2 ) 2 sinh 2 ( κ a ) ( k 2 + κ 2 ) 2 sinh 2 ( κ a ) + 4 k 2 κ 2 |R|^2 = \frac{(k^2+\kappa^2)^2\sinh^2(\kappa a)}{(k^2+\kappa^2)^2\sinh^2(\kappa a)+4k^2\kappa^2} ∣ R ∣ 2 = ( k 2 + κ 2 ) 2 sinh 2 ( κa ) + 4 k 2 κ 2 ( k 2 + κ 2 ) 2 sinh 2 ( κa )
∣ R ∣ 2 + ∣ S ∣ 2 = 1 |R|^2 + |S|^2 = 1 ∣ R ∣ 2 + ∣ S ∣ 2 = 1
通过整理,透射系数还可以表示为
T = [ 1 + 1 4 E V 0 ( 1 − E V 0 ) sinh 2 ( κ a ) ] − 1 T = \left[1+\frac{1}{\frac{4E}{V_0}(1-\frac{E}{V_0})}\sinh^2(\kappa a)\right]^{-1} T = [ 1 + V 0 4 E ( 1 − V 0 E ) 1 sinh 2 ( κa ) ] − 1
当 0 < E < V 0 0<E<V_0 0 < E < V 0 T ≠ 0 T\ne0 T = 0 量子隧穿效应 (或称隧道效应 (tunnel effect)、势垒贯穿 ),它是粒子具有波动性的表现。当然,这种现象一般概率较低,只有在一定的条件下才比较显著。
设 κ a ≫ 1 \kappa a\gg1 κa ≫ 1 sinh ( κ a ) = 1 2 ( e κ a − e − κ a ) ≈ 1 2 e κ a ≫ 1 \sinh(\kappa a) = \frac12(\mathrm{e}^{\kappa a}-\mathrm{e}^{-\kappa a}) \approx \frac12\mathrm{e}^{\kappa a} \gg 1 sinh ( κa ) = 2 1 ( e κa − e − κa ) ≈ 2 1 e κa ≫ 1
T ≈ 4 k 2 κ 2 ( k 2 + κ 2 ) 2 sinh 2 ( κ a ) ≈ 4 k 2 κ 2 ( k 2 + κ 2 ) 2 ( 1 2 e κ a ) 2 = 16 k 2 κ 2 ( k 2 + κ 2 ) 2 e − 2 κ a = 16 E ( V 0 − E ) V 0 2 e − 2 a ℏ 2 m ( V 0 − E ) T \approx \frac{4k^2\kappa^2}{(k^2+\kappa^2)^2\sinh^2(\kappa a)} \approx \frac{4k^2\kappa^2}{(k^2+\kappa^2)^2(\frac12\mathrm{e}^{\kappa a})^2} = \frac{16k^2\kappa^2}{(k^2+\kappa^2)^2}\mathrm{e}^{-2\kappa a} = \frac{16E(V_0-E)}{V_0^2}\mathrm{e}^{-\frac{2a}{\hbar}\sqrt{2m(V_0-E)}} T ≈ ( k 2 + κ 2 ) 2 sinh 2 ( κa ) 4 k 2 κ 2 ≈ ( k 2 + κ 2 ) 2 ( 2 1 e κa ) 2 4 k 2 κ 2 = ( k 2 + κ 2 ) 2 16 k 2 κ 2 e − 2 κa = V 0 2 16 E ( V 0 − E ) e − ℏ 2 a 2 m ( V 0 − E )
若记
T 0 = 16 E V 0 ( 1 − E V 0 ) T_0 = 16 \frac{E}{V_0} \left(1-\frac{E}{V_0}\right) T 0 = 16 V 0 E ( 1 − V 0 E )
则
T ≈ T 0 exp ( − 2 a ℏ 2 m ( V 0 − E ) ) T \approx T_0 \exp\left(-\frac{2a}{\hbar}\sqrt{2m(V_0-E)}\right) T ≈ T 0 exp ( − ℏ 2 a 2 m ( V 0 − E ) )
可以看出 T T T m m m a a a ( V 0 − E ) (V_0-E) ( V 0 − E )
对于一般形状的势垒,可以将其视为许多方势垒相邻排布,若透射系数 T ≪ 1 T\ll1 T ≪ 1 a ≤ x ≤ b a\le x\le b a ≤ x ≤ b
T ≈ T 0 exp { − 2 ℏ ∫ a b 2 m [ V ( x ) − E ] d x } T \approx T_0 \exp\left{ -\frac{2}{\hbar} \int_a^b \sqrt{2m[V(x)-E]}\ \mathrm{d}x \right} T ≈ T 0 exp { − ℏ 2 ∫ a b 2 m [ V ( x ) − E ] d x }
首先考虑方势垒中 E > V 0 E>V_0 E > V 0
k ′ = 2 m ( E − V 0 ) ℏ k' = \frac{\sqrt{2m(E-V_0)}}{\hbar} k ′ = ℏ 2 m ( E − V 0 )
只需要将 κ ⟶ i k ′ \kappa \longrightarrow \mathrm{i}k' κ ⟶ i k ′
T = 4 k 2 k ′ 2 ( k 2 − k ′ 2 ) 2 sin 2 ( k ′ a ) + 4 k 2 k ′ 2 = [ 1 + 1 4 ( k k ′ − k ′ k ) 2 sin 2 ( k ′ a ) ] − 1 T = \frac{4k^2k'^2}{(k^2-k'^2)^2\sin^2(k'a)+4k^2k'^2} = \left[1+\frac14 \left(\frac{k}{k'}-\frac{k'}{k}\right)^2 \sin^2(k'a)\right]^{-1} T = ( k 2 − k ′2 ) 2 sin 2 ( k ′ a ) + 4 k 2 k ′2 4 k 2 k ′2 = [ 1 + 4 1 ( k ′ k − k k ′ ) 2 sin 2 ( k ′ a ) ] − 1
当 k ′ a = n π k'a=n\pi k ′ a = nπ sin ( k ′ a ) = 0 \sin(k'a)=0 sin ( k ′ a ) = 0 T = 1 T=1 T = 1 共振透射 。
而对于方势阱的透射,上述理论仍然适用,只需要把 V 0 ⟶ − V 0 V_0 \longrightarrow -V_0 V 0 ⟶ − V 0
k ′ = 2 m ( E + V 0 ) ℏ ≥ 2 m E ℏ = k k' = \frac{\sqrt{2m(E+V_0)}}{\hbar} \ge \frac{\sqrt{2mE}}{\hbar} = k k ′ = ℏ 2 m ( E + V 0 ) ≥ ℏ 2 m E = k
此时透射系数
T = [ 1 + 1 4 ( k k ′ − k ′ k ) 2 sin 2 ( k ′ a ) ] − 1 = [ 1 + sin 2 ( k ′ a ) 4 E V 0 ( 1 + E V 0 ) ] − 1 T = \left[1+\frac14 \left(\frac{k}{k'}-\frac{k'}{k}\right)^2 \sin^2(k'a)\right]^{-1} = \left[1 + \frac{\sin^2(k'a)}{4\frac{E}{V_0}\left(1+\frac{E}{V_0}\right)}\right]^{-1} T = [ 1 + 4 1 ( k ′ k − k k ′ ) 2 sin 2 ( k ′ a ) ] − 1 = 1 + 4 V 0 E ( 1 + V 0 E ) sin 2 ( k ′ a ) − 1
可以看出,若 V 0 = 0 V_0=0 V 0 = 0 T = 1 T=1 T = 1 V 0 ≠ 0 V_0\ne0 V 0 = 0 T < 1 , ∣ R ∣ 2 ≠ 0 T<1,|R|^2\ne0 T < 1 , ∣ R ∣ 2 = 0
对于给定势阱,透射系数 T T T E E E T ( E ) T(E) T ( E ) E E E
如果 E ≪ V 0 E \ll V_0 E ≪ V 0 T T T E E E sin ( k ′ a ) = 0 \sin(k'a)=0 sin ( k ′ a ) = 0 T = 1 T=1 T = 1 ∣ R ∣ 2 = 0 |R|^2=0 ∣ R ∣ 2 = 0 共振透射 ,它出现的条件是
k ′ a = n π ( n = 1 , 2 , 3 , ⋯ ) k'a = n\pi \kern 2em (n=1,2,3,\cdots) k ′ a = nπ ( n = 1 , 2 , 3 , ⋯ )
可以得到共振能级 E n E_n E n
k ′ = 2 m ( E + V 0 ) ℏ = n π a ⟹ E n = − V 0 + n 2 π 2 ℏ 2 2 m a 2 k' = \frac{\sqrt{2m(E+V_0)}}{\hbar} = \frac{n\pi}{a} \Longrightarrow E_n = -V_0 + \frac{n^2\pi^2\hbar^2}{2ma^2} k ′ = ℏ 2 m ( E + V 0 ) = a nπ ⟹ E n = − V 0 + 2 m a 2 n 2 π 2 ℏ 2
与此相对,反射最强的条件是
k ′ a = ( n + 1 2 ) π ( n = 0 , 1 , 2 , ⋯ ) k'a = (n+\frac12)\pi \kern 2em (n=0,1,2,\cdots) k ′ a = ( n + 2 1 ) π ( n = 0 , 1 , 2 , ⋯ )
设具有一定能量 E E E m m m x x x δ \delta δ
V ( x ) = γ δ ( x ) ( γ > 0 ) V(x) = \gamma\delta(x) \kern 2em (\gamma>0) V ( x ) = γ δ ( x ) ( γ > 0 )
能量本征方程为
ψ ′ ′ ( x ) = − 2 m ℏ 2 [ E − γ δ ( x ) ] ψ ( x ) \psi''(x) = -\frac{2m}{\hbar^2} \left[E-\gamma\delta(x)\right] \psi(x) ψ ′′ ( x ) = − ℏ 2 2 m [ E − γ δ ( x ) ] ψ ( x )
左右两边同时积分可以得到 δ \delta δ ψ ′ \psi' ψ ′ 跃变条件 :
lim ε → 0 + ∫ − ε ε ψ ′ ′ ( x ) d x = lim ε → 0 + ∫ − ε ε − 2 m ℏ 2 [ E − γ δ ( x ) ] ψ ( x ) d x ⇓ ψ ′ ( 0 + ) − ψ ′ ( 0 − ) = 2 m γ ℏ 2 ψ ( 0 ) \lim_{\varepsilon\to0^+} \int_{-\varepsilon}^{\varepsilon} \psi''(x) \mathrm{d}x = \lim_{\varepsilon\to0^+} \int_{-\varepsilon}^{\varepsilon} -\frac{2m}{\hbar^2} \left[E-\gamma\delta(x)\right] \psi(x) \mathrm{d}x \ \Downarrow \ \psi'(0^+) - \psi'(0^-) = \frac{2m\gamma}{\hbar^2} \psi(0) ε → 0 + lim ∫ − ε ε ψ ′′ ( x ) d x = ε → 0 + lim ∫ − ε ε − ℏ 2 2 m [ E − γ δ ( x ) ] ψ ( x ) d x ⇓ ψ ′ ( 0 + ) − ψ ′ ( 0 − ) = ℏ 2 2 mγ ψ ( 0 )
令
k = 2 m E ℏ > 0 k = \frac{\sqrt{2mE}}{\hbar} > 0 k = ℏ 2 m E > 0
则在 x ≠ 0 x\ne0 x = 0
ψ ′ ′ ( x ) + k 2 ψ ( x ) = 0 \psi''(x) + k^2\psi(x) = 0 ψ ′′ ( x ) + k 2 ψ ( x ) = 0
该方程的两个线性无关解可取为 ψ ( x ) ∼ e ± i k x \psi(x) \sim \mathrm{e}^{\pm\mathrm{i}kx} ψ ( x ) ∼ e ± i k x x < 0 x<0 x < 0 入射波 e i k x \mathrm{e}^{\mathrm{i}kx} e i k x 反射波 e − i k x \mathrm{e}^{-\mathrm{i}kx} e − i k x x > 0 x>0 x > 0 透射波 e i k x \mathrm{e}^{\mathrm{i}kx} e i k x
ψ ( x ) = { e i k x + R e − i k x , x < 0 S e i k x , x > 0 \psi(x) = \begin{cases} \mathrm{e}^{\mathrm{i}kx}+R\mathrm{e}^{-\mathrm{i}kx}\ , & x<0 \ S\mathrm{e}^{\mathrm{i}kx}\ , & x>0 \end{cases} ψ ( x ) = { e i k x + R e − i k x , S e i k x , x < 0 x > 0
根据在 x = 0 x=0 x = 0 ψ \psi ψ ψ ′ \psi' ψ ′ R , S R,S R , S
{ 1 + R = S i k S − i k ( 1 − R ) = 2 m γ ℏ 2 S \left{\begin{matrix} 1+R = S \ \mathrm{i}kS - \mathrm{i}k(1-R) = \frac{2m\gamma}{\hbar^2}S \end{matrix}\right. { 1 + R = S i k S − i k ( 1 − R ) = ℏ 2 2 mγ S
解得
S = 1 1 + i m γ ℏ 2 k R = − i m γ ℏ 2 k 1 + i m γ ℏ 2 k S = \frac{1}{1+\frac{\mathrm{i}m\gamma}{\hbar^2k}} \ \kern 1em \ R = \frac{-\frac{\mathrm{i}m\gamma}{\hbar^2k}}{1+\frac{\mathrm{i}m\gamma}{\hbar^2k}} S = 1 + ℏ 2 k i mγ 1 R = 1 + ℏ 2 k i mγ − ℏ 2 k i mγ
则透射系数 为
T = ∣ S ∣ 2 = 1 1 + m 2 γ 2 ℏ 4 k 2 = 1 1 + m γ 2 2 ℏ 2 E T = |S|^2 = \frac{1}{1+\frac{m^2\gamma^2}{\hbar^4k^2}} = \frac{1}{1+\frac{m\gamma^2}{2\hbar^2E}} T = ∣ S ∣ 2 = 1 + ℏ 4 k 2 m 2 γ 2 1 = 1 + 2 ℏ 2 E m γ 2 1
反射系数 为
∣ R ∣ 2 = m 2 γ 2 ℏ 4 k 2 1 + m 2 γ 2 ℏ 4 k 2 = m γ 2 2 ℏ 2 E 1 + m γ 2 2 ℏ 2 E |R|^2 = \frac{\frac{m^2\gamma^2}{\hbar^4k^2}}{1+\frac{m^2\gamma^2}{\hbar^4k^2}} = \frac{\frac{m\gamma^2}{2\hbar^2E}}{1+\frac{m\gamma^2}{2\hbar^2E}} ∣ R ∣ 2 = 1 + ℏ 4 k 2 m 2 γ 2 ℏ 4 k 2 m 2 γ 2 = 1 + 2 ℏ 2 E m γ 2 2 ℏ 2 E m γ 2
∣ R ∣ 2 + ∣ S ∣ 2 = 1 |R|^2 + |S|^2 = 1 ∣ R ∣ 2 + ∣ S ∣ 2 = 1
如果把 δ \delta δ δ \delta δ γ ⟶ − γ \gamma\longrightarrow-\gamma γ ⟶ − γ
δ \delta δ L = ℏ 2 m γ L=\frac{\hbar^2}{m\gamma} L = mγ ℏ 2 m γ 2 ℏ 2 \frac{m\gamma^2}{\hbar^2} ℏ 2 m γ 2
透射波的波幅 S S S m γ ℏ 2 k = 1 k / ℏ 2 m γ \frac{m\gamma}{\hbar^2k} = \frac{1}{k} / \frac{\hbar^2}{m\gamma} ℏ 2 k mγ = k 1 / mγ ℏ 2 δ \delta δ T T T m γ 2 ℏ 2 E = m γ 2 ℏ 2 / E \frac{m\gamma^2}{\hbar^2E} = \frac{m\gamma^2}{\hbar^2} / E ℏ 2 E m γ 2 = ℏ 2 m γ 2 / E E ≫ m γ 2 ℏ 2 E \gg \frac{m\gamma^2}{\hbar^2} E ≫ ℏ 2 m γ 2 T ≈ 1 T\approx1 T ≈ 1 δ \delta δ
算符是作用于波函数把它变成另一个函数的运算符号,代表力学量 A A A A ^ \hat{A} A ^ A A A A ^ \hat{A} A ^
为强调算符的特点,常常在算符的符号上加一个 “^ \hat{\kern 1em} ^ ^ \hat{\kern 1em} ^
在全部量子理论中,时间一直保持为连续变化的参量,不存在相应的“时间算符” 。
此小节之后搬运了第一章的内容,主要是从平均值的角度引出算符。
粒子处于波函数 ψ ( r ⃗ ) \psi(\vec{r}) ψ ( r ) 确定的概率分布 ,因而有确定的平均值 (又叫期待值 )。在任意状态 ψ \psi ψ A A A
A ˉ = ( ψ , A ^ ψ ) ( ψ , ψ ) \bar{A} = \frac{(\psi,\hat{A}\psi)}{(\psi,\psi)} A ˉ = ( ψ , ψ ) ( ψ , A ^ ψ )
其中 A ^ \hat{A} A ^ A A A
A ˉ = ( ψ , A ^ ψ ) \bar{A} = (\psi,\hat{A}\psi) A ˉ = ( ψ , A ^ ψ )
在波函数 ψ \psi ψ x x x
x ˉ = ∫ − ∞ + ∞ ∣ ψ ( r ⃗ ) ∣ 2 x d 3 r = ∫ − ∞ + ∞ ψ ∗ ( r ⃗ ) x ψ ( r ⃗ ) d 3 r \bar{x} = \int_{-\infty}^{+\infty} \left|\psi(\vec{r})\right|^2, x, \mathrm{d}^3r= \int_{-\infty}^{+\infty} \psi^*(\vec{r}), x, \psi(\vec{r}), \mathrm{d}^3r x ˉ = ∫ − ∞ + ∞ ∣ ψ ( r ) ∣ 2 x d 3 r = ∫ − ∞ + ∞ ψ ∗ ( r ) x ψ ( r ) d 3 r
可以得到坐标表象下的坐标算符为
x ^ = x \hat{x} = x x ^ = x
同理
y ^ = y , z ^ = z , r ⃗ ^ = r ⃗ \hat{y} = y,\kern 12pt\hat{z} = z,\kern 12pt\hat{\vec{r}} = \vec{r} y ^ = y , z ^ = z , r ^ = r
如果状态用动量表象波函数 φ ( p ⃗ ) \varphi(\vec{p}) φ ( p )
p ⃗ ˉ = ∫ − ∞ + ∞ ∣ φ ( p ⃗ ) ∣ 2 p ⃗ d 3 p = ∫ − ∞ + ∞ φ ∗ ( p ⃗ ) p ⃗ φ ( p ⃗ ) d 3 p \bar{\vec{p}} = \int_{-\infty}^{+\infty} \left|\varphi(\vec{p})\right|^2, \vec{p}, \mathrm{d}^3p= \int_{-\infty}^{+\infty} \varphi^*(\vec{p}), \vec{p}, \varphi(\vec{p}), \mathrm{d}^3p p ˉ = ∫ − ∞ + ∞ ∣ φ ( p ) ∣ 2 p d 3 p = ∫ − ∞ + ∞ φ ∗ ( p ) p φ ( p ) d 3 p
可以得到动量表象下的动量算符为
p ⃗ ^ = p ⃗ , p ^ x = p x , p ^ y = p y , p ^ z = p z \hat{\vec{p}} = \vec{p},\kern 12pt\hat{p}_x = p_x,\kern 12pt\hat{p}_y = p_y,\kern 12pt\hat{p}_z = p_z p ^ = p , p ^ x = p x , p ^ y = p y , p ^ z = p z
通过表象的转换,可以推得坐标表象下的动量算符为
p ⃗ ^ = − i ℏ ∇ , p ^ x = − i ℏ ∂ ∂ x , p ^ y = − i ℏ ∂ ∂ y , p ^ z = − i ℏ ∂ ∂ z \hat{\vec{p}} = -\mathrm{i}\hbar\nabla,\kern 12pt\hat{p}_x = -\mathrm{i}\hbar \frac{\partial}{\partial x},\kern 12pt\hat{p}_y = -\mathrm{i}\hbar \frac{\partial}{\partial y},\kern 12pt\hat{p}_z = -\mathrm{i}\hbar \frac{\partial}{\partial z} p ^ = − i ℏ∇ , p ^ x = − i ℏ ∂ x ∂ , p ^ y = − i ℏ ∂ y ∂ , p ^ z = − i ℏ ∂ z ∂
动量表象下的坐标算符为
r ⃗ ^ = i ℏ ∂ ∂ p ⃗ , x ^ = i ℏ ∂ ∂ p x , y ^ = i ℏ ∂ ∂ p y , z ^ = i ℏ ∂ ∂ p z \hat{\vec{r}} = \mathrm{i}\hbar \frac{\partial}{\partial \vec{p}},\kern 12pt\hat{x} = \mathrm{i}\hbar \frac{\partial}{\partial p_x},\kern 12pt\hat{y} = \mathrm{i}\hbar \frac{\partial}{\partial p_y},\kern 12pt\hat{z} = \mathrm{i}\hbar \frac{\partial}{\partial p_z} r ^ = i ℏ ∂ p ∂ , x ^ = i ℏ ∂ p x ∂ , y ^ = i ℏ ∂ p y ∂ , z ^ = i ℏ ∂ p z ∂
注:梯度、散度、旋度的介绍以及其在各种坐标系下的表示,可参考魏斌老师的课件 。这里给出柱坐标与球坐标下的梯度算符,
柱坐标 ( r , ϕ , z ) (r,\phi,z) ( r , ϕ , z )
∇ f = ∂ f ∂ r e ⃗ r + 1 r ∂ f ∂ θ e ⃗ θ + ∂ f ∂ z e ⃗ z \nabla f = \frac{\partial f}{\partial r}\vec{e}r + \frac{1}{r}\frac{\partial f}{\partial \theta}\vec{e} \theta + \frac{\partial f}{\partial z}\vec{e}_z ∇ f = ∂ r ∂ f e r + r 1 ∂ θ ∂ f e θ + ∂ z ∂ f e z
球坐标 ( r , θ , φ ) (r,\theta,\varphi) ( r , θ , φ )
∇ f = ∂ f ∂ r e ⃗ r + 1 r ∂ f ∂ θ e ⃗ θ + 1 r sin θ ∂ f ∂ φ e ⃗ φ \nabla f = \frac{\partial f}{\partial r}\vec{e}r + \frac{1}{r}\frac{\partial f}{\partial \theta}\vec{e} \theta + \frac{1}{r\sin\theta}\frac{\partial f}{\partial \varphi}\vec{e}_\varphi ∇ f = ∂ r ∂ f e r + r 1 ∂ θ ∂ f e θ + r sin θ 1 ∂ φ ∂ f e φ
对于有经典对应的力学量,例如动能、势能和轨道角动量,由经典力学中的函数形式假定量子力学中的算符形式,可以由坐标算符与动量算符通过运算得到,即
A = A ( r ⃗ , p ⃗ ) ⟹ A ^ = A ( r ⃗ ^ , p ⃗ ^ ) A = A(\vec{r},\vec{p})\Longrightarrow\hat{A} = A(\hat{\vec{r}},\hat{\vec{p}}) A = A ( r , p ) ⟹ A ^ = A ( r ^ , p ^ )
如一维谐振子的能量算符
H = ( p x ) 2 2 m + 1 2 k x 2 ⟹ H ^ = ( p ^ x ) 2 2 m + 1 2 k x ^ 2 H = \frac{(p_x)^2}{2m} + \frac12kx^2\Longrightarrow\hat{H} = \frac{(\hat{p}_x)^2}{2m} + \frac12k\hat{x}^2 H = 2 m ( p x ) 2 + 2 1 k x 2 ⟹ H ^ = 2 m ( p ^ x ) 2 + 2 1 k x ^ 2
如粒子的轨道角动量算符
L ⃗ = r ⃗ × p ⃗ ⟹ L ⃗ ^ = r ⃗ ^ × p ⃗ ^ = ∣ i ⃗ j ⃗ k ⃗ x ^ y ^ z ^ p ^ x p ^ y p ^ z ∣ \vec{L} = \vec{r} \times \vec{p}\Longrightarrow\hat{\vec{L}} = \hat{\vec{r}} \times \hat{\vec{p}}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \ \hat{x} & \hat{y} & \hat{z} \ \hat{p}_x & \hat{p}_y & \hat{p}_z\end{vmatrix} L = r × p ⟹ L ^ = r ^ × p ^ = i x ^ p ^ x j y ^ p ^ y k z ^ p ^ z
L ^ x = y ^ p ^ z − z ^ p ^ y L ^ y = z ^ p ^ x − x ^ p ^ z L ^ z = x ^ p ^ y − y ^ p ^ x \hat{L}_x = \hat{y}\hat{p}_z - \hat{z}\hat{p}_y\\kern 12pt\\hat{L}_y = \hat{z}\hat{p}_x - \hat{x}\hat{p}_z\\kern 12pt\\hat{L}_z = \hat{x}\hat{p}_y - \hat{y}\hat{p}_x L ^ x = y ^ p ^ z − z ^ p ^ y L ^ y = z ^ p ^ x − x ^ p ^ z L ^ z = x ^ p ^ y − y ^ p ^ x
在坐标表象下,上述算符的表达式为
H ^ = − ℏ 2 2 m d 2 d x 2 + 1 2 k x 2 \hat{H} = -\frac{\hbar^2}{2m} \frac{\mathrm{d}^2}{\mathrm{d}x^2} + \frac12kx^2 H ^ = − 2 m ℏ 2 d x 2 d 2 + 2 1 k x 2
L ⃗ ^ = r ⃗ × ( − i ℏ ∇ ) = ∣ i ⃗ j ⃗ k ⃗ x y z − i ℏ ∂ ∂ x − i ℏ ∂ ∂ y − i ℏ ∂ ∂ z ∣ \hat{\vec{L}} = \vec{r} \times (-\mathrm{i}\hbar\nabla)=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \ x & y & z \ -\mathrm{i}\hbar \frac{\partial}{\partial x} & -\mathrm{i}\hbar \frac{\partial}{\partial y} & -\mathrm{i}\hbar \frac{\partial}{\partial z}\end{vmatrix} L ^ = r × ( − i ℏ∇ ) = i x − i ℏ ∂ x ∂ j y − i ℏ ∂ y ∂ k z − i ℏ ∂ z ∂
L ^ x = − i ℏ ( y ∂ ∂ z − z ∂ ∂ y ) L ^ y = − i ℏ ( z ∂ ∂ x − x ∂ ∂ z ) L ^ z = − i ℏ ( x ∂ ∂ y − y ∂ ∂ x ) \hat{L}_x = -\mathrm{i}\hbar (y\frac{\partial}{\partial z}-z\frac{\partial}{\partial y})\\kern 12pt\\hat{L}_y = -\mathrm{i}\hbar (z\frac{\partial}{\partial x}-x\frac{\partial}{\partial z})\\kern 12pt\\hat{L}_z = -\mathrm{i}\hbar (x\frac{\partial}{\partial y}-y\frac{\partial}{\partial x}) L ^ x = − i ℏ ( y ∂ z ∂ − z ∂ y ∂ ) L ^ y = − i ℏ ( z ∂ x ∂ − x ∂ z ∂ ) L ^ z = − i ℏ ( x ∂ y ∂ − y ∂ x ∂ )
若使用球坐标系,角动量算符表示为
L ^ x = i ℏ ( sin φ ∂ ∂ θ + cot θ cos φ ∂ ∂ φ ) L ^ y = i ℏ ( − cos φ ∂ ∂ θ + cot θ sin φ ∂ ∂ φ ) L ^ z = − i ℏ ∂ ∂ φ L ^ 2 = − ℏ 2 [ 1 sin θ ∂ ∂ θ ( sin θ ∂ ∂ θ ) + 1 sin 2 θ ∂ 2 ∂ φ 2 ] \hat{L}_x = \mathrm{i}\hbar \left( \sin\varphi\frac{\partial}{\partial\theta}+\cot\theta\cos\varphi\frac{\partial}{\partial\varphi} \right) \ \kern 1em \ \hat{L}_y = \mathrm{i}\hbar \left( -\cos\varphi\frac{\partial}{\partial\theta}+\cot\theta\sin\varphi\frac{\partial}{\partial\varphi} \right) \ \kern 1em \ \hat{L}_z = -\mathrm{i}\hbar \frac{\partial}{\partial\varphi} \ \kern 1em \ \hat{L}^2 = -\hbar^2 \left[ \frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\varphi^2} \right] L ^ x = i ℏ ( sin φ ∂ θ ∂ + cot θ cos φ ∂ φ ∂ ) L ^ y = i ℏ ( − cos φ ∂ θ ∂ + cot θ sin φ ∂ φ ∂ ) L ^ z = − i ℏ ∂ φ ∂ L ^ 2 = − ℏ 2 [ sin θ 1 ∂ θ ∂ ( sin θ ∂ θ ∂ ) + sin 2 θ 1 ∂ φ 2 ∂ 2 ]
对于已归一化的波函数,力学量 A A A
A ˉ = ∫ − ∞ + ∞ ψ ∗ ( r ⃗ ) A ( r ⃗ , − i ℏ ∇ ) ψ ( r ⃗ ) d 3 r \bar{A} = \int_{-\infty}^{+\infty} \psi^*(\vec{r}), A(\vec{r},-\mathrm{i}\hbar\nabla), \psi(\vec{r}), \mathrm{d^3}r A ˉ = ∫ − ∞ + ∞ ψ ∗ ( r ) A ( r , − i ℏ∇ ) ψ ( r ) d 3 r
A ˉ = ∫ − ∞ + ∞ φ ∗ ( p ⃗ ) A ( i ℏ ∂ ∂ p ⃗ , p ⃗ ) φ ( p ⃗ ) d 3 p \bar{A} = \int_{-\infty}^{+\infty} \varphi^*(\vec{p}), A(\mathrm{i}\hbar \frac{\partial}{\partial \vec{p}},\vec{p}), \varphi(\vec{p}), \mathrm{d^3}p A ˉ = ∫ − ∞ + ∞ φ ∗ ( p ) A ( i ℏ ∂ p ∂ , p ) φ ( p ) d 3 p
对于本小节的理解,可以参照对线性代数的矩阵的理解。
对于任意复数 c 1 , c 2 c_1,c_2 c 1 , c 2 ψ 1 , ψ 2 \psi_1,\psi_2 ψ 1 , ψ 2 A ^ \hat{A} A ^ 线性算符 :
A ^ ( c 1 ψ 1 + c 2 ψ 2 ) = c 1 A ^ ψ 1 + c 2 A ^ ψ 2 \hat{A} (c_1\psi_1+c_2\psi_2) = c_1\hat{A}\psi_1 + c_2\hat{A}\psi_2 A ^ ( c 1 ψ 1 + c 2 ψ 2 ) = c 1 A ^ ψ 1 + c 2 A ^ ψ 2
刻画可观测量 的算符都是线性算符。
并非所有算符都是线性算符,如取复共轭算符,在一般情况下 ( c 1 ψ 1 + c 2 ψ 2 ) ∗ = c 1 ∗ ψ 1 ∗ + c 2 ∗ ψ 2 ∗ ≠ c 1 ψ 1 ∗ + c 2 ψ 2 ∗ (c_1\psi_1+c_2\psi_2)^* = c_1^\psi_1^ + c_2^\psi_2^ \ne c_1\psi_1^* + c_2\psi_2^* ( c 1 ψ 1 + c 2 ψ 2 ) ∗ = c 1 ∗ ψ 1 ∗ + c 2 ∗ ψ 2 ∗ = c 1 ψ 1 ∗ + c 2 ψ 2 ∗
若两个算符 A ^ , B ^ \hat{A},\hat{B} A ^ , B ^ 任意 波函数 ψ \psi ψ
A ^ ψ = B ^ ψ \hat{A} \psi = \hat{B} \psi A ^ ψ = B ^ ψ
则称这两个算符相等 ,记为 A ^ = B ^ \hat{A}=\hat{B} A ^ = B ^
算符相等的定义给出了计算或化简算符表达式的方法,即将算符表达式作用于波函数上之后再进行计算;若不作用于波函数上直接计算,有可能会计算错误。同时也应注意只有对任意波函数都成立,才可说明算符相等,只有个别波函数成立则无法说明。
单位算符 I ^ \hat{I} I ^ ψ \psi ψ
I ^ ψ = ψ \hat{I} \psi = \psi I ^ ψ = ψ
算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ A ^ + B ^ \hat{A}+\hat{B} A ^ + B ^ ψ \psi ψ
( A ^ + B ^ ) ψ = A ^ ψ + B ^ ψ (\hat{A}+\hat{B}) \psi = \hat{A} \psi + \hat{B} \psi ( A ^ + B ^ ) ψ = A ^ ψ + B ^ ψ
算符之和满足交换律 和结合律 :
A ^ + B ^ = B ^ + A ^ A ^ + ( B ^ + C ^ ) = ( A ^ + B ^ ) + C ^ \hat{A} + \hat{B} = \hat{B} + \hat{A} \ \hat{A} + (\hat{B} + \hat{C}) = (\hat{A} + \hat{B}) + \hat{C} A ^ + B ^ = B ^ + A ^ A ^ + ( B ^ + C ^ ) = ( A ^ + B ^ ) + C ^
两个线性算符之和仍为线性算符。
算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ A ^ B ^ \hat{A}\hat{B} A ^ B ^ ψ \psi ψ
( A ^ B ^ ) ψ = A ^ ( B ^ ψ ) (\hat{A}\hat{B}) \psi = \hat{A} (\hat{B}\psi) ( A ^ B ^ ) ψ = A ^ ( B ^ ψ )
即 A ^ B ^ \hat{A}\hat{B} A ^ B ^ ψ \psi ψ B ^ \hat{B} B ^ ψ \psi ψ A ^ \hat{A} A ^ ( B ^ ψ ) (\hat{B}\psi) ( B ^ ψ )
一般算符之积不满足交换律 ,即
A ^ B ^ ≠ B ^ A ^ \hat{A} \hat{B} \ne \hat{B} \hat{A} A ^ B ^ = B ^ A ^
任意算符与单位算符之间可交换,即 A ^ I ^ = I ^ A ^ \hat{A}\hat{I}=\hat{I}\hat{A} A ^ I ^ = I ^ A ^
A ^ n = A ^ A ^ ⋯ A ^ ⏟ n 个 A ^ \hat{A}^n = \underbrace{\hat{A}\hat{A}\cdots\hat{A}}_{n个\hat{A}} A ^ n = n 个 A ^ A ^ A ^ ⋯ A ^
A ^ m A ^ n = A ^ m + n \hat{A}^m \hat{A}^n = \hat{A}^{m+n} A ^ m A ^ n = A ^ m + n
已知算符 A ^ \hat{A} A ^ φ \varphi φ A ^ ψ = φ \hat{A}\psi=\varphi A ^ ψ = φ 唯一 地解出波函数 ψ \psi ψ A ^ \hat{A} A ^ 逆算符 A ^ − 1 \hat{A}^{-1} A ^ − 1
A ^ − 1 φ = ψ \hat{A}^{-1} \varphi = \psi A ^ − 1 φ = ψ
并非所有的算符都有逆算符,如投影算符就不存在逆,因为 A ^ ψ = φ \hat{A}\psi=\varphi A ^ ψ = φ
若 A ^ , B ^ \hat{A},\hat{B} A ^ , B ^ A ^ − 1 , B ^ − 1 \hat{A}^{-1},\hat{B}^{-1} A ^ − 1 , B ^ − 1
A ^ A ^ − 1 = A ^ − 1 A ^ = I ^ ( A ^ B ^ ) − 1 = B ^ − 1 A ^ − 1 \hat{A} \hat{A}^{-1} = \hat{A}^{-1} \hat{A} = \hat{I}\ (\hat{A}\hat{B})^{-1} = \hat{B}^{-1} \hat{A}^{-1} \ A ^ A ^ − 1 = A ^ − 1 A ^ = I ^ ( A ^ B ^ ) − 1 = B ^ − 1 A ^ − 1
这一部分在课上没有涉及。
对于任意的波函数 ψ , φ \psi,\varphi ψ , φ A ^ \hat{A} A ^ 转置算符 A ^ ~ \widetilde{\hat{A}} A ^
( ψ , A ^ ~ φ ) = ( φ ∗ , A ^ ψ ∗ ) (\psi,\widetilde{\hat{A}}\varphi) = (\varphi^,\hat{A}\psi^ ) ( ψ , A ^ φ ) = ( φ ∗ , A ^ ψ ∗ )
用积分表达为
∫ d τ ψ ∗ A ^ ~ φ = ∫ d τ φ A ^ ψ ∗ \int \mathrm{d}\tau\ \psi^* \widetilde{\hat{A}} \varphi = \int \mathrm{d}\tau\ \varphi \hat{A} \psi^* ∫ d τ ψ ∗ A ^ φ = ∫ d τ φ A ^ ψ ∗
即在积分式中,用 A ^ ~ \widetilde{\hat{A}} A ^ φ \varphi φ A ^ \hat{A} A ^ ψ ∗ \psi^* ψ ∗
可以证明,
A ^ B ^ = B ^ ~ \widetilde{\hat{A}\hat{B}} = \widetilde{\hat{B}} \widetilde{} A ^ B ^ = B ^
算符 A ^ \hat{A} A ^ 复共轭算符 A ^ ∗ \hat{A}^* A ^ ∗
A ^ ∗ ψ = ( A ^ ψ ∗ ) ∗ \hat{A}^* \psi = (\hat{A}\psi^)^ A ^ ∗ ψ = ( A ^ ψ ∗ ) ∗
通常算符 A ^ \hat{A} A ^ A ^ \hat{A} A ^ A ^ ∗ \hat{A}^* A ^ ∗
p ⃗ ^ ∗ = ( − i ℏ ∇ ) ∗ = i ℏ ∇ = − p ⃗ ^ \hat{\vec{p}}^* = (-\mathrm{i} \hbar \nabla)^* = \mathrm{i} \hbar \nabla = -\hat{\vec{p}} p ^ ∗ = ( − i ℏ∇ ) ∗ = i ℏ∇ = − p ^
在动量表象中
p ⃗ ^ ∗ = p ⃗ ^ \hat{\vec{p}}^* = \hat{\vec{p}} p ^ ∗ = p ^
算符 A ^ \hat{A} A ^ 厄米共轭算符 A ^ + \hat{A}^+ A ^ + A ^ † \hat{A}^{\dagger} A ^ † A ^ + \hat{A}^+ A ^ +
( ψ , A ^ + φ ) = ( A ^ ψ , φ ) (\psi , \hat{A}^+ \varphi) = (\hat{A} \psi , \varphi) ( ψ , A ^ + φ ) = ( A ^ ψ , φ )
用积分表达为
∫ d τ ψ ∗ ( A ^ + φ ) = ∫ d τ ( A ^ ψ ) ∗ φ \int \mathrm{d}\tau\ \psi^* (\hat{A}^+ \varphi) = \int \mathrm{d}\tau\ (\hat{A} \psi)^* \varphi ∫ d τ ψ ∗ ( A ^ + φ ) = ∫ d τ ( A ^ ψ ) ∗ φ
厄米共轭算符有如下性质:
( A ^ + ) + = A ^ ( A ^ + B ^ ) + = A ^ + + B ^ + ( A ^ B ^ ) + = B ^ + A ^ + (\hat{A}^+)^+ = \hat{A} \ (\hat{A} + \hat{B})^+ = \hat{A}^+ + \hat{B}^+ \ (\hat{A}\hat{B})^+ = \hat{B}^+ \hat{A}^+ ( A ^ + ) + = A ^ ( A ^ + B ^ ) + = A ^ + + B ^ + ( A ^ B ^ ) + = B ^ + A ^ +
对于任意波函数 ψ , φ \psi,\varphi ψ , φ A ^ \hat{A} A ^
( ψ , A ^ φ ) = ( A ^ ψ , φ ) (\psi , \hat{A} \varphi) = (\hat{A}\psi , \varphi) ( ψ , A ^ φ ) = ( A ^ ψ , φ )
则 A ^ \hat{A} A ^ 厄米算符 ,也称自共轭算符 。
上述条件用积分表达为
∫ d τ ψ ∗ ( A ^ φ ) = ∫ d τ ( A ^ ψ ) ∗ φ \int \mathrm{d}\tau\ \psi^* (\hat{A} \varphi) = \int \mathrm{d}\tau\ (\hat{A} \psi)^* \varphi ∫ d τ ψ ∗ ( A ^ φ ) = ∫ d τ ( A ^ ψ ) ∗ φ
与厄米共轭算符的定义相对比,可知若 A ^ + = A ^ \hat{A}^+ = \hat{A} A ^ + = A ^ A ^ \hat{A} A ^ 厄米算符 。
两个厄米算符 A ^ , B ^ \hat{A},\hat{B} A ^ , B ^ ( A ^ + B ^ ) + = A ^ + + B ^ + = A ^ + B ^ (\hat{A}+\hat{B})^+ = \hat{A}^+ + \hat{B}^+ = \hat{A} + \hat{B} ( A ^ + B ^ ) + = A ^ + + B ^ + = A ^ + B ^ A ^ , B ^ \hat{A},\hat{B} A ^ , B ^ ( A ^ B ^ ) + = B ^ + A ^ + = B ^ A ^ (\hat{A}\hat{B})^+ = \hat{B}^+ \hat{A}^+ = \hat{B}\hat{A} ( A ^ B ^ ) + = B ^ + A ^ + = B ^ A ^ A ^ , B ^ \hat{A},\hat{B} A ^ , B ^ ( A ^ B ^ ) + = A ^ B ^ (\hat{A}\hat{B})^+ = \hat{A}\hat{B} ( A ^ B ^ ) + = A ^ B ^
若要证明某一算符为厄米算符,常用的方法是根据该算符的表达式中已有的厄米算符的性质,对该算符求厄米共轭,证明求厄米共轭后仍为该算符本身。
若算符 A ^ \hat{A} A ^
A ^ + = A ^ − 1 \hat{A}^{+} = \hat{A}^{-1} A ^ + = A ^ − 1
则称 A ^ \hat{A} A ^
例:空间反演算符 P ^ \hat{P} P ^ P ^ + = P ^ \hat{P}^{+} = \hat{P} P ^ + = P ^ P ^ P ^ = I ^ ⟹ P ^ = P ^ − 1 ⟹ P ^ + = P ^ − 1 \hat{P}\hat{P} = \hat{I} \Longrightarrow \hat{P} = \hat{P}^{-1} \Longrightarrow \hat{P}^+ = \hat{P}^{-1} P ^ P ^ = I ^ ⟹ P ^ = P ^ − 1 ⟹ P ^ + = P ^ − 1 P ^ \hat{P} P ^
给定一函数 F ( x ) F(x) F ( x )
F ( x ) = ∑ n = 0 + ∞ F ( n ) ( 0 ) n ! x n F(x) = \sum_{n=0}^{+\infty} \frac{F^{(n)}(0)}{n!} x^n F ( x ) = n = 0 ∑ + ∞ n ! F ( n ) ( 0 ) x n
可以定义算符 A ^ \hat{A} A ^ F ( A ^ ) F(\hat{A}) F ( A ^ )
F ( A ^ ) = ∑ n = 0 + ∞ F ( n ) ( 0 ) n ! A ^ n F(\hat{A}) = \sum_{n=0}^{+\infty} \frac{F^{(n)}(0)}{n!} \hat{A}^n F ( A ^ ) = n = 0 ∑ + ∞ n ! F ( n ) ( 0 ) A ^ n
两个(或多个)算符的函数也可以类似定义,如
F ( A ^ , B ^ ) = ∑ m , n = 0 + ∞ 1 m ! n ! ∂ m + n F ∂ x m ∂ y n ( 0 , 0 ) A ^ m B ^ n F(\hat{A},\hat{B}) = \sum_{m,n=0}^{+\infty} \frac{1}{m!n!} \frac{\partial^{m+n}F}{\partial x^m\partial y^n} (0,0)\ \hat{A}^m\hat{B}^n F ( A ^ , B ^ ) = m , n = 0 ∑ + ∞ m ! n ! 1 ∂ x m ∂ y n ∂ m + n F ( 0 , 0 ) A ^ m B ^ n
定义算符 A ^ , B ^ \hat{A},\hat{B} A ^ , B ^ 对易式 为
[ A ^ , B ^ ] = A ^ B ^ − B ^ A ^ [\hat{A},\hat{B}] = \hat{A}\hat{B} - \hat{B}\hat{A} [ A ^ , B ^ ] = A ^ B ^ − B ^ A ^
若 [ A ^ , B ^ ] = 0 [\hat{A},\hat{B}] = 0 [ A ^ , B ^ ] = 0 A ^ B ^ = B ^ A ^ \hat{A}\hat{B} = \hat{B}\hat{A} A ^ B ^ = B ^ A ^ A ^ \hat{A} A ^ B ^ \hat{B} B ^ 对易 (可交换)。显然一个算符与它本身对易 ,即 [ A ^ , A ^ ] = 0 [\hat{A},\hat{A}] = 0 [ A ^ , A ^ ] = 0
若要计算一个对易式 [ A ^ , B ^ ] [\hat{A},\hat{B}] [ A ^ , B ^ ] [ A ^ , B ^ ] ψ = C ^ ψ ⟹ [ A ^ , B ^ ] = C ^ [\hat{A},\hat{B}]\psi = \hat{C}\psi \Longrightarrow [\hat{A},\hat{B}] = \hat{C} [ A ^ , B ^ ] ψ = C ^ ψ ⟹ [ A ^ , B ^ ] = C ^
[ A ^ , B ^ ] = − [ B ^ , A ^ ] [ A ^ , B ^ + C ^ ] = [ A ^ , B ^ ] + [ A ^ , C ^ ] [ A ^ , B ^ C ^ ] = B ^ [ A ^ , C ^ ] + [ A ^ , B ^ ] C ^ [ A ^ B ^ , C ^ ] = A ^ [ B ^ , C ^ ] + [ A ^ , C ^ ] B ^ [ A ^ , [ B ^ , C ^ ] ] + [ B ^ , [ C ^ , A ^ ] ] + [ C ^ , [ A ^ , B ^ ] ] = 0 \ [\hat{A},\hat{B}] = -[\hat{B},\hat{A}] \ \ [\hat{A},\hat{B}+\hat{C}] = [\hat{A},\hat{B}] + [\hat{A},\hat{C}] \ \ [\hat{A},\hat{B}\hat{C}] = \hat{B}[\hat{A},\hat{C}] + [\hat{A},\hat{B}]\hat{C} \ \ [\hat{A}\hat{B},\hat{C}] = \hat{A}[\hat{B},\hat{C}] + [\hat{A},\hat{C}]\hat{B} \ \ [\hat{A},[\hat{B},\hat{C}]] + [\hat{B},[\hat{C},\hat{A}]] + [\hat{C},[\hat{A},\hat{B}]] = 0 [ A ^ , B ^ ] = − [ B ^ , A ^ ] [ A ^ , B ^ + C ^ ] = [ A ^ , B ^ ] + [ A ^ , C ^ ] [ A ^ , B ^ C ^ ] = B ^ [ A ^ , C ^ ] + [ A ^ , B ^ ] C ^ [ A ^ B ^ , C ^ ] = A ^ [ B ^ , C ^ ] + [ A ^ , C ^ ] B ^ [ A ^ , [ B ^ , C ^ ]] + [ B ^ , [ C ^ , A ^ ]] + [ C ^ , [ A ^ , B ^ ]] = 0
其中最后一个式子称为Jaccobi恒等式。
坐标的各个分量算符之间对易,动量的各个分量算符之间对易。
[ x ^ , y ^ ] = [ x ^ , z ^ ] = [ y ^ , z ^ ] = 0 [ p ^ x , p ^ y ] = [ p ^ x , p ^ z ] = [ p ^ y , p ^ z ] = 0 \ [\hat{x},\hat{y}] = [\hat{x},\hat{z}] = [\hat{y},\hat{z}] = 0 \ \kern 1em \ \ [\hat{p}_x,\hat{p}_y] = [\hat{p}_x,\hat{p}_z] = [\hat{p}_y,\hat{p}_z] = 0 [ x ^ , y ^ ] = [ x ^ , z ^ ] = [ y ^ , z ^ ] = 0 [ p ^ x , p ^ y ] = [ p ^ x , p ^ z ] = [ p ^ y , p ^ z ] = 0
坐标算符与动量算符之间的对易关系为
[ x ^ α , p ^ β ] = i ℏ δ α β ( α , β = x , y , z 或 1 , 2 , 3 ) [\hat{x}{\alpha} , \hat{p} {\beta}] = \mathrm{i} \hbar \delta_{\alpha\beta} \kern 2em (\alpha,\beta = x,y,z 或 1,2,3) [ x ^ α , p ^ β ] = i ℏ δ α β ( α , β = x , y , z 或 1 , 2 , 3 )
分开来看,同分量 的坐标算符与动量算符不对易
[ x ^ , p ^ x ] = [ y ^ , p ^ y ] = [ z ^ , p ^ z ] = i ℏ [\hat{x} , \hat{p}{x}] = [\hat{y} , \hat{p} {y}] = [\hat{z} , \hat{p}_{z}] = \mathrm{i} \hbar [ x ^ , p ^ x ] = [ y ^ , p ^ y ] = [ z ^ , p ^ z ] = i ℏ
不同分量 的坐标算符与动量算符对易
[ x ^ , p ^ y ] = [ x ^ , p ^ z ] = [ y ^ , p ^ x ] = [ y ^ , p ^ z ] = [ z ^ , p ^ x ] = [ z ^ , p ^ y ] = 0 [\hat{x} , \hat{p}{y}] = [\hat{x} , \hat{p} {z}] = [\hat{y} , \hat{p}{x}] = [\hat{y} , \hat{p} {z}] = [\hat{z} , \hat{p}{x}] = [\hat{z} , \hat{p} {y}] = 0 [ x ^ , p ^ y ] = [ x ^ , p ^ z ] = [ y ^ , p ^ x ] = [ y ^ , p ^ z ] = [ z ^ , p ^ x ] = [ z ^ , p ^ y ] = 0
角动量算符三个分量之间的对易关系为
[ L ^ α , L ^ β ] = ε α β γ i ℏ L ^ γ [\hat{L}{\alpha} , \hat{L} {\beta}] = \varepsilon_{\alpha\beta\gamma} \mathrm{i} \hbar \hat{L}_{\gamma} [ L ^ α , L ^ β ] = ε α β γ i ℏ L ^ γ
式中 ε α β γ \varepsilon_{\alpha\beta\gamma} ε α β γ
{ ε α β γ = − ε β α γ = − ε α γ β ε 123 = 1 \begin{cases} \varepsilon_{\alpha\beta\gamma} = - \varepsilon_{\beta\alpha\gamma} = - \varepsilon_{\alpha\gamma\beta} \ \varepsilon_{123} = 1 \end{cases} { ε α β γ = − ε β α γ = − ε α γ β ε 123 = 1
其中 α , β , γ = 1 , 2 , 3 或 x , y , z \alpha,\beta,\gamma=1,2,3或x,y,z α , β , γ = 1 , 2 , 3 或 x , y , z ε α β γ \varepsilon_{\alpha\beta\gamma} ε α β γ ε α β γ = 0 \varepsilon_{\alpha\beta\gamma}=0 ε α β γ = 0
上述的三阶反对称张量可认为表示如下
[ [ 0 0 0 0 0 1 0 − 1 0 ] , [ 0 0 − 1 0 0 0 1 0 0 ] , [ 0 1 0 − 1 0 0 0 0 0 ] ] \begin{bmatrix} \begin{bmatrix} 0 & 0 & 0 \ 0 & 0 & 1 \ 0 & -1 & 0 \end{bmatrix} , \begin{bmatrix} 0 & 0 & -1 \ 0 & 0 & 0 \ 1 & 0 & 0 \end{bmatrix} ,\ \begin{bmatrix} 0 & 1 & 0 \ -1 & 0 & 0 \ 0 & 0 & 0 \end{bmatrix} \end{bmatrix} 0 0 0 0 0 − 1 0 1 0 , 0 0 1 0 0 0 − 1 0 0 , 0 − 1 0 1 0 0 0 0 0
分开来看,不同分量 的角动量算符之间不对易
[ L ^ x , L ^ y ] = i ℏ L ^ z , [ L ^ y , L ^ z ] = i ℏ L ^ x , [ L ^ z , L ^ x ] = i ℏ L ^ y [\hat{L}{x} , \hat{L} {y}] = \mathrm{i} \hbar \hat{L}{z} ,\kern 1em [\hat{L} {y} , \hat{L}{z}] = \mathrm{i} \hbar \hat{L} {x} ,\kern 1em [\hat{L}{z} , \hat{L} {x}] = \mathrm{i} \hbar \hat{L}_{y} [ L ^ x , L ^ y ] = i ℏ L ^ z , [ L ^ y , L ^ z ] = i ℏ L ^ x , [ L ^ z , L ^ x ] = i ℏ L ^ y
可以根据该对易关系拓展角动量算符的定义:若一个矢量算符的三个分量满足上述对易关系,则这个算符就是角动量算符。
角动量算符的三个分量都和角动量的平方对易
[ L ^ x , L ^ 2 ] = [ L ^ y , L ^ 2 ] = [ L ^ z , L ^ 2 ] = 0 [\hat{L}{x} , \hat{L}^2] = [\hat{L} {y} , \hat{L}^2] = [\hat{L}_{z} , \hat{L}^2] = 0 [ L ^ x , L ^ 2 ] = [ L ^ y , L ^ 2 ] = [ L ^ z , L ^ 2 ] = 0
角动量算符与坐标、动量算符之间满足类似于角动量的三个分量之间的对易关系
[ L ^ α , x ^ β ] = ε α β γ i ℏ x ^ γ [ L ^ α , p ^ β ] = ε α β γ i ℏ p ^ γ \ [\hat{L}{\alpha} , \hat{x} {\beta}] = \varepsilon_{\alpha\beta\gamma} \mathrm{i} \hbar \hat{x}{\gamma} \ \kern 1em \ \ [\hat{L} {\alpha} , \hat{p}{\beta}] = \varepsilon {\alpha\beta\gamma} \mathrm{i} \hbar \hat{p}_{\gamma} [ L ^ α , x ^ β ] = ε α β γ i ℏ x ^ γ [ L ^ α , p ^ β ] = ε α β γ i ℏ p ^ γ
分开来看,同分量 的角动量算符与坐标、动量算符对易 ,不同分量 的角动量算符与坐标、动量算符不对易
[ L ^ x , x ^ ] = 0 [ L ^ x , y ^ ] = i ℏ z [ L ^ x , z ^ ] = − i ℏ y [ L ^ y , x ^ ] = − i ℏ z [ L ^ y , y ^ ] = 0 [ L ^ y , z ^ ] = i ℏ x [ L ^ z , x ^ ] = i ℏ y [ L ^ z , y ^ ] = − i ℏ x [ L ^ z , z ^ ] = 0 [ L ^ x , p ^ x ] = 0 [ L ^ x , p ^ y ] = i ℏ p z [ L ^ x , p ^ z ] = − i ℏ p y [ L ^ y , p ^ x ] = − i ℏ p z [ L ^ y , p ^ y ] = 0 [ L ^ y , p ^ z ] = i ℏ p x [ L ^ z , p ^ x ] = i ℏ p y [ L ^ z , p ^ y ] = − i ℏ p x [ L ^ z , p ^ z ] = 0 \begin{matrix} [\hat{L}_x,\hat{x}] = 0 & [\hat{L}_x,\hat{y}] = \mathrm{i}\hbar z & [\hat{L}_x,\hat{z}] = -\mathrm{i}\hbar y \ [\hat{L}_y,\hat{x}] = -\mathrm{i}\hbar z & [\hat{L}_y,\hat{y}] = 0 & [\hat{L}_y,\hat{z}] = \mathrm{i}\hbar x \ [\hat{L}_z,\hat{x}] = \mathrm{i}\hbar y & [\hat{L}_z,\hat{y}] = -\mathrm{i}\hbar x & [\hat{L}_z,\hat{z}] = 0 \end{matrix} \ \kern 1em \ \begin{matrix} [\hat{L}_x,\hat{p}_x] = 0 & [\hat{L}_x,\hat{p}_y] = \mathrm{i}\hbar p_z & [\hat{L}_x,\hat{p}_z] = -\mathrm{i}\hbar p_y \ [\hat{L}_y,\hat{p}_x] = -\mathrm{i}\hbar p_z & [\hat{L}_y,\hat{p}_y] = 0 & [\hat{L}_y,\hat{p}_z] = \mathrm{i}\hbar p_x \ [\hat{L}_z,\hat{p}_x] = \mathrm{i}\hbar p_y & [\hat{L}_z,\hat{p}_y] = -\mathrm{i}\hbar p_x & [\hat{L}_z,\hat{p}_z] = 0 \end{matrix} [ L ^ x , x ^ ] = 0 [ L ^ y , x ^ ] = − i ℏ z [ L ^ z , x ^ ] = i ℏ y [ L ^ x , y ^ ] = i ℏ z [ L ^ y , y ^ ] = 0 [ L ^ z , y ^ ] = − i ℏ x [ L ^ x , z ^ ] = − i ℏ y [ L ^ y , z ^ ] = i ℏ x [ L ^ z , z ^ ] = 0 [ L ^ x , p ^ x ] = 0 [ L ^ y , p ^ x ] = − i ℏ p z [ L ^ z , p ^ x ] = i ℏ p y [ L ^ x , p ^ y ] = i ℏ p z [ L ^ y , p ^ y ] = 0 [ L ^ z , p ^ y ] = − i ℏ p x [ L ^ x , p ^ z ] = − i ℏ p y [ L ^ y , p ^ z ] = i ℏ p x [ L ^ z , p ^ z ] = 0
对于算符 A ^ \hat{A} A ^
A ^ ψ λ = λ ψ λ \hat{A} \psi_{\lambda} = \lambda \psi_{\lambda} A ^ ψ λ = λ ψ λ
算符 A ^ \hat{A} A ^ 本征值 集 { λ } {\lambda} { λ } A A A A ^ \hat{A} A ^ 本征函数 ψ λ \psi_{\lambda} ψ λ A A A λ \lambda λ
本征值可以是分立谱 (discrete spectra)、连续谱 (continuous spectra)和混合谱 。
分立谱的本征值 A n A_n A n
A ^ ψ n = A n ψ n , ( n = 1 , 2 , 3 , ⋯ ) \hat{A} \psi_n = A_n \psi_n\ , \kern 2em (n=1,2,3,\cdots) A ^ ψ n = A n ψ n , ( n = 1 , 2 , 3 , ⋯ )
连续谱的本征值 λ \lambda λ
A ^ ψ λ = λ ψ λ \hat{A} \psi_{\lambda} = \lambda \psi_{\lambda} A ^ ψ λ = λ ψ λ
混合谱是由一部分分立谱与一部分离散谱组成的,如氢原子的能级,在电离前(束缚态)是离散谱,电离后(游离态)是连续谱。
厄米算符的本征值必为实数 。
对于厄米算符 A ^ \hat{A} A ^ λ \lambda λ ψ \psi ψ
A ^ ψ = λ ψ \hat{A} \psi = \lambda \psi A ^ ψ = λ ψ
由厄米算符定义可得
∫ d τ ψ ∗ ( A ^ ψ ) = ∫ d τ ( A ^ ψ ) ∗ ψ ⇓ ∫ d τ ψ ∗ ( λ ψ ) = ∫ d τ ( λ ψ ) ∗ ψ ⇓ λ ∫ d τ ψ ∗ ψ = λ ∗ ∫ d τ ψ ∗ ψ ⇓ λ = λ ∗ \int \mathrm{d}\tau\ \psi^* (\hat{A} \psi) = \int \mathrm{d}\tau\ (\hat{A} \psi)^* \psi \ \Downarrow \ \int \mathrm{d}\tau\ \psi^* (\lambda \psi) = \int \mathrm{d}\tau\ (\lambda \psi)^* \psi \ \Downarrow \ \lambda \int \mathrm{d}\tau\ \psi^* \psi = \lambda^* \int \mathrm{d}\tau\ \psi^* \psi \ \Downarrow \ \lambda = \lambda^* ∫ d τ ψ ∗ ( A ^ ψ ) = ∫ d τ ( A ^ ψ ) ∗ ψ ⇓ ∫ d τ ψ ∗ ( λ ψ ) = ∫ d τ ( λ ψ ) ∗ ψ ⇓ λ ∫ d τ ψ ∗ ψ = λ ∗ ∫ d τ ψ ∗ ψ ⇓ λ = λ ∗
此即表明本征值 λ \lambda λ
体系的任何状态下,其厄米算符的平均值必为实数 ;在任何状态下平均值均为实数 的算符必为厄米算符。即
厄米算符 ⟺ 任何状态下平均值为实数 厄米算符 \Longleftrightarrow 任何状态下平均值为实数 厄米算符 ⟺ 任何状态下平均值为实数
由该定理可知,力学量 即可观测量,当然要求在任何状态下平均值都是实数,所以相应的算符一定是厄米算符 。
⇒ \Rightarrow ⇒
对于厄米算符 A ^ \hat{A} A ^ ψ \psi ψ
A ˉ = ( ψ , A ^ ψ ) = ( A ^ ψ , ψ ) = ( ψ , A ^ ψ ) ∗ = A ˉ ∗ \bar{A} = (\psi,\hat{A}\psi) = (\hat{A}\psi,\psi) = (\psi,\hat{A}\psi)^* = \bar{A}^* A ˉ = ( ψ , A ^ ψ ) = ( A ^ ψ , ψ ) = ( ψ , A ^ ψ ) ∗ = A ˉ ∗
其中第二个等号为厄米算符的性质,第三个等号为内积的性质。
⇐ \Leftarrow ⇐
对于任意已归一化的波函数 ψ \psi ψ A ˉ = A ˉ ∗ \bar{A} = \bar{A}^* A ˉ = A ˉ ∗ A ˉ = ( ψ , A ^ ψ ) \bar{A} = (\psi,\hat{A}\psi) A ˉ = ( ψ , A ^ ψ ) A ˉ ∗ = ( ψ , A ^ ψ ) ∗ = ( A ^ ψ , ψ ) \bar{A}^* = (\psi,\hat{A}\psi)^* = (\hat{A}\psi,\psi) A ˉ ∗ = ( ψ , A ^ ψ ) ∗ = ( A ^ ψ , ψ )
( ψ , A ^ ψ ) = ( A ^ ψ , ψ ) (\psi,\hat{A}\psi) = (\hat{A}\psi,\psi) ( ψ , A ^ ψ ) = ( A ^ ψ , ψ )
注意此时并未完成证明,因为厄米算符的定义是对两个独立的波函数 ψ , φ \psi,\varphi ψ , φ
取任意独立的波函数 ψ 1 , ψ 2 \psi_1,\psi_2 ψ 1 , ψ 2 c c c ψ = ψ 1 + c ψ 2 \psi = \psi_1 + c\psi_2 ψ = ψ 1 + c ψ 2
( ψ , A ^ ψ ) = ( ψ 1 + c ψ 2 , A ^ ( ψ 1 + c ψ 2 ) ) = ( ψ 1 , A ^ ψ 1 ) + c ( ψ 1 , A ^ ψ 2 ) + c ∗ ( ψ 2 , A ^ ψ 1 ) + c ∗ c ( ψ 2 , A ^ ψ 2 ) ( A ^ ψ , ψ ) = ( A ^ ( ψ 1 + c ψ 2 ) , ψ 1 + c ψ 2 ) = ( A ^ ψ 1 , ψ 1 ) + c ( A ^ ψ 1 , ψ 2 ) + c ∗ ( A ^ ψ 2 , ψ 1 ) + c ∗ c ( A ^ ψ 2 , ψ 2 ) (\psi , \hat{A}\psi) = \left(\psi_1 + c\psi_2 , \hat{A}(\psi_1 + c\psi_2)\right) \ = (\psi_1 , \hat{A}\psi_1) + c(\psi_1 , \hat{A}\psi_2) + c^*(\psi_2 , \hat{A}\psi_1) + c^c(\psi_2 , \hat{A}\psi_2) \ \kern 1em \ (\hat{A}\psi,\psi) = \left(\hat{A}(\psi_1 + c\psi_2) , \psi_1 + c\psi_2\right) \ = (\hat{A}\psi_1 , \psi_1) + c(\hat{A}\psi_1 , \psi_2) + c^ (\hat{A}\psi_2 , \psi_1) + c^*c(\hat{A}\psi_2 , \psi_2) ( ψ , A ^ ψ ) = ( ψ 1 + c ψ 2 , A ^ ( ψ 1 + c ψ 2 ) ) = ( ψ 1 , A ^ ψ 1 ) + c ( ψ 1 , A ^ ψ 2 ) + c ∗ ( ψ 2 , A ^ ψ 1 ) + c ∗ c ( ψ 2 , A ^ ψ 2 ) ( A ^ ψ , ψ ) = ( A ^ ( ψ 1 + c ψ 2 ) , ψ 1 + c ψ 2 ) = ( A ^ ψ 1 , ψ 1 ) + c ( A ^ ψ 1 , ψ 2 ) + c ∗ ( A ^ ψ 2 , ψ 1 ) + c ∗ c ( A ^ ψ 2 , ψ 2 )
两组式子应该相等,并利用 ( ψ 1 , A ^ ψ 1 ) = ( A ^ ψ 1 , ψ 1 ) , ( ψ 2 , A ^ ψ 2 ) = ( A ^ ψ 2 , ψ 2 ) (\psi_1,\hat{A}\psi_1) = (\hat{A}\psi_1,\psi_1),\ (\psi_2,\hat{A}\psi_2) = (\hat{A}\psi_2,\psi_2) ( ψ 1 , A ^ ψ 1 ) = ( A ^ ψ 1 , ψ 1 ) , ( ψ 2 , A ^ ψ 2 ) = ( A ^ ψ 2 , ψ 2 )
c ( ψ 1 , A ^ ψ 2 ) + c ∗ ( ψ 2 , A ^ ψ 1 ) = c ( A ^ ψ 1 , ψ 2 ) + c ∗ ( A ^ ψ 2 , ψ 1 ) c(\psi_1 , \hat{A}\psi_2) + c^(\psi_2 , \hat{A}\psi_1) = c(\hat{A}\psi_1 , \psi_2) + c^ (\hat{A}\psi_2 , \psi_1) c ( ψ 1 , A ^ ψ 2 ) + c ∗ ( ψ 2 , A ^ ψ 1 ) = c ( A ^ ψ 1 , ψ 2 ) + c ∗ ( A ^ ψ 2 , ψ 1 )
整理得
c [ ( ψ 1 , A ^ ψ 2 ) − ( A ^ ψ 1 , ψ 2 ) ] = c ∗ [ ( A ^ ψ 2 , ψ 1 ) − ( ψ 2 , A ^ ψ 1 ) ] c\left[(\psi_1 , \hat{A}\psi_2) - (\hat{A}\psi_1 , \psi_2)\right] = c^*\left[(\hat{A}\psi_2 , \psi_1) - (\psi_2 , \hat{A}\psi_1)\right] c [ ( ψ 1 , A ^ ψ 2 ) − ( A ^ ψ 1 , ψ 2 ) ] = c ∗ [ ( A ^ ψ 2 , ψ 1 ) − ( ψ 2 , A ^ ψ 1 ) ]
分别令 c = 1 c=1 c = 1 c = i c=i c = i
( ψ 1 , A ^ ψ 2 ) − ( A ^ ψ 1 , ψ 2 ) = + ( A ^ ψ 2 , ψ 1 ) − ( ψ 2 , A ^ ψ 1 ) ( ψ 1 , A ^ ψ 2 ) − ( A ^ ψ 1 , ψ 2 ) = − ( A ^ ψ 2 , ψ 1 ) + ( ψ 2 , A ^ ψ 1 ) (\psi_1 , \hat{A}\psi_2) - (\hat{A}\psi_1 , \psi_2) = + (\hat{A}\psi_2 , \psi_1) - (\psi_2 , \hat{A}\psi_1) \ \kern 1em \ (\psi_1 , \hat{A}\psi_2) - (\hat{A}\psi_1 , \psi_2) = - (\hat{A}\psi_2 , \psi_1) + (\psi_2 , \hat{A}\psi_1) ( ψ 1 , A ^ ψ 2 ) − ( A ^ ψ 1 , ψ 2 ) = + ( A ^ ψ 2 , ψ 1 ) − ( ψ 2 , A ^ ψ 1 ) ( ψ 1 , A ^ ψ 2 ) − ( A ^ ψ 1 , ψ 2 ) = − ( A ^ ψ 2 , ψ 1 ) + ( ψ 2 , A ^ ψ 1 )
以上两式分别相加、减,即得
( ψ 1 , A ^ ψ 2 ) = ( A ^ ψ 1 , ψ 2 ) , ( A ^ ψ 2 , ψ 1 ) = ( ψ 2 , A ^ ψ 1 ) (\psi_1 , \hat{A}\psi_2) = (\hat{A}\psi_1 , \psi_2), \kern 1em (\hat{A}\psi_2 , \psi_1) = (\psi_2 , \hat{A}\psi_1) ( ψ 1 , A ^ ψ 2 ) = ( A ^ ψ 1 , ψ 2 ) , ( A ^ ψ 2 , ψ 1 ) = ( ψ 2 , A ^ ψ 1 )
此即厄米算符定义的要求。
设 A ^ \hat{A} A ^ ψ \psi ψ
A 2 ˉ = ( ψ , A ^ 2 ψ ) = ( A ^ ψ , A ^ ψ ) ≥ 0 \bar{A^2} = (\psi,\hat{A}^2\psi) = (\hat{A}\psi,\hat{A}\psi) \ge 0 A 2 ˉ = ( ψ , A ^ 2 ψ ) = ( A ^ ψ , A ^ ψ ) ≥ 0
厄米算符的属于不同本征值 的本征函数,彼此正交 。
对于分立谱
( ψ m , ψ n ) = δ m n (\psi_m,\psi_n) = \delta_{mn} ( ψ m , ψ n ) = δ mn
对于连续谱
( ψ λ , ψ λ ′ ) = δ ( λ − λ ′ ) (\psi_{\lambda},\psi_{\lambda'}) = \delta(\lambda-\lambda') ( ψ λ , ψ λ ′ ) = δ ( λ − λ ′ )
连续谱本征函数是不能归一化的,可以使用 δ \delta δ
以分立谱为例证明,连续谱同理。对于厄米算符 A ^ \hat{A} A ^ ψ m , ψ n \psi_m,\psi_n ψ m , ψ n
A ^ ψ n = A n ψ n , A ^ ψ m = A m ψ m \hat{A} \psi_n = A_n \psi_n\ , \kern 2em \hat{A} \psi_m = A_m \psi_m A ^ ψ n = A n ψ n , A ^ ψ m = A m ψ m
并设 ( ψ m , ψ n ) (\psi_m,\psi_n) ( ψ m , ψ n )
A ^ ∗ ψ m ∗ = A m ψ m ∗ \hat{A}^* \psi_m^* = A_m \psi_m^* A ^ ∗ ψ m ∗ = A m ψ m ∗
乘 ψ n \psi_n ψ n
∫ d τ A ^ ∗ ψ m ∗ ψ n = ∫ d τ A m ψ m ∗ ψ n \int \mathrm{d} \tau \hat{A}^* \psi_m^* \psi_n = \int \mathrm{d} \tau A_m \psi_m^* \psi_n ∫ d τ A ^ ∗ ψ m ∗ ψ n = ∫ d τ A m ψ m ∗ ψ n
即
( A ^ ψ m , ψ n ) = A m ( ψ m , ψ n ) (\hat{A}\psi_m,\psi_n) = A_m(\psi_m,\psi_n) ( A ^ ψ m , ψ n ) = A m ( ψ m , ψ n )
由 A ^ \hat{A} A ^ ( A ^ ψ m , ψ n ) = ( ψ m , A ^ ψ n ) = A n ( ψ m , ψ n ) (\hat{A}\psi_m,\psi_n) = (\psi_m,\hat{A}\psi_n) = A_n(\psi_m,\psi_n) ( A ^ ψ m , ψ n ) = ( ψ m , A ^ ψ n ) = A n ( ψ m , ψ n )
( A m − A n ) ( ψ m , ψ n ) = 0 (A_m - A_n) (\psi_m,\psi_n) = 0 ( A m − A n ) ( ψ m , ψ n ) = 0
当 m ≠ n m \ne n m = n A m ≠ A n A_m \ne A_n A m = A n
( ψ m , ψ n ) = 0 (\psi_m,\psi_n) = 0 ( ψ m , ψ n ) = 0
在出现简并态时,简并态的选择不是唯一的,而且选择的简并态不一定彼此正交。但可以证明,总可以把它们适当地线性叠加 ,使之彼此正交 。
这里给出简并态的选择不是唯一的一个例子,对于本征方程 d 2 d x 2 ψ ( x ) + k 2 ψ ( x ) = 0 \frac{\mathrm{d}^2}{\mathrm{d}x^2}\psi(x) + k^2\psi(x) =0 d x 2 d 2 ψ ( x ) + k 2 ψ ( x ) = 0 e ± i k x e^{\pm\mathrm{i}kx} e ± i k x sin x \sin x sin x cos x \cos x cos x sin x + cos x \sin x+\cos x sin x + cos x sin x − cos x \sin x-\cos x sin x − cos x
与线性代数作类比,即选择的子空间的一组基不一定正交,但总可以找到子空间的一组标准正交基(这组正交基也可能不唯一)。
通过正交性定理与该定理,结合后面对完备性的讨论,实际上说明了厄米算符可以选择正交、归一、完备的本征函数系。
设力学量 A A A
A ^ ψ n α = A n ψ n α , ( a = 1 , 2 , ⋯ , f n ) \hat{A} \psi_{n\alpha} = A_n \psi_{n\alpha}\ , \kern 2em (a=1,2,\cdots,f_n) A ^ ψ n α = A n ψ n α , ( a = 1 , 2 , ⋯ , f n )
即属于本征值 A n A_n A n f n f_n f n A n A_n A n f n f_n f n
ϕ n β = ∑ α = 1 f n c β α ψ n α , ( β = 1 , 2 , ⋯ , f n ) \phi_{n\beta} = \sum_{\alpha=1}^{f_n} c_{\beta\alpha} \psi_{n\alpha}\ , \kern 2em (\beta=1,2,\cdots,f_n) ϕ n β = α = 1 ∑ f n c β α ψ n α , ( β = 1 , 2 , ⋯ , f n )
这里得到的 ϕ n β \phi_{n\beta} ϕ n β A ^ \hat{A} A ^ A n A_n A n
A ^ ϕ n β = A ^ ∑ α = 1 f n c β α ψ n α = ∑ α = 1 f n c β α A ^ ψ n α = ∑ α = 1 f n c β α A n ψ n α = A n ∑ α = 1 f n c β α ψ n α = A n ϕ n β \hat{A} \phi_{n\beta} = \hat{A} \sum_{\alpha=1}^{f_n} c_{\beta\alpha} \psi_{n\alpha} = \sum_{\alpha=1}^{f_n} c_{\beta\alpha} \hat{A} \psi_{n\alpha} = \sum_{\alpha=1}^{f_n} c_{\beta\alpha} A_n \psi_{n\alpha} = A_n \sum_{\alpha=1}^{f_n} c_{\beta\alpha} \psi_{n\alpha} = A_n \phi_{n\beta} A ^ ϕ n β = A ^ α = 1 ∑ f n c β α ψ n α = α = 1 ∑ f n c β α A ^ ψ n α = α = 1 ∑ f n c β α A n ψ n α = A n α = 1 ∑ f n c β α ψ n α = A n ϕ n β
可以适当地选择 c β α c_{\beta\alpha} c β α ϕ n β \phi_{n\beta} ϕ n β
( ϕ n β , ϕ n β ′ ) = δ β β ′ (\phi_{n\beta} , \phi_{n\beta'}) = \delta_{\beta\beta'} ( ϕ n β , ϕ n β ′ ) = δ β β ′
对于 f n 2 f_n^2 f n 2 c β α c_{\beta\alpha} c β α 1 2 f n ( f n − 1 ) + f n = 1 2 f n ( f n + 1 ) \frac12f_n(f_n-1)+f_n = \frac12f_n(f_n+1) 2 1 f n ( f n − 1 ) + f n = 2 1 f n ( f n + 1 ) β , β ′ \beta,\beta' β , β ′ C f n 2 = 1 2 f n ( f n − 1 ) C_{f_n}^{2} = \frac12f_n(f_n-1) C f n 2 = 2 1 f n ( f n − 1 ) β , β ′ \beta,\beta' β , β ′ f n f_n f n f n 2 ≥ 1 2 f n ( f n + 1 ) f_n^2 \ge \frac12f_n(f_n+1) f n 2 ≥ 2 1 f n ( f n + 1 ) f n ≥ 2 f_n\ge2 f n ≥ 2
一个函数系完备 ,是指任何一个满足适当边界条件和连续性要求的波函数,均可用这个函数系作展开。
从线性代数的角度来看,就是一组向量可以张成一个子空间,这个子空间中的所有向量都可以用这组向量线性表出。
只有那些本征波函数构成完备系的厄米算符所表达的力学量才是可以观测的,才有物理意义。物理上力学量总是可观测的,所以量子力学有理由认为表达力学量的厄米算符的本征函数系是完备的 。
注:对于常见的势函数体系,其Hamilton量的本征函数系的完备性数学上已经证明,但对任意势函数的情况目前还不能一般地证明。
对于分立谱 :
算符 A ^ \hat{A} A ^ { ψ n } {\psi_n} { ψ n }
A ^ ψ n = A n ψ n , ( n = 1 , 2 , 3 , ⋯ ) \hat{A} \psi_n = A_n \psi_n\ , \kern 2em (n=1,2,3,\cdots) A ^ ψ n = A n ψ n , ( n = 1 , 2 , 3 , ⋯ )
且函数系 { ψ n } {\psi_n} { ψ n } ( ψ m , ψ n ) = δ m n (\psi_m,\psi_n) = \delta_{mn} ( ψ m , ψ n ) = δ mn ϕ \phi ϕ
ϕ ( x ) = ∑ n C n ψ n ( x ) \phi(x) = \sum_{n} C_n\psi_n (x) ϕ ( x ) = n ∑ C n ψ n ( x )
两边同乘 ψ m ∗ \psi_m^* ψ m ∗
∫ d τ ψ m ∗ ϕ = ∫ d τ ψ m ∗ ∑ n C n ψ n = ∑ n C n ∫ d τ ψ m ∗ ψ n = C m \int \mathrm{d}\tau \psi_m^* \phi = \int \mathrm{d}\tau \psi_m^* \sum_{n} C_n\psi_n = \sum_{n}C_n \int \mathrm{d}\tau \psi_m^* \psi_n = C_m ∫ d τ ψ m ∗ ϕ = ∫ d τ ψ m ∗ n ∑ C n ψ n = n ∑ C n ∫ d τ ψ m ∗ ψ n = C m
由此可以求出展开式的系数
C n = ( ψ n , ϕ ) = ∫ d τ ψ n ∗ ϕ C_n = (\psi_n,\phi) = \int \mathrm{d}\tau \psi_n^* \phi C n = ( ψ n , ϕ ) = ∫ d τ ψ n ∗ ϕ
展开系数 C n C_n C n ϕ \phi ϕ ψ n \psi_n ψ n
Φ = [ C 1 C 2 ⋮ ] \Phi = \begin{bmatrix} C_1 \ C_2 \ \vdots \end{bmatrix} Φ = C 1 C 2 ⋮
代表态矢 ϕ \phi ϕ { ψ n } { \psi_n } { ψ n } A ^ \hat{A} A ^
对于连续谱 :
算符 A ^ \hat{A} A ^ { ψ λ } {\psi_{\lambda}} { ψ λ }
A ^ ψ λ = λ ψ λ , ( n = 1 , 2 , 3 , ⋯ ) \hat{A} \psi_\lambda = \lambda \psi_\lambda\ , \kern 2em (n=1,2,3,\cdots) A ^ ψ λ = λ ψ λ , ( n = 1 , 2 , 3 , ⋯ )
且函数系 { ψ λ } {\psi_\lambda} { ψ λ } ( ψ λ , ψ λ ′ ) = δ ( λ − λ ′ ) (\psi_{\lambda},\psi_{\lambda'}) = \delta(\lambda-\lambda') ( ψ λ , ψ λ ′ ) = δ ( λ − λ ′ ) ϕ \phi ϕ
φ ( x ) = ∫ C ( λ ) ψ λ ( x ) d λ \varphi(x) = \int C(\lambda) \psi_\lambda (x) \mathrm{d}\lambda φ ( x ) = ∫ C ( λ ) ψ λ ( x ) d λ
两边同乘 ψ λ ′ ∗ \psi_{\lambda'}^* ψ λ ′ ∗
∫ d τ ψ λ ′ ∗ ϕ = ∫ d τ ψ λ ′ ∗ ∫ C ( λ ) ψ λ d λ = ∫ d λ C ( λ ) ∫ d τ ψ λ ′ ∗ ψ λ = ∫ d λ C ( λ ) δ ( λ − λ ′ ) = C ( λ ′ ) \int \mathrm{d}\tau \psi_{\lambda'}^* \phi = \int \mathrm{d}\tau \psi_{\lambda'}^* \int C(\lambda) \psi_\lambda \mathrm{d}\lambda = \int \mathrm{d}\lambda C(\lambda) \int \mathrm{d}\tau \psi_{\lambda'}^* \psi_{\lambda} = \int \mathrm{d}\lambda C(\lambda) \delta(\lambda-\lambda') = C(\lambda') ∫ d τ ψ λ ′ ∗ ϕ = ∫ d τ ψ λ ′ ∗ ∫ C ( λ ) ψ λ d λ = ∫ d λ C ( λ ) ∫ d τ ψ λ ′ ∗ ψ λ = ∫ d λ C ( λ ) δ ( λ − λ ′ ) = C ( λ ′ )
由此可以求出展开式的系数
C ( λ ) = ( ψ λ , ϕ ) = ∫ d τ ψ λ ∗ ϕ C(\lambda) = (\psi_\lambda,\phi) = \int \mathrm{d}\tau \psi_\lambda^* \phi C ( λ ) = ( ψ λ , ϕ ) = ∫ d τ ψ λ ∗ ϕ
对于分立谱,本征函数系 { ψ n } { \psi_n } { ψ n } 封闭关系
∑ n ψ n ∗ ( x ′ ) ψ n ( x ) = δ ( x ′ − x ) \sum_{n} \psi_n^*(x')\ \psi_n(x) = \delta(x'-x) n ∑ ψ n ∗ ( x ′ ) ψ n ( x ) = δ ( x ′ − x )
对于连续谱,本征函数系 { ψ λ } { \psi_\lambda } { ψ λ } 封闭关系
∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ = δ ( x ′ − x ) \int \psi_\lambda^*(x')\ \psi_\lambda(x)\ \mathrm{d}\lambda = \delta(x'-x) ∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ = δ ( x ′ − x )
对于分立谱 :
若本征函数系 { ψ n } { \psi_n } { ψ n } ϕ ( x ) \phi(x) ϕ ( x )
ϕ ( x ) = ∑ n C n ψ n ( x ) = ∑ n [ ∫ − ∞ + ∞ ψ n ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ n ( x ) = ∫ − ∞ + ∞ ϕ ( x ′ ) [ ∑ n ψ n ∗ ( x ′ ) ψ n ( x ) ] d x ′ \phi (x) = \sum_n C_n \psi_n(x) = \sum_n \left[ \int_{-\infty}^{+\infty} \psi_n^(x') \phi(x') \mathrm{d}x' \right] \psi_n(x) = \int_{-\infty}^{+\infty} \phi(x') \left[ \sum_n \psi_n^ (x') \psi_n(x) \right] \mathrm{d}x' ϕ ( x ) = n ∑ C n ψ n ( x ) = n ∑ [ ∫ − ∞ + ∞ ψ n ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ n ( x ) = ∫ − ∞ + ∞ ϕ ( x ′ ) [ n ∑ ψ n ∗ ( x ′ ) ψ n ( x ) ] d x ′
通过上述积分式可以得到
∑ n ψ n ∗ ( x ′ ) ψ n ( x ) = δ ( x ′ − x ) \sum_n \psi_n^*(x') \psi_n(x) = \delta(x'-x) n ∑ ψ n ∗ ( x ′ ) ψ n ( x ) = δ ( x ′ − x )
而若本征函数系 { ψ n } { \psi_n } { ψ n }
ϕ ( x ) = ∫ − ∞ + ∞ ϕ ( x ′ ) δ ( x ′ − x ) d x ′ = ∫ − ∞ + ∞ ϕ ( x ′ ) [ ∑ n ψ n ∗ ( x ′ ) ψ n ( x ) ] d x ′ = ∑ n [ ∫ − ∞ + ∞ ψ n ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ n ( x ) \phi (x) = \int_{-\infty}^{+\infty} \phi(x') \delta(x'-x) \mathrm{d}x' = \int_{-\infty}^{+\infty} \phi(x') \left[ \sum_n \psi_n^(x') \psi_n(x) \right] \mathrm{d}x' = \sum_n \left[ \int_{-\infty}^{+\infty} \psi_n^ (x') \phi(x') \mathrm{d}x' \right] \psi_n(x) ϕ ( x ) = ∫ − ∞ + ∞ ϕ ( x ′ ) δ ( x ′ − x ) d x ′ = ∫ − ∞ + ∞ ϕ ( x ′ ) [ n ∑ ψ n ∗ ( x ′ ) ψ n ( x ) ] d x ′ = n ∑ [ ∫ − ∞ + ∞ ψ n ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ n ( x )
这就表现为任意波函数 ϕ ( x ) \phi(x) ϕ ( x ) { ψ n } { \psi_n } { ψ n } { ψ n } { \psi_n } { ψ n }
对于连续谱 :
若本征函数系 { ψ λ } { \psi_\lambda } { ψ λ } ϕ ( x ) \phi(x) ϕ ( x )
ϕ ( x ) = ∫ C ( λ ) ψ λ ( x ) d λ = ∫ [ ∫ − ∞ + ∞ ψ λ ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ λ ( x ) d λ = ∫ − ∞ + ∞ ϕ ( x ′ ) [ ∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ ] d x ′ \phi (x) = \int C(\lambda) \psi_\lambda(x) \mathrm{d}\lambda = \int \left[ \int_{-\infty}^{+\infty} \psi_\lambda^(x') \phi(x') \mathrm{d}x' \right] \psi_\lambda(x) \mathrm{d}\lambda = \int_{-\infty}^{+\infty} \phi(x') \left[ \int \psi_\lambda^ (x') \psi_\lambda(x) \mathrm{d}\lambda \right] \mathrm{d}x' ϕ ( x ) = ∫ C ( λ ) ψ λ ( x ) d λ = ∫ [ ∫ − ∞ + ∞ ψ λ ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ λ ( x ) d λ = ∫ − ∞ + ∞ ϕ ( x ′ ) [ ∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ ] d x ′
通过上述积分式可以得到
∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ = δ ( x ′ − x ) \int \psi_\lambda^*(x') \psi_\lambda(x) \mathrm{d}\lambda = \delta(x'-x) ∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ = δ ( x ′ − x )
而若本征函数系 { ψ λ } { \psi_\lambda } { ψ λ }
ϕ ( x ) = ∫ − ∞ + ∞ ϕ ( x ′ ) δ ( x ′ − x ) d x ′ = ∫ − ∞ + ∞ ϕ ( x ′ ) [ ∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ ] d x ′ = ∫ [ ∫ − ∞ + ∞ ψ λ ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ λ ( x ) d λ \phi (x) = \int_{-\infty}^{+\infty} \phi(x') \delta(x'-x) \mathrm{d}x' = \int_{-\infty}^{+\infty} \phi(x') \left[ \int \psi_\lambda^(x') \psi_\lambda(x) \mathrm{d}\lambda \right] \mathrm{d}x' = \int \left[ \int_{-\infty}^{+\infty} \psi_\lambda^ (x') \phi(x') \mathrm{d}x' \right] \psi_\lambda(x) \mathrm{d}\lambda ϕ ( x ) = ∫ − ∞ + ∞ ϕ ( x ′ ) δ ( x ′ − x ) d x ′ = ∫ − ∞ + ∞ ϕ ( x ′ ) [ ∫ ψ λ ∗ ( x ′ ) ψ λ ( x ) d λ ] d x ′ = ∫ [ ∫ − ∞ + ∞ ψ λ ∗ ( x ′ ) ϕ ( x ′ ) d x ′ ] ψ λ ( x ) d λ
这就表现为任意波函数 ϕ ( x ) \phi(x) ϕ ( x ) { ψ λ } { \psi_\lambda } { ψ λ } { ψ λ } { \psi_\lambda } { ψ λ }
这里是课本上关于力学量与算符关系的总结部分,同时补充了课件上关于力学量的平均值部分。
量子力学中力学量 用相应的线性的厄米算符 来表达,其有以下多个含义:
在给定状态 ψ \psi ψ A A A A ˉ \bar{A} A ˉ
A ˉ = ( ψ , A ^ ψ ) ( ψ , ψ ) \bar{A} = \frac{(\psi,\hat{A}\psi)}{(\psi,\psi)} A ˉ = ( ψ , ψ ) ( ψ , A ^ ψ )
这里直接给出混合谱 的计算方式,分立谱与连续谱的计算方式均可从中取出一部分得到。设
ψ ( x ) = ∑ n C n ψ n ( x ) + ∫ C ( λ ) ψ λ d λ \psi(x) = \sum_n C_n\psi_n(x) + \int C(\lambda) \psi_\lambda \mathrm{d}\lambda ψ ( x ) = n ∑ C n ψ n ( x ) + ∫ C ( λ ) ψ λ d λ
其中
C n = ( ψ n , ψ ) , C ( λ ) = ( ψ λ , ψ ) ∑ n ∣ C n ∣ 2 + ∫ ∣ C ( λ ) ∣ 2 d λ = 1 C_n = (\psi_n,\psi) \ , \kern 1em C(\lambda) = (\psi_\lambda,\psi) \ \ \ \sum_n \left|C_n\right|^2 + \int \left|C(\lambda)\right|^2 \mathrm{d}\lambda = 1 C n = ( ψ n , ψ ) , C ( λ ) = ( ψ λ , ψ ) n ∑ ∣ C n ∣ 2 + ∫ ∣ C ( λ ) ∣ 2 d λ = 1
设
A ^ ψ n = A n ψ n , A ^ ψ λ = λ ψ λ \hat{A} \psi_n = A_n \psi_n \ , \kern 1em \hat{A} \psi_\lambda = \lambda \psi_\lambda A ^ ψ n = A n ψ n , A ^ ψ λ = λ ψ λ
则在状态 ψ \psi ψ A A A
A ˉ = ∑ n A n ∣ C n ∣ 2 + ∫ λ ∣ C ( λ ) ∣ 2 d λ \bar{A} = \sum_{n} A_n |C_n|^2 + \int \lambda |C(\lambda)|^2 \mathrm{d}\lambda A ˉ = n ∑ A n ∣ C n ∣ 2 + ∫ λ ∣ C ( λ ) ∣ 2 d λ
在实验上观测某力学量 A A A A ^ \hat{A} A ^
力学量之间的关系也通过相应的算符之间的关系反映出来。例如,两个力学量 A A A B B B [ A ^ , B ^ ] = 0 [\hat{A},\hat{B}] = 0 [ A ^ , B ^ ] = 0 [ A ^ , B ^ ] ≠ 0 [\hat{A},\hat{B}] \ne 0 [ A ^ , B ^ ] = 0 A A A B B B
若波函数 ψ \psi ψ A ^ , B ^ , ⋯ \hat{A},\hat{B},\cdots A ^ , B ^ , ⋯
A ^ ψ = λ ψ , B ^ ψ = μ ψ , ⋯ \hat{A} \psi = \lambda \psi \ , \kern 1em \hat{B}\psi = \mu \psi \ , \kern 1em \cdots A ^ ψ = λ ψ , B ^ ψ = μ ψ , ⋯
则称 ψ \psi ψ A ^ , B ^ , ⋯ \hat{A},\hat{B},\cdots A ^ , B ^ , ⋯ 共同本征函数 (同时本征函数),也称为共同本征态。
如果算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 共同本征函数 { ψ n } { \psi_n } { ψ n } { ψ n } { \psi_n } { ψ n } 完备 系,则算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 对易 。(连续谱同)
如果算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 对易 ,则 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 共同本征函数 ,即存在 ψ \psi ψ A ^ ψ = λ ψ \hat{A}\psi = \lambda\psi A ^ ψ = λ ψ B ^ ψ = μ ψ \hat{B}\psi = \mu\psi B ^ ψ = μ ψ
要注意第二句话中是存在 共同本征函数,也就是不意味着两个算符具有相同的共同本征函数系(二者的简并度甚至都一定不相同),也就是不意味着算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^
第二句话反过来说,如果算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 不对易 ,则一般 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 没有共同本征函数 ,即不能共同测定,这是不确定度关系的表现。
设
A ^ ψ n = A n ψ n , B ^ ψ n = B n ψ n \hat{A} \psi_n = A_n \psi_n \ , \kern 1em \hat{B} \psi_n = B_n \psi_n A ^ ψ n = A n ψ n , B ^ ψ n = B n ψ n
则
( A ^ B ^ − B ^ A ^ ) ψ n = A ^ ( B n ψ n ) − B ^ ( A n ψ n ) = B n ( A ^ ψ n ) − A n ( B ^ ψ n ) = B n A n ψ n − A n B n ψ n = 0 (\hat{A}\hat{B}-\hat{B}\hat{A}) \psi_n = \hat{A}(B_n\psi_n) - \hat{B}(A_n\psi_n) = B_n(\hat{A}\psi_n) - A_n(\hat{B}\psi_n) = B_nA_n\psi_n - A_nB_n\psi_n = 0 ( A ^ B ^ − B ^ A ^ ) ψ n = A ^ ( B n ψ n ) − B ^ ( A n ψ n ) = B n ( A ^ ψ n ) − A n ( B ^ ψ n ) = B n A n ψ n − A n B n ψ n = 0
设 ψ \psi ψ 任意 波函数,由于 { ψ n } { \psi_n } { ψ n } ψ \psi ψ { ψ n } { \psi_n } { ψ n }
ψ = ∑ n C n ψ n \psi = \sum_n C_n \psi_n ψ = n ∑ C n ψ n
故
( A ^ B ^ − B ^ A ^ ) ψ = ( A ^ B ^ − B ^ A ^ ) ∑ n C n ψ n = ∑ n C n ( A ^ B ^ − B ^ A ^ ) ψ n = 0 (\hat{A}\hat{B}-\hat{B}\hat{A}) \psi = (\hat{A}\hat{B}-\hat{B}\hat{A}) \sum_n C_n\psi_n = \sum_n C_n (\hat{A}\hat{B}-\hat{B}\hat{A}) \psi_n = 0 ( A ^ B ^ − B ^ A ^ ) ψ = ( A ^ B ^ − B ^ A ^ ) n ∑ C n ψ n = n ∑ C n ( A ^ B ^ − B ^ A ^ ) ψ n = 0
此即说明了
[ A ^ , B ^ ] = 0 [\hat{A},\hat{B}] = 0 [ A ^ , B ^ ] = 0
假设算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 非简并 的本征值,不妨设 A ^ \hat{A} A ^ λ n \lambda_n λ n
A ^ ψ n = λ n ψ n \hat{A} \psi_n = \lambda_n \psi_n A ^ ψ n = λ n ψ n
由 A ^ \hat{A} A ^ B ^ \hat{B} B ^ A ^ \hat{A} A ^ B ^ \hat{B} B ^
A ^ B ^ ψ n = B ^ A ^ ψ n = B ^ ( λ n ψ n ) = λ n B ^ ψ n \hat{A} \hat{B} \psi_n = \hat{B} \hat{A} \psi_n = \hat{B} (\lambda_n \psi_n) = \lambda_n \hat{B} \psi_n A ^ B ^ ψ n = B ^ A ^ ψ n = B ^ ( λ n ψ n ) = λ n B ^ ψ n
由 A ^ ( B ^ ψ n ) = λ n ( B ^ ψ n ) \hat{A}(\hat{B}\psi_n) = \lambda_n (\hat{B}\psi_n) A ^ ( B ^ ψ n ) = λ n ( B ^ ψ n ) B ^ ψ n \hat{B}\psi_n B ^ ψ n A ^ \hat{A} A ^ λ n \lambda_n λ n A ^ \hat{A} A ^ λ n \lambda_n λ n ψ n \psi_n ψ n
B ^ ψ n = μ n ψ n \hat{B}\psi_n = \mu_n \psi_n B ^ ψ n = μ n ψ n
即 ψ n \psi_n ψ n B ^ \hat{B} B ^ ψ n \psi_n ψ n A ^ \hat{A} A ^ B ^ \hat{B} B ^
而若算符 A ^ \hat{A} A ^ B ^ \hat{B} B ^ 简并 的,不妨设算符 A ^ \hat{A} A ^ λ n \lambda_n λ n f n f_n f n ψ n 1 , ψ n 2 , ⋯ , ψ n f n \psi_{n1},\psi_{n2},\cdots,\psi_{nf_n} ψ n 1 , ψ n 2 , ⋯ , ψ n f n A ^ ψ n α = λ n ψ n α ( α = 1 , 2 , ⋯ , f n ) \hat{A} \psi_{n\alpha} = \lambda_n \psi_{n\alpha} \kern 1em (\alpha=1,2,\cdots,f_n) A ^ ψ n α = λ n ψ n α ( α = 1 , 2 , ⋯ , f n ) A ^ \hat{A} A ^ B ^ \hat{B} B ^
A ^ B ^ ψ n α = B ^ A ^ ψ n α = B ^ ( λ n ψ n α ) = λ n B ^ ψ n α \hat{A} \hat{B} \psi_{n\alpha} = \hat{B} \hat{A} \psi_{n\alpha} = \hat{B} (\lambda_n\psi_{n\alpha}) = \lambda_n \hat{B} \psi_{n\alpha} A ^ B ^ ψ n α = B ^ A ^ ψ n α = B ^ ( λ n ψ n α ) = λ n B ^ ψ n α
由 A ^ ( B ^ ψ n α ) = λ n ( B ^ ψ n α ) \hat{A}(\hat{B}\psi_{n\alpha}) = \lambda_n (\hat{B}\psi_{n\alpha}) A ^ ( B ^ ψ n α ) = λ n ( B ^ ψ n α ) ψ n α \psi_{n\alpha} ψ n α B ^ \hat{B} B ^ B ^ ψ n α \hat{B}\psi_{n\alpha} B ^ ψ n α { ψ n 1 , ψ n 2 , ⋯ , ψ n f n } { \psi_{n1},\psi_{n2},\cdots,\psi_{nf_n} } { ψ n 1 , ψ n 2 , ⋯ , ψ n f n }
B ^ ψ n α = ∑ β = 1 f n μ α β ψ n β \hat{B} \psi_{n\alpha} = \sum_{\beta=1}^{f_n} \mu_{\alpha\beta} \psi_{n\beta} B ^ ψ n α = β = 1 ∑ f n μ α β ψ n β
(根据“在完备函数系下的展开”)其中 μ α β = ( ψ n β , B ^ ψ n α ) \mu_{\alpha\beta} = (\psi_{n\beta},\hat{B}\psi_{n\alpha}) μ α β = ( ψ n β , B ^ ψ n α ) ϕ \phi ϕ A ^ \hat{A} A ^ B ^ \hat{B} B ^
ϕ = ∑ α = 1 f n C α ψ n α \phi = \sum_{\alpha=1}^{f_n} C_\alpha \psi_{n\alpha} ϕ = α = 1 ∑ f n C α ψ n α
则
A ^ ϕ = A ^ ( ∑ α = 1 f n C α ψ n α ) = ∑ α = 1 f n C α A ^ ψ n α = ∑ α = 1 f n C α λ n ψ n α = λ n ( ∑ α = 1 f n C α ψ n α ) = λ n ϕ \hat{A} \phi = \hat{A} \left( \sum_{\alpha=1}^{f_n} C_\alpha \psi_{n\alpha} \right) = \sum_{\alpha=1}^{f_n} C_\alpha \hat{A} \psi_{n\alpha} = \sum_{\alpha=1}^{f_n} C_\alpha \lambda_n \psi_{n\alpha} = \lambda_n \left( \sum_{\alpha=1}^{f_n} C_\alpha \psi_{n\alpha} \right) = \lambda_n \phi A ^ ϕ = A ^ ( α = 1 ∑ f n C α ψ n α ) = α = 1 ∑ f n C α A ^ ψ n α = α = 1 ∑ f n C α λ n ψ n α = λ n ( α = 1 ∑ f n C α ψ n α ) = λ n ϕ
即 ϕ \phi ϕ A ^ \hat{A} A ^
B ^ ϕ = B ^ ( ∑ α = 1 f n C α ψ n α ) = ∑ α = 1 f n C α B ^ ψ n α = ∑ α = 1 f n C α ( ∑ β = 1 f n μ α β ψ n β ) = ∑ β = 1 f n ( ∑ α = 1 f n C α μ α β ) ψ n β \hat{B} \phi = \hat{B} \left( \sum_{\alpha=1}^{f_n} C_\alpha \psi_{n\alpha} \right) = \sum_{\alpha=1}^{f_n} C_\alpha \hat{B} \psi_{n\alpha} = \sum_{\alpha=1}^{f_n} C_\alpha \left( \sum_{\beta=1}^{f_n} \mu_{\alpha\beta} \psi_{n\beta} \right) = \sum_{\beta=1}^{f_n} \left( \sum_{\alpha=1}^{f_n} C_\alpha \mu_{\alpha\beta} \right) \psi_{n\beta} B ^ ϕ = B ^ ( α = 1 ∑ f n C α ψ n α ) = α = 1 ∑ f n C α B ^ ψ n α = α = 1 ∑ f n C α β = 1 ∑ f n μ α β ψ n β = β = 1 ∑ f n ( α = 1 ∑ f n C α μ α β ) ψ n β
如果想要 ϕ \phi ϕ B ^ \hat{B} B ^
B ^ ϕ = μ ϕ = μ ∑ α = 1 f n C α ψ n α = ∑ β = 1 f n C β μ ψ n β \hat{B} \phi = \mu \phi = \mu \sum_{\alpha=1}^{f_n} C_\alpha \psi_{n\alpha} = \sum_{\beta=1}^{f_n} C_\beta \mu \ \psi_{n\beta} B ^ ϕ = μ ϕ = μ α = 1 ∑ f n C α ψ n α = β = 1 ∑ f n C β μ ψ n β
将两个式子对比,使得每一个 ψ n β \psi_{n\beta} ψ n β
∑ α = 1 f n C α μ α β = C β μ ⟹ ∑ α = 1 f n ( μ α β − μ δ α β ) C α = 0 \sum_{\alpha=1}^{f_n} C_\alpha \mu_{\alpha\beta} = C_\beta \mu \Longrightarrow \sum_{\alpha=1}^{f_n} \left( \mu_{\alpha\beta} - \mu \delta_{\alpha\beta} \right) C_\alpha = 0 α = 1 ∑ f n C α μ α β = C β μ ⟹ α = 1 ∑ f n ( μ α β − μ δ α β ) C α = 0
对于 f n f_n f n β \beta β C α ( α = 1 , 2 , ⋯ , f n ) C_\alpha \ (\alpha=1,2,\cdots,f_n) C α ( α = 1 , 2 , ⋯ , f n ) C α C_\alpha C α
det ( [ μ α β − μ δ α β ] f n × f n ) = 0 \det\left( \begin{bmatrix} \mu_{\alpha\beta} - \mu \delta_{\alpha\beta} \end{bmatrix} _{f_n \times f_n}\right) = 0 det ( [ μ α β − μ δ α β ] f n × f n ) = 0
这是一个关于 μ \mu μ f n f_n f n μ \mu μ f n f_n f n C α C_\alpha C α ϕ \phi ϕ A ^ \hat{A} A ^ B ^ \hat{B} B ^
事实上,对于上述行列式,可以化为 det ( [ μ α β ] f n × f n − μ I f n ) = 0 \det\left( \begin{bmatrix} \mu_{\alpha\beta} \end{bmatrix}{f_n \times f_n} - \mu I {f_n} \right) = 0 det ( [ μ α β ] f n × f n − μ I f n ) = 0 μ \mu μ [ μ α β ] f n × f n \begin{bmatrix} \mu_{\alpha\beta} \end{bmatrix}{f {n} \times f_{n}} [ μ α β ] f n × f n C α C_\alpha C α [ μ α β ] f n × f n \begin{bmatrix} \mu_{\alpha\beta} \end{bmatrix}{f {n} \times f_{n}} [ μ α β ] f n × f n
通过算符函数的定义(展开式),不难发现算符 A ^ \hat{A} A ^ F ( A ^ ) F(\hat{A}) F ( A ^ ) A ^ \hat{A} A ^ A ^ ψ λ = λ ψ λ \hat{A} \psi_{\lambda} = \lambda \psi_{\lambda} A ^ ψ λ = λ ψ λ F ( A ^ ) F(\hat{A}) F ( A ^ )
F ( A ^ ) ψ λ = F ( λ ) ψ λ F(\hat{A}) \psi_{\lambda} = F(\lambda) \psi_{\lambda} F ( A ^ ) ψ λ = F ( λ ) ψ λ
即本征值为 F ( λ ) F(\lambda) F ( λ ) ψ λ \psi_{\lambda} ψ λ
设有一组彼此独立 而且互相对易 的厄米算符 A ^ 1 , A ^ 2 , ⋯ \hat{A}{1},\hat{A} {2},\cdots A ^ 1 , A ^ 2 , ⋯ ψ α \psi_{\alpha} ψ α α \alpha α 一组完备 的量子数。设给定一组量子数 α \alpha α 唯一 一个可能状态,则称 A ^ 1 , A ^ 2 , ⋯ \hat{A}_1,\hat{A}_2,\cdots A ^ 1 , A ^ 2 , ⋯ 对易力学量完全集 (complete set of commuting observables,简记为CSCO),也称为对易可观测量完全集 ,或简称为力学量完全集 。也可以说:力学量完全集指的是互相对易 的能够对一个量子体系全部状态进行彻底(不出现简并)地分类标记的最少数目 的力学量算符。
对于此定义,可以这么理解:对于本征方程 A ^ ψ = λ ψ \hat{A} \psi = \lambda \psi A ^ ψ = λ ψ λ \lambda λ λ \lambda λ λ \lambda λ ψ \psi ψ A ^ \hat{A} A ^ λ \lambda λ ψ \psi ψ ν , l , j \nu,l,j ν , l , j
算符为
{ x ^ , y ^ , z ^ } { \hat{x},\hat{y},\hat{z} } { x ^ , y ^ , z ^ }
共同本征函数系为
ψ x 0 , y 0 , z 0 ( x , y , z ) = δ ( x − x 0 ) δ ( y − y 0 ) δ ( z − z 0 ) \psi_{x_0,y_0,z_0} (x,y,z) = \delta(x-x_0) \delta(y-y_0) \delta(z-z_0) ψ x 0 , y 0 , z 0 ( x , y , z ) = δ ( x − x 0 ) δ ( y − y 0 ) δ ( z − z 0 )
相应的本征值为
{ x 0 , y 0 , z 0 } { x_0,y_0,z_0 } { x 0 , y 0 , z 0 }
算符为
{ p ^ x , p ^ y , p ^ z } { \hat{p}_x,\hat{p}_y,\hat{p}_z } { p ^ x , p ^ y , p ^ z }
共同本征函数系为
ψ p x , p y , p z ( x , y , z ) = 1 ( 2 π ℏ ) 3 2 exp [ i ℏ ( p x x + p y y + p z z ) ] \psi_{p_x,p_y,p_z} (x,y,z) = \frac{1}{(2\pi\hbar)^{\frac32}} \exp \left[ \frac{\mathrm{i}}{\hbar} (p_xx+p_yy+p_zz) \right] ψ p x , p y , p z ( x , y , z ) = ( 2 π ℏ ) 2 3 1 exp [ ℏ i ( p x x + p y y + p z z ) ]
相应的本征值为
{ p x , p y , p z } { p_x,p_y,p_z } { p x , p y , p z }
算符为
{ L ^ 2 , L ^ z } { \hat{L}^2,\hat{L}_z } { L ^ 2 , L ^ z }
在球坐标系下,算符 L ^ 2 \hat{L}^2 L ^ 2 L ^ z \hat{L}_z L ^ z
Y l m ( θ , φ ) = ( − 1 ) m 2 l + 1 4 π ( l − m ) ! ( l + m ) ! P l m ( cos θ ) e i m φ \mathrm{Y}_{lm} (\theta,\varphi) = (-1)^m \sqrt{\frac{2l+1}{4\pi} \frac{(l-m)!}{(l+m)!}}\ \mathrm{P}_l^m (\cos\theta)\ \mathrm{e}^{\mathrm{i}m\varphi} Y l m ( θ , φ ) = ( − 1 ) m 4 π 2 l + 1 ( l + m )! ( l − m )! P l m ( cos θ ) e i m φ
式中 Y l m Y_{lm} Y l m 球谐函数 , P l m P_l^m P l m 连带Legendre多项式 。
算符 L ^ 2 \hat{L}^2 L ^ 2 L ^ z \hat{L}_z L ^ z l l l 轨道角动量量子数 ,可以取 l = 0 , 1 , 2 , 3 , ⋯ l=0,1,2,3,\cdots l = 0 , 1 , 2 , 3 , ⋯ s , p , d , f , ⋯ s,p,d,f,\cdots s , p , d , f , ⋯ m m m 磁量子数 ,可以取 m = l , l − 1 , ⋯ , − l + 1 , − l m=l,l-1,\cdots,-l+1,-l m = l , l − 1 , ⋯ , − l + 1 , − l L ^ z \hat{L}_z L ^ z m ℏ m\hbar m ℏ L ^ 2 \hat{L}^2 L ^ 2 l ( l + 1 ) ℏ 2 l(l+1)\hbar^2 l ( l + 1 ) ℏ 2
只考虑算符 L ^ 2 \hat{L}^2 L ^ 2 l l l ( 2 l + 1 ) (2l+1) ( 2 l + 1 ) L ^ z \hat{L}_z L ^ z m m m L ^ 2 \hat{L}^2 L ^ 2 L ^ z \hat{L}_z L ^ z
球坐标下角动量 z z z L ^ z = − i ℏ ∂ ∂ φ \hat{L}_z = -\mathrm{i}\hbar\frac{\partial}{\partial\varphi} L ^ z = − i ℏ ∂ φ ∂
− i ℏ ∂ ∂ φ ψ = L z ψ -\mathrm{i}\hbar\frac{\partial}{\partial\varphi} \psi = L_z \psi − i ℏ ∂ φ ∂ ψ = L z ψ
解得
ψ ( φ ) = C e i ℏ L z φ \psi(\varphi) = C \mathrm{e}^{\frac{\mathrm{i}}{\hbar}L_z\varphi} ψ ( φ ) = C e ℏ i L z φ
为保证算符 L ^ z \hat{L}_z L ^ z ψ \psi ψ 周期性边界条件
ψ ( φ + 2 π ) = ψ ( φ ) \psi(\varphi + 2\pi) = \psi(\varphi) ψ ( φ + 2 π ) = ψ ( φ )
由此条件可得
C e i ℏ L z ( φ + 2 π ) = C e i ℏ L z ( φ ) ⟹ e i ℏ 2 π L z = 1 ⟹ 2 π L z ℏ = 2 m π ⟹ L z = m ℏ C \mathrm{e}^{\frac{\mathrm{i}}{\hbar}L_z(\varphi+2\pi)} = C \mathrm{e}^{\frac{\mathrm{i}}{\hbar}L_z(\varphi)} \Longrightarrow \mathrm{e}^{\frac{\mathrm{i}}{\hbar}2\pi L_z} = 1 \Longrightarrow \frac{2\pi L_z}{\hbar} = 2m\pi \Longrightarrow L_z = m\hbar C e ℏ i L z ( φ + 2 π ) = C e ℏ i L z ( φ ) ⟹ e ℏ i 2 π L z = 1 ⟹ ℏ 2 π L z = 2 mπ ⟹ L z = m ℏ
式中 m m m L ^ z \hat{L}_z L ^ z
L z = m ℏ ( m = 0 , ± 1 , ± 2 , ⋯ ) L_z = m\hbar \kern 2em (m=0,\pm1,\pm2,\cdots) L z = m ℏ ( m = 0 , ± 1 , ± 2 , ⋯ )
相应的本征函数表示为
ψ m ( φ ) = C e i m φ \psi_m(\varphi) = C \mathrm{e}^{\mathrm{i}m\varphi} ψ m ( φ ) = C e i m φ
按照归一化条件
( ψ m , ψ m ) = ∫ 0 2 π ∣ ψ m ( φ ) ∣ 2 d φ = 2 π ∣ C ∣ 2 = 1 (\psi_m,\psi_m) = \int_{0}^{2\pi} |\psi_m(\varphi)|^2\ \mathrm{d}\varphi = 2\pi|C|^2 = 1 ( ψ m , ψ m ) = ∫ 0 2 π ∣ ψ m ( φ ) ∣ 2 d φ = 2 π ∣ C ∣ 2 = 1
故可取 C = 1 2 π C=\frac{1}{\sqrt{2\pi}} C = 2 π 1
ψ m ( φ ) = 1 2 π e i m φ ( m = 0 , ± 1 , ± 2 , ⋯ ) \psi_m(\varphi) = \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\mathrm{i}m\varphi} \kern 2em (m=0,\pm1,\pm2,\cdots) ψ m ( φ ) = 2 π 1 e i m φ ( m = 0 , ± 1 , ± 2 , ⋯ )
容易证明这个本征函数系满足正交归一条件
( ψ m , ψ n ) = δ m n (\psi_m,\psi_n) = \delta_{mn} ( ψ m , ψ n ) = δ mn
球坐标下角动量平方算符
L ^ 2 = − ℏ 2 [ 1 sin θ ∂ ∂ θ ( sin θ ∂ ∂ θ ) + 1 sin 2 θ ∂ 2 ∂ φ 2 ] = − ℏ 2 1 sin θ ∂ ∂ θ ( sin θ ∂ ∂ θ ) + 1 sin 2 θ L ^ z 2 \hat{L}^2 = -\hbar^2 \left[ \frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\varphi^2} \right] \ \ \ = -\hbar^2 \frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right) + \frac{1}{\sin^2\theta} \hat{L}_z^2 L ^ 2 = − ℏ 2 [ sin θ 1 ∂ θ ∂ ( sin θ ∂ θ ∂ ) + sin 2 θ 1 ∂ φ 2 ∂ 2 ] = − ℏ 2 sin θ 1 ∂ θ ∂ ( sin θ ∂ θ ∂ ) + sin 2 θ 1 L ^ z 2
本征方程为
L ^ 2 Y ( θ , φ ) = λ ℏ 2 Y ( θ , φ ) \hat{L}^2 Y(\theta,\varphi) = \lambda \hbar^2Y(\theta,\varphi) L ^ 2 Y ( θ , φ ) = λ ℏ 2 Y ( θ , φ )
这里使用 λ ℏ 2 \lambda\hbar^2 λ ℏ 2 λ \lambda λ
考虑到 Y ( θ , φ ) Y(\theta,\varphi) Y ( θ , φ ) L ^ 2 \hat{L}^2 L ^ 2 L ^ z \hat{L}_z L ^ z 共同本征函数 ,则其与 φ \varphi φ ψ m ( φ ) \psi_m(\varphi) ψ m ( φ ) ψ m ( φ ) \psi_m(\varphi) ψ m ( φ ) θ \theta θ
Y ( θ , φ ) = Θ ( θ ) ψ m ( φ ) Y(\theta,\varphi) = \Theta(\theta) \psi_m(\varphi) Y ( θ , φ ) = Θ ( θ ) ψ m ( φ )
可以验证 Y ( θ , φ ) Y(\theta,\varphi) Y ( θ , φ ) L ^ z \hat{L}_z L ^ z
L ^ z Y ( θ , φ ) = L ^ z [ Θ ( θ ) ψ m ( φ ) ] = Θ ( θ ) [ L ^ z ψ m ( φ ) ] = Θ ( θ ) [ L z ψ m ( φ ) ] = L z Θ ( θ ) ψ m ( φ ) = L z Y ( θ , φ ) \hat{L}_z Y(\theta,\varphi) = \hat{L}_z \left[ \Theta(\theta) \psi_m(\varphi) \right] = \Theta(\theta) \left[ \hat{L}_z \psi_m(\varphi) \right] = \Theta(\theta) \left[ L_z \psi_m(\varphi) \right] = L_z \Theta(\theta) \psi_m(\varphi) = L_z Y(\theta,\varphi) L ^ z Y ( θ , φ ) = L ^ z [ Θ ( θ ) ψ m ( φ ) ] = Θ ( θ ) [ L ^ z ψ m ( φ ) ] = Θ ( θ ) [ L z ψ m ( φ ) ] = L z Θ ( θ ) ψ m ( φ ) = L z Y ( θ , φ )
将 Y ( θ , φ ) Y(\theta,\varphi) Y ( θ , φ ) L ^ 2 \hat{L}^2 L ^ 2
1 sin θ d d θ ( sin θ d d θ Θ ) + ( λ − m 2 sin 2 θ ) Θ = 0 \frac{1}{\sin\theta} \frac{\mathrm{d}}{\mathrm{d}\theta} \left( \sin\theta \frac{\mathrm{d}}{\mathrm{d}\theta} \Theta \right) + \left( \lambda - \frac{m^2}{\sin^2\theta} \right) \Theta = 0 sin θ 1 d θ d ( sin θ d θ d Θ ) + ( λ − sin 2 θ m 2 ) Θ = 0
其中 0 ≤ θ ≤ π 0 \le \theta \le \pi 0 ≤ θ ≤ π ξ = cos θ ( ∣ ξ ∣ ≤ 1 ) \xi = \cos\theta\ (|\xi|\le1) ξ = cos θ ( ∣ ξ ∣ ≤ 1 )
d d ξ [ ( 1 − ξ 2 ) d d ξ Θ ] + ( λ − m 2 1 − ξ 2 ) Θ = 0 \frac{\mathrm{d}}{\mathrm{d}\xi} \left[ (1-\xi^2) \frac{\mathrm{d}}{\mathrm{d}\xi} \Theta \right] + \left( \lambda - \frac{m^2}{1-\xi^2} \right) \Theta = 0 d ξ d [ ( 1 − ξ 2 ) d ξ d Θ ] + ( λ − 1 − ξ 2 m 2 ) Θ = 0
整理得
( 1 − ξ 2 ) d 2 d ξ 2 Θ − 2 ξ d d ξ Θ + ( λ − m 2 1 − ξ 2 ) Θ = 0 (1-\xi^2) \frac{\mathrm{d}^2}{\mathrm{d}\xi^2} \Theta - 2\xi \frac{\mathrm{d}}{\mathrm{d}\xi} \Theta + \left( \lambda - \frac{m^2}{1-\xi^2} \right) \Theta = 0 ( 1 − ξ 2 ) d ξ 2 d 2 Θ − 2 ξ d ξ d Θ + ( λ − 1 − ξ 2 m 2 ) Θ = 0
此方程为连带Legendre方程,其求解过程如下:
以下求解过程较为复杂,可以选择性阅读。
先考虑Legendre方程,即 m = 0 m=0 m = 0
( 1 − x 2 ) d 2 d x 2 y − 2 x d d x y + λ y = 0 (1-x^2) \frac{\mathrm{d}^2}{\mathrm{d}x^2} y - 2x \frac{\mathrm{d}}{\mathrm{d}x} y + \lambda y = 0 ( 1 − x 2 ) d x 2 d 2 y − 2 x d x d y + λ y = 0
此方程可以通过级数解法求解:在 x = 0 x=0 x = 0
y ( x ) = ∑ k = 0 + ∞ c k x k y(x) = \sum_{k=0}^{+\infty} c_k x^k y ( x ) = k = 0 ∑ + ∞ c k x k
代入Legendre方程,比较同幂项的系数,可得
c k + 2 = k ( k + 1 ) − λ ( k + 2 ) ( k + 1 ) c k ( k = 0 , 1 , 2 , ⋯ ) c_{k+2} = \frac{k(k+1)-\lambda}{(k+2)(k+1)} c_k \kern 2em (k=0,1,2,\cdots) c k + 2 = ( k + 2 ) ( k + 1 ) k ( k + 1 ) − λ c k ( k = 0 , 1 , 2 , ⋯ )
故所有的偶次项系数都可以用 c 0 c_0 c 0 c 1 c_1 c 1 c 0 c_0 c 0 c 1 c_1 c 1
y 1 ( x ) = ∑ n = 0 + ∞ c 2 n x 2 n = c 0 + c 2 x 2 + c 4 x 4 + ⋯ y 2 ( x ) = ∑ n = 0 + ∞ c 2 n + 1 x 2 n + 1 = c 1 x + c 3 x 3 + c 5 x 5 + ⋯ y_1(x) = \sum_{n=0}^{+\infty} c_{2n} x^{2n} = c_0 + c_2x^2 + c_4x^4 + \cdots \ \kern 1em \ y_2(x) = \sum_{n=0}^{+\infty} c_{2n+1} x^{2n+1} = c_1x + c_3x^3 + c_5x^5 + \cdots y 1 ( x ) = n = 0 ∑ + ∞ c 2 n x 2 n = c 0 + c 2 x 2 + c 4 x 4 + ⋯ y 2 ( x ) = n = 0 ∑ + ∞ c 2 n + 1 x 2 n + 1 = c 1 x + c 3 x 3 + c 5 x 5 + ⋯
考虑当 x → ± 1 x\to\pm1 x → ± 1 k → + ∞ k\to+\infty k → + ∞
c k + 2 c k = k ( k + 1 ) − λ ( k + 2 ) ( k + 1 ) → k k + 2 = 1 − 2 k + 2 \frac{c_{k+2}}{c_k} = \frac{k(k+1)-\lambda}{(k+2)(k+1)} \to \frac{k}{k+2} = 1-\frac{2}{k+2} c k c k + 2 = ( k + 2 ) ( k + 1 ) k ( k + 1 ) − λ → k + 2 k = 1 − k + 2 2
对于偶数的情况,即 k = 2 n k=2n k = 2 n c 2 n + 2 / c 2 n ∼ 1 − 1 / ( n + 1 ) c_{2n+2}/c_{2n} \sim 1-1/(n+1) c 2 n + 2 / c 2 n ∼ 1 − 1/ ( n + 1 ) ln ( 1 − x 2 ) \ln(1-x^2) ln ( 1 − x 2 )
ln ( 1 − x 2 ) = ∑ n = 0 + ∞ x 2 n n \ln(1-x^2) = \sum_{n=0}^{+\infty} \frac{x^{2n}}{n} ln ( 1 − x 2 ) = n = 0 ∑ + ∞ n x 2 n
相邻两项的系数比相同,因此,
y 1 ( x ) ∼ ln ( 1 − x 2 ) y_1(x) \sim \ln(1-x^2) y 1 ( x ) ∼ ln ( 1 − x 2 )
同理可得
y 2 ( x ) ∼ x ln ( 1 − x 2 ) y_2(x) \sim x\ln(1-x^2) y 2 ( x ) ∼ x ln ( 1 − x 2 )
然而,当 x → ± 1 x\to\pm1 x → ± 1
y 1 ( x ) → ∞ , y 2 ( x ) → ∞ y_1(x) \to \infty , \kern 1em y_2(x) \to \infty y 1 ( x ) → ∞ , y 2 ( x ) → ∞
这不是物理上可以接受的解,故 y 1 y_1 y 1 y 2 y_2 y 2 中断为多项式 ,也就是要找到合适的 λ \lambda λ k ∈ N k\in\mathbb{N} k ∈ N k ( k + 1 ) − λ ( k + 2 ) ( k + 1 ) = 0 \frac{k(k+1)-\lambda}{(k+2)(k+1)} = 0 ( k + 2 ) ( k + 1 ) k ( k + 1 ) − λ = 0
λ = l ( l + 1 ) ( l = 0 , 1 , 2 , ⋯ ) \lambda = l(l+1) \kern 2em (l=0,1,2,\cdots) λ = l ( l + 1 ) ( l = 0 , 1 , 2 , ⋯ )
时,级数将中断一个多项式( c l + 2 = c l + 4 = c l + 6 = ⋯ = 0 c_{l+2} = c_{l+4} = c_{l+6} = \cdots = 0 c l + 2 = c l + 4 = c l + 6 = ⋯ = 0 l l l y 1 y_1 y 1 P l ( x ) \mathrm{P}_l(x) P l ( x ) y 2 y_2 y 2 n n n y 2 y_2 y 2 P l ( x ) \mathrm{P}_l(x) P l ( x ) y 1 y_1 y 1 Legendre多项式 表示为
P l ( x ) = 1 2 l ⋅ l ! d l d x l ( x 2 − 1 ) l = ∑ k = 0 ⌊ l 2 ⌋ ( − 1 ) k ( 2 l − 2 k ) ! 2 l ⋅ k ! ( l − k ) ! ( l − 2 k ) ! x l − 2 k \mathrm{P}l(x) = \frac{1}{2^l\cdot l!} \frac{\mathrm{d}^l}{\mathrm{d}x^l} (x^2-1)^l \ \ \ = \sum {k=0}^{\left\lfloor \frac{l}{2} \right\rfloor} \frac{(-1)^k(2l-2k)!}{2^l\cdot k!(l-k)!(l-2k)!} x^{l-2k} P l ( x ) = 2 l ⋅ l ! 1 d x l d l ( x 2 − 1 ) l = k = 0 ∑ ⌊ 2 l ⌋ 2 l ⋅ k ! ( l − k )! ( l − 2 k )! ( − 1 ) k ( 2 l − 2 k )! x l − 2 k
例如
P 0 ( x ) = 1 P 1 ( x ) = x P 2 ( x ) = 1 2 ( 3 x 2 − 1 ) \mathrm{P}_0(x) = 1 \ \mathrm{P}_1(x) = x \ \mathrm{P}_2(x) = \frac12 (3x^2 - 1) P 0 ( x ) = 1 P 1 ( x ) = x P 2 ( x ) = 2 1 ( 3 x 2 − 1 )
Legendre多项式的正交性公式表示为
∫ − 1 1 P l ( x ) P l ′ ( x ) d x = 2 2 l + 1 δ l l ′ \int_{-1}^{1} \mathrm{P}l(x) \mathrm{P} {l'}(x) \mathrm{d}x = \frac{2}{2l+1} \delta_{ll'} ∫ − 1 1 P l ( x ) P l ′ ( x ) d x = 2 l + 1 2 δ l l ′
回到连带Legendre方程,先考虑在正则奇点 x = 1 x=1 x = 1 z = 1 − x z=1-x z = 1 − x
z ( 2 − z ) d 2 d z 2 y + 2 ( 1 − z ) d d z y + [ λ − m 2 z ( 2 − z ) ] y = 0 ⇓ d 2 d z 2 y + 2 ( 1 − z ) z ( 2 − z ) d d z y + [ λ z ( 2 − z ) − m 2 z 2 ( 2 − z ) 2 ] y = 0 z(2-z) \frac{\mathrm{d}^2}{\mathrm{d}z^2} y + 2(1-z) \frac{\mathrm{d}}{\mathrm{d}z} y + \left[ \lambda - \frac{m^2}{z(2-z)} \right] y = 0 \ \Downarrow \ \frac{\mathrm{d}^2}{\mathrm{d}z^2} y + \frac{2(1-z)}{z(2-z)} \frac{\mathrm{d}}{\mathrm{d}z} y + \left[ \frac{\lambda}{z(2-z)} - \frac{m^2}{z^2(2-z)^2} \right] y = 0 z ( 2 − z ) d z 2 d 2 y + 2 ( 1 − z ) d z d y + [ λ − z ( 2 − z ) m 2 ] y = 0 ⇓ d z 2 d 2 y + z ( 2 − z ) 2 ( 1 − z ) d z d y + [ z ( 2 − z ) λ − z 2 ( 2 − z ) 2 m 2 ] y = 0
在 z = 0 ( x = 1 ) z=0(x=1) z = 0 ( x = 1 ) 2 ( 1 − z ) 2 − z ∼ 1 \frac{2(1-z)}{2-z} \sim 1 2 − z 2 ( 1 − z ) ∼ 1 λ z ( 2 − z ) ∼ λ 2 z \frac{\lambda}{z(2-z)} \sim \frac{\lambda}{2z} z ( 2 − z ) λ ∼ 2 z λ m 2 z 2 ( 2 − z ) 2 ∼ m 2 4 z 2 \frac{m^2}{z^2(2-z)^2} \sim \frac{m^2}{4z^2} z 2 ( 2 − z ) 2 m 2 ∼ 4 z 2 m 2
d 2 d z 2 y + 1 z d d z y − m 2 4 z 2 y = 0 ⇓ z 2 d 2 y d z 2 + z d y d z − m 2 4 y = 0 \frac{\mathrm{d}^2}{\mathrm{d}z^2} y + \frac{1}{z} \frac{\mathrm{d}}{\mathrm{d}z} y - \frac{m^2}{4z^2} y = 0 \ \Downarrow \ z^2\frac{\mathrm{d}^2y}{\mathrm{d}z^2} +z \frac{\mathrm{d}y}{\mathrm{d}z} - \frac{m^2}{4} y = 0 d z 2 d 2 y + z 1 d z d y − 4 z 2 m 2 y = 0 ⇓ z 2 d z 2 d 2 y + z d z d y − 4 m 2 y = 0
此方程为欧拉方程,解具有 z s z^s z s
s ( s − 1 ) + s − m 2 4 = 0 s(s-1) + s - \frac{m^2}{4} = 0 s ( s − 1 ) + s − 4 m 2 = 0
解得 s = ± ∣ m ∣ 2 s=\pm\frac{|m|}{2} s = ± 2 ∣ m ∣ z = 0 z=0 z = 0 y ∝ z − ∣ m ∣ / 2 → ∞ y \propto z^{-|m|/2} \to \infty y ∝ z − ∣ m ∣/2 → ∞ z = 0 ( x = 1 ) z=0(x=1) z = 0 ( x = 1 )
y ∝ z ∣ m ∣ 2 = ( 1 − x ) ∣ m ∣ 2 y \propto z^{\frac{|m|}{2}} = (1-x)^{\frac{|m|}{2}} y ∝ z 2 ∣ m ∣ = ( 1 − x ) 2 ∣ m ∣
同理,在 x = − 1 x=-1 x = − 1
y ∝ ( 1 + x ) ∣ m ∣ 2 y \propto (1+x)^{\frac{|m|}{2}} y ∝ ( 1 + x ) 2 ∣ m ∣
故可令连带Legendre方程的解为
y ( x ) = ( 1 − x ) ∣ m ∣ 2 ( 1 + x ) ∣ m ∣ 2 v ( x ) = ( 1 − x 2 ) ∣ m ∣ 2 v ( x ) y(x) = (1-x)^{\frac{|m|}{2}}(1+x)^{\frac{|m|}{2}}v(x) = (1-x^2)^{\frac{|m|}{2}}v(x) y ( x ) = ( 1 − x ) 2 ∣ m ∣ ( 1 + x ) 2 ∣ m ∣ v ( x ) = ( 1 − x 2 ) 2 ∣ m ∣ v ( x )
代入连带Legendre方程
( 1 − x 2 ) d 2 y d x 2 − 2 x d y d x + ( λ − m 2 1 − x 2 ) y = 0 (1-x^2) \frac{\mathrm{d}^2y}{\mathrm{d}x^2} - 2x \frac{\mathrm{d}y}{\mathrm{d}x} + \left( \lambda - \frac{m^2}{1-x^2} \right) y = 0 ( 1 − x 2 ) d x 2 d 2 y − 2 x d x d y + ( λ − 1 − x 2 m 2 ) y = 0
可得
( 1 − x 2 ) v ′ ′ − 2 ( ∣ m ∣ + 1 ) x v ′ + [ λ − ∣ m ∣ ( ∣ m ∣ + 1 ) ] v = 0 (1-x^2)v'' - 2(|m|+1)xv' + [\lambda-|m|(|m|+1)]v = 0 ( 1 − x 2 ) v ′′ − 2 ( ∣ m ∣ + 1 ) x v ′ + [ λ − ∣ m ∣ ( ∣ m ∣ + 1 )] v = 0
该方程对 x x x
( 1 − x 2 ) v ′ ′ ′ − 2 ( ∣ m ∣ + 2 ) x v ′ ′ + [ λ − ( ∣ m ∣ + 1 ) ( ∣ m ∣ + 2 ) ] v ′ = 0 (1-x^2)v''' - 2(|m|+2)xv'' + [\lambda-(|m|+1)(|m|+2)]v' = 0 ( 1 − x 2 ) v ′′′ − 2 ( ∣ m ∣ + 2 ) x v ′′ + [ λ − ( ∣ m ∣ + 1 ) ( ∣ m ∣ + 2 )] v ′ = 0
可推得每经过一次求导,发生如下变换: ∣ m ∣ → ∣ m ∣ + 1 , v → v ′ |m|\to|m|+1,\ v\to v' ∣ m ∣ → ∣ m ∣ + 1 , v → v ′ m = 0 m=0 m = 0 ( 1 − x 2 ) v ′ ′ − 2 ( ∣ m ∣ + 1 ) x v ′ + [ λ − ∣ m ∣ ( ∣ m ∣ + 1 ) ] v = 0 (1-x^2)v'' - 2(|m|+1)xv' + [\lambda-|m|(|m|+1)]v = 0 ( 1 − x 2 ) v ′′ − 2 ( ∣ m ∣ + 1 ) x v ′ + [ λ − ∣ m ∣ ( ∣ m ∣ + 1 )] v = 0 ∣ m ∣ |m| ∣ m ∣ 0 0 0 ∣ m ∣ |m| ∣ m ∣ v v v ∣ m ∣ |m| ∣ m ∣ P l ( x ) \mathrm{P}_l(x) P l ( x )
v ( x ) = d ∣ m ∣ d x ∣ m ∣ P l ( x ) v(x) = \frac{\mathrm{d}^{|m|}}{\mathrm{d}x^{|m|}} \mathrm{P}_l(x) v ( x ) = d x ∣ m ∣ d ∣ m ∣ P l ( x )
这样就得到了连带Legendre方程物理上允许的解为连带Legendre多项式
P l ∣ m ∣ ( x ) = ( 1 − x 2 ) ∣ m ∣ 2 d ∣ m ∣ d x ∣ m ∣ P l ( x ) \mathrm{P}_{l}^{|m|} (x) = (1-x^2)^{\frac{|m|}{2}} \frac{\mathrm{d}^{|m|}}{\mathrm{d}x^{|m|}} \mathrm{P}_l(x) P l ∣ m ∣ ( x ) = ( 1 − x 2 ) 2 ∣ m ∣ d x ∣ m ∣ d ∣ m ∣ P l ( x )
对于 m ≥ 0 m\ge0 m ≥ 0
P l m ( x ) = ( 1 − x 2 ) m 2 d m d x m P l ( x ) \mathrm{P}_{l}^{m} (x) = (1-x^2)^{\frac{m}{2}} \frac{\mathrm{d}^{m}}{\mathrm{d}x^{m}} \mathrm{P}_l(x) P l m ( x ) = ( 1 − x 2 ) 2 m d x m d m P l ( x )
将 P l ( x ) \mathrm{P}_l(x) P l ( x )
P l m ( x ) = 1 2 l ⋅ l ! ( 1 − x 2 ) m 2 d l + m d x l + m ( x 2 − 1 ) l \mathrm{P}_{l}^{m} (x) = \frac{1}{2^l\cdot l!} (1-x^2)^{\frac{m}{2}} \frac{\mathrm{d}^{l+m}}{\mathrm{d}x^{l+m}} (x^2-1)^l P l m ( x ) = 2 l ⋅ l ! 1 ( 1 − x 2 ) 2 m d x l + m d l + m ( x 2 − 1 ) l
该式对于 − l ≤ m < 0 -l \le m < 0 − l ≤ m < 0
P l − m ( x ) = ( − 1 ) m ( l − m ) ! ( l + m ) ! P l m ( x ) \mathrm{P}{l}^{-m} (x) = (-1)^m \frac{(l-m)!}{(l+m)!} \mathrm{P} {l}^{m} (x) P l − m ( x ) = ( − 1 ) m ( l + m )! ( l − m )! P l m ( x )
连带Legendre多项式的正交性公式表示为
∫ − 1 1 P l m ( x ) P l ′ m ( x ) d x = ( l + m ) ! ( l − m ) ! 2 2 l + 1 δ l l ′ \int_{-1}^{1} \mathrm{P}l^m(x) \mathrm{P}^m {l'}(x) \mathrm{d}x = \frac{(l+m)!}{(l-m)!} \frac{2}{2l+1} \delta_{ll'} ∫ − 1 1 P l m ( x ) P l ′ m ( x ) d x = ( l − m )! ( l + m )! 2 l + 1 2 δ l l ′
这样就基本完成了算符 L ^ 2 \hat{L}^2 L ^ 2 球谐函数
Y l m ( θ , φ ) = N l m P l m ( cos θ ) ψ m ( φ ) \mathrm{Y}{lm} (\theta,\varphi) = N {lm} \mathrm{P}^m_l(\cos\theta) \psi_m(\varphi) Y l m ( θ , φ ) = N l m P l m ( cos θ ) ψ m ( φ )
其中归一化系数
N l m = ( − 1 ) m 2 l + 1 4 π ( l − m ) ! ( l + m ) ! N_{lm} = (-1)^m \sqrt{\frac{2l+1}{4\pi} \frac{(l-m)!}{(l+m)!}} N l m = ( − 1 ) m 4 π 2 l + 1 ( l + m )! ( l − m )!
故
Y l m ( θ , φ ) = ( − 1 ) m 2 l + 1 4 π ( l − m ) ! ( l + m ) ! P l m ( cos θ ) e i m φ \mathrm{Y}_{lm} (\theta,\varphi) = (-1)^m \sqrt{\frac{2l+1}{4\pi} \frac{(l-m)!}{(l+m)!}}\ \mathrm{P}_l^m (\cos\theta)\ \mathrm{e}^{\mathrm{i}m\varphi} Y l m ( θ , φ ) = ( − 1 ) m 4 π 2 l + 1 ( l + m )! ( l − m )! P l m ( cos θ ) e i m φ
其满足
L ^ 2 Y l m = l ( l + 1 ) ℏ 2 Y l m L ^ z Y l m = m ℏ Y l m \hat{L}^2 \mathrm{Y}{lm} = l(l+1) \hbar^2 \mathrm{Y} {lm} \ \hat{L}z \mathrm{Y} {lm} = m\hbar \mathrm{Y}_{lm} L ^ 2 Y l m = l ( l + 1 ) ℏ 2 Y l m L ^ z Y l m = m ℏ Y l m
其中 l = 0 , 1 , 2 , ⋯ , m = l , l − 1 , ⋯ , − l + 1 , − l l=0,1,2,\cdots, \kern 1em m=l,l-1,\cdots,-l+1,-l l = 0 , 1 , 2 , ⋯ , m = l , l − 1 , ⋯ , − l + 1 , − l
∫ 0 2 π d φ ∫ 0 π sin θ d θ Y l m ∗ ( θ , φ ) Y l ′ m ′ ( θ , φ ) = δ l l ′ δ m m ′ \int_{0}^{2\pi} \mathrm{d}\varphi \int_{0}^{\pi} \sin\theta \mathrm{d}\theta \mathrm{Y}{lm}^*(\theta,\varphi) Y {l'm'}(\theta,\varphi) = \delta_{ll'} \delta_{mm'} ∫ 0 2 π d φ ∫ 0 π sin θ d θ Y l m ∗ ( θ , φ ) Y l ′ m ′ ( θ , φ ) = δ l l ′ δ m m ′
头两阶球谐函数为
Y 0 , 0 ( θ , φ ) = 1 4 π Y 1 , 0 ( θ , φ ) = 3 4 π cos θ Y 1 , ± 1 ( θ , φ ) = ∓ 3 8 π sin θ e ± i φ \mathrm{Y}{0,0}(\theta,\varphi) = \frac{1}{\sqrt{4\pi}} \ \ \ \mathrm{Y} {1,0}(\theta,\varphi) = \sqrt{\frac{3}{4\pi}} \cos\theta \ \ \ \mathrm{Y}_{1,\pm1}(\theta,\varphi) = \mp\sqrt{\frac{3}{8\pi}} \sin\theta \mathrm{e}^{\pm\mathrm{i}\varphi} Y 0 , 0 ( θ , φ ) = 4 π 1 Y 1 , 0 ( θ , φ ) = 4 π 3 cos θ Y 1 , ± 1 ( θ , φ ) = ∓ 8 π 3 sin θ e ± i φ
定义算符 A ^ \hat{A} A ^
Δ A ^ = A ^ − A ˉ \Delta\hat{A} = \hat{A} - \bar{A} Δ A ^ = A ^ − A ˉ
容易发现 Δ A ^ \Delta\hat{A} Δ A ^ Δ A ^ ‾ = A ^ − A ˉ ‾ = A ˉ − A ˉ = 0 \overline{\Delta\hat{A}} = \overline{\hat{A} - \bar{A}} = \bar{A} - \bar{A} = 0 Δ A ^ = A ^ − A ˉ = A ˉ − A ˉ = 0
每次测量的结果围绕平均值有一个涨落 ,其定义为
( Δ A ^ ) 2 ‾ = ( A ^ − A ˉ ) 2 ‾ = A ^ 2 − 2 A ^ A ˉ + A ˉ 2 ‾ = A ^ 2 ‾ − 2 A ˉ A ˉ + A ˉ 2 = A ^ 2 ‾ − A ˉ 2 \overline{(\Delta\hat{A})^2} = \overline{(\hat{A} - \bar{A})^2} = \overline{\hat{A}^2 - 2\hat{A}\bar{A} + \bar{A}^2} = \overline{\hat{A}^2} - 2\bar{A}\bar{A} + \bar{A}^2 = \overline{\hat{A}^2} - \bar{A}^2 ( Δ A ^ ) 2 = ( A ^ − A ˉ ) 2 = A ^ 2 − 2 A ^ A ˉ + A ˉ 2 = A ^ 2 − 2 A ˉ A ˉ + A ˉ 2 = A ^ 2 − A ˉ 2
这个量描写了力学量 A A A
在态 ψ \psi ψ A A A 不确定度 为
Δ A = ( Δ A ^ ) 2 ‾ = A ^ 2 ‾ − A ˉ 2 \Delta A = \sqrt{\overline{(\Delta\hat{A})^2}} = \sqrt{\overline{\hat{A}^2} - \bar{A}^2} Δ A = ( Δ A ^ ) 2 = A ^ 2 − A ˉ 2
在任意量子态 ψ \psi ψ A , B A,B A , B
Δ A ⋅ Δ B ≥ 1 2 ∣ [ A ^ , B ^ ] ‾ ∣ = 1 2 ∣ ( ψ , [ A ^ , B ^ ] ψ ) ∣ \Delta A \cdot \Delta B \ge \frac12 \left| \overline{[\hat{A},\hat{B}]} \right| = \frac12 \left| (\psi, [\hat{A},\hat{B}]\psi) \right| Δ A ⋅ Δ B ≥ 2 1 [ A ^ , B ^ ] = 2 1 ( ψ , [ A ^ , B ^ ] ψ )
当 [ A ^ , B ^ ] ≠ 0 [\hat{A},\hat{B}] \ne 0 [ A ^ , B ^ ] = 0 [ A ^ , B ^ ] ‾ = ( ψ , [ A ^ , B ^ ] ψ ) = 0 \overline{[\hat{A},\hat{B}]} = (\psi,[\hat{A},\hat{B}]\psi) = 0 [ A ^ , B ^ ] = ( ψ , [ A ^ , B ^ ] ψ ) = 0 A , B A,B A , B [ A ^ , B ^ ] = 0 [\hat{A},\hat{B}] = 0 [ A ^ , B ^ ] = 0 A , B A,B A , B
这里的特殊情况,例如氢原子的基态 ψ 100 ( r , θ , φ ) \psi_{100}(r,\theta,\varphi) ψ 100 ( r , θ , φ ) L = 0 L=0 L = 0 z z z L z = 0 L_z=0 L z = 0 L x = L y = 0 L_x = L_y = 0 L x = L y = 0 L x , L y , L z L_x,L_y,L_z L x , L y , L z L x , L y , L z L_x,L_y,L_z L x , L y , L z [ L ^ x , L ^ y ] ‾ = i ℏ L ^ z ‾ = 0 \overline{[\hat{L}_x,\hat{L}_y]} = \overline{\mathrm{i}\hbar\hat{L}_z} = 0 [ L ^ x , L ^ y ] = i ℏ L ^ z = 0
说明:
不确定度关系是微观粒子运动的基本规律,在宏观世界不能得到直接的体现;
不确定度关系是微观粒子固有属性决定的,与仪器精度和测量方法的缺陷无关;
不确定度关系不是给物理学带来了不精确性,而正是体现了微观世界的精确性;
不确定度关系给出了微观世界中应用经典粒子的坐标和动量概念时应受到的限制,展示了量子力学与经典力学规律的本质区别。
波动性使微观粒子没有确定的轨道, 即坐标和动量不能同时取确定值, 它们存在一个不确定度关系
Δ x Δ p x ≥ ℏ 2 , Δ y Δ p y ≥ ℏ 2 , Δ z Δ p z ≥ ℏ 2 \Delta x \Delta p_x \ge \frac{\hbar}{2} ,\kern 1em \Delta y \Delta p_y \ge \frac{\hbar}{2} ,\kern 1em \Delta z \Delta p_z \ge \frac{\hbar}{2} Δ x Δ p x ≥ 2 ℏ , Δ y Δ p y ≥ 2 ℏ , Δ z Δ p z ≥ 2 ℏ
Δ E Δ t ≥ ℏ 2 \Delta E \Delta t \ge \frac{\hbar}{2} Δ E Δ t ≥ 2 ℏ
时间实际上不是力学量,这个不确定度关系不能直接用上述方法得到。
能量与时间的不确定关系式说明了原子的激发态能级都有一定的能级宽度 , 实验原子发光都有一定的频率宽度 。
Δ L z Δ φ ≥ ℏ 2 \Delta L_z \Delta \varphi \ge \frac{\hbar}{2} Δ L z Δ φ ≥ 2 ℏ
由 A ^ , B ^ \hat{A},\hat{B} A ^ , B ^ A ˉ , B ˉ \bar{A},\bar{B} A ˉ , B ˉ Δ A ^ = A ^ − A ˉ , Δ B ^ = B ^ − B ˉ \Delta\hat{A}=\hat{A}-\bar{A},\ \Delta\hat{B}=\hat{B}-\bar{B} Δ A ^ = A ^ − A ˉ , Δ B ^ = B ^ − B ˉ
I ( ξ ) = ∫ ∣ ( ξ Δ A ^ + i B ^ ) ψ ∣ 2 d τ ≥ 0 I(\xi) = \int \left| (\xi\Delta\hat{A} + \mathrm{i}\hat{B}) \psi \right|^2 \mathrm{d}\tau \ge 0 I ( ξ ) = ∫ ( ξ Δ A ^ + i B ^ ) ψ 2 d τ ≥ 0
其中 ξ \xi ξ
I ( ξ ) = ∫ ( ξ Δ A ^ ψ + i B ^ ψ ) ∗ ( ξ Δ A ^ ψ + i B ^ ψ ) d τ = ∫ [ ξ ( Δ A ^ ψ ) ∗ − i ( B ^ ψ ) ∗ ] [ ξ ( Δ A ^ ψ ) + i ( B ^ ψ ) ] d τ = ξ 2 ∫ ( Δ A ^ ψ ) ∗ ( Δ A ^ ψ ) d τ + i ξ ∫ ( Δ A ^ ψ ) ∗ ( Δ B ^ ψ ) d τ − i ξ ∫ ( Δ B ^ ψ ) ∗ ( Δ A ^ ψ ) d τ + ∫ ( Δ B ^ ψ ) ∗ ( Δ B ^ ψ ) d τ = ξ 2 ( Δ A ^ ψ , Δ A ^ ψ ) + i ξ ( Δ A ^ ψ , Δ B ^ ψ ) − i ξ ( Δ B ^ ψ , Δ A ^ ψ ) + ( Δ B ^ ψ , Δ B ^ ψ ) = ξ 2 ( ψ , ( Δ A ^ ) 2 ψ ) + i ξ ( ψ , Δ A ^ Δ B ^ ψ ) − i ξ ( ψ , Δ B ^ Δ A ^ ψ ) + ( ψ , ( Δ B ^ ) 2 ψ ) = ξ 2 ( Δ A ^ ) 2 ‾ + i ξ ( Δ A ^ Δ B ^ − Δ B ^ Δ A ^ ‾ ) + ( Δ B ^ ) 2 ‾ = ξ 2 ( Δ A ^ ) 2 ‾ + i ξ [ Δ A ^ , Δ B ^ ] ‾ + ( Δ B ^ ) 2 ‾ I(\xi) = \int \left( \xi\Delta\hat{A}\psi + \mathrm{i}\hat{B}\psi \right)^* \left( \xi\Delta\hat{A}\psi+\mathrm{i}\hat{B}\psi \right) \mathrm{d}\tau \ \ \ = \int \left[ \xi\left(\Delta\hat{A}\psi\right)^* - \mathrm{i}\left(\hat{B}\psi\right)^* \right] \left[ \xi\left(\Delta\hat{A}\psi\right) + \mathrm{i}\left(\hat{B}\psi\right) \right] \mathrm{d}\tau \ \ \ = \xi^2 \int \left(\Delta\hat{A}\psi\right)^* \left(\Delta\hat{A}\psi\right) \mathrm{d}\tau + \mathrm{i}\xi \int \left(\Delta\hat{A}\psi\right)^* \left(\Delta\hat{B}\psi\right) \mathrm{d}\tau - \mathrm{i}\xi \int \left(\Delta\hat{B}\psi\right)^* \left(\Delta\hat{A}\psi\right) \mathrm{d}\tau + \int \left(\Delta\hat{B}\psi\right)^* \left(\Delta\hat{B}\psi\right) \mathrm{d}\tau \ \ \ = \xi^2 \left(\Delta\hat{A}\psi , \Delta\hat{A}\psi\right) + \mathrm{i}\xi \left(\Delta\hat{A}\psi , \Delta\hat{B}\psi\right) - \mathrm{i}\xi \left(\Delta\hat{B}\psi , \Delta\hat{A}\psi\right) + \left(\Delta\hat{B}\psi , \Delta\hat{B}\psi\right) \ \ \ = \xi^2 \left(\psi , (\Delta\hat{A})^2\psi\right) + \mathrm{i}\xi \left(\psi , \Delta\hat{A}\Delta\hat{B}\psi\right) - \mathrm{i}\xi \left(\psi , \Delta\hat{B}\Delta\hat{A}\psi\right) + \left(\psi , (\Delta\hat{B})^2\psi\right) \ \ \ = \xi^2 \overline{(\Delta\hat{A})^2} + \mathrm{i}\xi \left( \overline{\Delta\hat{A}\Delta\hat{B}-\Delta\hat{B}\Delta\hat{A}}\right) + \overline{(\Delta\hat{B})^2} \ \ \ = \xi^2 \overline{(\Delta\hat{A})^2} + \mathrm{i}\xi \overline{[\Delta\hat{A} , \Delta\hat{B}]} + \overline{(\Delta\hat{B})^2} I ( ξ ) = ∫ ( ξ Δ A ^ ψ + i B ^ ψ ) ∗ ( ξ Δ A ^ ψ + i B ^ ψ ) d τ = ∫ [ ξ ( Δ A ^ ψ ) ∗ − i ( B ^ ψ ) ∗ ] [ ξ ( Δ A ^ ψ ) + i ( B ^ ψ ) ] d τ = ξ 2 ∫ ( Δ A ^ ψ ) ∗ ( Δ A ^ ψ ) d τ + i ξ ∫ ( Δ A ^ ψ ) ∗ ( Δ B ^ ψ ) d τ − i ξ ∫ ( Δ B ^ ψ ) ∗ ( Δ A ^ ψ ) d τ + ∫ ( Δ B ^ ψ ) ∗ ( Δ B ^ ψ ) d τ = ξ 2 ( Δ A ^ ψ , Δ A ^ ψ ) + i ξ ( Δ A ^ ψ , Δ B ^ ψ ) − i ξ ( Δ B ^ ψ , Δ A ^ ψ ) + ( Δ B ^ ψ , Δ B ^ ψ ) = ξ 2 ( ψ , ( Δ A ^ ) 2 ψ ) + i ξ ( ψ , Δ A ^ Δ B ^ ψ ) − i ξ ( ψ , Δ B ^ Δ A ^ ψ ) + ( ψ , ( Δ B ^ ) 2 ψ ) = ξ 2 ( Δ A ^ ) 2 + i ξ ( Δ A ^ Δ B ^ − Δ B ^ Δ A ^ ) + ( Δ B ^ ) 2 = ξ 2 ( Δ A ^ ) 2 + i ξ [ Δ A ^ , Δ B ^ ] + ( Δ B ^ ) 2
考虑 [ A ^ , B ^ ] [\hat{A},\hat{B}] [ A ^ , B ^ ] [ Δ A ^ , Δ B ^ ] [\Delta\hat{A},\Delta\hat{B}] [ Δ A ^ , Δ B ^ ]
[ Δ A ^ , Δ B ^ ] = [ A ^ − A ˉ , B ^ − B ˉ ] = [ A ^ , B ^ ] [\Delta\hat{A},\Delta\hat{B}] = [\hat{A}-\bar{A},\hat{B}-\bar{B}] = [\hat{A},\hat{B}] [ Δ A ^ , Δ B ^ ] = [ A ^ − A ˉ , B ^ − B ˉ ] = [ A ^ , B ^ ]
由于上述连等式中所有等号连接的均为实数,引入厄米算符 C ^ = [ A ^ , B ^ ] / i = C ^ + \hat{C} = [\hat{A},\hat{B}]\ /\ \mathrm{i} = \hat{C}^+ C ^ = [ A ^ , B ^ ] / i = C ^ +
I ( ξ ) = ξ 2 ( Δ A ^ ) 2 ‾ + i ξ [ A ^ , B ^ ] ‾ + ( Δ B ^ ) 2 ‾ = ( Δ A ^ ) 2 ‾ ξ 2 − C ^ ‾ ξ + ( Δ B ^ ) 2 ‾ = ( Δ A ^ ) 2 ‾ ( ξ − C ^ ‾ 2 ( Δ A ^ ) 2 ‾ ) 2 + ( ( Δ B ^ ) 2 ‾ − C ^ ‾ 2 4 ( Δ A ^ ) 2 ‾ ) ≥ 0 I(\xi) = \xi^2 \overline{(\Delta\hat{A})^2} + \mathrm{i}\xi \overline{[\hat{A} , \hat{B}]} + \overline{(\Delta\hat{B})^2} = \overline{(\Delta\hat{A})^2} \xi^2 - \overline{\hat{C}} \xi + \overline{(\Delta\hat{B})^2} \ \ \ = \overline{(\Delta\hat{A})^2} \left( \xi - \frac{\overline{\hat{C}}}{2\overline{(\Delta\hat{A})^2}} \right)^2 + \left( \overline{(\Delta\hat{B})^2} - \frac{\overline{\hat{C}}^2}{4\overline{(\Delta\hat{A})^2}} \right) \ge 0 I ( ξ ) = ξ 2 ( Δ A ^ ) 2 + i ξ [ A ^ , B ^ ] + ( Δ B ^ ) 2 = ( Δ A ^ ) 2 ξ 2 − C ^ ξ + ( Δ B ^ ) 2 = ( Δ A ^ ) 2 ( ξ − 2 ( Δ A ^ ) 2 C ^ ) 2 + ( Δ B ^ ) 2 − 4 ( Δ A ^ ) 2 C ^ 2 ≥ 0
由于 ξ \xi ξ I ( ξ ) I(\xi) I ( ξ )
( Δ B ^ ) 2 ‾ − C ^ ‾ 2 4 ( Δ A ^ ) 2 ‾ ≥ 0 ⟹ ( Δ A ^ ) 2 ‾ ⋅ ( Δ B ^ ) 2 ‾ − C ^ ‾ 2 4 ≥ 0 ⟹ Δ A Δ B ≥ ∣ C ^ ‾ ∣ 2 = 1 2 ∣ [ A ^ , B ^ ] ‾ ∣ \overline{(\Delta\hat{B})^2} -\frac{\overline{\hat{C}}^2}{4\overline{(\Delta\hat{A})^2}} \ge 0 \Longrightarrow \overline{(\Delta\hat{A})^2} \cdot \overline{(\Delta\hat{B})^2} -\frac{\overline{\hat{C}}^2}{4} \ge 0 \Longrightarrow \Delta A \Delta B \ge \frac{\left|\overline{\hat{C}}\right|}{2} = \frac12 \left| \overline{[\hat{A},\hat{B}]} \right| ( Δ B ^ ) 2 − 4 ( Δ A ^ ) 2 C ^ 2 ≥ 0 ⟹ ( Δ A ^ ) 2 ⋅ ( Δ B ^ ) 2 − 4 C ^ 2 ≥ 0 ⟹ Δ A Δ B ≥ 2 C ^ = 2 1 [ A ^ , B ^ ]
一维谐振子的Hamiton算符
H ^ = 1 2 m p ^ 2 + 1 2 m ω 2 x ^ 2 \hat{H} = \frac{1}{2m} \hat{p}^2 + \frac12 m\omega^2 \hat{x}^2 H ^ = 2 m 1 p ^ 2 + 2 1 m ω 2 x ^ 2
能量本征函数为
ψ n ( x ) = A n e − α 2 x 2 2 H n ( α x ) \psi_n(x) = A_n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) ψ n ( x ) = A n e − 2 α 2 x 2 H n ( αx )
其中 α = m ω ℏ \alpha = \sqrt{\frac{m\omega}{\hbar}} α = ℏ mω H n \mathrm{H}_n H n A n A_n A n x x x p p p
x ˉ = ( ψ , x ^ ψ ) = ∫ − ∞ + ∞ A n e − α 2 x 2 2 H n ( α x ) x A n e − α 2 x 2 2 H n ( α x ) d x = A n 2 ∫ − ∞ + ∞ e − α 2 x 2 H n 2 ( α x ) x d x = 0 \bar{x} = (\psi , \hat{x}\psi) = \int_{-\infty}^{+\infty} A_n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) \ x \ A_n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}n(\alpha x) \ \mathrm{d} x \ \ \ = A_n^2 \int {-\infty}^{+\infty} \mathrm{e}^{-\alpha^2x^2} \ \mathrm{H}_n^2(\alpha x) \ x \ \mathrm{d}x = 0 x ˉ = ( ψ , x ^ ψ ) = ∫ − ∞ + ∞ A n e − 2 α 2 x 2 H n ( αx ) x A n e − 2 α 2 x 2 H n ( αx ) d x = A n 2 ∫ − ∞ + ∞ e − α 2 x 2 H n 2 ( αx ) x d x = 0
最后一个等号是因为被积函数是奇函数( H n ( − x ) = ( − 1 ) n H n ( x ) \mathrm{H}_n(-x) = (-1)^n \mathrm{H}_n(x) H n ( − x ) = ( − 1 ) n H n ( x )
p ˉ = ( ψ , p ^ ψ ) = ∫ − ∞ + ∞ A n e − α 2 x 2 2 H n ( α x ) ℏ i d d x [ A n e − α 2 x 2 2 H n ( α x ) ] d x = − i ℏ A n 2 ∫ − ∞ + ∞ e − α 2 x 2 2 H n ( α x ) d d x [ e − α 2 x 2 2 H n ( α x ) ] d x = − i ℏ A n 2 e − α 2 x 2 H n 2 ( α x ) ∣ − ∞ + ∞ + i ℏ A n 2 ∫ − ∞ + ∞ e − α 2 x 2 2 H n ( α x ) d d x [ e − α 2 x 2 2 H n ( α x ) ] d x = i ℏ A n 2 ∫ − ∞ + ∞ e − α 2 x 2 2 H n ( α x ) d d x [ e − α 2 x 2 2 H n ( α x ) ] d x \bar{p} = (\psi , \hat{p}\psi) = \int_{-\infty}^{+\infty} A_n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) \ \frac{\hbar}{\mathrm{i}}\frac{\mathrm{d}}{\mathrm{d}x} \left[ A_n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}n(\alpha x) \right] \mathrm{d} x \ \ \ = -\mathrm{i}\hbar A_n^2 \int {-\infty}^{+\infty} \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) \ \frac{\mathrm{d}}{\mathrm{d}x} \left[ \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}n(\alpha x) \right] \mathrm{d} x \ \ \ = \left. -\mathrm{i}\hbar A_n^2 \mathrm{e}^{-\alpha^2x^2} \ \mathrm{H}n^2(\alpha x) \right| {-\infty}^{+\infty} +\ \mathrm{i}\hbar A_n^2 \int {-\infty}^{+\infty} \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) \ \frac{\mathrm{d}}{\mathrm{d}x} \left[ \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}n(\alpha x) \right] \mathrm{d} x \ \ \ = \mathrm{i}\hbar A_n^2 \int {-\infty}^{+\infty} \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) \ \frac{\mathrm{d}}{\mathrm{d}x} \left[ \mathrm{e}^{-\frac{\alpha^2x^2}{2}} \mathrm{H}_n(\alpha x) \right] \mathrm{d} x p ˉ = ( ψ , p ^ ψ ) = ∫ − ∞ + ∞ A n e − 2 α 2 x 2 H n ( αx ) i ℏ d x d [ A n e − 2 α 2 x 2 H n ( αx ) ] d x = − i ℏ A n 2 ∫ − ∞ + ∞ e − 2 α 2 x 2 H n ( αx ) d x d [ e − 2 α 2 x 2 H n ( αx ) ] d x = − i ℏ A n 2 e − α 2 x 2 H n 2 ( αx ) − ∞ + ∞ + i ℏ A n 2 ∫ − ∞ + ∞ e − 2 α 2 x 2 H n ( αx ) d x d [ e − 2 α 2 x 2 H n ( αx ) ] d x = i ℏ A n 2 ∫ − ∞ + ∞ e − 2 α 2 x 2 H n ( αx ) d x d [ e − 2 α 2 x 2 H n ( αx ) ] d x
第三行的通过分部积分法得到
由第二行与第四行相等可得 p ˉ = − p ˉ \bar{p} = -\bar{p} p ˉ = − p ˉ p ˉ = 0 \bar{p} = 0 p ˉ = 0
由 Δ A = A ^ 2 ‾ − A ˉ 2 \Delta A = \sqrt{\overline{\hat{A}^2} - \bar{A}^2} Δ A = A ^ 2 − A ˉ 2
( Δ x ) 2 = x ^ 2 ‾ , ( Δ p ) 2 = p ^ 2 ‾ (\Delta x)^2 = \overline{\hat{x}^2} ,\kern 1em (\Delta p)^2 = \overline{\hat{p}^2} ( Δ x ) 2 = x ^ 2 , ( Δ p ) 2 = p ^ 2
故
E ˉ = 1 2 m p ^ 2 ‾ + 1 2 m ω 2 x ^ 2 ‾ = 1 2 m ( Δ p ) 2 + 1 2 m ω 2 ( Δ x ) 2 ≥ 2 1 2 m ( Δ p ) 2 ⋅ 1 2 m ω 2 ( Δ x ) 2 = ω Δ p Δ x ≥ 1 2 ℏ ω \bar{E} = \frac{1}{2m} \overline{\hat{p}^2} + \frac12 m\omega^2 \overline{\hat{x}^2} \ \ \ = \frac{1}{2m} (\Delta p)^2 + \frac12 m\omega^2 (\Delta x)^2 \ \ \ \ge 2 \sqrt{ \frac{1}{2m} (\Delta p)^2 \cdot \frac12 m\omega^2 (\Delta x)^2 } \ \ \ = \omega \Delta p \Delta x \ \ \ \ge \frac12 \hbar\omega E ˉ = 2 m 1 p ^ 2 + 2 1 m ω 2 x ^ 2 = 2 m 1 ( Δ p ) 2 + 2 1 m ω 2 ( Δ x ) 2 ≥ 2 2 m 1 ( Δ p ) 2 ⋅ 2 1 m ω 2 ( Δ x ) 2 = ω Δ p Δ x ≥ 2 1 ℏ ω
即得一维谐振子的零点能为
E ˉ min = 1 2 ℏ ω \bar{E}_{\min} = \frac12 \hbar\omega E ˉ m i n = 2 1 ℏ ω
非零的零点能是不确定度关系的结果。
求证:在 L z L_z L z Y l m \mathrm{Y}_{lm} Y l m L x L_x L x L y L_y L y
( Δ L ^ x ) 2 ‾ ⋅ ( Δ L ^ y ) 2 ‾ ≥ m 2 ℏ 4 4 \overline{(\Delta\hat{L}_x)^2} \cdot \overline{(\Delta\hat{L}_y)^2} \ge \frac{m^2\hbar^4}{4} ( Δ L ^ x ) 2 ⋅ ( Δ L ^ y ) 2 ≥ 4 m 2 ℏ 4
L ^ z \hat{L}_z L ^ z
L ^ z Y l m = m ℏ Y l m \hat{L}z \mathrm{Y} {lm} = m\hbar \mathrm{Y}_{lm} L ^ z Y l m = m ℏ Y l m
根据对易关系 [ L ^ x , L ^ y ] = i ℏ L ^ z [\hat{L}_x,\hat{L}_y] = \mathrm{i}\hbar \hat{L}_z [ L ^ x , L ^ y ] = i ℏ L ^ z
Δ L x Δ L y ≥ 1 2 ∣ [ L ^ x , L ^ y ] ‾ ∣ = ℏ 2 ∣ L ^ z ‾ ∣ = m ℏ 2 2 \Delta L_x \Delta L_y \ge \frac12 \left| \overline{[\hat{L}_x,\hat{L}_y]} \right| = \frac{\hbar}{2} \left|\overline{\hat{L}_z}\right| = \frac{m\hbar^2}{2} Δ L x Δ L y ≥ 2 1 [ L ^ x , L ^ y ] = 2 ℏ L ^ z = 2 m ℏ 2
故
( Δ L ^ x ) 2 ‾ ⋅ ( Δ L ^ y ) 2 ‾ ≥ m 2 ℏ 4 4 \overline{(\Delta\hat{L}_x)^2} \cdot \overline{(\Delta\hat{L}_y)^2} \ge \frac{m^2\hbar^4}{4} ( Δ L ^ x ) 2 ⋅ ( Δ L ^ y ) 2 ≥ 4 m 2 ℏ 4
本节可以视作《线性代数入门》 第7章“线性空间和线性映射”在量子力学中的具体应用,在后续部分会具体给出参考小节。
本部分可参考《线性代数入门》 第7.4节“向量的坐标表示”。
任何一个可归一化的量子态 ψ \psi ψ 矢量 ,体系的任何一组对易力学量完全集 F F F { ψ k ( x ) } {\psi_k(x)} { ψ k ( x )} 基矢 (满足 ( ψ k , ψ j ) = δ k j (\psi_k,\psi_j)=\delta_{kj} ( ψ k , ψ j ) = δ kj F F F 表象 , F F F A ^ \hat{A} A ^
A ^ ψ k = A k ψ k \hat{A} \psi_{k} = A_k \psi_k A ^ ψ k = A k ψ k
体系的任何一个态 ψ \psi ψ { ψ k } {\psi_k} { ψ k }
ψ ( x , t ) = ∑ k a k ( t ) ψ k ( x ) \psi(x,t) = \sum_{k} a_k(t)\ \psi_k(x) ψ ( x , t ) = k ∑ a k ( t ) ψ k ( x )
其中 a k ( t ) = ( ψ k , ψ ) a_k(t) = (\psi_k,\psi) a k ( t ) = ( ψ k , ψ ) ( a 1 , a 2 , ⋯ ) (a_1,a_2,\cdots) ( a 1 , a 2 , ⋯ ) ψ \psi ψ F F F { a k ( t ) , k = 1 , 2 , ⋯ } {a_k(t),\ k=1,2,\cdots} { a k ( t ) , k = 1 , 2 , ⋯ } F F F F F F
Ψ ( t ) = [ a 1 ( t ) a 2 ( t ) ⋮ a n ( t ) ⋮ ] \Psi(t) = \begin{bmatrix} a_1(t) \ a_2(t) \ \vdots \ a_n(t) \ \vdots \end{bmatrix} Ψ ( t ) = a 1 ( t ) a 2 ( t ) ⋮ a n ( t ) ⋮
这样就用一个向量表示了波函数,应当注意,这里的向量是一个复量,而且空间维数可以是无穷,有时甚至是不可数(连续谱)。
此时态的内积可以表示为
( ψ , ψ ) = Ψ + Ψ = [ a 1 ∗ ( t ) a 2 ∗ ( t ) ⋯ a n ∗ ( t ) ⋯ ] [ a 1 ( t ) a 2 ( t ) ⋮ a n ( t ) ⋮ ] = ∑ k ∣ a k ( t ) ∣ 2 (\psi,\psi) = \Psi^+ \Psi = \begin{bmatrix} a_1^(t) & a_2^ (t) & \cdots & a_n^*(t) & \cdots \end{bmatrix} \begin{bmatrix} a_1(t) \ a_2(t) \ \vdots \ a_n(t) \ \vdots \end{bmatrix} = \sum_{k} |a_k(t)|^2 ( ψ , ψ ) = Ψ + Ψ = [ a 1 ∗ ( t ) a 2 ∗ ( t ) ⋯ a n ∗ ( t ) ⋯ ] a 1 ( t ) a 2 ( t ) ⋮ a n ( t ) ⋮ = k ∑ ∣ a k ( t ) ∣ 2
对于连续谱和多自由度情形,态 ψ \psi ψ
ψ ( x , t ) = ∑ k a k ( t ) ψ k ( x ) + ∫ a λ ( t ) ψ λ ( x ) d λ \psi(x,t) = \sum_k a_k(t)\ \psi_k(x) + \int a_\lambda(t)\ \psi_\lambda(x)\ \mathrm{d}\lambda ψ ( x , t ) = k ∑ a k ( t ) ψ k ( x ) + ∫ a λ ( t ) ψ λ ( x ) d λ
其中 a k ( t ) = ( ψ k , ψ ) , a λ ( t ) = ( ψ λ , ψ ) a_k(t) = (\psi_k,\psi),\ a_\lambda(t) = (\psi_\lambda,\psi) a k ( t ) = ( ψ k , ψ ) , a λ ( t ) = ( ψ λ , ψ ) F F F
Ψ ( t ) = [ a 1 ( t ) a 2 ( t ) ⋮ a n ( t ) ⋮ a λ ( t ) ] \Psi(t) = \begin{bmatrix} a_1(t) \ a_2(t) \ \vdots \ a_n(t) \ \vdots \ a_\lambda(t) \end{bmatrix} Ψ ( t ) = a 1 ( t ) a 2 ( t ) ⋮ a n ( t ) ⋮ a λ ( t )
这里的 a λ ( t ) a_\lambda(t) a λ ( t )
设一粒子在一维无限深方势阱
V ( x ) = { 0 , 0 < x < a ∞ , 0 < x , x > a V(x) = \begin{cases} 0, & 0<x<a \ \infty, & 0<x,x>a \end{cases} V ( x ) = { 0 , ∞ , 0 < x < a 0 < x , x > a
中运动,状态为
ψ ( x ) = 4 a cos 2 π x a sin π x a ( 0 < x < a ) \psi(x) = \frac{4}{\sqrt{a}} \cos^2\frac{\pi x}{a}\sin\frac{\pi x}{a} \kern 2em (0<x<a) ψ ( x ) = a 4 cos 2 a π x sin a π x ( 0 < x < a )
一维无限深方势阱内部的能量本征函数表示为
ψ n ( x ) = 2 a sin n π x a ( 0 < x < a , n = 1 , 2 , 3 , ⋯ ) \psi_n(x) = \sqrt{\frac{2}{a}} \sin\frac{n\pi x}{a} \kern 2em (0<x<a\ ,\ n=1,2,3,\cdots) ψ n ( x ) = a 2 sin a nπ x ( 0 < x < a , n = 1 , 2 , 3 , ⋯ )
设状态 ψ \psi ψ
ψ ( x ) = ∑ n a n ψ n ( x ) \psi(x) = \sum_n a_n\ \psi_n(x) ψ ( x ) = n ∑ a n ψ n ( x )
则展开系数
a n = ( ψ n , ψ ) = 4 2 a ∫ 0 a cos 2 π x a sin π x a sin n π x a d x = 1 2 a ∫ 0 a ( cos ( n − 1 ) π x a + cos ( n − 3 ) π x a − cos ( n + 1 ) π x a − cos ( n + 3 ) π x a ) d x = 1 2 δ 1 n + 1 2 δ 3 n = { 1 2 n = 1 , 3 0 n ≠ 1 , 3 a_n = (\psi_n,\psi) = \frac{4\sqrt{2}}{a} \int_{0}^{a} \cos^2\frac{\pi x}{a} \sin\frac{\pi x}{a} \sin\frac{n\pi x}{a} \mathrm{d}x \ \ \ = \frac{1}{\sqrt{2}a} \int_{0}^{a} \left( \cos\frac{(n-1)\pi x}{a} + \cos\frac{(n-3)\pi x}{a} - \cos\frac{(n+1)\pi x}{a} - \cos\frac{(n+3)\pi x}{a} \right) \mathrm{d}x \ \ \ = \frac{1}{\sqrt{2}}\delta_{1n} + \frac{1}{\sqrt{2}}\delta_{3n} = \begin{cases} \frac{1}{\sqrt{2}} & n=1,3 \ 0 & n \ne 1,3 \end{cases} a n = ( ψ n , ψ ) = a 4 2 ∫ 0 a cos 2 a π x sin a π x sin a nπ x d x = 2 a 1 ∫ 0 a ( cos a ( n − 1 ) π x + cos a ( n − 3 ) π x − cos a ( n + 1 ) π x − cos a ( n + 3 ) π x ) d x = 2 1 δ 1 n + 2 1 δ 3 n = { 2 1 0 n = 1 , 3 n = 1 , 3
故能量表象中的态矢量为
Ψ = [ 1 2 0 1 2 0 ⋮ 0 ⋮ ] \Psi = \begin{bmatrix} \frac{1}{\sqrt{2}} \ 0 \ \frac{1}{\sqrt{2}} \ 0 \ \vdots \ 0 \ \vdots \end{bmatrix} Ψ = 2 1 0 2 1 0 ⋮ 0 ⋮
本部分可参考《线性代数入门》 第7.5节“线性映射的矩阵表示”。
设量子态 ψ \psi ψ A ^ \hat{A} A ^ ϕ \phi ϕ
ϕ = A ^ ψ \phi = \hat{A} \psi ϕ = A ^ ψ
在以力学量完全集 F F F { ψ k ( x ) } {\psi_k(x)} { ψ k ( x )} ψ , ϕ \psi,\phi ψ , ϕ
∑ k b k ( t ) ψ k = ∑ k a k ( t ) A ^ ψ k \sum_k b_k(t)\psi_k = \sum_k a_k(t) \hat{A}\psi_k k ∑ b k ( t ) ψ k = k ∑ a k ( t ) A ^ ψ k
两边乘 ψ j ∗ \psi_j^* ψ j ∗
b j ( t ) = ∑ k a k ( t ) ( ψ j , A ^ ψ k ) = ∑ k A j k a k ( t ) b_j(t) = \sum_k a_k(t)\ (\psi_j,\hat{A}\psi_k) = \sum_k A_{jk} a_k(t) b j ( t ) = k ∑ a k ( t ) ( ψ j , A ^ ψ k ) = k ∑ A jk a k ( t )
其中 A j k = ( ψ j , A ^ ψ k ) A_{jk} = (\psi_j,\hat{A}\psi_k) A jk = ( ψ j , A ^ ψ k )
[ b 1 ( t ) b 2 ( t ) ⋮ ] = [ A 11 A 12 ⋯ A 21 A 22 ⋯ ⋮ ⋮ ⋱ ] [ a 1 ( t ) a 2 ( t ) ⋮ ] \begin{bmatrix} b_1(t) \ b_2(t) \ \vdots \ \end{bmatrix} = \begin{bmatrix} A_{11} & A_{12} & \cdots \ A_{21} & A_{22} & \cdots \ \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1(t) \ a_2(t) \ \vdots \ \end{bmatrix} b 1 ( t ) b 2 ( t ) ⋮ = A 11 A 21 ⋮ A 12 A 22 ⋮ ⋯ ⋯ ⋱ a 1 ( t ) a 2 ( t ) ⋮
记其中的矩阵为 A A A
Φ ( t ) = A Ψ ( t ) \Phi(t) = A \Psi(t) Φ ( t ) = A Ψ ( t )
表示力学量算符 A ^ \hat{A} A ^ 厄米矩阵 (取转置再取复共轭后不变),即 A m n = A n m ∗ = A m n + A_{mn} = A^*{nm} = A^+ {mn} A mn = A nm ∗ = A mn +
A m n = ( ψ m , A ^ ψ n ) = ( A ^ ψ m , ψ n ) = ( ψ n , A ^ ψ m ) ∗ = A n m ∗ A_{mn} = (\psi_m,\hat{A}\psi_n) = (\hat{A}\psi_m,\psi_n) = (\psi_n,\hat{A}\psi_m)^* = A^*_{nm} A mn = ( ψ m , A ^ ψ n ) = ( A ^ ψ m , ψ n ) = ( ψ n , A ^ ψ m ) ∗ = A nm ∗
特别的,在自身表象下, A A A 对角 的厄米矩阵,且各对角元素就是 A ^ \hat{A} A ^ 本征值 ,证明如下:
A m n = ( ψ m , A ^ ψ n ) = ( ψ m , A n ψ n ) = A n ( ψ m , ψ n ) = A n δ m n A_{mn} = (\psi_m,\hat{A}\psi_n) = (\psi_m,A_n\psi_n) = A_n(\psi_m,\psi_n) = A_n\delta_{mn} A mn = ( ψ m , A ^ ψ n ) = ( ψ m , A n ψ n ) = A n ( ψ m , ψ n ) = A n δ mn
对于一维谐振子,可利用Hermite多项式的递推关系求得
x ^ ψ n = 1 α [ n + 1 2 ψ n + 1 + n 2 ψ n − 1 ] p ^ ψ n = i ℏ α [ n + 1 2 ψ n + 1 − n 2 ψ n − 1 ] H ^ ψ n = ( n + 1 2 ) ℏ ω ψ n \hat{x}\psi_n = \frac{1}{\alpha} \left[ \sqrt{\frac{n+1}{2}} \psi_{n+1} + \sqrt{\frac{n}{2}} \psi_{n-1} \right] \ \ \ \hat{p}\psi_n = \mathrm{i}\hbar\alpha \left[ \sqrt{\frac{n+1}{2}} \psi_{n+1} - \sqrt{\frac{n}{2}} \psi_{n-1} \right] \ \ \ \hat{H}\psi_n = \left( n + \frac12 \right) \hbar\omega \psi_n x ^ ψ n = α 1 [ 2 n + 1 ψ n + 1 + 2 n ψ n − 1 ] p ^ ψ n = i ℏ α [ 2 n + 1 ψ n + 1 − 2 n ψ n − 1 ] H ^ ψ n = ( n + 2 1 ) ℏ ω ψ n
故可得矩阵元的表达式(注意 m , n = 0 , 1 , 2 , 3 , ⋯ m,n = 0,1,2,3,\cdots m , n = 0 , 1 , 2 , 3 , ⋯
x m n = 1 α [ n + 1 2 δ m , n + 1 + n 2 δ m , n − 1 ] p m n = i ℏ α [ n + 1 2 δ m , n + 1 − n 2 δ m , n − 1 ] H m n = ( n + 1 2 ) ℏ ω δ m n x_{mn} = \frac{1}{\alpha} \left[ \sqrt{\frac{n+1}{2}} \delta_{m,n+1} + \sqrt{\frac{n}{2}} \delta_{m,n-1} \right] \ \ \ p_{mn} = \mathrm{i}\hbar\alpha \left[ \sqrt{\frac{n+1}{2}} \delta_{m,n+1} - \sqrt{\frac{n}{2}} \delta_{m,n-1} \right] \ \ \ H_{mn} = \left( n + \frac12 \right) \hbar\omega \delta_{mn} x mn = α 1 [ 2 n + 1 δ m , n + 1 + 2 n δ m , n − 1 ] p mn = i ℏ α [ 2 n + 1 δ m , n + 1 − 2 n δ m , n − 1 ] H mn = ( n + 2 1 ) ℏ ω δ mn
则能量表象中坐标 x x x p p p H H H
( x m n ) = 1 α [ 0 1 / 2 0 0 ⋯ 1 / 2 0 2 / 2 0 ⋯ 0 2 / 2 0 3 / 2 ⋯ 0 0 3 / 2 0 ⋯ ⋮ ⋮ ⋮ ⋮ ⋱ ] (x_{mn}) = \frac{1}{\alpha} \begin{bmatrix} 0 & \sqrt{1/2} & 0 & 0 & \cdots \ \sqrt{1/2} & 0 & \sqrt{2/2} & 0 & \cdots \ 0 & \sqrt{2/2} & 0 & \sqrt{3/2} & \cdots \ 0 & 0 & \sqrt{3/2} & 0 & \cdots \ \vdots & \vdots & \vdots & \vdots & \ddots \ \end{bmatrix} ( x mn ) = α 1 0 1/2 0 0 ⋮ 1/2 0 2/2 0 ⋮ 0 2/2 0 3/2 ⋮ 0 0 3/2 0 ⋮ ⋯ ⋯ ⋯ ⋯ ⋱
( p m n ) = i ℏ α [ 0 − 1 / 2 0 0 ⋯ 1 / 2 0 − 2 / 2 0 ⋯ 0 2 / 2 0 − 3 / 2 ⋯ 0 0 3 / 2 0 ⋯ ⋮ ⋮ ⋮ ⋮ ⋱ ] (p_{mn}) = \mathrm{i}\hbar\alpha \begin{bmatrix} 0 & -\sqrt{1/2} & 0 & 0 & \cdots \ \sqrt{1/2} & 0 & -\sqrt{2/2} & 0 & \cdots \ 0 & \sqrt{2/2} & 0 & -\sqrt{3/2} & \cdots \ 0 & 0 & \sqrt{3/2} & 0 & \cdots \ \vdots & \vdots & \vdots & \vdots & \ddots \ \end{bmatrix} ( p mn ) = i ℏ α 0 1/2 0 0 ⋮ − 1/2 0 2/2 0 ⋮ 0 − 2/2 0 3/2 ⋮ 0 0 − 3/2 0 ⋮ ⋯ ⋯ ⋯ ⋯ ⋱
( H m n ) = ℏ ω [ 1 / 2 0 0 0 ⋯ 0 3 / 2 0 0 ⋯ 0 0 5 / 2 0 ⋯ 0 0 0 7 / 2 ⋯ ⋮ ⋮ ⋮ ⋮ ⋱ ] (H_{mn}) = \hbar\omega \begin{bmatrix} 1/2 & 0 & 0 & 0 & \cdots \ 0 & 3/2 & 0 & 0 & \cdots \ 0 & 0 & 5/2 & 0 & \cdots \ 0 & 0 & 0 & 7/2 & \cdots \ \vdots & \vdots & \vdots & \vdots & \ddots \ \end{bmatrix} ( H mn ) = ℏ ω 1/2 0 0 0 ⋮ 0 3/2 0 0 ⋮ 0 0 5/2 0 ⋮ 0 0 0 7/2 ⋮ ⋯ ⋯ ⋯ ⋯ ⋱
本小节在考试中不涉及
考虑两组对易力学量完全集 F , F ′ F,F' F , F ′ { ψ k } , { ψ α ′ } {\psi_k},{\psi'_\alpha} { ψ k } , { ψ α ′ } ψ \psi ψ
ψ = ∑ k a k ψ k = ∑ α a α ′ ψ α ′ \psi = \sum_k a_k\psi_k = \sum_\alpha a'\alpha\psi' \alpha ψ = k ∑ a k ψ k = α ∑ a α ′ ψ α ′
同乘 ψ α ′ ∗ \psi'^*_\alpha ψ α ′ ∗
a α ′ = ∑ k a k ( ψ α ′ , ψ k ) = ∑ k S α k a k a'\alpha = \sum_k a_k(\psi' \alpha,\psi_k) = \sum_k S_{\alpha k} a_k a α ′ = k ∑ a k ( ψ α ′ , ψ k ) = k ∑ S α k a k
其中 S α k = ( ψ a ′ , ψ k ) S_{\alpha k } = (\psi'_a,\psi_k) S α k = ( ψ a ′ , ψ k )
[ a 1 ′ a 2 ′ ⋮ ] = [ S 11 S 12 ⋯ S 21 S 22 ⋯ ⋮ ⋮ ⋱ ] [ a 1 a 2 ⋮ ] \begin{bmatrix} a'1 \ a'2 \ \vdots \ \end{bmatrix} = \begin{bmatrix} S {11} & S {12} & \cdots \ S_{21} & S_{22} & \cdots \ \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1 \ a_2 \ \vdots \ \end{bmatrix} a 1 ′ a 2 ′ ⋮ = S 11 S 21 ⋮ S 12 S 22 ⋮ ⋯ ⋯ ⋱ a 1 a 2 ⋮
记其中的矩阵为 S S S a ′ = S a a'=Sa a ′ = S a S S S
S S + = S + S = I SS^+ = S^+S = I S S + = S + S = I
考虑两组对易力学量完全集 F , F ′ F,F' F , F ′ { ψ k } , { ψ α ′ } {\psi_k},{\psi'\alpha} { ψ k } , { ψ α ′ } F F F A ^ \hat{A} A ^ ( A k j ) (A{kj}) ( A kj ) A k j = ( ψ k , A ^ ψ j ) A_{kj} = (\psi_k,\hat{A}\psi_j) A kj = ( ψ k , A ^ ψ j ) F ′ F' F ′ A ^ \hat{A} A ^ ( A α β ′ ) (A'_{\alpha\beta}) ( A α β ′ )
A α β ′ = ( ψ α ′ , A ^ ψ β ′ ) = ( ∑ k ( ψ k , ψ α ′ ) ψ k , A ^ ∑ j ( ψ j , ψ β ′ ) ψ j ) = ( ∑ k S α k ∗ ψ k , A ^ ∑ j S β j ∗ ψ j ) = ∑ k j S α k ( ψ k , A ^ ψ j ) S β j ∗ = ∑ k j S α k A k j S j β + = ( S A S + ) α β A'{\alpha\beta} = (\psi' \alpha,\hat{A}\psi'\beta) = (\sum {k} (\psi_k,\psi'\alpha)\psi_k ,\hat{A} \sum {j} (\psi_j,\psi'\beta)\psi_j) = (\sum {k} S^{\alpha k}\psi_k ,\hat{A} \sum {j} S^{\beta j}\psi_j) \ \ \ = \sum {kj} S_{\alpha k} (\psi_k , \hat{A}\psi_j) S^*{\beta j} = \sum {kj} S_{\alpha k} A_{kj} S^+{j\beta} = (SAS^+) {\alpha\beta} A α β ′ = ( ψ α ′ , A ^ ψ β ′ ) = ( k ∑ ( ψ k , ψ α ′ ) ψ k , A ^ j ∑ ( ψ j , ψ β ′ ) ψ j ) = ( k ∑ S α k ∗ ψ k , A ^ j ∑ S β j ∗ ψ j ) = kj ∑ S α k ( ψ k , A ^ ψ j ) S β j ∗ = kj ∑ S α k A kj S j β + = ( S A S + ) α β
即
A ′ = S A S + = S A S − A' = SAS^+ = SAS^- A ′ = S A S + = S A S −
经过表象变换后,力学量算符的本征值不改变,本征函数可能发生变化。
i ℏ ∂ ∂ t ψ ( x , t ) = H ^ ψ ( x , t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(x,t) = \hat{H} \psi(x,t) i ℏ ∂ t ∂ ψ ( x , t ) = H ^ ψ ( x , t )
在 F F F ψ ( x , t ) \psi(x,t) ψ ( x , t )
ψ ( x , t ) = ∑ k a k ( t ) ψ k ( x ) \psi(x,t) = \sum_k a_k(t)\ \psi_k(x) ψ ( x , t ) = k ∑ a k ( t ) ψ k ( x )
代入Schrödinger方程可得
i ℏ ∑ k a k ′ ( t ) ψ k ( x ) = ∑ k a k ( t ) H ^ ψ k ( x ) \mathrm{i}\hbar \sum_k a'_k(t)\ \psi_k(x) = \sum_k a_k(t) \hat{H} \psi_k(x) i ℏ k ∑ a k ′ ( t ) ψ k ( x ) = k ∑ a k ( t ) H ^ ψ k ( x )
两边同乘 ψ j ∗ \psi^*_j ψ j ∗
i ℏ a j ′ ( t ) = ∑ k H j k a k ( t ) , H j k = ( ψ j , H ^ ψ k ) \mathrm{i}\hbar a'j(t) = \sum_k H {jk} a_k(t)\ , \kern 2em H_{jk} = (\psi_j,\hat{H}\psi_k) i ℏ a j ′ ( t ) = k ∑ H jk a k ( t ) , H jk = ( ψ j , H ^ ψ k )
表示成矩阵形式即为
i ℏ [ a 1 ′ ( t ) a 2 ′ ( t ) ⋮ ] = [ H 11 H 12 ⋯ H 21 H 22 ⋯ ⋮ ⋮ ⋱ ] [ a 1 ( t ) a 2 ( t ) ⋮ ] \mathrm{i}\hbar \begin{bmatrix} a'1(t) \ a'2(t) \ \vdots \ \end{bmatrix} = \begin{bmatrix} H {11} & H {12} & \cdots \ H_{21} & H_{22} & \cdots \ \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1(t) \ a_2(t) \ \vdots \ \end{bmatrix} i ℏ a 1 ′ ( t ) a 2 ′ ( t ) ⋮ = H 11 H 21 ⋮ H 12 H 22 ⋮ ⋯ ⋯ ⋱ a 1 ( t ) a 2 ( t ) ⋮
简记为
i ℏ d Ψ d t = H Ψ \mathrm{i} \hbar \frac{\mathrm{d}\Psi}{\mathrm{d}t} = H \Psi i ℏ d t d Ψ = H Ψ
在量子态 ψ \psi ψ A ^ \hat{A} A ^
A ˉ = ( ψ , A ^ ψ ) = ( ∑ k a k ψ k , ∑ j a j A ^ ψ j ) = ∑ k j a k ∗ ( ψ k , A ^ ψ j ) a j = ∑ k j a k ∗ A k j a j = [ a 1 ∗ a 2 ∗ ⋯ ] [ A 11 A 12 ⋯ A 21 A 22 ⋯ ⋮ ⋮ ⋱ ] [ a 1 a 2 ⋮ ] \bar{A} = (\psi,\hat{A}\psi) = (\sum_k a_k\psi_k,\sum_j a_j\hat{A}\psi_j) = \sum_{kj} a^k (\psi_k,\hat{A}\psi_j) a_j = \sum {kj} a^k A {kj} a_j \ \ \ = \begin{bmatrix} a^_1 & a^ 2 & \cdots \end{bmatrix} \begin{bmatrix} A {11} & A_{12} & \cdots \ A_{21} & A_{22} & \cdots \ \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1 \ a_2 \ \vdots \ \end{bmatrix} A ˉ = ( ψ , A ^ ψ ) = ( k ∑ a k ψ k , j ∑ a j A ^ ψ j ) = kj ∑ a k ∗ ( ψ k , A ^ ψ j ) a j = kj ∑ a k ∗ A kj a j = [ a 1 ∗ a 2 ∗ ⋯ ] A 11 A 21 ⋮ A 12 A 22 ⋮ ⋯ ⋯ ⋱ a 1 a 2 ⋮
简记为
A ˉ = Ψ + A Ψ \bar{A} = \Psi^+ A \Psi A ˉ = Ψ + A Ψ
算符 A ^ \hat{A} A ^
A ^ ψ = λ ψ \hat{A} \psi = \lambda \psi A ^ ψ = λ ψ
其中 λ \lambda λ F F F ψ \psi ψ
∑ k a k A ^ ψ k = λ ∑ k a k ψ k \sum_{k} a_k \hat{A} \psi_k = \lambda \sum_k a_k \psi_k k ∑ a k A ^ ψ k = λ k ∑ a k ψ k
两边同乘 ψ j ∗ \psi^*_j ψ j ∗
∑ k ( ψ j , A ^ ψ k ) a k = ∑ k A j k a k = λ a j \sum_{k} (\psi_j,\hat{A} \psi_k) a_k = \sum_{k} A_{jk} a_k = \lambda a_j k ∑ ( ψ j , A ^ ψ k ) a k = k ∑ A jk a k = λ a j
表示成矩阵形式即为
[ A 11 A 12 ⋯ A 21 A 22 ⋯ ⋮ ⋮ ⋱ ] [ a 1 a 2 ⋮ ] = λ [ a 1 a 2 ⋮ ] ⇓ [ A 11 − λ A 12 ⋯ A 21 A 22 − λ ⋯ ⋮ ⋮ ⋱ ] [ a 1 a 2 ⋮ ] = 0 ⃗ \begin{bmatrix} A_{11} & A_{12} & \cdots \ A_{21} & A_{22} & \cdots \ \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1 \ a_2 \ \vdots \ \end{bmatrix} = \lambda \begin{bmatrix} a_1 \ a_2 \ \vdots \ \end{bmatrix} \ \Downarrow \ \begin{bmatrix} A_{11}-\lambda & A_{12} & \cdots \ A_{21} & A_{22}-\lambda & \cdots \ \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1 \ a_2 \ \vdots \ \end{bmatrix} = \vec{0} A 11 A 21 ⋮ A 12 A 22 ⋮ ⋯ ⋯ ⋱ a 1 a 2 ⋮ = λ a 1 a 2 ⋮ ⇓ A 11 − λ A 21 ⋮ A 12 A 22 − λ ⋮ ⋯ ⋯ ⋱ a 1 a 2 ⋮ = 0
简记为
( A − λ I ) Ψ = 0 (A - \lambda I) \Psi = 0 ( A − λ I ) Ψ = 0
为了使此关于 Ψ \Psi Ψ ( A − λ I ) (A-\lambda I) ( A − λ I )
det ( A − λ I ) = 0 \det (A-\lambda I) = 0 det ( A − λ I ) = 0
如果 A A A N × N N \times N N × N λ \lambda λ N N N N N N { λ 1 , λ 2 , ⋯ , λ N } {\lambda_1,\lambda_2,\cdots,\lambda_N} { λ 1 , λ 2 , ⋯ , λ N } 本征值 ,代回方程 ( A − λ I ) Ψ = 0 (A-\lambda I)\Psi=0 ( A − λ I ) Ψ = 0 本征函数 Ψ \Psi Ψ
若方程 det ( A − λ I ) = 0 \det (A-\lambda I) = 0 det ( A − λ I ) = 0
同一状态在不同的量子力学表象中所表达的物理内容完全相同,为了更为简便的表示,可以使用Dirac符号,它是一种与表象无关的符号体系。
量子体系的一切可能状态构成一个Hilbert空间,空间中的一个矢量(一般为复量)用以标记一个量子态,用一个右矢 ∣ ⟩ |\ \rangle ∣ ⟩ ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ ψ \psi ψ 本征值 (或对应的量子数 )标在右矢内,例如: ∣ x ′ ⟩ | x' \rangle ∣ x ′ ⟩ x ′ x' x ′ ∣ p ′ ⟩ | p' \rangle ∣ p ′ ⟩ p ′ p' p ′ ∣ E n ⟩ | E_n \rangle ∣ E n ⟩ ∣ n ⟩ | n \rangle ∣ n ⟩ E n E_n E n n n n ∣ l m ⟩ | lm \rangle ∣ l m ⟩ ( L 2 , L z ) (L^2,L_z) ( L 2 , L z ) l ( l + 1 ) ℏ l(l+1)\hbar l ( l + 1 ) ℏ m ℏ m\hbar m ℏ
态的上述表示,都只是一个抽象的态矢,未涉及任何具体的表象。这体现了在任何表象下,本征值都是相同的,(而本征函数可能会不同),而对于一个对易力学量完全集,使用一组量子数表示的一组本征值就可以唯一确定本征态。
左矢 ⟨ ∣ \langle \ | ⟨ ∣ ∣ ⟩ | \ \rangle ∣ ⟩ ⟨ ψ ∣ = ∣ ψ ⟩ + \langle \psi | = | \psi \rangle^+ ⟨ ψ ∣ = ∣ ψ ⟩ + ∣ ψ ⟩ = C 1 ∣ ϕ 1 ⟩ + C 2 ∣ ϕ 2 ⟩ | \psi \rangle = C_1\ | \phi_1 \rangle + C_2\ | \phi_2 \rangle ∣ ψ ⟩ = C 1 ∣ ϕ 1 ⟩ + C 2 ∣ ϕ 2 ⟩ ⟨ ψ ∣ = C 1 ∗ ⟨ ϕ 1 ∣ + C 2 ∗ ⟨ ϕ 2 ∣ \langle \psi | = C_1^\ \langle \phi_1 | + C_2^ \langle \phi_2 | ⟨ ψ ∣ = C 1 ∗ ⟨ ϕ 1 ∣ + C 2 ∗ ⟨ ϕ 2 ∣
借助线性代数的角度来看,右矢为列向量,而左矢为取复共轭后的行向量。
态矢 ⟨ ϕ ∣ \langle \phi | ⟨ ϕ ∣ ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ ( ϕ , ψ ) = ⟨ ϕ ∣ ∣ ψ ⟩ = ⟨ ϕ ∣ ψ ⟩ (\phi,\psi) = \langle \phi || \psi \rangle = \langle \phi | \psi \rangle ( ϕ , ψ ) = ⟨ ϕ ∣∣ ψ ⟩ = ⟨ ϕ ∣ ψ ⟩ ( ψ , ϕ ) = ( ϕ , ψ ) ∗ = ⟨ ϕ ∣ ψ ⟩ ∗ = ⟨ ψ ∣ ϕ ⟩ (\psi,\phi)=(\phi,\psi)^* = \langle \phi | \psi \rangle^* = \langle \psi | \phi \rangle ( ψ , ϕ ) = ( ϕ , ψ ) ∗ = ⟨ ϕ ∣ ψ ⟩ ∗ = ⟨ ψ ∣ ϕ ⟩
若 ⟨ ϕ ∣ ψ ⟩ = 0 \langle \phi | \psi \rangle = 0 ⟨ ϕ ∣ ψ ⟩ = 0 ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ ∣ ϕ ⟩ | \phi \rangle ∣ ϕ ⟩ 正交 ;若 ⟨ ψ ∣ ψ ⟩ = 1 \langle \psi | \psi \rangle = 1 ⟨ ψ ∣ ψ ⟩ = 1 ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ 归一 化态矢。
设力学量完全集 F F F ∣ k ⟩ | k \rangle ∣ k ⟩ 正交归一性 表示为
⟨ k ∣ j ⟩ = δ k j \langle k | j \rangle = \delta_{kj} ⟨ k ∣ j ⟩ = δ kj
对于连续谱,如坐标本征态,正交归一性表示为
⟨ x ′ ∣ x ′ ′ ⟩ = δ ( x ′ − x ′ ′ ) \langle x' | x'' \rangle = \delta(x'-x'') ⟨ x ′ ∣ x ′′ ⟩ = δ ( x ′ − x ′′ )
算符对右矢向右作用仍为一个右矢,对左矢向左作用仍为一个左矢,即
⟨ ϕ ∣ A ^ ∣ ψ ⟩ = ⟨ ϕ ∣ [ A ^ ∣ ψ ⟩ ] = ⟨ ϕ ∣ A ^ ψ ⟩ ⟨ ϕ ∣ A ^ ∣ ψ ⟩ = [ ⟨ ϕ ∣ A ^ ] ∣ ψ ⟩ = ⟨ A ^ + ϕ ∣ ψ ⟩ \langle \phi | \hat{A} | \psi \rangle = \langle \phi | \left[ \hat{A} | \psi \rangle \right] = \langle \phi | \hat{A} \psi \rangle \ \langle \phi | \hat{A} | \psi \rangle = \left[ \langle \phi | \hat{A} \right] | \psi \rangle = \langle \hat{A}^+ \phi | \psi \rangle ⟨ ϕ ∣ A ^ ∣ ψ ⟩ = ⟨ ϕ ∣ [ A ^ ∣ ψ ⟩ ] = ⟨ ϕ ∣ A ^ ψ ⟩ ⟨ ϕ ∣ A ^ ∣ ψ ⟩ = [ ⟨ ϕ ∣ A ^ ] ∣ ψ ⟩ = ⟨ A ^ + ϕ ∣ ψ ⟩
注:若 A ^ \hat{A} A ^ ⟨ A ^ ϕ ∣ ψ ⟩ \langle \hat{A} \phi | \psi \rangle ⟨ A ^ ϕ ∣ ψ ⟩
力学量 A A A
A ^ ∣ ψ ⟩ = A ′ ∣ ψ ⟩ \hat{A} | \psi \rangle = A' | \psi \rangle A ^ ∣ ψ ⟩ = A ′ ∣ ψ ⟩
其中 A ′ A' A ′ ψ \psi ψ
力学量 A A A
A ˉ = ( ψ , A ^ ψ ) ( ψ , ψ ) = ⟨ ψ ∣ A ^ ∣ ψ ⟩ ⟨ ψ ∣ ψ ⟩ \bar{A} = \frac{(\psi,\hat{A}\psi)}{(\psi,\psi)} = \frac{\langle \psi | \hat{A} | \psi \rangle}{\langle \psi | \psi \rangle} A ˉ = ( ψ , ψ ) ( ψ , A ^ ψ ) = ⟨ ψ ∣ ψ ⟩ ⟨ ψ ∣ A ^ ∣ ψ ⟩
设在 F F F ∣ k ⟩ | k \rangle ∣ k ⟩ ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ ∣ k ⟩ | k \rangle ∣ k ⟩
∣ ψ ⟩ = ∑ k a k ∣ k ⟩ | \psi \rangle = \sum_k a_k | k \rangle ∣ ψ ⟩ = k ∑ a k ∣ k ⟩
展开系数
a k = ( ψ k , ψ ) = ⟨ k ∣ ψ ⟩ a_k = (\psi_k,\psi) = \langle k | \psi \rangle a k = ( ψ k , ψ ) = ⟨ k ∣ ψ ⟩
代入可得
∣ ψ ⟩ = ∑ k ⟨ k ∣ ψ ⟩ ∣ k ⟩ = ∑ k ∣ k ⟩ ⟨ k ∣ ψ ⟩ | \psi \rangle = \sum_k \langle k | \psi \rangle | k \rangle = \sum_k | k \rangle \langle k | \psi \rangle ∣ ψ ⟩ = k ∑ ⟨ k ∣ ψ ⟩ ∣ k ⟩ = k ∑ ∣ k ⟩ ⟨ k ∣ ψ ⟩
式中 ∣ k ⟩ ⟨ k ∣ | k \rangle \langle k | ∣ k ⟩ ⟨ k ∣ 投影算符
P ^ k = ∣ k ⟩ ⟨ k ∣ \hat{P}_k = | k \rangle \langle k | P ^ k = ∣ k ⟩ ⟨ k ∣
它对任何态矢 ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ ∣ k ⟩ | k \rangle ∣ k ⟩
P ^ k ∣ ψ ⟩ = ∣ k ⟩ ⟨ k ∣ ψ ⟩ = a k ∣ k ⟩ \hat{P}_k | \psi \rangle = | k \rangle \langle k | \psi \rangle = a_k | k \rangle P ^ k ∣ ψ ⟩ = ∣ k ⟩ ⟨ k ∣ ψ ⟩ = a k ∣ k ⟩
根据 ∣ ψ ⟩ = ∑ k ∣ k ⟩ ⟨ k ∣ ψ ⟩ | \psi \rangle = \sum_k | k \rangle \langle k | \psi \rangle ∣ ψ ⟩ = ∑ k ∣ k ⟩ ⟨ k ∣ ψ ⟩ 封闭关系
∑ k ∣ k ⟩ ⟨ k ∣ = I \sum_k | k \rangle \langle k | = I k ∑ ∣ k ⟩ ⟨ k ∣ = I
这正是这一组基矢 ∣ k ⟩ | k \rangle ∣ k ⟩
∫ d x ′ ∣ x ′ ⟩ ⟨ x ′ ∣ = I \int \mathrm{d}x'\ | x' \rangle \langle x' | = I ∫ d x ′ ∣ x ′ ⟩ ⟨ x ′ ∣ = I
态 ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩ { ∣ x 0 ⟩ : − ∞ < x 0 < + ∞ } { | x_0 \rangle : -\infty < x_0 < +\infty} { ∣ x 0 ⟩ : − ∞ < x 0 < + ∞ }
∣ ψ ⟩ = ∫ − ∞ + ∞ d x 0 ∣ x 0 ⟩ ⟨ x 0 ∣ ψ ⟩ | \psi \rangle = \int_{-\infty}^{+\infty} \mathrm{d}x_0 | x_0 \rangle \langle x_0 | \psi \rangle ∣ ψ ⟩ = ∫ − ∞ + ∞ d x 0 ∣ x 0 ⟩ ⟨ x 0 ∣ ψ ⟩
在坐标表象下,本征函数为 δ ( x − x 0 ) \delta(x-x_0) δ ( x − x 0 )
ψ ( x ) = ∫ − ∞ + ∞ C ( x 0 ) δ ( x − x 0 ) d x 0 = C ( x ) \psi (x) = \int_{-\infty}^{+\infty} C(x_0)\ \delta(x-x_0)\ \mathrm{d}x_0 = C(x) ψ ( x ) = ∫ − ∞ + ∞ C ( x 0 ) δ ( x − x 0 ) d x 0 = C ( x )
其中展开系数
C ( x 0 ) = ⟨ x 0 ∣ ψ ⟩ C(x_0) = \langle x_0 | \psi \rangle C ( x 0 ) = ⟨ x 0 ∣ ψ ⟩
两式结合可以得到
ψ ( x ) = ⟨ x ∣ ψ ⟩ \psi(x) = \langle x | \psi \rangle ψ ( x ) = ⟨ x ∣ ψ ⟩
事实上,这个式子对任意表象都是成立的,即在力学量 A A A ψ ( A ) = ⟨ A ∣ ψ ⟩ \psi(A) = \langle A | \psi \rangle ψ ( A ) = ⟨ A ∣ ψ ⟩
故坐标在本征值 x 0 x_0 x 0
⟨ x ∣ x 0 ⟩ = δ ( x − x 0 ) \langle x | x_0 \rangle = \delta(x-x_0) ⟨ x ∣ x 0 ⟩ = δ ( x − x 0 )
动量在本征值 p 0 p_0 p 0
⟨ x ∣ p 0 ⟩ = 1 2 π ℏ e i ℏ p 0 x \langle x | p_0 \rangle = \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p_0x} ⟨ x ∣ p 0 ⟩ = 2 π ℏ 1 e ℏ i p 0 x
ψ ( p ) = ⟨ p ∣ ψ ⟩ \psi(p) = \langle p | \psi \rangle ψ ( p ) = ⟨ p ∣ ψ ⟩
坐标在本征值 x 0 x_0 x 0
⟨ p ∣ x 0 ⟩ = 1 2 π ℏ e − i ℏ p x 0 \langle p | x_0 \rangle = \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}px_0} ⟨ p ∣ x 0 ⟩ = 2 π ℏ 1 e − ℏ i p x 0
动量在本征值 p 0 p_0 p 0
⟨ p ∣ p 0 ⟩ = δ ( p − p 0 ) \langle p | p_0 \rangle = \delta(p-p_0) ⟨ p ∣ p 0 ⟩ = δ ( p − p 0 )
在本小节中主要是给出一些例子。
坐标 x ^ \hat{x} x ^
( x ) x ′ x ′ ′ = ⟨ x ′ ∣ x ^ ∣ x ′ ′ ⟩ = [ ⟨ x ′ ∣ x ^ ] x ′ ′ ⟩ = x ′ ⟨ x ′ ∣ x ′ ′ ⟩ = x ′ δ ( x ′ − x ′ ′ ) (x)_{x'x''} = \langle x' | \hat{x} | x'' \rangle = \left[ \langle x' | \hat{x} \right] x'' \rangle = x' \langle x' | x'' \rangle = x' \delta(x'-x'') ( x ) x ′ x ′′ = ⟨ x ′ ∣ x ^ ∣ x ′′ ⟩ = [ ⟨ x ′ ∣ x ^ ] x ′′ ⟩ = x ′ ⟨ x ′ ∣ x ′′ ⟩ = x ′ δ ( x ′ − x ′′ )
动量 p ^ \hat{p} p ^
( p ) x ′ x ′ ′ = ⟨ x ′ ∣ p ^ ∣ x ′ ′ ⟩ = ∫ ∫ d p ′ d p ′ ′ ⟨ x ′ ∣ p ′ ⟩ ⟨ p ′ ∣ p ^ ∣ p ′ ′ ⟩ ⟨ p ′ ′ ∣ x ′ ′ ⟩ = ∫ ∫ d p ′ d p ′ ′ 1 2 π ℏ e i ℏ p ′ x ′ p ′ δ ( p ′ − p ′ ′ ) 1 2 π ℏ e − i ℏ p ′ ′ x ′ ′ = 1 2 π ℏ ∫ d p ′ p ′ e i ℏ p ′ ( x ′ − x ′ ′ ) = 1 2 π ℏ ∫ d p ′ ( − i ℏ ∂ ∂ x ′ ) e i ℏ p ′ ( x ′ − x ′ ′ ) = − i ℏ ∂ ∂ x ′ 1 2 π ℏ ∫ d p ′ e i ℏ p ′ ( x ′ − x ′ ′ ) = − i ℏ ∂ ∂ x ′ δ ( x ′ − x ′ ′ ) (p)_{x'x''} = \langle x' | \hat{p} | x'' \rangle = \int \int \mathrm{d}p'\ \mathrm{d}p''\ \langle x' | p' \rangle\ \langle p' | \hat{p} | p'' \rangle\ \langle p'' | x'' \rangle \ \ \ = \int \int \mathrm{d}p'\ \mathrm{d}p''\ \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'x'}\ p' \delta(p'-p'')\ \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}p''x''} \ \ \ = \frac{1}{2\pi\hbar} \int \mathrm{d}p'\ p'\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'(x'-x'')} \ \ \ = \frac{1}{2\pi\hbar} \int \mathrm{d}p' \left(-\mathrm{i}\hbar \frac{\partial}{\partial x'} \right) \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'(x'-x'')} \ \ \ = -\mathrm{i}\hbar \frac{\partial}{\partial x'} \frac{1}{2\pi\hbar} \int \mathrm{d}p'\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'(x'-x'')} \ \ \ = -\mathrm{i}\hbar \frac{\partial}{\partial x'} \delta(x'-x'') ( p ) x ′ x ′′ = ⟨ x ′ ∣ p ^ ∣ x ′′ ⟩ = ∫∫ d p ′ d p ′′ ⟨ x ′ ∣ p ′ ⟩ ⟨ p ′ ∣ p ^ ∣ p ′′ ⟩ ⟨ p ′′ ∣ x ′′ ⟩ = ∫∫ d p ′ d p ′′ 2 π ℏ 1 e ℏ i p ′ x ′ p ′ δ ( p ′ − p ′′ ) 2 π ℏ 1 e − ℏ i p ′′ x ′′ = 2 π ℏ 1 ∫ d p ′ p ′ e ℏ i p ′ ( x ′ − x ′′ ) = 2 π ℏ 1 ∫ d p ′ ( − i ℏ ∂ x ′ ∂ ) e ℏ i p ′ ( x ′ − x ′′ ) = − i ℏ ∂ x ′ ∂ 2 π ℏ 1 ∫ d p ′ e ℏ i p ′ ( x ′ − x ′′ ) = − i ℏ ∂ x ′ ∂ δ ( x ′ − x ′′ )
哈密顿量 H ^ \hat{H} H ^
( H ) x ′ x ′ ′ = ⟨ x ′ ∣ H ^ ∣ x ′ ′ ⟩ = 1 2 m ⟨ x ′ ∣ p ^ 2 ∣ x ′ ′ ⟩ + ⟨ x ′ ∣ V ^ ∣ x ′ ′ ⟩ = 1 2 m ∫ ∫ d p ′ d p ′ ′ ⟨ x ′ ∣ p ′ ⟩ ⟨ p ′ ∣ p ^ 2 ∣ p ′ ′ ⟩ ⟨ p ′ ′ ∣ x ′ ′ ⟩ + ⟨ x ′ ∣ V ( x ) ∣ x ′ ′ ⟩ = 1 2 m ∫ ∫ d p ′ d p ′ ′ 1 2 π ℏ e i ℏ p ′ x ′ p ′ 2 δ ( p ′ − p ′ ′ ) 1 2 π ℏ e − i ℏ p ′ ′ x ′ ′ + V ( x ′ ) ⟨ x ′ ∣ x ′ ′ ⟩ = 1 2 m 1 2 π ℏ ∫ d p ′ p ′ 2 e i ℏ p ′ ( x ′ − x ′ ′ ) + V ( x ′ ) δ ( x ′ − x ′ ′ ) = 1 2 m 1 2 π ℏ ∫ d p ′ ( − ℏ 2 ∂ 2 ∂ 2 x ′ ) e i ℏ p ′ ( x ′ − x ′ ′ ) + V ( x ′ ) δ ( x ′ − x ′ ′ ) = − ℏ 2 2 m ∂ 2 ∂ 2 x ′ 1 2 π ℏ ∫ d p ′ e i ℏ p ′ ( x ′ − x ′ ′ ) + V ( x ′ ) δ ( x ′ − x ′ ′ ) = − ℏ 2 2 m ∂ 2 ∂ x ′ 2 δ ( x ′ − x ′ ′ ) + V ( x ′ ) δ ( x ′ − x ′ ′ ) (H)_{x'x''} = \langle x' | \hat{H} | x'' \rangle = \frac{1}{2m} \langle x' | \hat{p}^2 | x'' \rangle + \langle x' | \hat{V} | x'' \rangle \ \ \ = \frac{1}{2m} \int \int \mathrm{d}p'\ \mathrm{d}p''\ \langle x' | p' \rangle\ \langle p' | \hat{p}^2 | p'' \rangle\ \langle p'' | x'' \rangle + \langle x' | V(x) | x'' \rangle \ \ \ = \frac{1}{2m} \int \int \mathrm{d}p'\ \mathrm{d}p''\ \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'x'}\ p'^2 \delta(p'-p'')\ \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}p''x''} + V(x') \langle x' | x'' \rangle \ \ \ = \frac{1}{2m} \frac{1}{2\pi\hbar} \int \mathrm{d}p'\ p'^2\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'(x'-x'')} + V(x') \delta(x'-x'') \ \ \ = \frac{1}{2m} \frac{1}{2\pi\hbar} \int \mathrm{d}p' \left(-\hbar^2 \frac{\partial^2}{\partial^2 x'} \right) \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'(x'-x'')} + V(x') \delta(x'-x'') \ \ \ = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial^2 x'} \frac{1}{2\pi\hbar} \int \mathrm{d}p'\ \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p'(x'-x'')} + V(x') \delta(x'-x'') \ \ \ = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x'^2} \delta(x'-x'') + V(x') \delta(x'-x'') ( H ) x ′ x ′′ = ⟨ x ′ ∣ H ^ ∣ x ′′ ⟩ = 2 m 1 ⟨ x ′ ∣ p ^ 2 ∣ x ′′ ⟩ + ⟨ x ′ ∣ V ^ ∣ x ′′ ⟩ = 2 m 1 ∫∫ d p ′ d p ′′ ⟨ x ′ ∣ p ′ ⟩ ⟨ p ′ ∣ p ^ 2 ∣ p ′′ ⟩ ⟨ p ′′ ∣ x ′′ ⟩ + ⟨ x ′ ∣ V ( x ) ∣ x ′′ ⟩ = 2 m 1 ∫∫ d p ′ d p ′′ 2 π ℏ 1 e ℏ i p ′ x ′ p ′2 δ ( p ′ − p ′′ ) 2 π ℏ 1 e − ℏ i p ′′ x ′′ + V ( x ′ ) ⟨ x ′ ∣ x ′′ ⟩ = 2 m 1 2 π ℏ 1 ∫ d p ′ p ′2 e ℏ i p ′ ( x ′ − x ′′ ) + V ( x ′ ) δ ( x ′ − x ′′ ) = 2 m 1 2 π ℏ 1 ∫ d p ′ ( − ℏ 2 ∂ 2 x ′ ∂ 2 ) e ℏ i p ′ ( x ′ − x ′′ ) + V ( x ′ ) δ ( x ′ − x ′′ ) = − 2 m ℏ 2 ∂ 2 x ′ ∂ 2 2 π ℏ 1 ∫ d p ′ e ℏ i p ′ ( x ′ − x ′′ ) + V ( x ′ ) δ ( x ′ − x ′′ ) = − 2 m ℏ 2 ∂ x ′2 ∂ 2 δ ( x ′ − x ′′ ) + V ( x ′ ) δ ( x ′ − x ′′ )
坐标 x ^ \hat{x} x ^
( x ) p ′ p ′ ′ = ⟨ p ′ ∣ x ^ ∣ p ′ ′ ⟩ = ∫ ∫ d x ′ d x ′ ′ ⟨ p ′ ∣ x ′ ⟩ ⟨ x ′ ∣ x ^ ∣ x ′ ′ ⟩ ⟨ x ′ ′ ∣ p ′ ′ ⟩ = ∫ ∫ d x ′ d x ′ ′ 1 2 π ℏ e − i ℏ p ′ x ′ x ′ δ ( x ′ − x ′ ′ ) 1 2 π ℏ e i ℏ p ′ ′ x ′ ′ = 1 2 π ℏ ∫ d x ′ x ′ e − i ℏ ( p ′ − p ′ ′ ) x ′ = 1 2 π ℏ ∫ d x ′ ( i ℏ ∂ ∂ p ′ ) e − i ℏ ( p ′ − p ′ ′ ) x ′ = i ℏ ∂ ∂ p ′ 1 2 π ℏ ∫ d x ′ e − i ℏ ( p ′ − p ′ ′ ) x ′ = i ℏ ∂ ∂ p ′ δ ( p ′ − p ′ ′ ) (x)_{p'p''} = \langle p' | \hat{x} | p'' \rangle = \int \int \mathrm{d}x'\ \mathrm{d}x''\ \langle p' | x' \rangle\ \langle x' | \hat{x} | x'' \rangle\ \langle x'' | p'' \rangle \ \ \ = \int \int \mathrm{d}x'\ \mathrm{d}x''\ \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}p'x'}\ x' \delta(x'-x'')\ \frac{1}{\sqrt{2\pi\hbar}} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}p''x''} \ \ \ = \frac{1}{2\pi\hbar} \int \mathrm{d}x'\ x'\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}(p'-p'')x'} \ \ \ = \frac{1}{2\pi\hbar} \int \mathrm{d}x' \left(\mathrm{i}\hbar \frac{\partial}{\partial p'} \right) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}(p'-p'')x'} \ \ \ = \mathrm{i}\hbar \frac{\partial}{\partial p'} \frac{1}{2\pi\hbar} \int \mathrm{d}x'\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}(p'-p'')x'} \ \ \ = \mathrm{i}\hbar \frac{\partial}{\partial p'} \delta(p'-p'') ( x ) p ′ p ′′ = ⟨ p ′ ∣ x ^ ∣ p ′′ ⟩ = ∫∫ d x ′ d x ′′ ⟨ p ′ ∣ x ′ ⟩ ⟨ x ′ ∣ x ^ ∣ x ′′ ⟩ ⟨ x ′′ ∣ p ′′ ⟩ = ∫∫ d x ′ d x ′′ 2 π ℏ 1 e − ℏ i p ′ x ′ x ′ δ ( x ′ − x ′′ ) 2 π ℏ 1 e ℏ i p ′′ x ′′ = 2 π ℏ 1 ∫ d x ′ x ′ e − ℏ i ( p ′ − p ′′ ) x ′ = 2 π ℏ 1 ∫ d x ′ ( i ℏ ∂ p ′ ∂ ) e − ℏ i ( p ′ − p ′′ ) x ′ = i ℏ ∂ p ′ ∂ 2 π ℏ 1 ∫ d x ′ e − ℏ i ( p ′ − p ′′ ) x ′ = i ℏ ∂ p ′ ∂ δ ( p ′ − p ′′ )
动量 p ^ \hat{p} p ^
( p ) p ′ p ′ ′ = ⟨ p ′ ∣ p ^ ∣ p ′ ′ ⟩ = [ ⟨ p ′ ∣ p ^ ] p ′ ′ ⟩ = p ′ ⟨ p ′ ∣ p ′ ′ ⟩ = p ′ δ ( p ′ − p ′ ′ ) (p)_{p'p''} = \langle p' | \hat{p} | p'' \rangle = \left[ \langle p' | \hat{p} \right] p'' \rangle = p' \langle p' | p'' \rangle = p' \delta(p'-p'') ( p ) p ′ p ′′ = ⟨ p ′ ∣ p ^ ∣ p ′′ ⟩ = [ ⟨ p ′ ∣ p ^ ] p ′′ ⟩ = p ′ ⟨ p ′ ∣ p ′′ ⟩ = p ′ δ ( p ′ − p ′′ )
哈密顿量 H ^ \hat{H} H ^
( H ) p ′ p ′ ′ = ⟨ p ′ ∣ H ^ ∣ p ′ ′ ⟩ = 1 2 m ⟨ p ′ ∣ p ^ 2 ∣ p ′ ′ ⟩ + ⟨ p ′ ∣ V ^ ∣ p ′ ′ ⟩ = p ′ 2 2 m δ ( p ′ − p ′ ′ ) + ⟨ p ′ ∣ V ( i ℏ ∂ ∂ p ) ∣ p ′ ′ ⟩ = p ′ 2 2 m δ ( p ′ − p ′ ′ ) + V ( i ℏ ∂ ∂ p ′ ) ⟨ p ′ ∣ p ′ ′ ⟩ = p ′ 2 2 m δ ( p ′ − p ′ ′ ) + V ( i ℏ ∂ ∂ p ′ ) δ ( p ′ − p ′ ′ ) (H)_{p'p''} = \langle p' | \hat{H} | p'' \rangle = \frac{1}{2m} \langle p' | \hat{p}^2 | p'' \rangle + \langle p' | \hat{V} | p'' \rangle \ \ \ = \frac{p'^2}{2m} \delta(p'-p'') + \langle p' | V\left( \mathrm{i}\hbar{\frac{\partial}{\partial p}} \right) | p'' \rangle \ \ \ = \frac{p'^2}{2m} \delta(p'-p'') + V\left( \mathrm{i}\hbar{\frac{\partial}{\partial p'}} \right) \langle p' | p'' \rangle \ \ \ = \frac{p'^2}{2m} \delta(p'-p'') + V\left( \mathrm{i}\hbar{\frac{\partial}{\partial p'}} \right) \delta(p'-p'') ( H ) p ′ p ′′ = ⟨ p ′ ∣ H ^ ∣ p ′′ ⟩ = 2 m 1 ⟨ p ′ ∣ p ^ 2 ∣ p ′′ ⟩ + ⟨ p ′ ∣ V ^ ∣ p ′′ ⟩ = 2 m p ′2 δ ( p ′ − p ′′ ) + ⟨ p ′ ∣ V ( i ℏ ∂ p ∂ ) ∣ p ′′ ⟩ = 2 m p ′2 δ ( p ′ − p ′′ ) + V ( i ℏ ∂ p ′ ∂ ) ⟨ p ′ ∣ p ′′ ⟩ = 2 m p ′2 δ ( p ′ − p ′′ ) + V ( i ℏ ∂ p ′ ∂ ) δ ( p ′ − p ′′ )
势场 V V V
i ℏ ∂ ∂ t ∣ ψ ( t ) ⟩ = H ^ ∣ ψ ( t ) ⟩ = ( T + V ) ∣ ψ ( t ) ⟩ \mathrm{i}\hbar \frac{\partial}{\partial t} | \psi(t) \rangle = \hat{H} | \psi(t) \rangle = (T+V) | \psi(t) \rangle i ℏ ∂ t ∂ ∣ ψ ( t )⟩ = H ^ ∣ ψ ( t )⟩ = ( T + V ) ∣ ψ ( t )⟩
用 ⟨ x ∣ \langle x | ⟨ x ∣
i ℏ ∂ ∂ t ⟨ x ∣ ψ ( t ) ⟩ = ⟨ x ∣ H ^ ∣ ψ ( t ) ⟩ \mathrm{i}\hbar \frac{\partial}{\partial t} \langle x | \psi(t) \rangle = \langle x | \hat{H} | \psi(t) \rangle i ℏ ∂ t ∂ ⟨ x ∣ ψ ( t )⟩ = ⟨ x ∣ H ^ ∣ ψ ( t )⟩
根据 ⟨ x ∣ ψ ( t ) ⟩ = ψ ( x , t ) \langle x| \psi(t) \rangle = \psi(x,t) ⟨ x ∣ ψ ( t )⟩ = ψ ( x , t )
i ℏ ∂ ∂ t ψ ( x , t ) = ∫ d x ′ ⟨ x ∣ H ^ ∣ x ′ ⟩ ⟨ x ′ ∣ ψ ( t ) ⟩ = ∫ d x ′ [ − ℏ 2 2 m ∂ 2 ∂ 2 x δ ( x − x ′ ) + V ( x ) δ ( x − x ′ ) ] ψ ( x ′ , t ) = [ − ℏ 2 2 m ∂ 2 ∂ x 2 + V ( x ) ] ψ ( x , t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(x,t) = \int \mathrm{d}x'\ \langle x | \hat{H} | x' \rangle\ \langle x' | \psi(t) \rangle \ \ \ = \int \mathrm{d}x'\ \left[ -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial^2 x} \delta(x-x') + V(x) \delta(x-x') \right] \psi(x',t) \ \ \ = \left[ -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + V(x) \right] \psi(x,t) i ℏ ∂ t ∂ ψ ( x , t ) = ∫ d x ′ ⟨ x ∣ H ^ ∣ x ′ ⟩ ⟨ x ′ ∣ ψ ( t )⟩ = ∫ d x ′ [ − 2 m ℏ 2 ∂ 2 x ∂ 2 δ ( x − x ′ ) + V ( x ) δ ( x − x ′ ) ] ψ ( x ′ , t ) = [ − 2 m ℏ 2 ∂ x 2 ∂ 2 + V ( x ) ] ψ ( x , t )
用 ⟨ p ∣ \langle p | ⟨ p ∣
i ℏ ∂ ∂ t ⟨ p ∣ ψ ( t ) ⟩ = ⟨ p ∣ H ^ ∣ ψ ( t ) ⟩ \mathrm{i}\hbar \frac{\partial}{\partial t} \langle p | \psi(t) \rangle = \langle p | \hat{H} | \psi(t) \rangle i ℏ ∂ t ∂ ⟨ p ∣ ψ ( t )⟩ = ⟨ p ∣ H ^ ∣ ψ ( t )⟩
根据 ⟨ p ∣ ψ ( t ) ⟩ = ψ ( p , t ) \langle p | \psi(t) \rangle = \psi(p,t) ⟨ p ∣ ψ ( t )⟩ = ψ ( p , t )
i ℏ ∂ ∂ t ψ ( p , t ) = ∫ d p ′ ⟨ p ∣ H ^ ∣ p ′ ⟩ ⟨ p ′ ∣ ψ ( t ) ⟩ = ∫ d p ′ [ p 2 2 m δ ( p − p ′ ) + V ( i ℏ ∂ ∂ p ) δ ( p − p ′ ) ] ψ ( p ′ , t ) = [ p 2 2 m + V ( i ℏ ∂ ∂ p ) ] ψ ( p , t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(p,t) = \int \mathrm{d}p'\ \langle p | \hat{H} | p' \rangle\ \langle p' | \psi(t) \rangle \ \ \ = \int \mathrm{d}p'\ \left[ \frac{p^2}{2m} \delta(p-p') + V\left( \mathrm{i}\hbar{\frac{\partial}{\partial p}} \right) \delta(p-p') \right] \psi(p',t) \ \ \ = \left[ \frac{p^2}{2m} + V\left( \mathrm{i}\hbar{\frac{\partial}{\partial p}} \right) \right] \psi(p,t) i ℏ ∂ t ∂ ψ ( p , t ) = ∫ d p ′ ⟨ p ∣ H ^ ∣ p ′ ⟩ ⟨ p ′ ∣ ψ ( t )⟩ = ∫ d p ′ [ 2 m p 2 δ ( p − p ′ ) + V ( i ℏ ∂ p ∂ ) δ ( p − p ′ ) ] ψ ( p ′ , t ) = [ 2 m p 2 + V ( i ℏ ∂ p ∂ ) ] ψ ( p , t )
动能 T = p 2 2 m T = \frac{p^2}{2m} T = 2 m p 2
T ˉ = ⟨ ψ ∣ T ∣ ψ ⟩ = ⟨ ψ ∣ p 2 2 m ∣ ψ ⟩ = 1 2 m ∫ ∫ d x d x ′ ⟨ ψ ∣ x ⟩ ⟨ x ∣ p 2 ∣ x ′ ⟩ ⟨ x ′ ∣ ψ ⟩ = 1 2 m ∫ ∫ d x d x ′ ψ ∗ ( x ) [ − ℏ 2 ∂ 2 ∂ 2 x δ ( x − x ′ ) ] ψ ( x ′ ) = 1 2 m ∫ d x ψ ∗ ( x ) ( − ℏ 2 ∂ 2 ∂ x 2 ) ψ ( x ) \bar{T} = \langle \psi | T | \psi \rangle = \langle \psi | \frac{p^2}{2m}| \psi \rangle \ \ \ = \frac{1}{2m} \int \int \mathrm{d}x\ \mathrm{d}x'\ \langle \psi | x \rangle\ \langle x | p^2 | x' \rangle\ \langle x' | \psi \rangle \ \ \ = \frac{1}{2m} \int \int \mathrm{d}x\ \mathrm{d}x'\ \psi^(x) \left[ -\hbar^2 \frac{\partial^2}{\partial^2 x} \delta(x-x') \right] \psi(x') \ \ \ = \frac{1}{2m} \int \mathrm{d}x\ \psi^ (x) \left( -\hbar^2 \frac{\partial^2}{\partial x^2} \right) \psi(x) T ˉ = ⟨ ψ ∣ T ∣ ψ ⟩ = ⟨ ψ ∣ 2 m p 2 ∣ ψ ⟩ = 2 m 1 ∫∫ d x d x ′ ⟨ ψ ∣ x ⟩ ⟨ x ∣ p 2 ∣ x ′ ⟩ ⟨ x ′ ∣ ψ ⟩ = 2 m 1 ∫∫ d x d x ′ ψ ∗ ( x ) [ − ℏ 2 ∂ 2 x ∂ 2 δ ( x − x ′ ) ] ψ ( x ′ ) = 2 m 1 ∫ d x ψ ∗ ( x ) ( − ℏ 2 ∂ x 2 ∂ 2 ) ψ ( x )
势能 V ( x ) V(x) V ( x )
V ˉ = ⟨ ψ ∣ V ( x ) ∣ ψ ⟩ = ∫ ∫ d x d x ′ ⟨ ψ ∣ x ⟩ ⟨ x ∣ V ( x ) ∣ x ′ ⟩ ⟨ x ′ ∣ ψ ⟩ = ∫ ∫ d x d x ′ ψ ∗ ( x ) V ( x ) δ ( x − x ′ ) ψ ( x ′ ) = ∫ d x ψ ∗ ( x ) V ( x ) ψ ( x ) \bar{V} = \langle \psi | V(x) | \psi \rangle \ \ \ = \int \int \mathrm{d}x\ \mathrm{d}x'\ \langle \psi | x \rangle\ \langle x | V(x) | x' \rangle\ \langle x ' | \psi \rangle \ \ \ = \int \int \mathrm{d}x\ \mathrm{d}x'\ \psi^(x)\ V(x) \delta(x-x')\ \psi(x') \ \ \ = \int \mathrm{d}x\ \psi^ (x) V(x) \psi(x) V ˉ = ⟨ ψ ∣ V ( x ) ∣ ψ ⟩ = ∫∫ d x d x ′ ⟨ ψ ∣ x ⟩ ⟨ x ∣ V ( x ) ∣ x ′ ⟩ ⟨ x ′ ∣ ψ ⟩ = ∫∫ d x d x ′ ψ ∗ ( x ) V ( x ) δ ( x − x ′ ) ψ ( x ′ ) = ∫ d x ψ ∗ ( x ) V ( x ) ψ ( x )
动能 T = p 2 2 m T = \frac{p^2}{2m} T = 2 m p 2
T ˉ = ⟨ ψ ∣ T ∣ ψ ⟩ = ⟨ ψ ∣ p 2 2 m ∣ ψ ⟩ = 1 2 m ∫ ∫ d p d p ′ ⟨ ψ ∣ p ⟩ ⟨ p ∣ p 2 ∣ p ′ ⟩ ⟨ p ′ ∣ ψ ⟩ = 1 2 m ∫ ∫ d p d p ′ ψ ∗ ( p ) p 2 δ ( p − p ′ ) ψ ( p ′ ) = 1 2 m ∫ d p ψ ∗ ( p ) p 2 ψ ( p ) \bar{T} = \langle \psi | T | \psi \rangle = \langle \psi | \frac{p^2}{2m}| \psi \rangle \ \ \ = \frac{1}{2m} \int \int \mathrm{d}p\ \mathrm{d}p'\ \langle \psi | p \rangle\ \langle p | p^2 | p' \rangle\ \langle p' | \psi \rangle \ \ \ = \frac{1}{2m} \int \int \mathrm{d}p\ \mathrm{d}p'\ \psi^(p)\ p^2 \delta(p-p')\ \psi(p') \ \ \ = \frac{1}{2m} \int \mathrm{d}p\ \psi^ (p) p^2 \psi(p) T ˉ = ⟨ ψ ∣ T ∣ ψ ⟩ = ⟨ ψ ∣ 2 m p 2 ∣ ψ ⟩ = 2 m 1 ∫∫ d p d p ′ ⟨ ψ ∣ p ⟩ ⟨ p ∣ p 2 ∣ p ′ ⟩ ⟨ p ′ ∣ ψ ⟩ = 2 m 1 ∫∫ d p d p ′ ψ ∗ ( p ) p 2 δ ( p − p ′ ) ψ ( p ′ ) = 2 m 1 ∫ d p ψ ∗ ( p ) p 2 ψ ( p )
势能 V ( x ) V(x) V ( x )
V ˉ = ⟨ ψ ∣ V ( i ℏ ∂ ∂ p ) ∣ ψ ⟩ = ∫ ∫ d p d p ′ ⟨ ψ ∣ p ⟩ ⟨ p ∣ V ( i ℏ ∂ ∂ p ) ∣ p ′ ⟩ ⟨ p ′ ∣ ψ ⟩ = ∫ ∫ d p d p ′ ψ ∗ ( p ) V ( i ℏ ∂ ∂ p ) δ ( p − p ′ ) ψ ( p ′ ) = ∫ d p ψ ∗ ( p ) V ( i ℏ ∂ ∂ p ) ψ ( p ) \bar{V} = \langle \psi | V \left (\mathrm{i}\hbar\frac{\partial}{\partial p} \right) | \psi \rangle \ \ \ = \int \int \mathrm{d}p\ \mathrm{d}p'\ \langle \psi | p \rangle\ \langle p | V \left (\mathrm{i}\hbar\frac{\partial}{\partial p} \right) | p' \rangle\ \langle p' | \psi \rangle \ \ \ = \int \int \mathrm{d}p\ \mathrm{d}p'\ \psi^(p)\ V \left (\mathrm{i}\hbar\frac{\partial}{\partial p} \right) \delta(p-p')\ \psi(p') \ \ \ = \int \mathrm{d}p\ \psi^ (p) V \left (\mathrm{i}\hbar\frac{\partial}{\partial p} \right) \psi(p) V ˉ = ⟨ ψ ∣ V ( i ℏ ∂ p ∂ ) ∣ ψ ⟩ = ∫∫ d p d p ′ ⟨ ψ ∣ p ⟩ ⟨ p ∣ V ( i ℏ ∂ p ∂ ) ∣ p ′ ⟩ ⟨ p ′ ∣ ψ ⟩ = ∫∫ d p d p ′ ψ ∗ ( p ) V ( i ℏ ∂ p ∂ ) δ ( p − p ′ ) ψ ( p ′ ) = ∫ d p ψ ∗ ( p ) V ( i ℏ ∂ p ∂ ) ψ ( p )
一维谐振子的哈密顿量
H ^ = 1 2 m p ^ 2 + 1 2 m ω 2 x ^ 2 \hat{H} = \frac{1}{2m} \hat{p}^2 + \frac{1}{2} m \omega^2 \hat{x}^2 H ^ = 2 m 1 p ^ 2 + 2 1 m ω 2 x ^ 2
引入一对互为厄米共轭的算符
a ^ = m ω 2 ℏ ( x ^ + i m ω p ^ ) a ^ + = m ω 2 ℏ ( x ^ − i m ω p ^ ) \hat{a} = \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} + \frac{\mathrm{i}}{m\omega} \hat{p} \right) \ \ \ \hat{a}^+ = \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} - \frac{\mathrm{i}}{m\omega} \hat{p} \right) a ^ = 2ℏ mω ( x ^ + mω i p ^ ) a ^ + = 2ℏ mω ( x ^ − mω i p ^ )
注意这两个算符不是厄米算符。
这两个算符的对易关系为
[ a ^ , a ^ + ] = m ω 2 ℏ [ x ^ + i m ω p ^ , x ^ − i m ω p ^ ] = m ω 2 ℏ { [ x ^ , x ^ ] − i m ω [ x ^ , p ^ ] + i m ω [ p ^ , x ^ ] + 1 m 2 ω 2 [ p ^ , p ^ ] } = m ω 2 ℏ ( − i m ω i ℏ − i m ω i ℏ ) = 1 [ \hat{a} , \hat{a}^+ ] = \frac{m\omega}{2\hbar} \left[ \hat{x} + \frac{\mathrm{i}}{m\omega} \hat{p} , \hat{x} - \frac{\mathrm{i}}{m\omega} \hat{p} \right] \ \ \ = \frac{m\omega}{2\hbar} \left{ [\hat{x} , \hat{x}] - \frac{\mathrm{i}}{m\omega} [\hat{x} , \hat{p}] + \frac{\mathrm{i}}{m\omega} [\hat{p} , \hat{x}] + \frac{1}{m^2\omega^2} [\hat{p} , \hat{p}] \right} \ \ \ = \frac{m\omega}{2\hbar} \left( -\frac{\mathrm{i}}{m\omega} \mathrm{i\hbar} - \frac{\mathrm{i}}{m\omega} \mathrm{i\hbar}\right) \ \ \ = 1 [ a ^ , a ^ + ] = 2ℏ mω [ x ^ + mω i p ^ , x ^ − mω i p ^ ] = 2ℏ mω { [ x ^ , x ^ ] − mω i [ x ^ , p ^ ] + mω i [ p ^ , x ^ ] + m 2 ω 2 1 [ p ^ , p ^ ] } = 2ℏ mω ( − mω i iℏ − mω i iℏ ) = 1
使用 a ^ \hat{a} a ^ a ^ + \hat{a}^+ a ^ +
x ^ = ℏ 2 m ω ( a ^ + + a ^ ) p ^ = i ℏ m ω 2 ( a ^ + − a ^ ) \hat{x} = \sqrt{\frac{\hbar}{2m\omega}} (\hat{a}^+ + \hat{a}) \ \ \ \hat{p} = \mathrm{i} \sqrt{\frac{\hbar m\omega}{2}} (\hat{a}^+ - \hat{a}) x ^ = 2 mω ℏ ( a ^ + + a ^ ) p ^ = i 2 ℏ mω ( a ^ + − a ^ )
则哈密顿量也可以用 a ^ \hat{a} a ^ a ^ + \hat{a}^+ a ^ +
H ^ = 1 2 m p ^ 2 + 1 2 m ω 2 x ^ 2 = 1 2 m [ i ℏ m ω 2 ( a ^ + − a ^ ) ] 2 + 1 2 m ω 2 [ ℏ 2 m ω ( a ^ + + a ^ ) ] 2 = − ℏ ω 4 [ ( a ^ + ) 2 − a ^ + a ^ − a ^ a ^ + + a ^ 2 ] + ℏ ω 4 [ ( a ^ + ) 2 + a ^ + a ^ + a ^ a ^ + + a ^ 2 ] = ℏ ω 2 ( a ^ + a ^ + a ^ a ^ + ) = ℏ ω 2 [ a ^ + a ^ + ( a ^ + a ^ + 1 ) ] = ℏ ω ( a ^ + a ^ + 1 2 ) \hat{H} = \frac{1}{2m} \hat{p}^2 + \frac{1}{2} m \omega^2 \hat{x}^2 \ \ \ = \frac{1}{2m} \left[ \mathrm{i} \sqrt{\frac{\hbar m\omega}{2}} (\hat{a}^+ - \hat{a}) \right]^2 + \frac{1}{2} m \omega^2 \left[ \sqrt{\frac{\hbar}{2m\omega}} (\hat{a}^+ + \hat{a})\right]^2 \ \ \ = -\frac{\hbar\omega}{4} [ (\hat{a}^+)^2 - \hat{a}^+\hat{a} - \hat{a}\hat{a}^+ + \hat{a}^2 ] + \frac{\hbar\omega}{4} [ (\hat{a}^+)^2 + \hat{a}^+\hat{a} + \hat{a}\hat{a}^+ + \hat{a}^2 ] \ \ \ = \frac{\hbar\omega}{2} ( \hat{a}^+\hat{a} + \hat{a}\hat{a}^+ ) \ \ \ = \frac{\hbar\omega}{2} [ \hat{a}^+\hat{a} + (\hat{a}^+\hat{a} + 1) ] \ \ \ = \hbar\omega \left( \hat{a}^+\hat{a} + \frac{1}{2} \right) H ^ = 2 m 1 p ^ 2 + 2 1 m ω 2 x ^ 2 = 2 m 1 [ i 2 ℏ mω ( a ^ + − a ^ ) ] 2 + 2 1 m ω 2 [ 2 mω ℏ ( a ^ + + a ^ ) ] 2 = − 4 ℏ ω [( a ^ + ) 2 − a ^ + a ^ − a ^ a ^ + + a ^ 2 ] + 4 ℏ ω [( a ^ + ) 2 + a ^ + a ^ + a ^ a ^ + + a ^ 2 ] = 2 ℏ ω ( a ^ + a ^ + a ^ a ^ + ) = 2 ℏ ω [ a ^ + a ^ + ( a ^ + a ^ + 1 )] = ℏ ω ( a ^ + a ^ + 2 1 )
记 N ^ = a ^ + a ^ \hat{N} = \hat{a}^+\hat{a} N ^ = a ^ + a ^
H ^ = ℏ ω ( N ^ + 1 2 ) \hat{H} = \hbar\omega \left( \hat{N} + \frac{1}{2} \right) H ^ = ℏ ω ( N ^ + 2 1 )
易知 H ^ \hat{H} H ^ N ^ \hat{N} N ^ H ^ \hat{H} H ^ N ^ \hat{N} N ^ N ^ \hat{N} N ^
N ^ ∣ n ⟩ = n ∣ n ⟩ \hat{N} | n \rangle = n | n \rangle N ^ ∣ n ⟩ = n ∣ n ⟩
这里的 n n n
其中本征态 ∣ n ⟩ | n \rangle ∣ n ⟩ ⟨ n ′ ∣ n ⟩ = δ n n ′ \langle n' | n \rangle = \delta_{nn'} ⟨ n ′ ∣ n ⟩ = δ n n ′ ∣ ψ ⟩ | \psi \rangle ∣ ψ ⟩
N ˉ = ⟨ ψ ∣ a ^ + a ^ ∣ ψ ⟩ = ⟨ a ^ ψ ∣ a ^ ψ ⟩ ≥ 0 \bar{N} = \langle \psi | \hat{a}^+\hat{a} | \psi \rangle = \langle \hat{a}\psi | \hat{a}\psi \rangle \ge 0 N ˉ = ⟨ ψ ∣ a ^ + a ^ ∣ ψ ⟩ = ⟨ a ^ ψ ∣ a ^ ψ ⟩ ≥ 0
由此可得 N ^ \hat{N} N ^ N ^ \hat{N} N ^ a ^ + , a ^ \hat{a}^+,\hat{a} a ^ + , a ^
[ N ^ , a ^ + ] = [ a ^ + a ^ , a ^ + ] = a ^ + [ a ^ , a ^ + ] + [ a ^ + , a ^ + ] a ^ = a ^ + [ N ^ , a ^ ] = [ a ^ + a ^ , a ^ ] = a ^ + [ a ^ , a ^ ] + [ a ^ + , a ^ ] a ^ = − a ^ [ \hat{N} , \hat{a}^+ ] = [ \hat{a}^+ \hat{a} , \hat{a}^+ ] = \hat{a}^+ [ \hat{a} , \hat{a}^+ ] + [ \hat{a}^+ , \hat{a}^+ ] \hat{a} = \hat{a}^+ \ \ \ \ [ \hat{N} , \hat{a} ] = [ \hat{a}^+ \hat{a} , \hat{a} ] = \hat{a}^+ [ \hat{a} , \hat{a} ] + [ \hat{a}^+ , \hat{a} ] \hat{a} = - \hat{a} [ N ^ , a ^ + ] = [ a ^ + a ^ , a ^ + ] = a ^ + [ a ^ , a ^ + ] + [ a ^ + , a ^ + ] a ^ = a ^ + [ N ^ , a ^ ] = [ a ^ + a ^ , a ^ ] = a ^ + [ a ^ , a ^ ] + [ a ^ + , a ^ ] a ^ = − a ^
则
N ^ a ^ ∣ n ⟩ = ( a ^ N ^ − a ^ ) ∣ n ⟩ = a ^ N ^ ∣ n ⟩ − a ^ ∣ n ⟩ = a ^ n ∣ n ⟩ − a ^ ∣ n ⟩ = ( n − 1 ) a ^ ∣ n ⟩ \hat{N} \hat{a} | n \rangle = (\hat{a}\hat{N}-\hat{a}) | n \rangle = \hat{a}\hat{N} | n \rangle - \hat{a} | n \rangle = \hat{a}n | n \rangle - \hat{a} | n \rangle = (n-1) \hat{a} | n \rangle N ^ a ^ ∣ n ⟩ = ( a ^ N ^ − a ^ ) ∣ n ⟩ = a ^ N ^ ∣ n ⟩ − a ^ ∣ n ⟩ = a ^ n ∣ n ⟩ − a ^ ∣ n ⟩ = ( n − 1 ) a ^ ∣ n ⟩
故 a ^ ∣ n ⟩ \hat{a} | n \rangle a ^ ∣ n ⟩ N ^ \hat{N} N ^ ( n − 1 ) (n-1) ( n − 1 ) N ^ ∣ n − 1 ⟩ = ( n − 1 ) ∣ n − 1 ⟩ \hat{N} | n-1 \rangle = (n-1) | n-1 \rangle N ^ ∣ n − 1 ⟩ = ( n − 1 ) ∣ n − 1 ⟩ N N N a ^ ∣ n ⟩ \hat{a} | n \rangle a ^ ∣ n ⟩ n − 1 ⟩ \ n-1 \rangle n − 1 ⟩
a ^ ∣ n ⟩ = λ n ∣ n − 1 ⟩ \hat{a} | n \rangle = \lambda_n | n-1 \rangle a ^ ∣ n ⟩ = λ n ∣ n − 1 ⟩
故
n = ⟨ n ∣ N ^ ∣ n ⟩ = ⟨ n ∣ a ^ + a ^ ∣ n ⟩ = ∣ λ n ∣ 2 ⟨ n − 1 ∣ n − 1 ⟩ = ∣ λ n ∣ 2 n = \langle n | \hat{N} | n \rangle = \langle n | \hat{a}^+\hat{a} | n \rangle \ \ \ = | \lambda_n |^2 \langle n-1 | n-1 \rangle = | \lambda_n |^2 n = ⟨ n ∣ N ^ ∣ n ⟩ = ⟨ n ∣ a ^ + a ^ ∣ n ⟩ = ∣ λ n ∣ 2 ⟨ n − 1∣ n − 1 ⟩ = ∣ λ n ∣ 2
取 λ n = n \lambda_n = \sqrt{n} λ n = n
a ^ ∣ n ⟩ = n ∣ n − 1 ⟩ \hat{a} | n \rangle = \sqrt{n} | n-1 \rangle a ^ ∣ n ⟩ = n ∣ n − 1 ⟩
同理,
N ^ a ^ + ∣ n ⟩ = ( a ^ + N ^ + a ^ + ) ∣ n ⟩ = ( n + 1 ) a ^ + ∣ n ⟩ \hat{N} \hat{a}^+ | n \rangle = (\hat{a}^+\hat{N} + \hat{a}^+) | n \rangle = (n+1) \hat{a}^+ | n \rangle N ^ a ^ + ∣ n ⟩ = ( a ^ + N ^ + a ^ + ) ∣ n ⟩ = ( n + 1 ) a ^ + ∣ n ⟩
故 a ^ + ∣ n ⟩ \hat{a}^+ | n \rangle a ^ + ∣ n ⟩ N ^ \hat{N} N ^ ( n + 1 ) (n+1) ( n + 1 ) N ^ ∣ n = 1 ⟩ = ( n + 1 ) ∣ n + 1 ⟩ \hat{N} | n=1 \rangle = (n+1) | n+1 \rangle N ^ ∣ n = 1 ⟩ = ( n + 1 ) ∣ n + 1 ⟩ N N N a ^ + ∣ n ⟩ \hat{a}^+ | n \rangle a ^ + ∣ n ⟩ n + 1 ⟩ \ n+1 \rangle n + 1 ⟩
a ^ + ∣ n ⟩ = μ n ∣ n + 1 ⟩ \hat{a}^+ | n \rangle = \mu_n | n+1 \rangle a ^ + ∣ n ⟩ = μ n ∣ n + 1 ⟩
故
n + 1 = ⟨ n ∣ N ^ + 1 ∣ n ⟩ = ⟨ n ∣ a ^ + a ^ + 1 ∣ n ⟩ = ⟨ n ∣ a ^ a ^ + ∣ n ⟩ = ∣ μ n ∣ 2 ⟨ n + 1 ∣ n + 1 ⟩ = ∣ μ n ∣ 2 n + 1 = \langle n | \hat{N} + 1 | n \rangle = \langle n | \hat{a}^+\hat{a} + 1 | n \rangle \ \ \ = \langle n | \hat{a}\hat{a}^+ | n \rangle = | \mu_n |^2 \langle n+1 | n+1 \rangle = | \mu_n |^2 n + 1 = ⟨ n ∣ N ^ + 1∣ n ⟩ = ⟨ n ∣ a ^ + a ^ + 1∣ n ⟩ = ⟨ n ∣ a ^ a ^ + ∣ n ⟩ = ∣ μ n ∣ 2 ⟨ n + 1∣ n + 1 ⟩ = ∣ μ n ∣ 2
取 μ n = n + 1 \mu_n = \sqrt{n+1} μ n = n + 1
a ^ + ∣ n ⟩ = n + 1 ∣ n + 1 ⟩ \hat{a}^+ | n \rangle = \sqrt{n+1} | n+1 \rangle a ^ + ∣ n ⟩ = n + 1 ∣ n + 1 ⟩
可以发现,通过 a ^ \hat{a} a ^ a ^ + \hat{a}^+ a ^ + ∣ n ⟩ |n\rangle ∣ n ⟩ ∣ n − 1 ⟩ |n-1\rangle ∣ n − 1 ⟩ ∣ n + 1 ⟩ |n+1\rangle ∣ n + 1 ⟩ N ^ \hat{N} N ^ a ^ \hat{a} a ^ N ^ \hat{N} N ^ a ^ + \hat{a}^+ a ^ +
在量子场论中电磁辐射场(二次)量子化后成为光子, a ^ \hat{a} a ^ a ^ + \hat{a}^+ a ^ +
由 N ^ \hat{N} N ^ ∣ n ⟩ |n\rangle ∣ n ⟩ a ^ \hat{a} a ^ N ^ \hat{N} N ^
∣ n ⟩ , a ^ ∣ n ⟩ ∝ ∣ n − 1 ⟩ , a ^ 2 ∣ n ⟩ ∝ ∣ n − 2 ⟩ , ⋯ |n\rangle ,\kern 1em \hat{a}|n\rangle \propto |n-1\rangle ,\kern 1em \hat{a}^2|n\rangle \propto |n-2\rangle , \kern 1em \cdots ∣ n ⟩ , a ^ ∣ n ⟩ ∝ ∣ n − 1 ⟩ , a ^ 2 ∣ n ⟩ ∝ ∣ n − 2 ⟩ , ⋯
考虑到 N ^ \hat{N} N ^ n ≥ 0 n\ge0 n ≥ 0 n 0 n_0 n 0 ∣ n 0 ⟩ |n_0\rangle ∣ n 0 ⟩ a ^ ∣ n 0 ⟩ = n 0 ∣ n 0 − 1 ⟩ \hat{a}|n_0\rangle = \sqrt{n_0}|n_0-1\rangle a ^ ∣ n 0 ⟩ = n 0 ∣ n 0 − 1 ⟩ N ^ \hat{N} N ^ n 0 > 0 n_0>0 n 0 > 0 n 0 − 1 < n 0 n_0-1<n_0 n 0 − 1 < n 0 n 0 n_0 n 0 n 0 = 0 n_0=0 n 0 = 0 a ^ ∣ n 0 ⟩ = n 0 ∣ n 0 − 1 ⟩ = 0 \hat{a}|n_0\rangle = \sqrt{n_0}|n_0-1\rangle = 0 a ^ ∣ n 0 ⟩ = n 0 ∣ n 0 − 1 ⟩ = 0 0 0 0 N ^ \hat{N} N ^ n 0 = 0 n_0=0 n 0 = 0 ∣ 0 ⟩ |0\rangle ∣0 ⟩
从 ∣ 0 ⟩ |0\rangle ∣0 ⟩ a ^ + \hat{a}^+ a ^ + N ^ \hat{N} N ^
∣ 0 ⟩ , a ^ + ∣ 0 ⟩ ∝ ∣ 1 ⟩ , ( a ^ + ) 2 ∣ 0 ⟩ ∝ ∣ 2 ⟩ , ⋯ |0\rangle ,\kern 1em \hat{a}^+|0\rangle \propto |1\rangle ,\kern 1em (\hat{a}^+)^2|0\rangle \propto |2\rangle , \kern 1em \cdots ∣0 ⟩ , a ^ + ∣0 ⟩ ∝ ∣1 ⟩ , ( a ^ + ) 2 ∣0 ⟩ ∝ ∣2 ⟩ , ⋯
用归纳法可以证明 N ^ \hat{N} N ^
∣ n ⟩ = 1 n ! ( a ^ + ) n ∣ 0 ⟩ |n\rangle = \frac{1}{\sqrt{n!}} (\hat{a}^+)^n |0\rangle ∣ n ⟩ = n ! 1 ( a ^ + ) n ∣0 ⟩
回到对 H ^ = ℏ ω ( N ^ + 1 2 ) \hat{H}=\hbar\omega (\hat{N} + \frac12) H ^ = ℏ ω ( N ^ + 2 1 ) N ^ \hat{N} N ^ 0 , 1 , 2 , ⋯ 0,1,2,\cdots 0 , 1 , 2 , ⋯ H ^ \hat{H} H ^ ( n + 1 2 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ ) (n+\frac12)\hbar\omega \kern 1em (n=0,1,2,\cdots) ( n + 2 1 ) ℏ ω ( n = 0 , 1 , 2 , ⋯ )
H ^ ∣ n ⟩ = ( n + 1 2 ) ℏ ω ∣ n ⟩ \hat{H}|n\rangle = (n+\frac12)\hbar\omega |n\rangle H ^ ∣ n ⟩ = ( n + 2 1 ) ℏ ω ∣ n ⟩
首先考虑基态 ∣ 0 ⟩ |0\rangle ∣0 ⟩ a ^ ∣ 0 ⟩ = 0 \hat{a}|0\rangle = 0 a ^ ∣0 ⟩ = 0 a ^ \hat{a} a ^
m ω 2 ℏ ( x ^ + i m ω p ^ ) ψ 0 ( x ) = m ω 2 ℏ ( x + ℏ m ω d d x ) ψ 0 ( x ) = 0 \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} + \frac{\mathrm{i}}{m\omega} \hat{p} \right) \psi_0(x) = \sqrt{\frac{m\omega}{2\hbar}} \left( x + \frac{\hbar}{m\omega} \frac{\mathrm{d}}{\mathrm{d}x} \right) \psi_0(x) = 0 2ℏ mω ( x ^ + mω i p ^ ) ψ 0 ( x ) = 2ℏ mω ( x + mω ℏ d x d ) ψ 0 ( x ) = 0
这是一个一阶线性常微分方程,容易解得归一化的基态波函数为
ψ 0 ( x ) = ( m ω π ℏ ) 1 4 e − m ω 2 ℏ x 2 \psi_0(x) = \left( \frac{m\omega}{\pi\hbar} \right)^{\frac{1}{4}} \mathrm{e}^{-\frac{m\omega}{2\hbar} x^2} ψ 0 ( x ) = ( π ℏ mω ) 4 1 e − 2ℏ mω x 2
记 α = m ω ℏ \alpha=\sqrt{\frac{m\omega}{\hbar}} α = ℏ mω
ψ 0 ( x ) = ( α 2 π ) 1 4 e − α 2 x 2 2 \psi_0(x) = \left( \frac{\alpha^2}{\pi} \right)^{\frac{1}{4}} \mathrm{e}^{-\frac{\alpha^2x^2}{2}} ψ 0 ( x ) = ( π α 2 ) 4 1 e − 2 α 2 x 2
激发态的波函数可借助 a ^ + \hat{a}^+ a ^ +
ψ n ( x ) = ⟨ x ∣ n ⟩ = 1 n ! ⟨ x ∣ ( a ^ + ) n ∣ 0 ⟩ = 1 n ! m ω 2 ℏ ( x ^ − i m ω p ^ ) ψ 0 ( x ) = 1 ( 2 n ) ! ! ( α 2 π ) 1 4 ( α x − 1 α d d x ) n e − α 2 x 2 2 \psi_n(x) = \langle x | n \rangle = \frac{1}{\sqrt{n!}} \langle x | (\hat{a}^+)^n | 0 \rangle \ \ \ = \frac{1}{\sqrt{n!}} \sqrt{\frac{m\omega}{2\hbar}} \left( \hat{x} - \frac{\mathrm{i}}{m\omega} \hat{p} \right) \psi_0(x) \ \ \ = \frac{1}{\sqrt{(2n)!!}} \left( \frac{\alpha^2}{\pi} \right)^{\frac{1}{4}} \left( \alpha x - \frac{1}{\alpha} \frac{\mathrm{d}}{\mathrm{d}x} \right)^n \mathrm{e}^{-\frac{\alpha^2x^2}{2}} ψ n ( x ) = ⟨ x ∣ n ⟩ = n ! 1 ⟨ x ∣ ( a ^ + ) n ∣0 ⟩ = n ! 1 2ℏ mω ( x ^ − mω i p ^ ) ψ 0 ( x ) = ( 2 n )!! 1 ( π α 2 ) 4 1 ( αx − α 1 d x d ) n e − 2 α 2 x 2
Fock空间:由粒子数算符 N ^ \hat{N} N ^
占有数表象:由 { ∣ n ⟩ , n = 0 , 1 , 2 , ⋯ } { |n\rangle ,\kern 0.5em n=0,1,2,\cdots } { ∣ n ⟩ , n = 0 , 1 , 2 , ⋯ }
一维坐标算符 x ^ \hat{x} x ^
x n ′ n ′ ′ = ⟨ n ′ ∣ x ^ ∣ n ′ ′ ⟩ = ⟨ n ′ ∣ ℏ 2 m ω ( a ^ + + a ^ ) ∣ n ′ ′ ⟩ = ℏ 2 m ω [ ⟨ n ′ ∣ a ^ + ∣ n ′ ′ ⟩ + ⟨ n ′ ∣ a ^ ∣ n ′ ′ ⟩ ] = ℏ 2 m ω [ n ′ ′ + 1 ⟨ n ′ ∣ n ′ ′ + 1 ⟩ + n ′ ′ ⟨ n ′ ∣ n ′ ′ − 1 ⟩ ] = ℏ 2 m ω [ n ′ ′ + 1 δ n ′ , n ′ ′ + 1 + n ′ ′ δ n ′ , n ′ ′ − 1 ] x_{n'n''} = \langle n' | \hat{x} | n'' \rangle = \langle n' | \sqrt{\frac{\hbar}{2m\omega}} (\hat{a}^+ + \hat{a}) | n'' \rangle = \sqrt{\frac{\hbar}{2m\omega}} \left[ \langle n' | \hat{a}^+ | n'' \rangle + \langle n' | \hat{a} | n'' \rangle \right] \ \ \ = \sqrt{\frac{\hbar}{2m\omega}} \left[ \sqrt{n''+1} \langle n' | n''+1 \rangle + \sqrt{n''} \langle n' | n''-1 \rangle \right] \ \ \ = \sqrt{\frac{\hbar}{2m\omega}} \left[ \sqrt{n''+1}\ \delta_{n',n''+1} + \sqrt{n''}\ \delta_{n',n''-1} \right] x n ′ n ′′ = ⟨ n ′ ∣ x ^ ∣ n ′′ ⟩ = ⟨ n ′ ∣ 2 mω ℏ ( a ^ + + a ^ ) ∣ n ′′ ⟩ = 2 mω ℏ [ ⟨ n ′ ∣ a ^ + ∣ n ′′ ⟩ + ⟨ n ′ ∣ a ^ ∣ n ′′ ⟩ ] = 2 mω ℏ [ n ′′ + 1 ⟨ n ′ ∣ n ′′ + 1 ⟩ + n ′′ ⟨ n ′ ∣ n ′′ − 1 ⟩ ] = 2 mω ℏ [ n ′′ + 1 δ n ′ , n ′′ + 1 + n ′′ δ n ′ , n ′′ − 1 ]
一维动量算符 p ^ \hat{p} p ^
p n ′ n ′ ′ = ⟨ n ′ ∣ p ^ ∣ n ′ ′ ⟩ = ⟨ n ′ ∣ i ℏ m ω 2 ( a ^ + − a ^ ) ∣ n ′ ′ ⟩ = i ℏ m ω 2 [ ⟨ n ′ ∣ a ^ + ∣ n ′ ′ ⟩ − ⟨ n ′ ∣ a ^ ∣ n ′ ′ ⟩ ] = i ℏ m ω 2 [ n ′ ′ + 1 ⟨ n ′ ∣ n ′ ′ + 1 ⟩ − n ′ ′ ⟨ n ′ ∣ n ′ ′ − 1 ⟩ ] = i ℏ m ω 2 [ n ′ ′ + 1 δ n ′ , n ′ ′ + 1 − n ′ ′ δ n ′ , n ′ ′ − 1 ] p_{n'n''} = \langle n' | \hat{p} | n'' \rangle = \langle n' | \mathrm{i} \sqrt{\frac{\hbar m\omega}{2}} (\hat{a}^+ - \hat{a}) | n'' \rangle = \mathrm{i} \sqrt{\frac{\hbar m\omega}{2}} \left[ \langle n' | \hat{a}^+ | n'' \rangle - \langle n' | \hat{a} | n'' \rangle \right] \ \ \ = \mathrm{i} \sqrt{\frac{\hbar m\omega}{2}} \left[ \sqrt{n''+1} \langle n' | n''+1 \rangle - \sqrt{n''} \langle n' | n''-1 \rangle \right] \ \ \ = \mathrm{i} \sqrt{\frac{\hbar m\omega}{2}} \left[ \sqrt{n''+1}\ \delta_{n',n''+1} - \sqrt{n''}\ \delta_{n',n''-1} \right] p n ′ n ′′ = ⟨ n ′ ∣ p ^ ∣ n ′′ ⟩ = ⟨ n ′ ∣ i 2 ℏ mω ( a ^ + − a ^ ) ∣ n ′′ ⟩ = i 2 ℏ mω [ ⟨ n ′ ∣ a ^ + ∣ n ′′ ⟩ − ⟨ n ′ ∣ a ^ ∣ n ′′ ⟩ ] = i 2 ℏ mω [ n ′′ + 1 ⟨ n ′ ∣ n ′′ + 1 ⟩ − n ′′ ⟨ n ′ ∣ n ′′ − 1 ⟩ ] = i 2 ℏ mω [ n ′′ + 1 δ n ′ , n ′′ + 1 − n ′′ δ n ′ , n ′′ − 1 ]
对于任意已归一化的波函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) A A A A ˉ = ( ψ , A ^ ψ ) \bar{A} = (\psi , \hat{A}\psi) A ˉ = ( ψ , A ^ ψ ) H ^ ψ = i ℏ ∂ ∂ t ψ \hat{H} \psi = \mathrm{i}\hbar \frac{\partial}{\partial t} \psi H ^ ψ = i ℏ ∂ t ∂ ψ
d d t A ˉ ( t ) = ( ∂ ψ ∂ t , A ^ ψ ) + ( ψ , A ^ ∂ ψ ∂ t ) + ( ψ , ∂ A ^ ∂ t ψ ) = ( H ^ ψ i ℏ , A ^ ψ ) + ( ψ , A ^ H ^ ψ i ℏ ) + ( ψ , ∂ A ^ ∂ t ψ ) = − 1 i ℏ ( ψ , H ^ A ^ ψ ) + 1 i ℏ ( ψ , A ^ H ^ ψ ) + ( ψ , ∂ A ^ ∂ t ψ ) = 1 i ℏ ( ψ , [ A ^ , H ^ ] ψ ) + ( ψ , ∂ A ^ ∂ t ψ ) = 1 i ℏ [ A ^ , H ^ ] ‾ + ∂ A ^ ∂ t ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A}(t) = \left( \frac{\partial \psi}{\partial t} , \hat{A} \psi \right) + \left( \psi , \hat{A} \frac{\partial \psi}{\partial t} \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = \left( \frac{\hat{H} \psi}{\mathrm{i}\hbar} , \hat{A} \psi \right) + \left( \psi , \hat{A} \frac{\hat{H} \psi}{\mathrm{i}\hbar} \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = -\frac{1}{\mathrm{i}\hbar} \left( \psi , \hat{H} \hat{A} \psi \right) + \frac{1}{\mathrm{i}\hbar} \left( \psi , \hat{A} \hat{H} \psi \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( \psi , [\hat{A} , \hat{H}] \psi \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A} , \hat{H}]} + \overline{\frac{\partial \hat{A}}{\partial t}} d t d A ˉ ( t ) = ( ∂ t ∂ ψ , A ^ ψ ) + ( ψ , A ^ ∂ t ∂ ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = ( i ℏ H ^ ψ , A ^ ψ ) + ( ψ , A ^ i ℏ H ^ ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = − i ℏ 1 ( ψ , H ^ A ^ ψ ) + i ℏ 1 ( ψ , A ^ H ^ ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = i ℏ 1 ( ψ , [ A ^ , H ^ ] ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = i ℏ 1 [ A ^ , H ^ ] + ∂ t ∂ A ^
如果 A ^ \hat{A} A ^ t t t ∂ A ^ ∂ t = 0 \frac{\partial \hat{A}}{\partial t} = 0 ∂ t ∂ A ^ = 0
d d t A ˉ = 1 i ℏ [ A ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A} = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A} , \hat{H}]} d t d A ˉ = i ℏ 1 [ A ^ , H ^ ]
因此,若
[ A ^ , H ^ ] = 0 [\hat{A} , \hat{H}] = 0 [ A ^ , H ^ ] = 0
则
d d t A ˉ = 0 \frac{\mathrm{d}}{\mathrm{d}t} \bar{A} = 0 d t d A ˉ = 0
即这种力学量在任何态 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) 平均值都不随时间改变 。进一步考虑其概率分布,因为 [ A ^ , H ^ ] = 0 [\hat{A} , \hat{H}] = 0 [ A ^ , H ^ ] = 0 H ^ \hat{H} H ^ A ^ \hat{A} A ^ ψ k \psi_k ψ k
H ^ ψ k = E k ψ k , A ^ ψ k = A k ψ k \hat{H} \psi_k = E_k \psi_k \ , \kern 1em \hat{A} \psi_k = A_k \psi_k H ^ ψ k = E k ψ k , A ^ ψ k = A k ψ k
这样,体系的任何(已归一化的)态 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) ψ k \psi_k ψ k
ψ ( r ⃗ , t ) = ∑ k a k ( t ) ψ k ( r ⃗ ) \psi(\vec{r},t) = \sum_k a_k(t)\psi_k(\vec{r}) ψ ( r , t ) = k ∑ a k ( t ) ψ k ( r )
展开系数 a k ( t ) = ( ψ k , ψ ) a_k(t) = (\psi_k , \psi) a k ( t ) = ( ψ k , ψ ) ψ \psi ψ t t t A A A A k A_k A k ∣ a k ( t ) ∣ 2 |a_k(t)|^2 ∣ a k ( t ) ∣ 2
d d t ∣ a k ( t ) ∣ 2 = d d t [ a k ∗ ( t ) a k ( t ) ] = a k ( t ) d a k ∗ ( t ) d t + a k ∗ ( t ) d a k ( t ) d t = ( ψ k , ψ ) ( ∂ ψ ∂ t , ψ k ) + 复共轭项 = ( ψ k , ψ ) ( H ^ ψ i ℏ , ψ k ) + 复共轭项 = − 1 i ℏ ( ψ k , ψ ) ( H ^ ψ , ψ k ) + 复共轭项 = − 1 i ℏ ( ψ k , ψ ) ( ψ , H ^ ψ k ) + 复共轭项 = − E k i ℏ ( ψ k , ψ ) ( ψ , ψ k ) + 复共轭项 = − E k i ℏ ∣ ( ψ k , ψ ) ∣ 2 + 复共轭项 = 0 \frac{\mathrm{d}}{\mathrm{d}t} |a_k(t)|^2 = \frac{\mathrm{d}}{\mathrm{d}t} [a_k^(t) a_k(t)] = a_k(t) \frac{\mathrm{d}a_k^ (t)}{\mathrm{d}t} + a_k^*(t) \frac{\mathrm{d}a_k(t)}{\mathrm{d}t} \ \ \ = (\psi_k , \psi) \left( \frac{\partial \psi}{\partial t} , \psi_k \right) + 复共轭项 \ \ \ = (\psi_k , \psi) \left( \frac{\hat{H} \psi}{\mathrm{i}\hbar} , \psi_k \right) + 复共轭项 \ \ \ = -\frac{1}{\mathrm{i}\hbar} (\psi_k , \psi) (\hat{H} \psi , \psi_k) + 复共轭项 \ \ \ = -\frac{1}{\mathrm{i}\hbar} (\psi_k , \psi) (\psi , \hat{H} \psi_k) + 复共轭项 \ \ \ = -\frac{E_k}{\mathrm{i}\hbar} (\psi_k , \psi) (\psi , \psi_k) + 复共轭项 \ \ \ = -\frac{E_k}{\mathrm{i}\hbar} \left| (\psi_k , \psi) \right|^2 + 复共轭项 \ \ \ = 0 d t d ∣ a k ( t ) ∣ 2 = d t d [ a k ∗ ( t ) a k ( t )] = a k ( t ) d t d a k ∗ ( t ) + a k ∗ ( t ) d t d a k ( t ) = ( ψ k , ψ ) ( ∂ t ∂ ψ , ψ k ) + 复共轭项 = ( ψ k , ψ ) ( i ℏ H ^ ψ , ψ k ) + 复共轭项 = − i ℏ 1 ( ψ k , ψ ) ( H ^ ψ , ψ k ) + 复共轭项 = − i ℏ 1 ( ψ k , ψ ) ( ψ , H ^ ψ k ) + 复共轭项 = − i ℏ E k ( ψ k , ψ ) ( ψ , ψ k ) + 复共轭项 = − i ℏ E k ∣ ( ψ k , ψ ) ∣ 2 + 复共轭项 = 0
故 A A A 概率分布不随时间改变 。
对于Hamilton量 H ^ \hat{H} H ^ [ A ^ , H ^ ] = 0 [\hat{A},\hat{H}]=0 [ A ^ , H ^ ] = 0 A ^ \hat{A} A ^ H ^ \hat{H} H ^ 对易 ,则在体系的任意态(定态或非定态)上, A A A 平均值及其取值概率分布都不随时间改变 。量子力学把这些在体系的任意状态上的平均值和取值概率分布都不随时间改变的力学量,称为该体系的守恒量 。
如果体系的Hamilton量不显含时间 t t t ∂ H ^ ∂ t = 0 \frac{\partial \hat{H}}{\partial t} = 0 ∂ t ∂ H ^ = 0 H ^ \hat{H} H ^ 对易守恒量完全集 (a complete set of commuting conserved observables,简记为CSCCO)。
包括 H ^ \hat{H} H ^ 定态 ,所相应的量子数为好量子数 ,任意波函数 ψ \psi ψ ∣ a α ∣ 2 |a_\alpha|^2 ∣ a α ∣ 2
以三维各向同性谐振子为例,CSCCO可取为 { H ^ , L ^ 2 , L ^ z } { \hat{H} , \hat{L}^2 , \hat{L}_z } { H ^ , L ^ 2 , L ^ z } L ^ z \hat{L}_z L ^ z L ^ x \hat{L}_x L ^ x L ^ y \hat{L}_y L ^ y { H ^ x , H ^ y , H ^ z } { \hat{H}_x , \hat{H}_y , \hat{H}_z } { H ^ x , H ^ y , H ^ z }
与经典力学守恒量不同,量子体系的守恒量并不一定取确定值,即体系的状态并不一定就是某个守恒量的本征态,可以保证的只是守恒量的平均值及其取值概率分布都不随时间改变。
即使是在定态(能量本征态)上,守恒量也不一定取确定值,定态只能保证能量取确定值。
若初始时刻体系处于守恒量 A ^ \hat{A} A ^ 保持在该本征态 ,守恒量将取确定值。由于守恒量具有此特点,它的量子数称为好量子数 。
若初始时刻体系并不处于守恒量 A ^ \hat{A} A ^ A ^ \hat{A} A ^ A ^ \hat{A} A ^
量子力学中习惯用描述力学量本征值的量子数来标志状态,但非守恒量的量子数不适合描述状态,只有守恒量的量子数才是描述状态的好量子数。
由于量子体系的各守恒量只要求与Hamilton量 H ^ \hat{H} H ^
定态 是体系的一种特殊的状态,即能量本征态 ;而守恒量 则是体系的一种特殊的力学量,它与体系的Hamilton量对易。
在定态 上,一切力学量 (只要不显含时间 t t t
而守恒量 在一切状态 上(不管是否是定态)的平均值和取值概率分布都不随时间变化。
如果体系具有两个互相不对易的守恒量 F ^ , G ^ \hat{F},\hat{G} F ^ , G ^ [ F ^ , H ^ ] = [ G ^ , H ^ ] = 0 [\hat{F},\hat{H}] = [\hat{G},\hat{H}] = 0 [ F ^ , H ^ ] = [ G ^ , H ^ ] = 0 [ F ^ , G ^ ] ≠ 0 [\hat{F},\hat{G}] \ne 0 [ F ^ , G ^ ] = 0 简并 的。
在一般情况下,当能级出现简并时,可以根据对体系对称性的分析,找出其守恒量。然后要求能量本征态同时又是包含 H ^ \hat{H} H ^
由于 [ F ^ , H ^ ] = 0 [\hat{F},\hat{H}] = 0 [ F ^ , H ^ ] = 0 F ^ \hat{F} F ^ H ^ \hat{H} H ^ ψ \psi ψ
H ^ ψ = E ψ , F ^ ψ = λ ψ \hat{H} \psi = E \psi \ , \kern 1em \hat{F} \psi = \lambda \psi H ^ ψ = E ψ , F ^ ψ = λ ψ
考虑到 [ G ^ , H ^ ] = 0 [\hat{G},\hat{H}] = 0 [ G ^ , H ^ ] = 0
H ^ ( G ^ ψ ) = H ^ G ^ ψ = G ^ H ^ ψ = G ^ E ψ = E ( G ^ ψ ) \hat{H} (\hat{G} \psi) = \hat{H} \hat{G} \psi = \hat{G} \hat{H} \psi = \hat{G} E \psi = E (\hat{G} \psi) H ^ ( G ^ ψ ) = H ^ G ^ ψ = G ^ H ^ ψ = G ^ E ψ = E ( G ^ ψ )
即 G ^ ψ \hat{G}\psi G ^ ψ H ^ \hat{H} H ^ E E E [ F ^ , G ^ ] ≠ 0 [\hat{F},\hat{G}] \ne 0 [ F ^ , G ^ ] = 0
F ^ ( G ^ ψ ) = F ^ G ^ ψ ≠ G ^ F ^ ψ = G ^ λ ψ = λ G ^ ψ \hat{F} (\hat{G} \psi) = \hat{F} \hat{G} \psi \ne \hat{G} \hat{F} \psi = \hat{G} \lambda \psi = \lambda \hat{G} \psi F ^ ( G ^ ψ ) = F ^ G ^ ψ = G ^ F ^ ψ = G ^ λ ψ = λ G ^ ψ
即 G ^ ψ \hat{G}\psi G ^ ψ F ^ \hat{F} F ^ ψ \psi ψ F ^ \hat{F} F ^ G ^ ψ \hat{G}\psi G ^ ψ ψ \psi ψ H ^ \hat{H} H ^ E E E
如果体系有一个守恒量 F ^ \hat{F} F ^ E E E ψ E \psi_E ψ E ψ E \psi_E ψ E F ^ \hat{F} F ^
这是因为
H ^ ( F ^ ψ E ) = H ^ F ^ ψ E = F ^ H ^ ψ E = F ^ E ψ E = E ( F ^ ψ E ) \hat{H} (\hat{F} \psi_E) = \hat{H} \hat{F} \psi_E = \hat{F} \hat{H} \psi_E = \hat{F} E \psi_E = E (\hat{F} \psi_E) H ^ ( F ^ ψ E ) = H ^ F ^ ψ E = F ^ H ^ ψ E = F ^ E ψ E = E ( F ^ ψ E )
即 ψ E \psi_E ψ E H ^ \hat{H} H ^ E E E E E E F ^ ψ E \hat{F}\psi_E F ^ ψ E ψ E \psi_E ψ E λ \lambda λ F ^ ψ E = λ ψ E \hat{F} \psi_E = \lambda \psi_E F ^ ψ E = λ ψ E ψ E \psi_E ψ E F ^ \hat{F} F ^
对于上述的“一般”,虽然 [ F ^ , G ^ ] ≠ 0 [\hat{F},\hat{G}] \ne 0 [ F ^ , G ^ ] = 0 F ^ \hat{F} F ^ G ^ \hat{G} G ^ [ F ^ , G ^ ] ψ 0 = 0 [\hat{F},\hat{G}]\psi_0 = 0 [ F ^ , G ^ ] ψ 0 = 0 ψ 0 \psi_0 ψ 0 G ^ ψ 0 \hat{G}\psi_0 G ^ ψ 0 ψ 0 \psi_0 ψ 0 ψ 0 \psi_0 ψ 0 [ F ^ , G ^ ] [\hat{F},\hat{G}] [ F ^ , G ^ ]
例如:中心力场下, L ⃗ ^ \hat{\vec{L}} L ^ L ^ x , L ^ y , L ^ z \hat{L}_x , \hat{L}_y , \hat{L}_z L ^ x , L ^ y , L ^ z s s s l = 0 l=0 l = 0 L x , L y , L z L_x , L_y , L_z L x , L y , L z 0 0 0 L ^ x ψ s = L ^ y ψ s = L ^ z ψ s = 0 \hat{L}_x \psi_s = \hat{L}_y \psi_s = \hat{L}_z \psi_s = 0 L ^ x ψ s = L ^ y ψ s = L ^ z ψ s = 0 [ L ^ x , L ^ y ] ψ s = [ L ^ y , L ^ z ] ψ s = [ L ^ z , L ^ x ] ψ s = 0 [\hat{L}_x , \hat{L}_y] \psi_s = [\hat{L}_y , \hat{L}_z] \psi_s = [\hat{L}_z , \hat{L}_x] \psi_s = 0 [ L ^ x , L ^ y ] ψ s = [ L ^ y , L ^ z ] ψ s = [ L ^ z , L ^ x ] ψ s = 0 ψ s \psi_s ψ s l = 0 l=0 l = 0
位力定理可以描述当体系处于定态 下时平均值关于时间的变化。
设粒子处于势场 V ( r ⃗ ) V(\vec{r}) V ( r )
H ^ = p ⃗ ^ 2 2 m + V ( r ⃗ ) \hat{H} = \frac{\hat{\vec{p}}^2}{2m} + V(\vec{r}) H ^ = 2 m p ^ 2 + V ( r )
则粒子的动能算符 T ^ = p ⃗ ^ 2 / ( 2 m ) \hat{T} = \hat{\vec{p}}^2 /(2m) T ^ = p ^ 2 / ( 2 m ) 定态 上的平均值为
T ˉ = 1 2 r ⃗ ⋅ ∇ V ‾ \bar{T} = \frac12 \overline{\vec{r} \cdot \nabla V } T ˉ = 2 1 r ⋅ ∇ V
先考虑 r ⃗ ⋅ p ⃗ \vec{r} \cdot \vec{p}, r ⋅ p ∂ ∂ t ( r ⃗ ^ ⋅ p ⃗ ^ ) = 0 \frac{\partial}{\partial t} (\hat{\vec{r}}\cdot\hat{\vec{p}})=0 ∂ t ∂ ( r ^ ⋅ p ^ ) = 0 r ⃗ ^ ⋅ p ⃗ ^ \hat{\vec{r}} \cdot \hat{\vec{p}}, r ^ ⋅ p ^ 1 2 ( r ⃗ ^ ⋅ p ⃗ ^ + p ⃗ ^ ⋅ r ⃗ ^ ) \frac12(\hat{\vec{r}}\cdot\hat{\vec{p}} + \hat{\vec{p}}\cdot\hat{\vec{r}}) 2 1 ( r ^ ⋅ p ^ + p ^ ⋅ r ^ ) A ^ \hat{A} A ^
d d t A ˉ = 1 i ℏ [ A ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A} = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A} , \hat{H}]} d t d A ˉ = i ℏ 1 [ A ^ , H ^ ]
可知
d d t r ⃗ ⋅ p ⃗ ‾ = 1 i ℏ [ r ⃗ ^ ⋅ p ⃗ ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \overline{\vec{r}\cdot\vec{p}} = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{H}]} d t d r ⋅ p = i ℏ 1 [ r ^ ⋅ p ^ , H ^ ]
其中
[ r ⃗ ^ ⋅ p ⃗ ^ , H ^ ] ‾ = [ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 2 m + V ( r ⃗ ) ] ‾ = 1 2 m [ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 ] ‾ + [ r ⃗ ^ ⋅ p ⃗ ^ , V ( r ⃗ ) ] ‾ \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{H}]} = \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \frac{\hat{\vec{p}}^2}{2m} + V(\vec{r})]} \ \ \ = \frac{1}{2m} \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{\vec{p}}^2]} + \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , V(\vec{r})]} [ r ^ ⋅ p ^ , H ^ ] = [ r ^ ⋅ p ^ , 2 m p ^ 2 + V ( r )] = 2 m 1 [ r ^ ⋅ p ^ , p ^ 2 ] + [ r ^ ⋅ p ^ , V ( r )]
其中的第一个对易关系可通过分量展开考虑
[ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 ] = r ⃗ ^ ⋅ [ p ⃗ ^ , p ⃗ ^ 2 ] + [ r ⃗ ^ , p ⃗ ^ 2 ] ⋅ p ⃗ ^ = [ r ⃗ ^ , p ⃗ ^ 2 ] ⋅ p ⃗ ^ = ( [ x ^ , p x 2 ^ ] i ⃗ + [ y ^ , p y 2 ^ ] j ⃗ + [ z ^ , p z 2 ^ ] k ⃗ ) ⋅ p ⃗ ^ = { ( p ^ x [ x ^ , p ^ x ] + [ x ^ , p ^ x ] p ^ x ) i ⃗ + ( p ^ y [ y ^ , p ^ y ] + [ y ^ , p ^ y ] p ^ y ) j ⃗ + ( p ^ z [ z ^ , p ^ z ] + [ z ^ , p ^ z ] p ^ z ) k ⃗ } ⋅ p ⃗ ^ = 2 i ℏ ( p ^ x i ⃗ + p ^ y j ⃗ + p ^ z k ⃗ ) ⋅ p ⃗ ^ = 2 i ℏ p ⃗ ^ 2 [\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{\vec{p}}^2] = \hat{\vec{r}}\cdot [\hat{\vec{p}} , \hat{\vec{p}}^2] + [\hat{\vec{r}} , \hat{\vec{p}}^2] \cdot\hat{\vec{p}} = [\hat{\vec{r}} , \hat{\vec{p}}^2] \cdot\hat{\vec{p}} \ \ \ = \left( [\hat{x},\hat{p_x^2}] \vec{i} + [\hat{y},\hat{p_y^2}] \vec{j} + [\hat{z},\hat{p_z^2}] \vec{k} \right) \cdot\hat{\vec{p}} \ \ \ = \left{ \left( \hat{p}_x [\hat{x},\hat{p}_x] + [\hat{x},\hat{p}_x] \hat{p}_x \right) \vec{i} + \left( \hat{p}_y [\hat{y},\hat{p}_y] + [\hat{y},\hat{p}_y] \hat{p}_y \right) \vec{j} + \left( \hat{p}_z [\hat{z},\hat{p}_z] + [\hat{z},\hat{p}_z] \hat{p}_z \right) \vec{k} \right} \cdot\hat{\vec{p}} \ \ \ = 2\mathrm{i} \hbar \left( \hat{p}_x \vec{i} + \hat{p}_y \vec{j} + \hat{p}_z \vec{k} \right) \cdot\hat{\vec{p}} \ \ \ = 2\mathrm{i} \hbar \hat{\vec{p}}^2 [ r ^ ⋅ p ^ , p ^ 2 ] = r ^ ⋅ [ p ^ , p ^ 2 ] + [ r ^ , p ^ 2 ] ⋅ p ^ = [ r ^ , p ^ 2 ] ⋅ p ^ = ( [ x ^ , p x 2 ^ ] i + [ y ^ , p y 2 ^ ] j + [ z ^ , p z 2 ^ ] k ) ⋅ p ^ = { ( p ^ x [ x ^ , p ^ x ] + [ x ^ , p ^ x ] p ^ x ) i + ( p ^ y [ y ^ , p ^ y ] + [ y ^ , p ^ y ] p ^ y ) j + ( p ^ z [ z ^ , p ^ z ] + [ z ^ , p ^ z ] p ^ z ) k } ⋅ p ^ = 2 i ℏ ( p ^ x i + p ^ y j + p ^ z k ) ⋅ p ^ = 2 i ℏ p ^ 2
第二个对易关系可通过在坐标表象下作用波函数考虑
[ r ⃗ ^ ⋅ p ⃗ ^ , V ( r ⃗ ) ] ψ = − i ℏ [ r ⃗ ⋅ ∇ , V ( r ⃗ ) ] ψ = − i ℏ r ⃗ ⋅ [ ∇ , V ( r ⃗ ) ] ψ − i ℏ [ r ⃗ , V ( r ⃗ ) ] ⋅ ∇ ψ = − i ℏ r ⃗ ⋅ { ∇ ( V ( r ⃗ ) ψ ) − V ( r ⃗ ) ∇ ψ } = − i ℏ r ⃗ ⋅ ( ∇ V ( r ⃗ ) ) ψ [\hat{\vec{r}}\cdot\hat{\vec{p}} , V(\vec{r})] \psi = -\mathrm{i} \hbar [\vec{r}\cdot\nabla , V(\vec{r})] \psi \ \ \ = -\mathrm{i} \hbar \vec{r}\cdot [\nabla , V(\vec{r})] \psi -\mathrm{i} \hbar [\vec{r} , V(\vec{r})] \cdot\nabla \psi \ \ \ = -\mathrm{i} \hbar \vec{r}\cdot \left{ \nabla\left(V(\vec{r})\psi\right) - V(\vec{r}) \nabla\psi \right} \ \ \ = -\mathrm{i} \hbar \vec{r}\cdot \left( \nabla V(\vec{r}) \right) \psi [ r ^ ⋅ p ^ , V ( r )] ψ = − i ℏ [ r ⋅ ∇ , V ( r )] ψ = − i ℏ r ⋅ [ ∇ , V ( r )] ψ − i ℏ [ r , V ( r )] ⋅ ∇ ψ = − i ℏ r ⋅ { ∇ ( V ( r ) ψ ) − V ( r ) ∇ ψ } = − i ℏ r ⋅ ( ∇ V ( r ) ) ψ
故
[ r ⃗ ^ ⋅ p ⃗ ^ , H ^ ] ‾ = 1 2 m [ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 ] ‾ + [ r ⃗ ^ ⋅ p ⃗ ^ , V ( r ⃗ ) ] ‾ = 1 2 m 2 i ℏ p ⃗ 2 ‾ + − i ℏ r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ = i ℏ [ 2 p ⃗ 2 2 m ‾ − r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ ] = i ℏ [ 2 T ‾ − r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ ] \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{H}]} = \frac{1}{2m} \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{\vec{p}}^2]} + \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , V(\vec{r})]} \ \ \ = \frac{1}{2m} \overline{2\mathrm{i} \hbar \vec{p}^2} + \overline{-\mathrm{i} \hbar \vec{r}\cdot \nabla V(\vec{r})} \ \ \ = \mathrm{i} \hbar \left[ 2 \overline{\frac{\vec{p}^2}{2m}} - \overline{\vec{r}\cdot\nabla V(\vec{r})} \right] \ \ \ = \mathrm{i} \hbar \left[ 2 \overline{T} - \overline{\vec{r}\cdot\nabla V(\vec{r})} \right] [ r ^ ⋅ p ^ , H ^ ] = 2 m 1 [ r ^ ⋅ p ^ , p ^ 2 ] + [ r ^ ⋅ p ^ , V ( r )] = 2 m 1 2 i ℏ p 2 + − i ℏ r ⋅ ∇ V ( r ) = i ℏ [ 2 2 m p 2 − r ⋅ ∇ V ( r ) ] = i ℏ [ 2 T − r ⋅ ∇ V ( r ) ]
对于定态,有
d d t r ⃗ ⋅ p ⃗ ‾ = 0 \frac{\mathrm{d}}{\mathrm{d}t} \overline{\vec{r}\cdot\vec{p}} = 0 d t d r ⋅ p = 0
故
2 T ‾ − r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ = 0 2 \overline{T} - \overline{\vec{r}\cdot\nabla V(\vec{r})} = 0 2 T − r ⋅ ∇ V ( r ) = 0
若 V ( r ⃗ ) V(\vec{r}) V ( r ) x , y , z x,y,z x , y , z n n n V ( c x , c y , c z ) = c n V ( x , y , z ) V(cx,cy,cz) = c^n V(x,y,z) V ( c x , cy , cz ) = c n V ( x , y , z ) c c c
r ⃗ ⋅ ∇ V ( r ⃗ ) = n V ( r ⃗ ) \vec{r}\cdot\nabla V(\vec{r}) = n V(\vec{r}) r ⋅ ∇ V ( r ) = nV ( r )
证明可见杨利军老师微积分A2第二次习题课 第6题。
故
2 T ˉ = n V ˉ 2 \bar{T} = n \bar{V} 2 T ˉ = n V ˉ
如对于谐振子势 V ( r ⃗ ) = 1 2 m ω 2 r 2 V(\vec{r}) = \frac12 m\omega^2 r^2 V ( r ) = 2 1 m ω 2 r 2 n = 2 n=2 n = 2 T ˉ = V ˉ \bar{T} = \bar{V} T ˉ = V ˉ V ( r ⃗ ) = − k Z e 2 r V(\vec{r}) = -\frac{kZe^2}{r} V ( r ) = − r k Z e 2 n = − 1 n=-1 n = − 1 T ˉ = − 1 2 V ˉ \bar{T} = -\frac12 \bar{V} T ˉ = − 2 1 V ˉ E ˉ = T ˉ + V ˉ = 1 2 V ˉ \bar{E} = \bar{T} + \bar{V} = \frac12 \bar{V} E ˉ = T ˉ + V ˉ = 2 1 V ˉ
这里的图像 (picture)也叫绘景 ,亦称表象 (representation)。由于状态和力学量本身并不能直接测量,能直接测量的是力学量的平均值,因此可以用不同方式描述状态和力学量随时间的演化 ,只要保证力学量的平均值不因描述方式的不同而改变取值即可。
态矢 ψ ( t ) \psi(t) ψ ( t ) 随时间演化 ,其变化遵守Schrödinger方程,力学量算符 (不显含时间 t t t 与时间无关 ,即把力学量平均值及测值概率分布随时间的演化完全归之于波函数的演化,这种描述方式称为Schrödinger图像 。即
A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ) ) \bar{A}(t) = (\psi(t) , \hat{A} \psi(t)) A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ))
其中 ψ ( t ) \psi(t) ψ ( t )
i ℏ ∂ ∂ t ψ ( t ) = H ^ ψ ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(t) = \hat{H} \psi(t) i ℏ ∂ t ∂ ψ ( t ) = H ^ ψ ( t )
由此可以得到
d d t A ˉ ( t ) = 1 i ℏ [ A ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A}(t) = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A},\hat{H}]} d t d A ˉ ( t ) = i ℏ 1 [ A ^ , H ^ ]
态矢 ψ \psi ψ 不随时间变化 ,而力学量算符随时间变化 ,其变化遵守Heisenberg方程,即把力学量平均值及测值概率分布随时间的演化完全归之于算符的演化,这种描述方式称为Heisenberg图像 。即
A ˉ ( t ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ) ) \bar{A}(t) = (\psi(0) , \hat{A}(t) \psi(0)) A ˉ ( t ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ))
其中 A ^ ( t ) \hat{A}(t) A ^ ( t ) Heisenberg方程
d d t A ^ ( t ) = 1 i ℏ [ A ^ ( t ) , H ^ ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}(t) = \frac{1}{\mathrm{i}\hbar} [\hat{A}(t) , \hat{H}] d t d A ^ ( t ) = i ℏ 1 [ A ^ ( t ) , H ^ ]
引入时间演化算符 U ^ ( t , 0 ) = exp ( − i ℏ H ^ t ) \hat{U}(t,0) = \exp(-\frac{\mathrm{i}}{\hbar}\hat{H}t) U ^ ( t , 0 ) = exp ( − ℏ i H ^ t ) 0 0 0 t t t U ^ ( t , 0 ) ψ ( 0 ) = ψ ( t ) \hat{U}(t,0) \psi(0) = \psi(t) U ^ ( t , 0 ) ψ ( 0 ) = ψ ( t ) A ^ ( t ) \hat{A}(t) A ^ ( t )
A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e i ℏ H ^ t A ^ e − i ℏ H ^ t \hat{A}(t) = \hat{U}(t,0)^+\ \hat{A}\ \hat{U}(t,0) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \hat{A}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e ℏ i H ^ t A ^ e − ℏ i H ^ t
对于Schrödinger方程
i ℏ ∂ ∂ t ψ ( t ) = H ^ ψ ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(t) = \hat{H} \psi(t) i ℏ ∂ t ∂ ψ ( t ) = H ^ ψ ( t )
当 H ^ \hat{H} H ^ t t t ψ ( t ) \psi(t) ψ ( t )
ψ ( t ) = U ^ ( t , 0 ) ψ ( 0 ) \psi(t) = \hat{U}(t,0) \psi(0) ψ ( t ) = U ^ ( t , 0 ) ψ ( 0 )
其中 U ^ ( t 2 , t 1 ) \hat{U}(t_2,t_1) U ^ ( t 2 , t 1 ) t 1 t_1 t 1 t 2 t_2 t 2 U ^ ( 0 , 0 ) = 1 \hat{U}(0,0) = 1 U ^ ( 0 , 0 ) = 1
i ℏ ∂ ∂ t U ^ ( t , 0 ) ψ ( 0 ) = H ^ U ^ ( t , 0 ) ψ ( 0 ) \mathrm{i}\hbar \frac{\partial}{\partial t} \hat{U}(t,0) \psi(0) = \hat{H} \hat{U}(t,0) \psi(0) i ℏ ∂ t ∂ U ^ ( t , 0 ) ψ ( 0 ) = H ^ U ^ ( t , 0 ) ψ ( 0 )
由于 ψ ( 0 ) \psi(0) ψ ( 0 )
i ℏ ∂ ∂ t U ^ ( t , 0 ) = H ^ U ^ ( t , 0 ) \mathrm{i}\hbar \frac{\partial}{\partial t} \hat{U}(t,0) = \hat{H} \hat{U}(t,0) i ℏ ∂ t ∂ U ^ ( t , 0 ) = H ^ U ^ ( t , 0 )
结合初始条件 U ^ ( 0 , 0 ) = 1 \hat{U}(0,0) = 1 U ^ ( 0 , 0 ) = 1
U ^ ( t , 0 ) = e − i ℏ H ^ t \hat{U}(t,0) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} U ^ ( t , 0 ) = e − ℏ i H ^ t
可以验证 U ^ ( t , 0 ) \hat{U}(t,0) U ^ ( t , 0 )
U ^ ( t , 0 ) + U ^ ( t , 0 ) = U ^ ( t , 0 ) U ^ ( t , 0 ) + = I \hat{U}(t,0)^+ \hat{U}(t,0) = \hat{U}(t,0) \hat{U}(t,0)^+ = I U ^ ( t , 0 ) + U ^ ( t , 0 ) = U ^ ( t , 0 ) U ^ ( t , 0 ) + = I
从而可以保证概率守恒
( ψ ( t ) , ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , ψ ( 0 ) ) (\ \psi(t) , \psi(t)\ ) = (\ \hat{U}(t,0)\psi(0) , \hat{U}(t,0)\psi(0)\ ) = (\ \psi(0) , \hat{U}(t,0)^+\hat{U}(t,0)\psi(0)\ ) = (\ \psi(0) , \psi(0)\ ) ( ψ ( t ) , ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , ψ ( 0 ) )
考虑力学量 A A A
A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ) ) \bar{A}(t) = (\ \psi(t) , \hat{A} \psi(t)\ ) \ \ \ = (\ \hat{U}(t,0)\psi(0) , \hat{A}\hat{U}(t,0)\psi(0)\ ) \ \ \ = (\ \psi(0) , \hat{U}(t,0)^+\hat{A}\hat{U}(t,0)\psi(0)\ ) \ \ \ = (\ \psi(0) , \hat{A}(t)\psi(0)\ ) A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ) )
其中
A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e i ℏ H ^ t A ^ e − i ℏ H ^ t \hat{A}(t) = \hat{U}(t,0)^+\ \hat{A}\ \hat{U}(t,0) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \hat{A}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e ℏ i H ^ t A ^ e − ℏ i H ^ t
考虑其随时间的变化(在下式推导中,用到了 U ^ U ^ + = I , U ^ + H ^ U ^ = H ^ , U ^ + A ^ U ^ = A ^ ( t ) \hat{U}\hat{U}^+ = I\ ,\ \hat{U}^+\hat{H}\hat{U} = \hat{H}\ ,\ \hat{U}^+\hat{A}\hat{U} = \hat{A}(t) U ^ U ^ + = I , U ^ + H ^ U ^ = H ^ , U ^ + A ^ U ^ = A ^ ( t )
d d t A ^ ( t ) = [ d d t U ^ ( t , 0 ) + ] A ^ U ^ ( t , 0 ) + U ^ ( t , 0 ) + A ^ [ d d t U ^ ( t , 0 ) ] = 1 i ℏ ( − U ^ + H ^ A ^ U ^ + U ^ + A ^ H ^ U ^ ) = 1 i ℏ ( − U ^ + H ^ U ^ U ^ + A ^ U ^ + U ^ + A ^ U ^ U ^ + H ^ U ^ ) = 1 i ℏ ( − H ^ A ^ ( t ) + A ^ ( t ) H ^ ) = 1 i ℏ [ A ^ ( t ) , H ^ ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}(t) = \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}(t,0)^+ \right] \hat{A}\ \hat{U}(t,0) + \hat{U}(t,0)^+\ \hat{A} \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}(t,0) \right] \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}^+\hat{H}\hat{A}\hat{U} + \hat{U}^+\hat{A}\hat{H}\hat{U} \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}^+\hat{H}\hat{U}\hat{U}^+\hat{A}\hat{U} + \hat{U}^+\hat{A}\hat{U}\hat{U}^+\hat{H}\hat{U} \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{H}\hat{A}(t) + \hat{A}(t)\hat{H} \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} [\hat{A}(t) , \hat{H}] d t d A ^ ( t ) = [ d t d U ^ ( t , 0 ) + ] A ^ U ^ ( t , 0 ) + U ^ ( t , 0 ) + A ^ [ d t d U ^ ( t , 0 ) ] = i ℏ 1 ( − U ^ + H ^ A ^ U ^ + U ^ + A ^ H ^ U ^ ) = i ℏ 1 ( − U ^ + H ^ U ^ U ^ + A ^ U ^ + U ^ + A ^ U ^ U ^ + H ^ U ^ ) = i ℏ 1 ( − H ^ A ^ ( t ) + A ^ ( t ) H ^ ) = i ℏ 1 [ A ^ ( t ) , H ^ ]
将Schrödinegr图像中的态与算符分别用 ψ ( S ) , A ^ ( S ) \psi^{(S)},\hat{A}^{(S)} ψ ( S ) , A ^ ( S ) ψ ( H ) , A ^ ( H ) \psi^{(H)},\hat{A}^{(H)} ψ ( H ) , A ^ ( H )
ψ ( H ) = e i ℏ H ^ t ψ ( S ) ( t ) = ψ ( S ) ( 0 ) A ^ ( H ) ( t ) = e i ℏ H ^ t A ^ ( S ) e − i ℏ H ^ t \psi^{(H)} = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \psi^{(S)}(t) = \psi^{(S)}(0) \ \ \ \hat{A}^{(H)}(t) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \hat{A}^{(S)}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} ψ ( H ) = e ℏ i H ^ t ψ ( S ) ( t ) = ψ ( S ) ( 0 ) A ^ ( H ) ( t ) = e ℏ i H ^ t A ^ ( S ) e − ℏ i H ^ t
在Schrödinegr图像与Heisenberg图像中守恒量算符的形式相同,如 H ^ ( S ) = H ^ ( H ) \hat{H}^{(S)} = \hat{H}^{(H)} H ^ ( S ) = H ^ ( H )
将Hamilton算符表示为两个算符之和,即
H ^ = H ^ 0 + H ^ I ( t ) \hat{H} = \hat{H}_0 + \hat{H}_I(t) H ^ = H ^ 0 + H ^ I ( t )
其中 H ^ 0 \hat{H}_0 H ^ 0 H ^ I ( t ) \hat{H}_I(t) H ^ I ( t ) U ^ 0 ( t , 0 ) = exp ( − i ℏ H ^ 0 t ) \hat{U}_0(t,0) = \exp(-\frac{\mathrm{i}}{\hbar}\hat{H}_0t) U ^ 0 ( t , 0 ) = exp ( − ℏ i H ^ 0 t )
与Schrödinger图像相比,相互作用图像中的态与算符分别表示为
ψ ( I ) ( t ) = U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = e i ℏ H ^ 0 t ψ ( S ) ( t ) A ^ ( I ) ( t ) = U ^ 0 + ( t , 0 ) A ^ ( S ) U ^ 0 ( t , 0 ) = e i ℏ H ^ 0 t A ^ ( S ) e − i ℏ H ^ 0 t \psi^{(I)}(t) = \hat{U}_0^+(t,0)\ \psi^{(S)}(t) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t}\ \psi^{(S)}(t) \ \ \ \hat{A}^{(I)}(t) = \hat{U}_0^+(t,0)\ \hat{A}^{(S)}\ \hat{U}_0(t,0) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t}\ \hat{A}^{(S)}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}_0t} ψ ( I ) ( t ) = U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = e ℏ i H ^ 0 t ψ ( S ) ( t ) A ^ ( I ) ( t ) = U ^ 0 + ( t , 0 ) A ^ ( S ) U ^ 0 ( t , 0 ) = e ℏ i H ^ 0 t A ^ ( S ) e − ℏ i H ^ 0 t
态 ψ ( I ) ( t ) \psi^{(I)}(t) ψ ( I ) ( t )
i ℏ ∂ ∂ t ψ ( I ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi^{(I)}(t) = \hat{H}_I^{(I)}(t) \psi^{(I)}(t) i ℏ ∂ t ∂ ψ ( I ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t )
算符 A ^ ( I ) ( t ) \hat{A}^{(I)}(t) A ^ ( I ) ( t )
d d t A ^ ( I ) ( t ) = 1 i ℏ [ A ^ ( I ) ( t ) , H ^ 0 ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}^{(I)}(t) = \frac{1}{\mathrm{i}\hbar} [\hat{A}^{(I)}(t) , \hat{H}_0] d t d A ^ ( I ) ( t ) = i ℏ 1 [ A ^ ( I ) ( t ) , H ^ 0 ]
力学量 A A A
A ˉ ( t ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) ) \bar{A}(t) = (\ \psi^{(I)}(t) , \hat{A}^{(I)}(t) \psi^{(I)}(t)\ ) A ˉ ( t ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) )
态矢 ψ ( I ) ( t ) \psi^{(I)}(t) ψ ( I ) ( t ) A ^ ( I ) ( t ) \hat{A}^{(I)}(t) A ^ ( I ) ( t )
态矢的演化由相互作用 H ^ I ( t ) \hat{H}_I(t) H ^ I ( t ) H ^ 0 \hat{H}_0 H ^ 0
相互作用图像介于Schrödinger图像和Heisenberg图像之间,在用微扰论来处理问题时有广泛的应用。
首先考虑态 ψ ( I ) ( t ) \psi^{(I)}(t) ψ ( I ) ( t )
i ℏ ∂ ∂ t ψ ( I ) ( t ) = i ℏ ∂ ∂ t [ U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) ] = ( i ℏ ∂ ∂ t e i ℏ H ^ 0 t ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ i ℏ ∂ ∂ t ψ ( S ) ( t ) ] = − ( e i ℏ H ^ 0 t H ^ 0 ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ H ^ ψ ( S ) ( t ) ] = U ^ 0 + ( t , 0 ) ( H ^ − H ^ 0 ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) U ^ 0 ( t , 0 ) U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi^{(I)}(t) = \mathrm{i}\hbar \frac{\partial}{\partial t} \left[ \hat{U}_0^+(t,0)\ \psi^{(S)}(t) \right] \ \ \ = \left( \mathrm{i}\hbar \frac{\partial}{\partial t} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t} \right) \psi^{(S)}(t) + \hat{U}_0^+(t,0) \left[ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi^{(S)}(t) \right] \ \ \ = -\left( \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t} \hat{H}_0 \right) \psi^{(S)}(t) + \hat{U}_0^+(t,0) \left[ \hat{H} \psi^{(S)}(t) \right] \ \ \ = \hat{U}_0^+(t,0) \left( \hat{H} - \hat{H}_0 \right) \psi^{(S)}(t) \ \ \ = \hat{U}_0^+(t,0) \hat{H}_I(t) \psi^{(S)}(t) \ \ \ = \hat{U}_0^+(t,0) \hat{H}_I(t) \hat{U}_0(t,0)\ \hat{U}_0^+(t,0) \psi^{(S)}(t) \ \ \ = \hat{H}_I^{(I)}(t) \psi^{(I)}(t) i ℏ ∂ t ∂ ψ ( I ) ( t ) = i ℏ ∂ t ∂ [ U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) ] = ( i ℏ ∂ t ∂ e ℏ i H ^ 0 t ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ i ℏ ∂ t ∂ ψ ( S ) ( t ) ] = − ( e ℏ i H ^ 0 t H ^ 0 ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ H ^ ψ ( S ) ( t ) ] = U ^ 0 + ( t , 0 ) ( H ^ − H ^ 0 ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) U ^ 0 ( t , 0 ) U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t )
对于力学量算符 A ^ ( I ) ( t ) \hat{A}^{(I)}(t) A ^ ( I ) ( t )
d d t A ^ ( I ) ( t ) = [ d d t U ^ 0 ( t , 0 ) + ] A ^ U ^ 0 ( t , 0 ) + U ^ 0 ( t , 0 ) + A ^ [ d d t U ^ 0 ( t , 0 ) ] = 1 i ℏ ( − U ^ 0 + H ^ 0 A ^ U ^ 0 + U ^ 0 + A ^ H ^ 0 U ^ 0 ) = 1 i ℏ ( − U ^ 0 + H ^ 0 U ^ 0 U ^ 0 + A ^ U ^ 0 + U ^ 0 + A ^ U ^ 0 U ^ 0 + H ^ 0 U ^ 0 ) = 1 i ℏ ( − H ^ 0 A ^ ( I ) ( t ) + A ^ ( I ) ( t ) H ^ 0 ) = 1 i ℏ [ A ^ ( I ) ( t ) , H ^ 0 ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}^{(I)}(t) = \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}_0(t,0)^+ \right] \hat{A}\ \hat{U}_0(t,0) + \hat{U}_0(t,0)^+\ \hat{A} \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}_0(t,0) \right] \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}_0^+\hat{H}_0\hat{A}\hat{U}_0 + \hat{U}_0^+\hat{A}\hat{H}_0\hat{U}_0 \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}_0^+\hat{H}_0\hat{U}_0\hat{U}_0^+\hat{A}\hat{U}_0 + \hat{U}_0^+\hat{A}\hat{U}_0\hat{U}_0^+\hat{H}_0\hat{U}_0 \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{H}_0\hat{A}^{(I)}(t) + \hat{A}^{(I)}(t)\hat{H}_0 \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} [\hat{A}^{(I)}(t) , \hat{H}_0] d t d A ^ ( I ) ( t ) = [ d t d U ^ 0 ( t , 0 ) + ] A ^ U ^ 0 ( t , 0 ) + U ^ 0 ( t , 0 ) + A ^ [ d t d U ^ 0 ( t , 0 ) ] = i ℏ 1 ( − U ^ 0 + H ^ 0 A ^ U ^ 0 + U ^ 0 + A ^ H ^ 0 U ^ 0 ) = i ℏ 1 ( − U ^ 0 + H ^ 0 U ^ 0 U ^ 0 + A ^ U ^ 0 + U ^ 0 + A ^ U ^ 0 U ^ 0 + H ^ 0 U ^ 0 ) = i ℏ 1 ( − H ^ 0 A ^ ( I ) ( t ) + A ^ ( I ) ( t ) H ^ 0 ) = i ℏ 1 [ A ^ ( I ) ( t ) , H ^ 0 ]
对于力学量 A A A
A ˉ ( t ) = ( ψ ( S ) ( t ) , A ^ ψ ( S ) ( t ) ) = ( U ^ 0 ( t , 0 ) ψ ( I ) ( t ) , A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , U ^ 0 ( t , 0 ) + A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) ) \bar{A}(t) = (\ \psi^{(S)}(t) , \hat{A} \psi^{(S)}(t)\ ) \ \ \ = (\ \hat{U}_0(t,0)\psi^{(I)}(t) , \hat{A}\hat{U}_0(t,0)\psi^{(I)}(t)\ ) \ \ \ = (\ \psi^{(I)}(t) , \hat{U}_0(t,0)^+\hat{A}\hat{U}_0(t,0)\psi^{(I)}(t)\ ) \ \ \ = (\ \psi^{(I)}(t) , \hat{A}^{(I)}(t)\psi^{(I)}(t)\ ) A ˉ ( t ) = ( ψ ( S ) ( t ) , A ^ ψ ( S ) ( t ) ) = ( U ^ 0 ( t , 0 ) ψ ( I ) ( t ) , A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , U ^ 0 ( t , 0 ) + A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) )
设体系的状态用 ψ \psi ψ ψ \psi ψ
i ℏ ∂ ∂ t ψ = H ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi = \hat{H} \psi i ℏ ∂ t ∂ ψ = H ^ ψ
考虑某种不显含 t t t Q ^ \hat{Q} Q ^
ψ ′ = Q ^ ψ \psi' = \hat{Q} \psi ψ ′ = Q ^ ψ
体系对于变换的不变性 表现为 ψ \psi ψ ψ ′ \psi' ψ ′ 相同形式的运动方程 ,即要求 ψ ′ \psi' ψ ′
i ℏ ∂ ∂ t ψ ′ = H ^ ψ ′ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi' = \hat{H} \psi' i ℏ ∂ t ∂ ψ ′ = H ^ ψ ′
即
i ℏ ∂ ∂ t Q ^ ψ = H ^ Q ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \hat{Q}\psi = \hat{H} \hat{Q}\psi i ℏ ∂ t ∂ Q ^ ψ = H ^ Q ^ ψ
两边同时用 Q ^ − 1 \hat{Q}^{-1} Q ^ − 1
i ℏ ∂ ∂ t ψ = Q ^ − 1 H ^ Q ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi = \hat{Q}^{-1}\hat{H}\hat{Q} \psi i ℏ ∂ t ∂ ψ = Q ^ − 1 H ^ Q ^ ψ
与Schrödinger方程相比较,可知 Q ^ − 1 H ^ Q ^ = H ^ \hat{Q}^{-1}\hat{H}\hat{Q} = \hat{H} Q ^ − 1 H ^ Q ^ = H ^ H ^ Q ^ = Q ^ H ^ \hat{H}\hat{Q} = \hat{Q}\hat{H} H ^ Q ^ = Q ^ H ^
[ Q ^ , H ^ ] = 0 [ \hat{Q} , \hat{H} ] = 0 [ Q ^ , H ^ ] = 0
这就是体系(Hamilton量)在变换 Q ^ \hat{Q} Q ^ 不变性 的数学表达(若 Q ^ \hat{Q} Q ^ Q Q Q 对称性变换 。
考虑到概率守恒,即 ( ψ ′ , ψ ′ ) = ( ψ , ψ ) (\psi',\psi') = (\psi,\psi) ( ψ ′ , ψ ′ ) = ( ψ , ψ )
( ψ ′ , ψ ′ ) = ( Q ^ ψ , Q ^ ψ ) = ( ψ , Q ^ + Q ^ ψ ) (\psi',\psi') = (\hat{Q}\psi,\hat{Q}\psi) = (\psi,\hat{Q}^+\hat{Q}\psi) ( ψ ′ , ψ ′ ) = ( Q ^ ψ , Q ^ ψ ) = ( ψ , Q ^ + Q ^ ψ )
故 Q ^ \hat{Q} Q ^ 幺正算符 ,即
Q ^ + Q ^ = Q ^ + Q ^ = I ^ \hat{Q}^+\hat{Q} = \hat{Q}^+\hat{Q} = \hat{I} Q ^ + Q ^ = Q ^ + Q ^ = I ^
对于连续变换,可以考虑其为连续的无穷小变换,令
Q ^ = I ^ + i ε F ^ \hat{Q} = \hat{I} + \mathrm{i}\varepsilon\hat{F} Q ^ = I ^ + i ε F ^
其中 ε → 0 + \varepsilon \to 0^+ ε → 0 + Q Q Q
Q ^ + Q ^ = ( I ^ − i ε F ^ + ) ( I ^ + i ε F ^ ) = I ^ + i ε ( F ^ − F ^ + ) + O ( ε 2 ) = I ^ \hat{Q}^+\hat{Q} = \left( \hat{I} - \mathrm{i}\varepsilon\hat{F}^+ \right) \left( \hat{I} + \mathrm{i}\varepsilon\hat{F} \right) \ \ \ = \hat{I} + \mathrm{i}\varepsilon \left( \hat{F} - \hat{F}^+ \right) + O(\varepsilon^2) = \hat{I} Q ^ + Q ^ = ( I ^ − i ε F ^ + ) ( I ^ + i ε F ^ ) = I ^ + i ε ( F ^ − F ^ + ) + O ( ε 2 ) = I ^
即要求
F ^ = F ^ + \hat{F} = \hat{F}^+ F ^ = F ^ +
则 F ^ \hat{F} F ^ 厄米算符 ,称为变换 Q ^ \hat{Q} Q ^ 无穷小算符 (infinitesimal operator),由于其为厄米算符,可用它来定义一个与 Q ^ \hat{Q} Q ^ Q ^ \hat{Q} Q ^ [ Q ^ , H ^ ] = 0 [\hat{Q},\hat{H}] = 0 [ Q ^ , H ^ ] = 0
[ F ^ , H ^ ] = 0 [ \hat{F} , \hat{H} ] = 0 [ F ^ , H ^ ] = 0
由此可知 F F F 守恒量 。
此部分仅为注解。
更普遍来讲,如果一个变换不改变体系的各物理量的相互关系,则称为体系的一个对称性变换。
设体系的某一状态用 ψ \psi ψ ψ ′ \psi' ψ ′ ϕ \phi ϕ ϕ ′ \phi' ϕ ′
∣ ( ψ , ϕ ) ∣ = ∣ ( ψ ′ , ϕ ′ ) ∣ |(\psi,\phi)| = |(\psi',\phi')| ∣ ( ψ , ϕ ) ∣ = ∣ ( ψ ′ , ϕ ′ ) ∣
基于此要求,Winger指出:对称性变换只能是幺正变换或反幺正变换。对于连续变换,它们总可以从恒等变换出发,连续地经历无穷小变换来实现,这种变换只能是幺正变换。
一个体系若存在一个守恒量,则反映体系有某种对称性,反之,不一定成立。Winger还指出:对于幺正变换对称性,的确存在相应的守恒量,但对于反幺正变换对称性,如时间反演不变性,并不存在相应的守恒量。
这里使用一维的情形进行讨论,对应的坐标算符为 x ^ \hat{x} x ^ p ^ \hat{p} p ^
空间反射算符为 P ^ \hat{P} P ^
P ^ ψ ( x ) = ψ ( − x ) \hat{P} \psi(x) = \psi(-x) P ^ ψ ( x ) = ψ ( − x )
对算符 F ^ ( x ^ , p ^ ) \hat{F}(\hat{x},\hat{p}) F ^ ( x ^ , p ^ )
P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ ) \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ = \hat{F}(-\hat{x},-\hat{p}) P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ )
证明如下:
设算符 F ^ ( x ^ , p ^ ) \hat{F}(\hat{x},\hat{p}) F ^ ( x ^ , p ^ ) ψ ( x ) \psi(x) ψ ( x )
F ^ ( x ^ , p ^ ) ψ ( x ) = ϕ ( x ) \hat{F}(\hat{x},\hat{p}) \psi(x) = \phi(x) F ^ ( x ^ , p ^ ) ψ ( x ) = ϕ ( x )
做空间反射变换可得
P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ ϕ ( x ) \hat{P} \hat{F}(\hat{x},\hat{p}) \psi(x) = \hat{P} \phi(x) P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ ϕ ( x )
其中
P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = F ^ ( − x ^ , − p ^ ) ψ ( − x ) \hat{P} \hat{F}(\hat{x},\hat{p}) \psi(x) = \hat{F}(-\hat{x},-\hat{p}) \psi(-x) P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = F ^ ( − x ^ , − p ^ ) ψ ( − x )
已知 P ^ \hat{P} P ^
P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + P ^ ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + ψ ( − x ) \hat{P} \hat{F}(\hat{x},\hat{p}) \psi(x) = \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ \hat{P} \psi(x) = \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ \psi(-x) P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + P ^ ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + ψ ( − x )
两者对比有
P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ ) \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ = \hat{F}(-\hat{x},-\hat{p}) P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ )
如果Hamilton量空间反射不变,即
[ P ^ , H ^ ] = 0 [ \hat{P} , \hat{H} ] = 0 [ P ^ , H ^ ] = 0
则体系具有空间反射对称性 ,此时体系的宇称守恒 。
这里使用一维的情形进行讨论,对应的坐标算符为 x ^ \hat{x} x ^ p ^ \hat{p} p ^
考虑体系沿 x x x x → x ′ = x + δ x x \to x' = x + \delta x x → x ′ = x + δ x ψ \psi ψ
ψ ′ = D ^ ( δ x ) ψ \psi' = \hat{D}(\delta x) \psi ψ ′ = D ^ ( δ x ) ψ
无穷小平移变换 D ^ ( δ x ) \hat{D}(\delta x) D ^ ( δ x ) D ^ + ( δ x ) = D ^ − 1 ( δ x ) \hat{D}^+(\delta x) = \hat{D}^{-1}(\delta x) D ^ + ( δ x ) = D ^ − 1 ( δ x ) p ^ \hat{p} p ^
D ^ ( δ x ) = e − i ℏ δ x p ^ \hat{D}(\delta x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} D ^ ( δ x ) = e − ℏ i δ x p ^
证明如下:
对任意态 ψ \psi ψ ψ ′ \psi' ψ ′ x x x
∫ − ∞ + ∞ ψ ′ ∗ ( x ) x ψ ′ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x ) x ψ ( x ) d x + δ x = ∫ − ∞ + ∞ ψ ∗ ( x ) ( x + δ x ) ψ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x − δ x ) x ψ ( x − δ x ) d x \int_{-\infty}^{+\infty} \psi'^(x) x \psi'(x) \mathrm{d}x = \int_{-\infty}^{+\infty} \psi^ (x) x \psi(x) \mathrm{d}x + \delta x \ \ \ = \int_{-\infty}^{+\infty} \psi^(x) (x+\delta x) \psi(x) \mathrm{d}x \ \ \ = \int_{-\infty}^{+\infty} \psi^ (x-\delta x) x \psi(x-\delta x) \mathrm{d}x ∫ − ∞ + ∞ ψ ′ ∗ ( x ) x ψ ′ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x ) x ψ ( x ) d x + δ x = ∫ − ∞ + ∞ ψ ∗ ( x ) ( x + δ x ) ψ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x − δ x ) x ψ ( x − δ x ) d x
由此可知
ψ ′ ( x ) = ψ ( x − δ x ) \psi'(x) = \psi(x-\delta x) ψ ′ ( x ) = ψ ( x − δ x )
即 D ^ ( δ x ) ψ ( x ) = ψ ( x − δ x ) \hat{D}(\delta x) \psi(x) = \psi(x-\delta x) D ^ ( δ x ) ψ ( x ) = ψ ( x − δ x ) x x x
D ^ ( δ x ) ψ ( x ) = ∑ n = 0 + ∞ ( − δ x ) n n ! ∂ n ψ ( x ) ∂ x n = e − δ x ∂ ∂ x ψ ( x ) \hat{D}(\delta x) \psi(x) = \sum_{n=0}^{+\infty} \frac{(-\delta x)^n}{n!} \frac{\partial^n \psi(x)}{\partial x^n} = \mathrm{e}^{-\delta x \frac{\partial}{\partial x}} \psi(x) D ^ ( δ x ) ψ ( x ) = n = 0 ∑ + ∞ n ! ( − δ x ) n ∂ x n ∂ n ψ ( x ) = e − δ x ∂ x ∂ ψ ( x )
因为 ψ ( x ) \psi(x) ψ ( x ) p ^ = − i ℏ ∂ ∂ x \hat{p} = -\mathrm{i}\hbar \frac{\partial}{\partial x} p ^ = − i ℏ ∂ x ∂
D ^ ( δ x ) = e − i ℏ δ x p ^ \hat{D}(\delta x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} D ^ ( δ x ) = e − ℏ i δ x p ^
取厄米共轭可得
D ^ + ( δ x ) = ( e − i ℏ δ x p ^ ) + = [ ∑ n = 0 + ∞ 1 n ! ( − i ℏ δ x ) n p ^ n ] + = ∑ n = 0 + ∞ 1 n ! ( i ℏ δ x ) n p ^ n = e i ℏ δ x p ^ = D ^ − 1 ( δ x ) \hat{D}^+(\delta x) = \left( \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} \right)^+ \ \ \ = \left[ \sum_{n=0}^{+\infty} \frac{1}{n!} ( -\frac{\mathrm{i}}{\hbar}\delta x )^n \hat{p}^n \right]^+ \ \ \ = \sum_{n=0}^{+\infty} \frac{1}{n!} ( \frac{\mathrm{i}}{\hbar}\delta x )^n \hat{p}^n \ \ \ = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} \ \ \ = \hat{D}^{-1}(\delta x) D ^ + ( δ x ) = ( e − ℏ i δ x p ^ ) + = [ n = 0 ∑ + ∞ n ! 1 ( − ℏ i δ x ) n p ^ n ] + = n = 0 ∑ + ∞ n ! 1 ( ℏ i δ x ) n p ^ n = e ℏ i δ x p ^ = D ^ − 1 ( δ x )
即 D ^ ( δ x ) \hat{D}(\delta x) D ^ ( δ x )
D ^ ( δ x ) ψ ( x ) = e − i ℏ δ x p ^ ψ ( x ) = ψ ( x − δ x ) \hat{D}(\delta x) \psi(x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}}\psi(x) = \psi(x-\delta x) D ^ ( δ x ) ψ ( x ) = e − ℏ i δ x p ^ ψ ( x ) = ψ ( x − δ x )
D ^ ( δ x ) F ^ D ^ + ( δ x ) = e − i ℏ δ x p ^ F ^ e i ℏ δ x p ^ \hat{D}(\delta x)\hat{F}\hat{D}^+(\delta x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} \hat{F} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} D ^ ( δ x ) F ^ D ^ + ( δ x ) = e − ℏ i δ x p ^ F ^ e ℏ i δ x p ^
如果Hamilton量空间平移不变,即
[ D ^ , H ^ ] = 0 [ \hat{D} , \hat{H} ] = 0 [ D ^ , H ^ ] = 0
则体系具有空间平移对称性 ,此时体系的动量守恒 。
这是因为
[ D ^ , H ^ ] = 0 ⇓ [ ∑ n = 0 + ∞ 1 n ! ( − i ℏ δ x ) n p ^ n , H ^ ] = 0 ⇓ ∑ n = 0 + ∞ 1 n ! ( − i ℏ δ x ) n [ p ^ n , H ^ ] = 0 ⇓ [ p ^ , H ^ ] = 0 \ [ \hat{D} , \hat{H} ] = 0 \ \Downarrow \ \ [ \sum_{n=0}^{+\infty} \frac{1}{n!} ( -\frac{\mathrm{i}}{\hbar}\delta x )^n \hat{p}^n , \hat{H} ] = 0 \ \Downarrow \ \ \sum_{n=0}^{+\infty} \frac{1}{n!} ( -\frac{\mathrm{i}}{\hbar}\delta x )^n [ \hat{p}^n , \hat{H} ] = 0 \ \Downarrow \ \ [ \hat{p} , \hat{H} ] = 0 [ D ^ , H ^ ] = 0 ⇓ [ n = 0 ∑ + ∞ n ! 1 ( − ℏ i δ x ) n p ^ n , H ^ ] = 0 ⇓ n = 0 ∑ + ∞ n ! 1 ( − ℏ i δ x ) n [ p ^ n , H ^ ] = 0 ⇓ [ p ^ , H ^ ] = 0
考虑体系绕 n ⃗ \vec{n}, n φ → φ ′ = φ + δ φ \varphi \to \varphi' = \varphi + \delta \varphi φ → φ ′ = φ + δ φ ψ \psi ψ
ψ ′ = R ^ ( δ φ n ⃗ ) ψ \psi' = \hat{R}(\delta \varphi\ \vec{n}) \psi ψ ′ = R ^ ( δ φ n ) ψ
无穷小转动变换 R ^ ( δ φ n ⃗ ) \hat{R}(\delta \varphi\ \vec{n}) R ^ ( δ φ n ) R ^ + ( δ φ n ⃗ ) = R ^ − 1 ( δ φ n ⃗ ) \hat{R}^+(\delta \varphi\ \vec{n}) = \hat{R}^{-1}(\delta \varphi\ \vec{n}) R ^ + ( δ φ n ) = R ^ − 1 ( δ φ n ) L ^ \hat{L} L ^
R ^ ( δ φ n ⃗ ) = e − i ℏ δ φ n ⃗ ⋅ L ⃗ ^ \hat{R}(\delta \varphi\ \vec{n}) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi\ \vec{n} \cdot \hat{\vec{L}}} R ^ ( δ φ n ) = e − ℏ i δ φ n ⋅ L ^
如果 n ⃗ \vec{n}, n z z z
R ^ ( δ φ ) = e − i ℏ δ φ L ^ z \hat{R}(\delta \varphi) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} R ^ ( δ φ ) = e − ℏ i δ φ L ^ z
以 n ⃗ \vec{n}, n z z z
R ^ ( δ φ ) ψ ( φ ) = e − i ℏ δ φ L ^ z ψ ( φ ) = ψ ( φ − δ φ ) \hat{R}(\delta \varphi) \psi(\varphi) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} \psi(\varphi) = \psi(\varphi-\delta \varphi) R ^ ( δ φ ) ψ ( φ ) = e − ℏ i δ φ L ^ z ψ ( φ ) = ψ ( φ − δ φ )
R ^ ( δ φ ) F ^ ( φ ) R ^ + ( δ φ ) = e − i ℏ δ φ L ^ z F ^ ( φ ) e i ℏ δ φ L ^ z \hat{R}(\delta \varphi) \hat{F}(\varphi) \hat{R}^+(\delta \varphi) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} \hat{F}(\varphi) \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} R ^ ( δ φ ) F ^ ( φ ) R ^ + ( δ φ ) = e − ℏ i δ φ L ^ z F ^ ( φ ) e ℏ i δ φ L ^ z
如果Hamilton量空间转动不变,即
[ R ^ , H ^ ] = 0 [ \hat{R} , \hat{H} ] = 0 [ R ^ , H ^ ] = 0
则体系具有空间转动对称性 ,此时体系的角动量守恒 ,即
[ L ⃗ ^ , H ^ ] = 0 [ \hat{\vec{L}} , \hat{H} ] = 0 [ L ^ , H ^ ] = 0
考虑将时间停滞一段 τ \tau τ
D ^ ( τ ) ψ ( t ) = ψ ( t + τ ) \hat{D}(\tau) \psi(t) = \psi(t+\tau) D ^ ( τ ) ψ ( t ) = ψ ( t + τ )
这称为时间平移变换 (属于连续变换),算符
D ^ ( τ ) = e τ ∂ ∂ t \hat{D}(\tau) = \mathrm{e}^{\tau \frac{\partial}{\partial t}} D ^ ( τ ) = e τ ∂ t ∂
如果Hamilton量时间平移不变,即
D ^ ( τ ) H ^ D ^ + ( τ ) = H ^ \hat{D}(\tau) \hat{H} \hat{D}^+(\tau) = \hat{H} D ^ ( τ ) H ^ D ^ + ( τ ) = H ^
此即 [ D ^ ( τ ) , H ^ ] = 0 [\hat{D}(\tau) , \hat{H}] = 0 [ D ^ ( τ ) , H ^ ] = 0 能量守恒 。证明如下:
[ D ^ ( τ ) , H ^ ] = 0 ⇓ [ e τ ∂ ∂ t , H ^ ] = 0 ⇓ [ ∑ n = 0 + ∞ τ n n ! ∂ n ∂ t n , H ^ ] = 0 ⇓ ∑ n = 0 + ∞ τ n n ! [ ∂ n ∂ t n , H ^ ] = 0 ⇓ [ ∂ ∂ t , H ^ ] = 0 ⇓ [ ∂ ∂ t , H ^ ] ψ = ∂ ∂ t ( H ^ ψ ) − H ^ ∂ ∂ t ψ = ψ ∂ H ^ ∂ t = 0 ⇓ ∂ H ^ ∂ t = 0 \left[ \hat{D}(\tau) , \hat{H} \right] = 0 \ \Downarrow \ \left[ \mathrm{e}^{\tau \frac{\partial}{\partial t}} , \hat{H} \right] = 0 \ \Downarrow \ \left[ \sum_{n=0}^{+\infty} \frac{\tau^n}{n!} \frac{\partial^n}{\partial t^n} , \hat{H} \right] = 0 \ \Downarrow \ \sum_{n=0}^{+\infty} \frac{\tau^n}{n!} \left[ \frac{\partial^n}{\partial t^n} , \hat{H} \right] = 0 \ \Downarrow \ \left[ \frac{\partial}{\partial t} , \hat{H} \right] = 0 \ \Downarrow \ \left[ \frac{\partial}{\partial t} , \hat{H} \right] \psi = \frac{\partial}{\partial t} (\hat{H} \psi) - \hat{H} \frac{\partial}{\partial t} \psi = \psi \frac{\partial \hat{H}}{\partial t} = 0 \ \Downarrow \ \frac{\partial \hat{H}}{\partial t} = 0 [ D ^ ( τ ) , H ^ ] = 0 ⇓ [ e τ ∂ t ∂ , H ^ ] = 0 ⇓ [ n = 0 ∑ + ∞ n ! τ n ∂ t n ∂ n , H ^ ] = 0 ⇓ n = 0 ∑ + ∞ n ! τ n [ ∂ t n ∂ n , H ^ ] = 0 ⇓ [ ∂ t ∂ , H ^ ] = 0 ⇓ [ ∂ t ∂ , H ^ ] ψ = ∂ t ∂ ( H ^ ψ ) − H ^ ∂ t ∂ ψ = ψ ∂ t ∂ H ^ = 0 ⇓ ∂ t ∂ H ^ = 0
此时可以证明时间平移变换可以表示为
D ^ ( τ ) = e − i ℏ τ H ^ \hat{D}(\tau) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \tau \hat{H}} D ^ ( τ ) = e − ℏ i τ H ^
即与时间平移变换相联系的力学量是能量。证明如下
根据Schrödinger方程
i ℏ ∂ ∂ t ψ = H ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi = \hat{H} \psi i ℏ ∂ t ∂ ψ = H ^ ψ
可知
∂ ∂ t ψ = 1 i ℏ H ^ ψ \frac{\partial}{\partial t} \psi = \frac{1}{\mathrm{i}\hbar} \hat{H} \psi ∂ t ∂ ψ = i ℏ 1 H ^ ψ
归纳可得
∂ n ∂ t n ψ = ( 1 i ℏ H ^ ) n ψ \frac{\partial^n}{\partial t^n} \psi = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^n \psi ∂ t n ∂ n ψ = ( i ℏ 1 H ^ ) n ψ
这是因为在已知对 n − 1 n-1 n − 1
∂ n ∂ t n ψ = ∂ ∂ t [ ( 1 i ℏ H ^ ) n − 1 ψ ] = ( 1 i ℏ H ^ ) n − 1 ∂ ψ ∂ t + ψ ∂ ∂ t ( 1 i ℏ H ^ ) n − 1 = ( 1 i ℏ H ^ ) n − 1 1 i ℏ H ^ ψ + ψ ( 1 i ℏ ) n − 1 ( n − 1 ) H ^ n − 2 ∂ H ^ ∂ t = ( 1 i ℏ H ^ ) n ψ \frac{\partial^n}{\partial t^n} \psi = \frac{\partial}{\partial t} \left[ \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \psi \right] \ \ \ = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \frac{\partial \psi}{\partial t} + \psi \frac{\partial}{\partial t} \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \ \ \ = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \frac{1}{\mathrm{i}\hbar} \hat{H} \psi + \psi \left( \frac{1}{\mathrm{i}\hbar}\right)^{n-1} (n-1) \hat{H}^{n-2} \frac{\partial \hat{H}}{\partial t} \ \ \ = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^n \psi ∂ t n ∂ n ψ = ∂ t ∂ [ ( i ℏ 1 H ^ ) n − 1 ψ ] = ( i ℏ 1 H ^ ) n − 1 ∂ t ∂ ψ + ψ ∂ t ∂ ( i ℏ 1 H ^ ) n − 1 = ( i ℏ 1 H ^ ) n − 1 i ℏ 1 H ^ ψ + ψ ( i ℏ 1 ) n − 1 ( n − 1 ) H ^ n − 2 ∂ t ∂ H ^ = ( i ℏ 1 H ^ ) n ψ
在量子力学中,把属于同一类的粒子成为全同 (identical)粒子 ,它们具有完全相同的内禀属性,包括静质量、电荷、自旋、磁矩、寿命等。
量子力学中,由于态的量子化 ,两个量子态要么完全相同,要么完全不同,中间无连续过度,因此与经典力学的连续变化不同,具有全同粒子的问题。
当两个全同粒子的波函数在空间中发生重叠的时候,我们无法区分哪个是“第一个”粒子,哪个是“第二个”粒子。所以全同粒子是不可分辨 的,即不能“标记”、“跟踪”,此时经典统计被量子统计取代。
全部量子力学实验表明,如果让两个全同粒子处于相同的物理条件下,它们将有完全相同的实验表现,故从原理上 (永远的、非技术性的)看将无法区分它们谁是谁。
全同粒子体系中任意两个全同粒子的交换,都不改变体系的物理状态,即所处的量子态是不变的,故可观测量(尤其是Hamilton量)是不变的。
考虑 N N N ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) q i ( i = 1 , 2 , ⋯ , N ) q_i\ (i=1,2,\cdots,N) q i ( i = 1 , 2 , ⋯ , N ) 交换算符 P ^ i j \hat{P}_{ij} P ^ ij i i i j j j
P ^ i j ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) = ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) \hat{P}_{ij} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) = \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) P ^ ij ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) = ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N )
而根据全同性假设, ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N )
P ^ i j ψ = C ψ ⇓ P ^ i j 2 ψ = C 2 ψ = ψ ⇓ C 2 = 1 ⇓ C = ± 1 \hat{P}{ij} \psi = C \psi \ \Downarrow \ \hat{P} {ij}^2 \psi = C^2 \psi = \psi \ \Downarrow \ C^2 = 1 \ \Downarrow \ C = \pm 1 P ^ ij ψ = C ψ ⇓ P ^ ij 2 ψ = C 2 ψ = ψ ⇓ C 2 = 1 ⇓ C = ± 1
即 P ^ i j \hat{P}_{ij} P ^ ij C = ± 1 C = \pm 1 C = ± 1
P ^ i j ψ = { + ψ , 交换对称波函数 − ψ , 交换反对称波函数 \hat{P}_{ij} \psi = \begin{cases} + \psi & ,交换对称波函数 \ - \psi & ,交换反对称波函数 \ \end{cases} P ^ ij ψ = { + ψ − ψ , 交换对称波函数 , 交换反对称波函数
所以全同粒子体系的全同性假设给了波函数一个很强的限制,即要求它们对于任意两个粒子交换,或者对称 (symmetric),或者反对称 (anti-symmetrix)。
注:交换算符是厄米算符、幺正算符,这是因为:
∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) P ^ i j ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) d τ = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ( 令 d τ ′ = d q 1 ⋯ d q j ⋯ d q i ⋯ d q N = d τ ) = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ = ∫ ( 全 ) [ P ^ i j ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) ] ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ ⇓ P ^ i j + = P ^ i j \int_{(全)} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \hat{P}{ij} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \mathrm{d}\tau \ \ \ = \int {(全)} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \mathrm{d}\tau \ \ \ (令 \mathrm{d}\tau' = \mathrm{d}q_1\cdots\mathrm{d}q_j\cdots\mathrm{d}q_i\cdots\mathrm{d}q_N = \mathrm{d}\tau) \ \ \ = \int_{(全)} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \mathrm{d}\tau' \ \ \ = \int_{(全)} \left[ \hat{P}{ij}\psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \right] \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \mathrm{d}\tau' \ \Downarrow \ \hat{P} {ij}^+ = \hat{P}_{ij} ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) P ^ ij ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) d τ = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ( 令 d τ ′ = d q 1 ⋯ d q j ⋯ d q i ⋯ d q N = d τ ) = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ = ∫ ( 全 ) [ P ^ ij ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) ] ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ ⇓ P ^ ij + = P ^ ij
P ^ i j P ^ i j = I ^ ⟹ P ^ i j = P ^ i j − 1 ⟹ P ^ i j + = P ^ i j − 1 \hat{P}{ij}\hat{P} {ij} = \hat{I} \Longrightarrow \hat{P}{ij} = \hat{P} {ij}^{-1} \Longrightarrow \hat{P}{ij}^+ = \hat{P} {ij}^{-1} P ^ ij P ^ ij = I ^ ⟹ P ^ ij = P ^ ij − 1 ⟹ P ^ ij + = P ^ ij − 1
对于全同粒子体系,
[ P ^ i j , H ^ ] = 0 ( i ≠ j = 1 , 2 , 3 , ⋯ , N ) [\hat{P}_{ij} , \hat{H}] = 0 \kern 2em (i \ne j = 1,2,3,\cdots,N) [ P ^ ij , H ^ ] = 0 ( i = j = 1 , 2 , 3 , ⋯ , N )
即所有的 P ^ i j \hat{P}_{ij} P ^ ij
P ^ i j H ^ P ^ i j + = H ^ \hat{P}{ij} \hat{H} \hat{P} {ij}^+ = \hat{H} P ^ ij H ^ P ^ ij + = H ^
证明如下:
记 ( q i , q j ) = ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) (q_i,q_j) = (q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ( q i , q j ) = ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N )
H ^ ( q i , q j ) ψ ( q i , q j ) = E ψ ( q i , q j ) \hat{H} (q_i,q_j) \psi(q_i,q_j) = E \psi(q_i,q_j) H ^ ( q i , q j ) ψ ( q i , q j ) = E ψ ( q i , q j )
两边同时用 P ^ i j \hat{P}_{ij} P ^ ij
P ^ i j [ H ^ ( q i , q j ) ψ ( q i , q j ) ] = P ^ i j [ E ψ ( q i , q j ) ] ⇓ H ^ ( q j , q i ) ψ ( q j , q i ) = E ψ ( q j , q i ) \hat{P}{ij} \left[ \hat{H} (q_i,q_j) \psi(q_i,q_j) \right] = \hat{P} {ij} \left[ E \psi(q_i,q_j) \right] \ \Downarrow \ \hat{H} (q_j,q_i) \psi(q_j,q_i) = E \psi(q_j,q_i) P ^ ij [ H ^ ( q i , q j ) ψ ( q i , q j ) ] = P ^ ij [ E ψ ( q i , q j ) ] ⇓ H ^ ( q j , q i ) ψ ( q j , q i ) = E ψ ( q j , q i )
考虑到波函数的交换对称性,即 ψ ( q j , q i ) = C ψ ( q i , q j ) \psi(q_j,q_i) = C \psi(q_i,q_j) ψ ( q j , q i ) = C ψ ( q i , q j )
H ^ ( q j , q i ) C ψ ( q i , q j ) = E C ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) ψ ( q i , q j ) = E ψ ( q i , q j ) = H ^ ( q i , q j ) ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) = H ^ ( q i , q j ) ⇓ P ^ i j H ^ ( q i , q j ) P ^ i j + = H ^ ( q i , q j ) ⇓ [ P ^ i j , H ^ ] = 0 \hat{H} (q_j,q_i) C \psi(q_i,q_j) = E C \psi(q_i,q_j) \ \Downarrow \ \hat{H} (q_j,q_i) \psi(q_i,q_j) = E \psi(q_i,q_j) = \hat{H} (q_i,q_j) \psi(q_i,q_j) \ \Downarrow \ \hat{H} (q_j,q_i) = \hat{H} (q_i,q_j) \ \Downarrow \ \hat{P}{ij} \hat{H} (q_i,q_j) \hat{P} {ij}^+ = \hat{H} (q_i,q_j) \ \Downarrow \ \ [\hat{P}_{ij} , \hat{H}] = 0 H ^ ( q j , q i ) C ψ ( q i , q j ) = EC ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) ψ ( q i , q j ) = E ψ ( q i , q j ) = H ^ ( q i , q j ) ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) = H ^ ( q i , q j ) ⇓ P ^ ij H ^ ( q i , q j ) P ^ ij + = H ^ ( q i , q j ) ⇓ [ P ^ ij , H ^ ] = 0
凡自旋为 ℏ \hbar ℏ 整数倍 ( s = 0 , 1 , 2 , ⋯ ) (s=0,1,2,\cdots) ( s = 0 , 1 , 2 , ⋯ ) 对称 的,如 π \pi π ( s = 0 ) (s=0) ( s = 0 ) ( s = 1 ) (s=1) ( s = 1 ) Bose-Einstein统计 ,故称为Bose子 。
凡自旋为 ℏ \hbar ℏ 半整数倍 ( s = 1 2 , 3 2 , ⋯ ) (s=\frac12,\frac32,\cdots) ( s = 2 1 , 2 3 , ⋯ ) 反对称 的,如电子、质子、中子 ( 均 s = 1 2 ) (均s=\frac12) ( 均 s = 2 1 ) Fermi-Dirac统计 ,故称为Fermi子 。
由基本粒子所组成的复合粒子,若在讨论的问题或过程中其内部状态保持不变,即内部自由度完全被冻结,则全同性概念仍然使用,也可以当成一类全同粒子来处理,其统计性质按如下规则确定:
若复合粒子由Bose子组成,则为Bose子;
若复合粒子由偶数个Fermi子组成,则为Bose子;
若复合粒子由奇数个Fermi子组成,则为Fermi子。
若 ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N )
由上述定理可得:把全同粒子体系的波函数和其交换项进行叠加,叠加后的波函数仍满足Schrödinger方程, 这是我们能够将波函数对称化或反对称化的理论依据。
一般地说,一个全同粒子体系的波函数是解Schrödinger方程得到的,但未必有确定的交换对称性,而交换算符与Hamilton量的共同本征函数是完全对称波函数或完全反对称波函数,所以我们要对解得的波函数进行“对称化 ”或“反对称化 ”。
忽略全同粒子体系中各粒子之间的相互作用,可以将其视为无耦合体系,此时体系的总波函数是各个粒子波函数的乘积,Hamilton量是各个粒子Hamilton量的和
Ψ ( q 1 , q 2 ⋯ , q N ) = ψ 1 ( q 1 ) ψ 2 ( q 2 ) ⋯ ψ N ( q N ) \Psi(q_1,q_2\cdots,q_N) = \psi_1(q_1) \psi_2(q_2) \cdots \psi_N(q_N) Ψ ( q 1 , q 2 ⋯ , q N ) = ψ 1 ( q 1 ) ψ 2 ( q 2 ) ⋯ ψ N ( q N )
H ^ = ∑ i H ^ i \hat{H} = \sum_i \hat{H}_i H ^ = i ∑ H ^ i
二粒子体系进行单粒子近似后得到的波函数为
Ψ ( q 1 , q 2 ) = ψ 1 ( q 1 ) ψ 2 ( q 2 ) \Psi(q_1,q_2) = \psi_1(q_1) \psi_2(q_2) Ψ ( q 1 , q 2 ) = ψ 1 ( q 1 ) ψ 2 ( q 2 )
进行对称化 后,归一化的波函数为
Ψ S ( q 1 , q 2 ) = 1 2 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) + ψ 1 ( q 2 ) ψ 2 ( q 1 ) ] \Psi^S(q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_1(q_1)\psi_2(q_2) + \psi_1(q_2)\psi_2(q_1) \right] Ψ S ( q 1 , q 2 ) = 2 1 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) + ψ 1 ( q 2 ) ψ 2 ( q 1 ) ]
进行反对称化 后,归一化的波函数为
Ψ A ( q 1 , q 2 ) = 1 2 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) − ψ 1 ( q 2 ) ψ 2 ( q 1 ) ] \Psi^A(q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_1(q_1)\psi_2(q_2) - \psi_1(q_2)\psi_2(q_1) \right] Ψ A ( q 1 , q 2 ) = 2 1 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) − ψ 1 ( q 2 ) ψ 2 ( q 1 ) ]
对于两个全同Bose子 组成的体系,应该满足交换对称 ,即
P ^ 12 Ψ k 1 k 2 S ( q 1 , q 2 ) = Ψ k 1 k 2 S ( q 1 , q 2 ) \hat{P}{12} \Psi^S {k_1k_2} (q_1,q_2) = \Psi^S_{k_1k_2} (q_1,q_2) P ^ 12 Ψ k 1 k 2 S ( q 1 , q 2 ) = Ψ k 1 k 2 S ( q 1 , q 2 )
当 k 1 ≠ k 2 k_1 \ne k_2 k 1 = k 2
Ψ k 1 k 2 S ( q 1 , q 2 ) = 1 2 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) + ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 1 2 ( 1 + P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) \Psi^S_{k_1k_2} (q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_{k_1}(q_1)\psi_{k_2}(q_2) + \psi_{k_1}(q_2)\psi_{k_2}(q_1) \right] \ \ \ = \frac{1}{\sqrt{2}} \left( 1 + \hat{P}{12} \right) \psi {k_1}(q_1)\psi_{k_2}(q_2) Ψ k 1 k 2 S ( q 1 , q 2 ) = 2 1 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) + ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 2 1 ( 1 + P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 )
当 k 1 = k 2 = k k_1 = k_2 = k k 1 = k 2 = k
Ψ k k S ( q 1 , q 2 ) = ψ k ( q 1 ) ψ k ( q 2 ) \Psi^S_{kk} (q_1,q_2) = \psi_{k}(q_1)\psi_{k}(q_2) Ψ kk S ( q 1 , q 2 ) = ψ k ( q 1 ) ψ k ( q 2 )
该波函数不恒为零表明在一个粒子态上可以存在多个Bose子。
对于两个全同Fermi子 组成的体系,应该满足交换反对称 ,即
P ^ 12 Ψ k 1 k 2 A ( q 1 , q 2 ) = − Ψ k 1 k 2 A ( q 1 , q 2 ) \hat{P}{12} \Psi^A {k_1k_2} (q_1,q_2) = - \Psi^A_{k_1k_2} (q_1,q_2) P ^ 12 Ψ k 1 k 2 A ( q 1 , q 2 ) = − Ψ k 1 k 2 A ( q 1 , q 2 )
当 k 1 ≠ k 2 k_1 \ne k_2 k 1 = k 2
Ψ k 1 k 2 A ( q 1 , q 2 ) = 1 2 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) − ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 1 2 ∣ ψ k 1 ( q 1 ) ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ψ k 2 ( q 2 ) ∣ = 1 2 ( 1 − P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) \Psi^A_{k_1k_2} (q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_{k_1}(q_1)\psi_{k_2}(q_2) - \psi_{k_1}(q_2)\psi_{k_2}(q_1) \right] \ \ \ = \frac{1}{\sqrt{2}} \begin{vmatrix} \psi_{k_1}(q_1) & \psi_{k_1}(q_2) \ \psi_{k_2}(q_1) & \psi_{k_2}(q_2) \end{vmatrix} \ \ \ = \frac{1}{\sqrt{2}} \left( 1 - \hat{P}{12} \right) \psi {k_1}(q_1)\psi_{k_2}(q_2) Ψ k 1 k 2 A ( q 1 , q 2 ) = 2 1 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) − ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 2 1 ψ k 1 ( q 1 ) ψ k 2 ( q 1 ) ψ k 1 ( q 2 ) ψ k 2 ( q 2 ) = 2 1 ( 1 − P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 )
当 k 1 = k 2 = k k_1 = k_2 = k k 1 = k 2 = k Ψ k k A ( q 1 q 2 ) ≡ 0 \Psi^A_{kk}(q_1q_2) \equiv 0 Ψ kk A ( q 1 q 2 ) ≡ 0 Pauli不相容原理 。
由于Bose子不受Pauli不相容原理的限制,可以有多个Bose子处在同一量子态上,故设有 N N N M M M M ≤ N M \le N M ≤ N n i n_i n i k i k_i k i i = 0 , 1 , ⋯ , M i=0,1,\cdots,M i = 0 , 1 , ⋯ , M ∑ i = 1 M n i = N \sum_{i=1}^{M} n_i = N ∑ i = 1 M n i = N
Ψ k 1 ⋯ k M S ( q 1 , ⋯ , q N ) = ∏ i = 1 M n i ! N ! ∑ P ^ P ^ ∏ i = 1 M ∏ j = 1 n i ψ k i ( q N i − 1 + j ) \Psi^{S}{k_1 \cdots k_M} (q_1,\cdots,q_N) = \sqrt{\frac{\prod {i=1}^{M}n_i!}{N!}} \sum_{\hat{P}} \hat{P} \prod_{i=1}^{M} \prod_{j=1}^{n_i} \psi_{k_i}(q_{N_{i-1}+j}) Ψ k 1 ⋯ k M S ( q 1 , ⋯ , q N ) = N ! ∏ i = 1 M n i ! P ^ ∑ P ^ i = 1 ∏ M j = 1 ∏ n i ψ k i ( q N i − 1 + j )
式中 Ψ S \Psi^S Ψ S k i k_i k i n i n_i n i N i = ∑ l = 1 i n l N_i = \sum_{l=1}^{i} n_l N i = ∑ l = 1 i n l i i i P ^ \hat{P} P ^ 这样其个数就与组合数而非排列数相关 ),这样的置换共有
∏ i = 1 M C N i n i = ∏ i = 1 M N i ! ( N i − n i ) ! n i ! = ∏ i = 1 M N i ! N i − 1 ! n i ! = N ! ∏ i = 1 M 1 n i ! \prod_{i=1}^{M} C^{n_i}{N_i} = \prod {i=1}^{M} \frac{N_i!}{(N_i-n_i)!\ n_i!} = \prod_{i=1}^{M} \frac{N_i!}{N_{i-1}!\ n_i!} = N! \prod_{i=1}^{M} \frac{1}{n_i!} i = 1 ∏ M C N i n i = i = 1 ∏ M ( N i − n i )! n i ! N i ! = i = 1 ∏ M N i − 1 ! n i ! N i ! = N ! i = 1 ∏ M n i ! 1
个,此亦即归一化系数的来源。
这里采用的分析方法是对全同粒子进行人为编号, 写出波函数的每一项, 然后把它们适当线性叠加, 进而构造满足交换对称性要求的波函数。但实际上这一编号没有意义,更简单的做法是使用二次量子化(second quantization)方法,即粒子填布数(occupation number)表象,用单粒子态上的粒子占有数表示, ∣ n 1 n 2 ⋯ n M ⟩ = ∣ n 1 ⟩ ∣ n 2 ⟩ ⋯ ∣ n M ⟩ | n_1n_2 \cdots n_M \rangle = | n_1 \rangle | n_2 \rangle \cdots | n_M \rangle ∣ n 1 n 2 ⋯ n M ⟩ = ∣ n 1 ⟩ ∣ n 2 ⟩ ⋯ ∣ n M ⟩ ψ 1 , ψ 2 , ⋯ , ψ M \psi_1,\psi_2,\cdots,\psi_M ψ 1 , ψ 2 , ⋯ , ψ M n 1 , n 2 , ⋯ , n M n_1,n_2,\cdots,n_M n 1 , n 2 , ⋯ , n M n 1 n 2 ⋯ n M n_1n_2 \cdots n_M n 1 n 2 ⋯ n M Ψ S \Psi^S Ψ S
由于Fermi子受Pauli不相容原理的限制,一个量子态上只能有一个Fermi子,故设 N N N k 1 , k 2 , ⋯ , k N k_1,k_2,\cdots,k_N k 1 , k 2 , ⋯ , k N
Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = 1 N ! ∣ ψ k 1 ( q 1 ) ψ k 1 ( q 2 ) ⋯ ψ k 1 ( q N ) ψ k 2 ( q 1 ) ψ k 2 ( q 2 ) ⋯ ψ k 2 ( q N ) ⋮ ⋮ ⋱ ⋮ ψ k N ( q 1 ) ψ k N ( q 2 ) ⋯ ψ k N ( q N ) ∣ \Psi^A_{k_1k_2 \cdots k_N} (q_1,q_2,\cdots,q_N) = \frac{1}{\sqrt{N!}} \begin{vmatrix} \psi_{k_1}(q_1) & \psi_{k_1}(q_2) & \cdots & \psi_{k_1}(q_N) \ \psi_{k_2}(q_1) & \psi_{k_2}(q_2) & \cdots & \psi_{k_2}(q_N) \ \vdots & \vdots & \ddots & \vdots \ \psi_{k_N}(q_1) & \psi_{k_N}(q_2) & \cdots & \psi_{k_N}(q_N) \ \end{vmatrix} Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = N ! 1 ψ k 1 ( q 1 ) ψ k 2 ( q 1 ) ⋮ ψ k N ( q 1 ) ψ k 1 ( q 2 ) ψ k 2 ( q 2 ) ⋮ ψ k N ( q 2 ) ⋯ ⋯ ⋱ ⋯ ψ k 1 ( q N ) ψ k 2 ( q N ) ⋮ ψ k N ( q N )
此式称为Slater行列式 ,也可以表示为
Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = A ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) ⋯ ψ k N ( q N ) \Psi^A_{k_1k_2 \cdots k_N} (q_1,q_2,\cdots,q_N) = \mathcal{A} \psi_{k_1}(q_1) \psi_{k_2}(q_2) \cdots \psi_{k_N}(q_N) Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = A ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) ⋯ ψ k N ( q N )
其中反对称算符
A = 1 N ! ∑ P ^ δ P ^ P ^ \mathcal{A} = \frac{1}{\sqrt{N!}} \sum_{\hat{P}} \delta_{\hat{P}} \hat{P} A = N ! 1 P ^ ∑ δ P ^ P ^
式中的 P ^ \hat{P} P ^ N ! N! N ! I ^ \hat{I} I ^ δ P ^ = − 1 \delta_{\hat{P}} = -1 δ P ^ = − 1 δ P ^ = 1 \delta_{\hat{P}} = 1 δ P ^ = 1
中心力场中的问题常使用球坐标系 ( r , θ , φ ) (r,\theta,\varphi) ( r , θ , φ ) V V V r r r θ , φ \theta,\varphi θ , φ
H ^ = p ⃗ ^ 2 2 μ + V ( r ) \hat{H} = \frac{\hat{\vec{p}}^2}{2\mu} + V(r) H ^ = 2 μ p ^ 2 + V ( r )
直接考虑角动量 L ⃗ ^ \hat{\vec{L}} L ^
d d t L ⃗ ^ = d d t ( r ⃗ ^ × p ⃗ ^ ) = d r ⃗ ^ d t × p ⃗ ^ + r ⃗ ^ × d p ⃗ ^ d t = p ⃗ ^ μ × p ⃗ ^ + r ⃗ ^ × [ − ∇ V ( r ) ] = 0 − r ⃗ ^ × e ⃗ r d V ( r ) d r = 0 \frac{\mathrm{d}}{\mathrm{d}t} \hat{\vec{L}} = \frac{\mathrm{d}}{\mathrm{d}t} (\hat{\vec{r}} \times \hat{\vec{p}}) \ \ \ = \frac{\mathrm{d}\hat{\vec{r}}}{\mathrm{d}t} \times \hat{\vec{p}} + \hat{\vec{r}} \times \frac{\mathrm{d}\hat{\vec{p}}}{\mathrm{d}t} \ \ \ = \frac{\hat{\vec{p}}}{\mu} \times \hat{\vec{p}} + \hat{\vec{r}} \times [-\nabla V(r)] \ \ \ = 0 - \hat{\vec{r}} \times \vec{e}_r \frac{\mathrm{d}V(r)}{\mathrm{d}r} \ \ \ = 0 d t d L ^ = d t d ( r ^ × p ^ ) = d t d r ^ × p ^ + r ^ × d t d p ^ = μ p ^ × p ^ + r ^ × [ − ∇ V ( r )] = 0 − r ^ × e r d r d V ( r ) = 0
故角动量守恒 。同时根据 L ⃗ ⋅ r ⃗ = L ⃗ ⋅ p ⃗ = 0 \vec{L} \cdot \vec{r} = \vec{L} \cdot \vec{p} = 0 L ⋅ r = L ⋅ p = 0 L ⃗ \vec{L} L r ⃗ \vec{r}, r p ⃗ \vec{p}, p L ⃗ \vec{L} L 平面运动 ,平面的法向即为 L ⃗ \vec{L} L
也可以直接从对易关系来证明角动量守恒:
根据 [ L α , p β ] = ε α β γ i ℏ p γ [L_{\alpha} , p_{\beta}] = \varepsilon_{\alpha\beta\gamma} \mathrm{i} \hbar p_{\gamma} [ L α , p β ] = ε α β γ i ℏ p γ [ p α , p β ] = 0 [p_{\alpha},p_{\beta}] = 0 [ p α , p β ] = 0 [ L α , p β 2 ] = 0 [L_{\alpha},p_{\beta}^2] = 0 [ L α , p β 2 ] = 0 [ L ⃗ ^ , p ⃗ ^ 2 ] = 0 [\hat{\vec{L}},\hat{\vec{p}}^2] = 0 [ L ^ , p ^ 2 ] = 0 L ⃗ ^ \hat{\vec{L}} L ^ ( θ , φ ) (\theta,\varphi) ( θ , φ ) [ L ⃗ ^ , V ( r ) ] = 0 [\hat{\vec{L}},V(r)] = 0 [ L ^ , V ( r )] = 0 [ L ⃗ ^ , H ^ ] = 0 [\hat{\vec{L}},\hat{H}] = 0 [ L ^ , H ^ ] = 0
自由粒子: V ( r ) = 0 V(r) = 0 V ( r ) = 0
谐振子势: V ( r ) ∝ r 2 V(r) \propto r^2 V ( r ) ∝ r 2
线性中心势: V ( r ) ∝ r V(r) \propto r V ( r ) ∝ r
对数中心势: V ( r ) ∝ ln r V(r) \propto \ln r V ( r ) ∝ ln r
球方势: V ( r ) = { 0 , r < a V 0 , r ≥ a ( V 0 可取 + ∞ , 即无限深球方势阱 ) V(r) = \begin{cases} 0 &, r<a \ V_0 &, r \ge a \end{cases} \kern 1em (V_0可取+\infty,即无限深球方势阱) V ( r ) = { 0 V 0 , r < a , r ≥ a ( V 0 可取 + ∞ , 即无限深球方势阱 )
库仑势: V ( r ) ∝ 1 r V(r) \propto \frac{1}{r} V ( r ) ∝ r 1
汤川势: V ( r ) ∝ 1 r e − α r V(r) \propto \frac{1}{r} \mathrm{e}^{-\alpha r} V ( r ) ∝ r 1 e − α r
Woods-Saxon势: V ( r ) ∝ V 0 / ( 1 + e r − R a ) V(r) \propto V_0 / (1 + \mathrm{e}^{r-\frac{R}{a}}) V ( r ) ∝ V 0 / ( 1 + e r − a R )
中心力场中力学量完全集一般选为 { H , L 2 , L z } {H,L^2,L_z} { H , L 2 , L z } ψ n l m \psi_{nlm} ψ n l m
H ^ ψ n l m = E n l ψ n l m L ^ 2 ψ n l m = l ( l + 1 ) ℏ 2 ψ n l m L ^ z ψ n l m = m ℏ ψ n l m \hat{H}\ \psi_{nlm} = E_{nl}\ \psi_{nlm} \ \hat{L}^2\ \psi_{nlm} = l(l+1)\hbar^2\ \psi_{nlm} \ \hat{L}z\ \psi {nlm} = m\hbar\ \psi_{nlm} H ^ ψ n l m = E n l ψ n l m L ^ 2 ψ n l m = l ( l + 1 ) ℏ 2 ψ n l m L ^ z ψ n l m = m ℏ ψ n l m
设质量为 μ \mu μ V ( r ) V(r) V ( r )
H ^ = p ⃗ ^ 2 2 μ + V ( r ) = − ℏ 2 2 μ ∇ 2 + V ( r ) \hat{H} = \frac{\hat{\vec{p}}^2}{2\mu} + V(r) = -\frac{\hbar^2}{2\mu} \nabla^2 + V(r) H ^ = 2 μ p ^ 2 + V ( r ) = − 2 μ ℏ 2 ∇ 2 + V ( r )
其中
∇ 2 = ∇ r 2 + 1 r 2 ∇ θ φ 2 \nabla^2 = \nabla_r^2 + \frac{1}{r^2} \nabla_{\theta\varphi}^2 ∇ 2 = ∇ r 2 + r 2 1 ∇ θφ 2
∇ r 2 = 1 r 2 ∂ ∂ r r 2 ∂ ∂ r = ∂ 2 ∂ r 2 + 2 r ∂ ∂ r = 1 r ∂ 2 ∂ r 2 r = − p ^ r 2 ℏ 2 \nabla_r^2 = \frac{1}{r^2} \frac{\partial}{\partial r} r^2 \frac{\partial}{\partial r} = \frac{\partial^2}{\partial r^2} + \frac{2}{r} \frac{\partial}{\partial r} = \frac{1}{r} \frac{\partial^2}{\partial r^2} r = -\frac{\hat{p}_r^2}{\hbar^2} ∇ r 2 = r 2 1 ∂ r ∂ r 2 ∂ r ∂ = ∂ r 2 ∂ 2 + r 2 ∂ r ∂ = r 1 ∂ r 2 ∂ 2 r = − ℏ 2 p ^ r 2
∇ θ φ 2 = 1 sin θ ∂ ∂ θ ( sin θ ∂ ∂ θ ) + 1 sin 2 θ ∂ 2 ∂ φ 2 = − L ^ 2 ℏ 2 \nabla_{\theta\varphi}^2 = \frac{1}{\sin\theta} \frac{\partial}{\partial\theta} \left( \sin\theta \frac{\partial}{\partial\theta} \right) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\varphi^2} = -\frac{\hat{L}^2}{\hbar^2} ∇ θφ 2 = sin θ 1 ∂ θ ∂ ( sin θ ∂ θ ∂ ) + sin 2 θ 1 ∂ φ 2 ∂ 2 = − ℏ 2 L ^ 2
故Hamilton算符可表示为
H ^ = p ^ r 2 2 μ + L ^ 2 2 μ r 2 + V ( r ) \hat{H} = \frac{\hat{p}_r^2}{2\mu} + \frac{\hat{L}^2}{2\mu r^2} + V(r) H ^ = 2 μ p ^ r 2 + 2 μ r 2 L ^ 2 + V ( r )
其中等号右侧第一项为径向动能 ,第二项为离心势能 ,后两项之和为有效势
V e f f = L ^ 2 2 μ r 2 + V ( r ) V_{eff} = \frac{\hat{L}^2}{2\mu r^2} + V(r) V e ff = 2 μ r 2 L ^ 2 + V ( r )
能量本征方程可表示为
[ − ℏ 2 2 μ 1 r ∂ 2 ∂ r 2 r + L ^ 2 2 μ r 2 + V ( r ) ] ψ ( r , θ , φ ) = E ψ ( r , θ , φ ) \left[ -\frac{\hbar^2}{2\mu} \frac{1}{r} \frac{\partial^2}{\partial r^2} r + \frac{\hat{L}^2}{2\mu r^2} + V(r) \right]\ \psi(r,\theta,\varphi) = E\ \psi(r,\theta,\varphi) [ − 2 μ ℏ 2 r 1 ∂ r 2 ∂ 2 r + 2 μ r 2 L ^ 2 + V ( r ) ] ψ ( r , θ , φ ) = E ψ ( r , θ , φ )
选取守恒量完全集为 { H ^ , L ^ 2 , L ^ z } {\hat{H},\hat{L}^2,\hat{L}_z} { H ^ , L ^ 2 , L ^ z } { L ^ 2 , L ^ z } {\hat{L}^2,\hat{L}_z} { L ^ 2 , L ^ z } V ( r ) V(r) V ( r )
ψ ( r , θ , φ ) = R l ( r ) Y l m ( θ , ϕ ) \psi(r,\theta,\varphi) = R_l(r) \mathrm{Y}_{lm}(\theta,\phi) ψ ( r , θ , φ ) = R l ( r ) Y l m ( θ , ϕ )
其中 l = 0 , 1 , 2 , ⋯ ; m = − l , − l + 1 , ⋯ , l − 1 , l l=0,1,2,\cdots;m=-l,-l+1,\cdots,l-1,l l = 0 , 1 , 2 , ⋯ ; m = − l , − l + 1 , ⋯ , l − 1 , l
[ − ℏ 2 2 μ 1 r ∂ 2 ∂ r 2 r + L ^ 2 2 μ r 2 + V ( r ) ] R l ( r ) Y l m ( θ , ϕ ) = E R l ( r ) Y l m ( θ , ϕ ) ⇓ [ − ℏ 2 2 μ 1 r d 2 d r 2 r + l ( l + 1 ) ℏ 2 2 μ r 2 + V ( r ) ] R l ( r ) = E R l ( r ) ⇓ 1 r d 2 d r 2 ( r R l ( r ) ) + [ 2 μ ℏ 2 ( E − V ( r ) ) − l ( l + 1 ) r 2 ] R l ( r ) = 0 \left[ -\frac{\hbar^2}{2\mu} \frac{1}{r} \frac{\partial^2}{\partial r^2} r + \frac{\hat{L}^2}{2\mu r^2} + V(r) \right]\ R_l(r) \mathrm{Y}{lm}(\theta,\phi) = E\ R_l(r) \mathrm{Y} {lm}(\theta,\phi) \ \Downarrow \ \left[ -\frac{\hbar^2}{2\mu} \frac{1}{r} \frac{\mathrm{d}^2}{\mathrm{d}r^2} r + \frac{l(l+1)\hbar^2}{2\mu r^2} + V(r) \right]\ R_l(r) = E\ R_l(r) \ \Downarrow \ \frac{1}{r} \frac{\mathrm{d}^2}{\mathrm{d}r^2} \left( r R_l(r) \right) + \left[\frac{2\mu}{\hbar^2}\left( E - V(r) \right) -\frac{l(l+1)}{r^2} \right]\ R_l(r) = 0 [ − 2 μ ℏ 2 r 1 ∂ r 2 ∂ 2 r + 2 μ r 2 L ^ 2 + V ( r ) ] R l ( r ) Y l m ( θ , ϕ ) = E R l ( r ) Y l m ( θ , ϕ ) ⇓ [ − 2 μ ℏ 2 r 1 d r 2 d 2 r + 2 μ r 2 l ( l + 1 ) ℏ 2 + V ( r ) ] R l ( r ) = E R l ( r ) ⇓ r 1 d r 2 d 2 ( r R l ( r ) ) + [ ℏ 2 2 μ ( E − V ( r ) ) − r 2 l ( l + 1 ) ] R l ( r ) = 0
令
χ l ( r ) = r R l ( r ) \chi_l(r) = r R_l(r) χ l ( r ) = r R l ( r )
则上述方程可进一步简化为
χ l ′ ′ ( r ) + [ 2 μ ℏ 2 ( E − V ( r ) ) − l ( l + 1 ) r 2 ] χ l ( r ) = 0 \chi_l''(r) + \left[\frac{2\mu}{\hbar^2}\left( E - V(r) \right) -\frac{l(l+1)}{r^2} \right]\ \chi_l(r) = 0 χ l ′′ ( r ) + [ ℏ 2 2 μ ( E − V ( r ) ) − r 2 l ( l + 1 ) ] χ l ( r ) = 0
此即中心力场中粒子需要满足的径向方程 。
波函数 χ l ( r ) \chi_l(r) χ l ( r ) l l l l l l 离心势能 产生的影响。按原子光谱的习惯,把 l = 0 , 1 , 2 , 3 , 4 , 5 , 6 , ⋯ l=0,1,2,3,4,5,6,\cdots l = 0 , 1 , 2 , 3 , 4 , 5 , 6 , ⋯ s , p , d , f , g , h , i , ⋯ s,p,d,f,g,h,i,\cdots s , p , d , f , g , h , i , ⋯
波函数 χ l ( r ) \chi_l(r) χ l ( r ) m m m l l l 2 l + 1 2l+1 2 l + 1 m m m 简并度 一般为 2 l + 1 2l+1 2 l + 1
与一维势 V ( x ) V(x) V ( x ) V ( r ) V(r) V ( r ) 定义域 为 r ≥ 0 r \ge 0 r ≥ 0 − ∞ < x < + ∞ -\infty < x < +\infty − ∞ < x < + ∞
假定势函数 V ( r ) V(r) V ( r )
lim r → 0 r 2 V ( r ) = 0 \lim_{r\to0} r^2 V(r) = 0 r → 0 lim r 2 V ( r ) = 0
(通常遇到的中心力场均满足此条件)则波函数应满足
lim r → 0 R l ( r ) ∝ r l , lim r → 0 χ l ( r ) ∝ r l + 1 \lim_{r\to0} R_l(r) \propto r^l, \kern 1em \lim_{r\to0} \chi_l(r) \propto r^{l+1} r → 0 lim R l ( r ) ∝ r l , r → 0 lim χ l ( r ) ∝ r l + 1
故
χ l ( 0 ) = 0 \chi_l(0) = 0 χ l ( 0 ) = 0
首先考虑波函数的统计诠释,粒子出现在半径为 r → 0 r\to0 r → 0
∫ 0 r R l 2 ( r ) r 2 d r ∼ r 3 R l 2 ( r ) → 0 \int_0^r R_l^2(r) r^2 \mathrm{d}r \sim r^3 R_l^2(r) \to 0 ∫ 0 r R l 2 ( r ) r 2 d r ∼ r 3 R l 2 ( r ) → 0
故若 R l ( r ) ∝ r s R_l(r) \propto r^s R l ( r ) ∝ r s s > − 3 2 s>-\frac32 s > − 2 3
当 r → 0 r\to0 r → 0 ( E − V 0 ) (E-V_0) ( E − V 0 )
d 2 d r 2 R l ( r ) + 2 r d d r R l ( r ) − l ( l + 1 ) r 2 R l ( r ) = 0 \frac{\mathrm{d}^2}{\mathrm{d}r^2} R_l(r) + \frac{2}{r} \frac{\mathrm{d}}{\mathrm{d}r} R_l(r) -\frac{l(l+1)}{r^2} R_l(r) = 0 d r 2 d 2 R l ( r ) + r 2 d r d R l ( r ) − r 2 l ( l + 1 ) R l ( r ) = 0
此方程为欧拉方程,将 R l ( r ) ∝ r s R_l(r) \propto r^s R l ( r ) ∝ r s
R l ( r ) ∝ r l 或 R l ( r ) ∝ r − ( l + 1 ) R_l(r) \propto r^l \kern 1em 或 \kern 1em R_l(r) \propto r^{-(l+1)} R l ( r ) ∝ r l 或 R l ( r ) ∝ r − ( l + 1 )
当 l ≥ 1 l\ge1 l ≥ 1 − ( l + 1 ) ≤ − 2 < − 3 2 -(l+1) \le -2 < -\frac32 − ( l + 1 ) ≤ − 2 < − 2 3 l = 0 l=0 l = 0 ∇ 2 1 r = − 4 π δ ( r ⃗ ) \nabla^2 \frac{1}{r} = -4\pi\delta(\vec{r}) ∇ 2 r 1 = − 4 π δ ( r ) R l ( r ) ∝ 1 r R_l(r) \propto \frac{1}{r} R l ( r ) ∝ r 1 r = 0 r=0 r = 0
lim r → 0 R l ( r ) ∝ r l \lim_{r\to0} R_l(r) \propto r^l r → 0 lim R l ( r ) ∝ r l
的解才可以接受。
考虑两个质量分别为 m 1 , m 2 m_1,m_2 m 1 , m 2 V ( ∣ r ⃗ 1 − r ⃗ 2 ∣ ) = V ( r ) V(|\vec{r}_1-\vec{r}_2|) = V(r) V ( ∣ r 1 − r 2 ∣ ) = V ( r )
i ℏ ∂ ∂ t ψ ( r ⃗ 1 , r ⃗ 2 , t ) = [ − ℏ 2 2 m 1 ∇ 1 2 − ℏ 2 2 m 2 ∇ 2 2 + V ( ∣ r ⃗ 1 − r ⃗ 2 ∣ ) ] ψ ( r ⃗ 1 , r ⃗ 2 , t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(\vec{r}_1,\vec{r}_2,t) = \left[ -\frac{\hbar^2}{2m_1} \nabla_1^2 - \frac{\hbar^2}{2m_2} \nabla_2^2 + V(|\vec{r}_1-\vec{r}_2|) \right] \psi(\vec{r}_1,\vec{r}_2,t) i ℏ ∂ t ∂ ψ ( r 1 , r 2 , t ) = [ − 2 m 1 ℏ 2 ∇ 1 2 − 2 m 2 ℏ 2 ∇ 2 2 + V ( ∣ r 1 − r 2 ∣ ) ] ψ ( r 1 , r 2 , t )
引入质心坐标
R ⃗ = m 1 r ⃗ 1 + m 2 r ⃗ 2 m 1 + m 2 = [ X , Y , Z ] T \vec{R} = \frac{m_1\vec{r}_1 + m_2\vec{r}_2}{m_1 + m_2} = [X,Y,Z]^T R = m 1 + m 2 m 1 r 1 + m 2 r 2 = [ X , Y , Z ] T
相对坐标
r ⃗ = r ⃗ 1 − r ⃗ 2 = [ x , y , z ] T \vec{r} = \vec{r}_1 - \vec{r}_2 = [x,y,z]^T r = r 1 − r 2 = [ x , y , z ] T
质心质量
M = m 1 + m 2 M = m_1 + m_2 M = m 1 + m 2
约化质量
μ = m 1 m 2 m 1 + m 2 \mu = \frac{m_1m_2}{m_1+m_2} μ = m 1 + m 2 m 1 m 2
此时有
∇ R 2 = ∂ 2 ∂ X 2 + ∂ 2 ∂ Y 2 + ∂ 2 ∂ Z 2 , ∇ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 1 m 1 ∇ 1 2 + 1 m 2 ∇ 2 2 = 1 M ∇ R 2 + 1 μ ∇ 2 \nabla_R^2 = \frac{\partial^2}{\partial X^2} + \frac{\partial^2}{\partial Y^2} + \frac{\partial^2}{\partial Z^2} ,\kern 1em \nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \ \ \ \frac{1}{m_1} \nabla_1^2 + \frac{1}{m_2} \nabla_2^2 = \frac{1}{M} \nabla_R^2 + \frac{1}{\mu} \nabla^2 ∇ R 2 = ∂ X 2 ∂ 2 + ∂ Y 2 ∂ 2 + ∂ Z 2 ∂ 2 , ∇ 2 = ∂ x 2 ∂ 2 + ∂ y 2 ∂ 2 + ∂ z 2 ∂ 2 m 1 1 ∇ 1 2 + m 2 1 ∇ 2 2 = M 1 ∇ R 2 + μ 1 ∇ 2
故Schrödinger方程可化为
i ℏ ∂ ∂ t ψ ( R ⃗ , r ⃗ , t ) = [ − ℏ 2 2 M ∇ R 2 − ℏ 2 2 μ ∇ 2 + V ( r ) ] ψ ( R ⃗ , r ⃗ , t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(\vec{R},\vec{r},t) = \left[ -\frac{\hbar^2}{2M} \nabla_R^2 - \frac{\hbar^2}{2\mu} \nabla^2 + V(r) \right] \psi(\vec{R},\vec{r},t) i ℏ ∂ t ∂ ψ ( R , r , t ) = [ − 2 M ℏ 2 ∇ R 2 − 2 μ ℏ 2 ∇ 2 + V ( r ) ] ψ ( R , r , t )
该方程可分离变量,设
ψ ( R ⃗ , r ⃗ , t ) = ϕ ( R ⃗ ) φ ( r ⃗ ) T ( t ) \psi(\vec{R},\vec{r},t) = \phi(\vec{R})\ \varphi(\vec{r})\ T(t) ψ ( R , r , t ) = ϕ ( R ) φ ( r ) T ( t )
则原方程可分解为三个方程
i ℏ ∂ ∂ t T ( t ) = E T T ( t ) − ℏ 2 2 M ∇ R 2 ϕ ( R ⃗ ) = E C ϕ ( R ⃗ ) [ − ℏ 2 2 μ ∇ 2 + V ( r ) ] φ ( r ⃗ ) = E φ ( r ⃗ ) \mathrm{i}\hbar \frac{\partial}{\partial t} T(t) = E_T\ T(t) \ \ \ -\frac{\hbar^2}{2M} \nabla_R^2\ \phi(\vec{R}) = E_C\ \phi(\vec{R}) \ \ \ \left[ -\frac{\hbar^2}{2\mu} \nabla^2\ + V(r) \right] \varphi(\vec{r}) = E\ \varphi(\vec{r}) i ℏ ∂ t ∂ T ( t ) = E T T ( t ) − 2 M ℏ 2 ∇ R 2 ϕ ( R ) = E C ϕ ( R ) [ − 2 μ ℏ 2 ∇ 2 + V ( r ) ] φ ( r ) = E φ ( r )
其中 E T E_T E T E C E_C E C E E E E T = E C + E E_T = E_C + E E T = E C + E
第一个方程可求出含时间部分的解为 T ( t ) = C e − i ℏ E T t T(t) = C \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_T\ t} T ( t ) = C e − ℏ i E T t
第二个方程为质心运动状态的波函数所满足的方程,质心以质量 M M M E C E_C E C
第三个方程为相对运动方程 ,其求解可参照上述对中心力场问题的分析。
采用自然单位,就是以体系的几个基本的特征量作为相应的物理量的单位。在具体的计算中,可令相应的物理量或参数为 1 1 1
自然单位的优点是,一方面运算过程的书写可以简化,另一方面是使人对体系的各种特征量的数量级有清楚的印象。此外,使用自然单位还便于研究不同体系的数学处理之间可能存在的密切关系,例如,研究各向同性谐振子势和Coulomb势中粒子的能量本征值和本征函数的关系。
常见的自然单位如下表所示:
δ \delta δ V ( x ) = γ δ ( x ) V(x)=\gamma\delta(x) V ( x ) = γ δ ( x ) 谐振子势V ( x ) = 1 2 μ ω 2 x 2 V(x)=\frac12\mu\omega^2x^2 V ( x ) = 2 1 μ ω 2 x 2 V ( ρ ) = 1 2 μ ω 2 ρ 2 V(\rho)=\frac12\mu\omega^2\rho^2 V ( ρ ) = 2 1 μ ω 2 ρ 2 V ( r ) = 1 2 μ ω 2 r 2 V(r)=\frac12\mu\omega^2r^2 V ( r ) = 2 1 μ ω 2 r 2 类氢原子(Coulomb势)κ = Z e 2 \kappa=Ze^2 κ = Z e 2 V ( r ) = − κ r V(r)=-\frac{\kappa}{r} V ( r ) = − r κ 氢原子(Coulomb势)κ = e 2 \kappa=e^2 κ = e 2 V ( r ) = − e 2 r V(r)=-\frac{e^2}{r} V ( r ) = − r e 2
自然单位 μ = ℏ = γ = 1 \mu=\hbar=\gamma=1 μ = ℏ = γ = 1 μ = ℏ = ω = 1 \mu=\hbar=\omega=1 μ = ℏ = ω = 1 μ = ℏ = κ = 1 \mu=\hbar=\kappa=1 μ = ℏ = κ = 1 μ = ℏ = e = 1 \mu=\hbar=e=1 μ = ℏ = e = 1 能量 [ E ] [E] [ E ] [ L ] [L] [ L ] [ T ] [T] [ T ] [ v ] [v] [ v ] [ p ] [p] [ p ] μ γ 2 / ℏ 2 \mu\gamma^2/\hbar^2 μ γ 2 / ℏ 2 ℏ 2 / μ γ \hbar^2/\mu\gamma ℏ 2 / μ γ ℏ 3 / μ γ 2 \hbar^3/\mu\gamma^2 ℏ 3 / μ γ 2 γ / ℏ \gamma/\hbar γ /ℏ μ γ / ℏ \mu\gamma/\hbar μ γ /ℏ ℏ ω \hbar\omega ℏ ω ℏ / μ ω \sqrt{\hbar/\mu\omega} ℏ/ μ ω ω − 1 \omega^{-1} ω − 1 ℏ ω / μ \sqrt{\hbar\omega/\mu} ℏ ω / μ μ ℏ ω \sqrt{\mu\hbar\omega} μ ℏ ω μ κ 2 / ℏ 2 \mu\kappa^2/\hbar^2 μ κ 2 / ℏ 2 ℏ 2 / μ κ \hbar^2/\mu\kappa ℏ 2 / μ κ ℏ 3 / μ κ 2 \hbar^3/\mu\kappa^2 ℏ 3 / μ κ 2 κ / ℏ \kappa/\hbar κ /ℏ μ κ / ℏ \mu\kappa/\hbar μ κ /ℏ μ e 4 / ℏ 2 \mu e^4/\hbar^2 μ e 4 / ℏ 2 ℏ 2 / μ e 2 \hbar^2/\mu e^2 ℏ 2 / μ e 2 ℏ 3 / μ e 3 \hbar^3/\mu e^3 ℏ 3 / μ e 3 e 2 / ℏ e^2/\hbar e 2 /ℏ μ e 2 / ℏ \mu e^2/\hbar μ e 2 /ℏ
考虑质量为 μ \mu μ a a a
V ( r ) = { 0 , r < a ∞ , r > a V(r)=\begin{cases} 0, & r<a \ \infty, & r>a \end{cases} V ( r ) = { 0 , ∞ , r < a r > a
该势阱中只存在束缚态 ,粒子的能量本征值 为
E n r l = ℏ 2 2 μ a 2 ξ n r l 2 ( n r = 0 , 1 , 2 , ⋯ ) E_{n_rl} = \frac{\hbar^2}{2\mu a^2} \xi_{n_rl}^2 \kern 2em (n_r=0,1,2,\cdots) E n r l = 2 μ a 2 ℏ 2 ξ n r l 2 ( n r = 0 , 1 , 2 , ⋯ )
相应的径向本征函数 为
R n r l ( r ) = { C n r l j l ( k n r l r ) , 0 ≤ r < a 0 , r > a ( k n r l = ξ n r l / a ) R_{n_rl}(r) = \begin{cases} C_{n_rl}\ \mathrm{j}l(k {n_rl}\ r) ,& 0\le r<a \ 0, & r>a \end{cases} \kern 2em (k_{n_rl} = \xi_{n_rl} / a) R n r l ( r ) = { C n r l j l ( k n r l r ) , 0 , 0 ≤ r < a r > a ( k n r l = ξ n r l / a )
其中 j l \mathrm{j}l j l 球Bessel函数 ,令 j l ( ξ ) = 0 \mathrm{j}l(\xi) = 0 j l ( ξ ) = 0 ξ n r l ( n r = 0 , 1 , 2 , ⋯ ) \xi{n_rl} \kern 1em (n_r=0,1,2,\cdots) ξ n r l ( n r = 0 , 1 , 2 , ⋯ ) ξ n r l \xi{n_rl} ξ n r l
n r = 0 n_r=0 n r = 0 n r = 1 n_r=1 n r = 1 n r = 2 n_r=2 n r = 2 n r = 3 n_r=3 n r = 3
l = 0 l=0 l = 0 π \pi π 2 π 2\pi 2 π 3 π 3\pi 3 π 4 π 4\pi 4 π l = 1 l=1 l = 1 4.493 4.493 4.493 7.725 7.725 7.725 10.904 10.904 10.904 14.066 14.066 14.066 l = 2 l=2 l = 2 5.764 5.764 5.764 9.095 9.095 9.095 12.323 12.323 12.323 15.515 15.515 15.515 l = 3 l=3 l = 3 6.988 6.988 6.988 10.417 10.417 10.417 13.698 13.698 13.698 16.924 16.924 16.924
径向本征函数中归一化系数
C n r l = [ − 2 a 3 j l − 1 ( k n r l a ) j l + 1 ( k n r l a ) ] 1 2 C_{n_rl} = \left[ -\frac{2}{a^3 \mathrm{j}{l-1}(k {n_rl}\ a) \mathrm{j}{l+1}(k {n_rl}\ a)} \right]^{\frac{1}{2}} C n r l = [ − a 3 j l − 1 ( k n r l a ) j l + 1 ( k n r l a ) 2 ] 2 1
归一化公式为
∫ 0 a R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′ \int_0^a R_{n_rl}(r)\ R_{n_r'l}(r)\ r^2 \mathrm{d}r = \delta_{n_rn_r'} ∫ 0 a R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′
对于 l = 0 l=0 l = 0 s s s
E n r 0 = π 2 ℏ 2 ( n r + 1 ) 2 2 μ a 2 ( n r = 0 , 1 , 2 , ⋯ ) E_{n_r0} = \frac{\pi^2\hbar^2(n_r+1)^2}{2\mu a^2} \kern 2em (n_r=0,1,2,\cdots) E n r 0 = 2 μ a 2 π 2 ℏ 2 ( n r + 1 ) 2 ( n r = 0 , 1 , 2 , ⋯ )
χ n r 0 ( r ) = { 2 a sin ( n r + 1 ) π r a , 0 ≤ r < a 0 , r > a \chi_{n_r0}(r) = \begin{cases} \sqrt{\frac{2}{a}} \sin \frac{(n_r+1)\pi r}{a}, & 0\le r <a \ 0, & r>a \end{cases} χ n r 0 ( r ) = { a 2 sin a ( n r + 1 ) π r , 0 , 0 ≤ r < a r > a
∫ 0 a χ n r 0 ( r ) χ n r ′ 0 ( r ) d r = δ n r n r ′ \int_0^a \chi_{n_r0}(r)\ \chi_{n_r'0}(r)\ \mathrm{d}r = \delta_{n_rn_r'} ∫ 0 a χ n r 0 ( r ) χ n r ′ 0 ( r ) d r = δ n r n r ′
在势阱外( r > a r>a r > a
R ( r ) = 0 R(r) = 0 R ( r ) = 0
在势阱内( r < a r<a r < a s s s l = 0 l=0 l = 0
χ 0 ′ ′ ( r ) + 2 μ E ℏ 2 χ 0 ( r ) = 0 \chi_0''(r) + \frac{2\mu E}{\hbar^2} \chi_0(r) = 0 χ 0 ′′ ( r ) + ℏ 2 2 μ E χ 0 ( r ) = 0
记 k = 2 μ E ℏ 2 ( E > 0 ) k = \sqrt{\frac{2\mu E}{\hbar^2}} \kern 1em (E>0) k = ℏ 2 2 μ E ( E > 0 )
χ 0 ′ ′ ( r ) + k 2 χ 0 ( r ) = 0 \chi_0''(r) + k^2 \chi_0(r) = 0 χ 0 ′′ ( r ) + k 2 χ 0 ( r ) = 0
解得
χ 0 ( r ) = A sin ( k r ) + B cos ( k r ) \chi_{0}(r) = A \sin(kr) + B \cos(kr) χ 0 ( r ) = A sin ( k r ) + B cos ( k r )
边条件为
χ 0 ( 0 ) = χ 0 ( a ) = 0 \chi_0(0) = \chi_0(a) = 0 χ 0 ( 0 ) = χ 0 ( a ) = 0
则可得
B = 0 k a = ( n r + 1 ) π ( n r = 0 , 1 , 2 , ⋯ ) B = 0 \ ka = (n_r+1)\pi \kern 2em (n_r=0,1,2,\cdots) B = 0 ka = ( n r + 1 ) π ( n r = 0 , 1 , 2 , ⋯ )
故粒子的能量本征值
E n r 0 = π 2 ℏ 2 ( n r + 1 ) 2 2 μ a 2 ( n r = 0 , 1 , 2 , ⋯ ) E_{n_r0} = \frac{\pi^2\hbar^2(n_r+1)^2}{2\mu a^2} \kern 2em (n_r=0,1,2,\cdots) E n r 0 = 2 μ a 2 π 2 ℏ 2 ( n r + 1 ) 2 ( n r = 0 , 1 , 2 , ⋯ )
归一化的波函数为
χ n r 0 ( r ) = 2 a sin ( n r + 1 ) π r a ( 0 ≤ r < a ) \chi_{n_r0}(r) = \sqrt{\frac{2}{a}} \sin \frac{(n_r+1)\pi r}{a} \kern 2em (0\le r <a) χ n r 0 ( r ) = a 2 sin a ( n r + 1 ) π r ( 0 ≤ r < a )
其次考虑 l ≠ 0 l\ne0 l = 0
R l ′ ′ ( r ) + 2 r R l ′ ( r ) + [ k 2 − l ( l + 1 ) r 2 ] R l ( r ) = 0 R_l''(r) + \frac{2}{r} R_l'(r) + \left[k^2 -\frac{l(l+1)}{r^2} \right]\ R_l(r) = 0 R l ′′ ( r ) + r 2 R l ′ ( r ) + [ k 2 − r 2 l ( l + 1 ) ] R l ( r ) = 0
边条件为
R l ( a ) = 0 R_l(a) = 0 R l ( a ) = 0
引入无量纲变量 ρ = k r \rho = kr ρ = k r
d 2 d ρ 2 R l + 2 r d d ρ R l + [ 1 − l ( l + 1 ) ρ 2 ] R l = 0 \frac{\mathrm{d}^2}{\mathrm{d}\rho^2} R_l + \frac{2}{r} \frac{\mathrm{d}}{\mathrm{d}\rho} R_l + \left[1 -\frac{l(l+1)}{\rho^2} \right]\ R_l = 0 d ρ 2 d 2 R l + r 2 d ρ d R l + [ 1 − ρ 2 l ( l + 1 ) ] R l = 0
此即球Bessel方程 ,其解可取为球Bessel函数 j l ( ρ ) \mathrm{j}_l(\rho) j l ( ρ ) n l ( ρ ) \mathrm{n}_l(\rho) n l ( ρ ) r → 0 r\to0 r → 0
j l ( ρ ) → ρ l ( 2 l + 1 ) ! ! n l ( ρ ) → − ( 2 l − 1 ) ! ! ρ l + 1 \mathrm{j}_l(\rho) \to \frac{\rho^l}{(2l+1)!!} \ \ \ \mathrm{n}_l(\rho) \to -\frac{(2l-1)!!}{\rho^{l+1}} j l ( ρ ) → ( 2 l + 1 )!! ρ l n l ( ρ ) → − ρ l + 1 ( 2 l − 1 )!!
关于Bessel方程的相关知识,请参考课本附录A6,亦可参考陈酌老师的课件 ,在此不再赘述。
考虑到 ρ = 0 \rho = 0 ρ = 0 n l ( ρ ) \mathrm{n}_l(\rho) n l ( ρ )
R l ( r ) ∝ j l ( k r ) R_l(r) \propto \mathrm{j}_l(kr) R l ( r ) ∝ j l ( k r )
根据边条件 R l ( a ) = 0 R_l(a) = 0 R l ( a ) = 0
j l ( k a ) = 0 \mathrm{j}_l(ka) = 0 j l ( ka ) = 0
故当 a a a k k k j l ( ξ ) = 0 j_{l}(\xi) = 0 j l ( ξ ) = 0 ξ n r l ( n r = 0 , 1 , 2 , ⋯ ) \xi_{n_r l} \kern 1em (n_r=0,1,2,\cdots) ξ n r l ( n r = 0 , 1 , 2 , ⋯ )
E n r l = ℏ 2 2 μ a 2 ξ n r l 2 ( n r = 0 , 1 , 2 , ⋯ ) E_{n_rl} = \frac{\hbar^2}{2\mu a^2} \xi_{n_rl}^2 \kern 2em (n_r=0,1,2,\cdots) E n r l = 2 μ a 2 ℏ 2 ξ n r l 2 ( n r = 0 , 1 , 2 , ⋯ )
相应的径向本征函数为
R n r l ( r ) = C n r l j l ( k n r l r ) ( 0 ≤ r < a ) ( k n r l = ξ n r l / a ) R_{n_rl}(r) = C_{n_rl}\ \mathrm{j}l(k {n_rl}\ r) \kern 2em (0\le r<a) \kern 2em (k_{n_rl} = \xi_{n_rl} / a) R n r l ( r ) = C n r l j l ( k n r l r ) ( 0 ≤ r < a ) ( k n r l = ξ n r l / a )
归一化系数
C n r l = [ − 2 a 3 j l − 1 ( k n r l a ) j l + 1 ( k n r l a ) ] 1 2 C_{n_rl} = \left[ -\frac{2}{a^3 \mathrm{j}{l-1}(k {n_rl}\ a) \mathrm{j}{l+1}(k {n_rl}\ a)} \right]^{\frac{1}{2}} C n r l = [ − a 3 j l − 1 ( k n r l a ) j l + 1 ( k n r l a ) 2 ] 2 1
归一化公式为
∫ 0 a R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′ \int_0^a R_{n_rl}(r)\ R_{n_r'l}(r)\ r^2 \mathrm{d}r = \delta_{n_rn_r'} ∫ 0 a R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′
当 a → ∞ a\to\infty a → ∞
lim ρ → ∞ j l ( ρ ) = 1 ρ sin ( ρ − l π 2 ) → 0 \lim_{\rho\to\infty} \mathrm{j}_l(\rho) = \frac{1}{\rho} \sin(\rho - \frac{l\pi}{2}) \to 0 ρ → ∞ lim j l ( ρ ) = ρ 1 sin ( ρ − 2 l π ) → 0
故边条件自动满足,所以 k k k E E E
R k l ( r ) = 2 π k j l ( k r ) R_{kl}(r) = \sqrt{\frac{2}{\pi}} k\ \mathrm{j}_l(kr) R k l ( r ) = π 2 k j l ( k r )
∫ 0 + ∞ R k l ( r ) R k ′ l ( r ) r 2 d r = δ ( k − k ′ ) \int_0^{+\infty} R_{kl}(r)\ R_{k'l}(r)\ r^2 \mathrm{d}r = \delta(k-k') ∫ 0 + ∞ R k l ( r ) R k ′ l ( r ) r 2 d r = δ ( k − k ′ )
考虑质量为 μ \mu μ V ( r ) V(r) V ( r )
V ( r ) = 1 2 μ ω 2 r 2 V(r) = \frac12 \mu \omega^2 r^2 V ( r ) = 2 1 μ ω 2 r 2
该势中只存在束缚态 ,粒子的能量本征值 为
E N = ( N + 3 2 ) ℏ ω ( N = 0 , 1 , 2 , ⋯ ) = ( 2 n r + l + 3 2 ) ℏ ω ( n r , l = 0 , 1 , 2 , ⋯ ) E_N = (N+\frac32) \hbar\omega \kern 2em (N=0,1,2,\cdots) \ \ \ = (2n_r + l + \frac32) \hbar\omega \kern 2em (n_r,l = 0,1,2,\cdots) E N = ( N + 2 3 ) ℏ ω ( N = 0 , 1 , 2 , ⋯ ) = ( 2 n r + l + 2 3 ) ℏ ω ( n r , l = 0 , 1 , 2 , ⋯ )
记 α = μ ω ℏ \alpha = \sqrt{\frac{\mu\omega}{\hbar}} α = ℏ μ ω 径向本征波函数 为
R n r l ( r ) = α 3 2 [ 2 l + 2 − n r ( 2 l + 2 n r + 1 ) ! ! π n r ! [ ( 2 l + 1 ) ! ! ] 2 ] 1 2 ( α r ) l e − α 2 r 2 2 F ( − n r , l + 3 2 , α 2 r 2 ) R_{n_rl}(r) = \alpha^{\frac32} \left[ \frac{2^{l+2-n_r}(2l+2n_r+1)!!}{\sqrt{\pi}n_r![(2l+1)!!]^2} \right]^{\frac12} (\alpha r)^l\ \mathrm{e}^{-\frac{\alpha^2r^2}{2}}\ \mathrm{F}(-n_r,l+\frac32,\alpha^2r^2) R n r l ( r ) = α 2 3 [ π n r ! [( 2 l + 1 )!! ] 2 2 l + 2 − n r ( 2 l + 2 n r + 1 )!! ] 2 1 ( α r ) l e − 2 α 2 r 2 F ( − n r , l + 2 3 , α 2 r 2 )
其中 F ( α , γ , ξ ) \mathrm{F}(\alpha,\gamma,\xi) F ( α , γ , ξ ) 合流超几何函数 。归一化公式为
∫ 0 + ∞ R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′ \int_0^{+\infty} R_{n_rl}(r)\ R_{n_r'l}(r)\ r^2 \mathrm{d}r = \delta_{n_rn_r'} ∫ 0 + ∞ R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′
径向方程为
R l ′ ′ ( r ) + 2 r R l ′ ( r ) + [ 2 μ ℏ 2 ( E − 1 2 μ ω 2 r 2 ) − l ( l + 1 ) r 2 ] R l ( r ) = 0 R_l''(r) + \frac{2}{r} R_l'(r) + \left[\frac{2\mu}{\hbar^2} \left(E-\frac12\mu\omega^2r^2\right) - \frac{l(l+1)}{r^2} \right]\ R_l(r) = 0 R l ′′ ( r ) + r 2 R l ′ ( r ) + [ ℏ 2 2 μ ( E − 2 1 μ ω 2 r 2 ) − r 2 l ( l + 1 ) ] R l ( r ) = 0
采用自然单位,令 ℏ = μ = ω = 1 \hbar=\mu=\omega=1 ℏ = μ = ω = 1
R l ′ ′ ( r ) + 2 r R l ′ ( r ) + [ 2 E − r 2 − l ( l + 1 ) r 2 ] R l ( r ) = 0 R_l''(r) + \frac{2}{r} R_l'(r) + \left[2E - r^2 - \frac{l(l+1)}{r^2} \right]\ R_l(r) = 0 R l ′′ ( r ) + r 2 R l ′ ( r ) + [ 2 E − r 2 − r 2 l ( l + 1 ) ] R l ( r ) = 0
考虑对方程做渐进分析以求出解的因子:
当 r → 0 r\to0 r → 0
R l ( r ) ∼ r l R_l(r) \sim r^l R l ( r ) ∼ r l
当 r → ∞ r\to\infty r → ∞
R l ′ ′ ( r ) − r 2 R l ( r ) = 0 R_l''(r) - r^2 R_l(r) = 0 R l ′′ ( r ) − r 2 R l ( r ) = 0
当 R l ( r ) ∼ e ± r 2 / 2 R_l(r) \sim \mathrm{e}^{\pm r^2/2} R l ( r ) ∼ e ± r 2 /2 R l ′ ( r ) ∼ ± r e ± r 2 / 2 R_l'(r) \sim \pm r \mathrm{e}^{\pm r^2/2} R l ′ ( r ) ∼ ± r e ± r 2 /2 R l ′ ′ ( r ) ∼ r 2 e ± r 2 / 2 ± e ± r 2 / 2 ∼ r 2 e ± r 2 / 2 R_l''(r) \sim r^2 \mathrm{e}^{\pm r^2/2} \pm \mathrm{e}^{\pm r^2/2} \sim r^2 \mathrm{e}^{\pm r^2/2} R l ′′ ( r ) ∼ r 2 e ± r 2 /2 ± e ± r 2 /2 ∼ r 2 e ± r 2 /2 R l ′ ′ ( r ) − r 2 R l ( r ) ∼ 0 R_l''(r) - r^2 R_l(r) \sim 0 R l ′′ ( r ) − r 2 R l ( r ) ∼ 0 此时有
R l ( r ) ∼ e ± r 2 / 2 R_l(r) \sim \mathrm{e}^{\pm r^2/2} R l ( r ) ∼ e ± r 2 /2
而 e r 2 / 2 \mathrm{e}^{r^2/2} e r 2 /2
R l ( r ) ∼ e − r 2 / 2 R_l(r) \sim \mathrm{e}^{-r^2/2} R l ( r ) ∼ e − r 2 /2
综上,可设
R l ( r ) = r l e − r 2 2 u ( r ) R_l(r) = r^l \mathrm{e}^{-\frac{r^2}{2}} u(r) R l ( r ) = r l e − 2 r 2 u ( r )
代入方程,可得
u ′ ′ + 2 r ( l + 1 − r 2 ) u ′ + [ 2 E − ( 2 l + 3 ) ] u = 0 u'' + \frac{2}{r}(l+1-r^2)u' + [2E-(2l+3)]u = 0 u ′′ + r 2 ( l + 1 − r 2 ) u ′ + [ 2 E − ( 2 l + 3 )] u = 0
令 ξ = r 2 \xi=r^2 ξ = r 2
ξ d 2 u d ξ 2 + ( γ − ξ ) d u d ξ − α u = 0 \xi \frac{\mathrm{d}^2u}{\mathrm{d}\xi^2} + (\gamma-\xi) \frac{\mathrm{d}u}{\mathrm{d}\xi} - \alpha u = 0 ξ d ξ 2 d 2 u + ( γ − ξ ) d ξ d u − αu = 0
该方程为合流超几何方程 ,其中参数
α = 1 2 ( l + 3 2 − E ) γ = l + 3 2 ( ≠ 整数 ) \alpha = \frac12(l+\frac32-E) \ \ \ \gamma = l + \frac32 \kern 0.5em (\ne\text{整数}) α = 2 1 ( l + 2 3 − E ) γ = l + 2 3 ( = 整数 )
合流超几何方程的求解过程如下:
先考虑方程的解在 ξ → 0 \xi\to0 ξ → 0
d 2 u d ξ 2 + γ ξ d u d ξ − α ξ u = 0 \frac{\mathrm{d}^2u}{\mathrm{d}\xi^2} + \frac{\gamma}{\xi} \frac{\mathrm{d}u}{\mathrm{d}\xi} - \frac{\alpha}{\xi} u = 0 d ξ 2 d 2 u + ξ γ d ξ d u − ξ α u = 0
将 u = ξ s u=\xi^s u = ξ s
s ( s − 1 ) ξ s − 2 + γ s ξ s − 2 − α ξ s − 1 = 0 s(s-1) \xi^{s-2} + \gamma s \xi^{s-2} - \alpha \xi^{s-1} = 0 s ( s − 1 ) ξ s − 2 + γ s ξ s − 2 − α ξ s − 1 = 0
由于 ξ → 0 \xi\to0 ξ → 0 α ξ s − 1 \alpha \xi^{s-1} α ξ s − 1
s ( s − 1 ) + γ s = 0 s(s-1) + \gamma s = 0 s ( s − 1 ) + γ s = 0
解得 s 1 = 0 , s 2 = 1 − γ s_1 = 0, s_2 = 1-\gamma s 1 = 0 , s 2 = 1 − γ s 1 = 0 s_1=0 s 1 = 0 ξ 0 \xi^0 ξ 0
u = ∑ k = 0 + ∞ c k ξ k u = \sum_{k=0}^{+\infty} c_k \xi^k u = k = 0 ∑ + ∞ c k ξ k
代入原方程可得
∑ k = 0 + ∞ [ k ( k − 1 ) c k ξ k − 1 + ( γ − ξ ) k c k ξ k − 1 − α c k ξ k ] = 0 ⇓ ∑ k = 0 + ∞ [ k ( k − 1 + γ ) c k ξ k − 1 − ( α + k ) c k ξ k ] = 0 ⇓ k ( k − 1 + γ ) c k = ( α + k − 1 ) c k − 1 ⇓ c k = α + k − 1 ( γ + k − 1 ) k c k − 1 \sum_{k=0}^{+\infty} \left[ k(k-1) c_k \xi^{k-1} + (\gamma-\xi) k c_k \xi^{k-1} - \alpha c_k \xi^k \right] = 0 \ \Downarrow \ \sum_{k=0}^{+\infty} \left[ k(k-1+\gamma) c_k \xi^{k-1} - (\alpha+k) c_k \xi^k \right] = 0 \ \Downarrow \ k(k-1+\gamma) c_k = (\alpha+k-1) c_{k-1} \ \Downarrow \ c_k = \frac{\alpha+k-1}{(\gamma+k-1)k} c_{k-1} k = 0 ∑ + ∞ [ k ( k − 1 ) c k ξ k − 1 + ( γ − ξ ) k c k ξ k − 1 − α c k ξ k ] = 0 ⇓ k = 0 ∑ + ∞ [ k ( k − 1 + γ ) c k ξ k − 1 − ( α + k ) c k ξ k ] = 0 ⇓ k ( k − 1 + γ ) c k = ( α + k − 1 ) c k − 1 ⇓ c k = ( γ + k − 1 ) k α + k − 1 c k − 1
通过 c 0 c_0 c 0
c k = α ( α + 1 ) ⋯ ( α + k − 1 ) γ ( γ + 1 ) ⋯ ( γ + k − 1 ) 1 k ! c 0 c_k = \frac{\alpha(\alpha+1)\cdots(\alpha+k-1)}{\gamma(\gamma+1)\cdots(\gamma+k-1)} \frac{1}{k!} c_0 c k = γ ( γ + 1 ) ⋯ ( γ + k − 1 ) α ( α + 1 ) ⋯ ( α + k − 1 ) k ! 1 c 0
由于 c 0 c_0 c 0 c 0 = 1 c_0=1 c 0 = 1 F ( α , γ , ξ ) \mathrm{F}(\alpha,\gamma,\xi) F ( α , γ , ξ )
u 1 = F ( α , γ , ξ ) = 1 + α γ ξ + α ( α + 1 ) γ ( γ + 1 ) ξ 2 2 ! + ⋯ = ∑ k = 0 + ∞ ( α ) k ( γ ) k ξ k k ! u_1 = \mathrm{F}(\alpha,\gamma,\xi) = 1 + \frac{\alpha}{\gamma}\xi + \frac{\alpha(\alpha+1)}{\gamma(\gamma+1)}\frac{\xi^2}{2!} + \cdots \ \ \ = \sum_{k=0}^{+\infty} \frac{(\alpha)_k}{(\gamma)_k} \frac{\xi^k}{k!} u 1 = F ( α , γ , ξ ) = 1 + γ α ξ + γ ( γ + 1 ) α ( α + 1 ) 2 ! ξ 2 + ⋯ = k = 0 ∑ + ∞ ( γ ) k ( α ) k k ! ξ k
其中
( α ) k = α ( α + 1 ) ⋯ ( α + k − 1 ) ( γ ) k = γ ( γ + 1 ) ⋯ ( γ + k − 1 ) (\alpha)_k = \alpha(\alpha+1)\cdots(\alpha+k-1) \ (\gamma)_k = \gamma(\gamma+1)\cdots(\gamma+k-1) ( α ) k = α ( α + 1 ) ⋯ ( α + k − 1 ) ( γ ) k = γ ( γ + 1 ) ⋯ ( γ + k − 1 )
显然,此级数解只当参数 γ \gamma γ
当两根之差 s 2 − s 1 = 1 − γ s_2 - s_1 = 1-\gamma s 2 − s 1 = 1 − γ
u 2 = ξ 1 − γ y u_2 = \xi^{1-\gamma} y u 2 = ξ 1 − γ y
代入原方程,可得
ξ d 2 y d ξ 2 + ( 2 − γ − ξ ) d y d ξ − ( α − γ + 1 ) y = 0 \xi \frac{\mathrm{d}^2y}{\mathrm{d}\xi^2} + (2-\gamma-\xi) \frac{\mathrm{d}y}{\mathrm{d}\xi} - (\alpha-\gamma+1) y = 0 ξ d ξ 2 d 2 y + ( 2 − γ − ξ ) d ξ d y − ( α − γ + 1 ) y = 0
其仍为合流超几何方程,只是参数不同,其解可表示为 y = F ( α − γ + 1 , 2 − γ , ξ ) y=\mathrm{F}(\alpha-\gamma+1,2-\gamma,\xi) y = F ( α − γ + 1 , 2 − γ , ξ )
u 2 = ξ 1 − γ F ( α − γ + 1 , 2 − γ , ξ ) u_2 = \xi^{1-\gamma}\ \mathrm{F}(\alpha-\gamma+1,2-\gamma,\xi) u 2 = ξ 1 − γ F ( α − γ + 1 , 2 − γ , ξ )
显然,此级数解只当 2 − γ 2-\gamma 2 − γ
回到原问题,由于 ξ 1 − γ = r − 2 l − 1 \xi^{1-\gamma} = r^{-2l-1} ξ 1 − γ = r − 2 l − 1 u 2 u_2 u 2 u 1 u_1 u 1
当 k → ∞ k\to\infty k → ∞ c k / c k − 1 ∼ 1 / k c_k/c_{k-1} \sim 1/k c k / c k − 1 ∼ 1/ k e ξ e^\xi e ξ
lim ξ → ∞ F ( α , γ , ξ ) ∼ e ξ \lim_{\xi\to\infty} \mathrm{F}(\alpha,\gamma,\xi) \sim e^{\xi} ξ → ∞ lim F ( α , γ , ξ ) ∼ e ξ
这不满足束缚态边条件,故该级数必须中断为一个多项式,通过系数的递推关系式,可得要求 ∃ k ∈ N + \exist k \in \mathbb{N}_+ ∃ k ∈ N + α + k − 1 = 0 \alpha+k-1=0 α + k − 1 = 0 α \alpha α
α = 1 2 ( l + 3 2 − E ) = − n r ( n r = 0 , 1 , 2 , ⋯ ) \alpha = \frac12(l+\frac32-E) = -n_r \kern 2em (n_r=0,1,2,\cdots) α = 2 1 ( l + 2 3 − E ) = − n r ( n r = 0 , 1 , 2 , ⋯ )
而这就是要求 E = ( 2 n r + l + 3 2 ) E=(2n_r+l+\frac32) E = ( 2 n r + l + 2 3 )
E = ( 2 n r + l + 3 2 ) ℏ ω ( n r , l = 0 , 1 , 2 , ⋯ ) E=(2n_r+l+\frac32)\hbar\omega \kern 2em (n_r,l = 0,1,2,\cdots) E = ( 2 n r + l + 2 3 ) ℏ ω ( n r , l = 0 , 1 , 2 , ⋯ )
令 N = 2 n r + l N=2n_r+l N = 2 n r + l
E = E N = ( N + 3 2 ) ℏ ω ( N = 0 , 1 , 2 , ⋯ ) E = E_N = (N+\frac32)\hbar\omega \kern 2em (N=0,1,2,\cdots) E = E N = ( N + 2 3 ) ℏ ω ( N = 0 , 1 , 2 , ⋯ )
与之相应的径向波函数(添上长度单位 α = μ ω ℏ \alpha=\sqrt{\frac{\mu\omega}{\hbar}} α = ℏ μ ω 注意此 α \alpha α )为
R n r l ( r ) ∝ r l e − α 2 r 2 2 F ( − n r , l + 3 2 , α 2 r 2 ) R_{n_rl}(r) \propto r^l\ \mathrm{e}^{-\frac{\alpha^2r^2}{2}}\ \mathrm{F}(-n_r,l+\frac32,\alpha^2r^2) R n r l ( r ) ∝ r l e − 2 α 2 r 2 F ( − n r , l + 2 3 , α 2 r 2 )
经归一化后为
R n r l ( r ) = α 3 2 [ 2 l + 2 − n r ( 2 l + 2 n r + 1 ) ! ! π n r ! [ ( 2 l + 1 ) ! ! ] 2 ] 1 2 ( α r ) l e − α 2 r 2 2 F ( − n r , l + 3 2 , α 2 r 2 ) R_{n_rl}(r) = \alpha^{\frac32} \left[ \frac{2^{l+2-n_r}(2l+2n_r+1)!!}{\sqrt{\pi}n_r![(2l+1)!!]^2} \right]^{\frac12} (\alpha r)^l\ \mathrm{e}^{-\frac{\alpha^2r^2}{2}}\ \mathrm{F}(-n_r,l+\frac32,\alpha^2r^2) R n r l ( r ) = α 2 3 [ π n r ! [( 2 l + 1 )!! ] 2 2 l + 2 − n r ( 2 l + 2 n r + 1 )!! ] 2 1 ( α r ) l e − 2 α 2 r 2 F ( − n r , l + 2 3 , α 2 r 2 )
归一化公式为
∫ 0 + ∞ R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′ \int_0^{+\infty} R_{n_rl}(r)\ R_{n_r'l}(r)\ r^2 \mathrm{d}r = \delta_{n_rn_r'} ∫ 0 + ∞ R n r l ( r ) R n r ′ l ( r ) r 2 d r = δ n r n r ′
对于给定的 N N N l l l 2 l + 1 2l+1 2 l + 1
当 N N N l = N − 2 n r l=N-2n_r l = N − 2 n r
l = N , N − 2 , N − 4 , ⋯ , 2 , 0 l = N,N-2,N-4,\cdots,2,0 l = N , N − 2 , N − 4 , ⋯ , 2 , 0
故能级简并度
f N = ∑ l ( 2 l + 1 ) = ∑ i = 0 N / 2 ( 2 × 2 i + 1 ) = 1 2 ( N + 1 ) ( N + 2 ) f_N = \sum_{l} (2l+1) = \sum_{i=0}^{N/2} (2\times2i+1) = \frac12(N+1)(N+2) f N = l ∑ ( 2 l + 1 ) = i = 0 ∑ N /2 ( 2 × 2 i + 1 ) = 2 1 ( N + 1 ) ( N + 2 )
同理,当 N N N l = N − 2 n r l=N-2n_r l = N − 2 n r
l = N , N − 2 , N − 4 , ⋯ , 3 , 1 l = N,N-2,N-4,\cdots,3,1 l = N , N − 2 , N − 4 , ⋯ , 3 , 1
故能级简并度
f N = ∑ l ( 2 l + 1 ) = ∑ i = 0 ( N − 1 ) / 2 [ 2 ( 2 i + 1 ) + 1 ] = 1 2 ( N + 1 ) ( N + 2 ) f_N = \sum_{l} (2l+1) = \sum_{i=0}^{(N-1)/2} [2(2i+1)+1] = \frac12(N+1)(N+2) f N = l ∑ ( 2 l + 1 ) = i = 0 ∑ ( N − 1 ) /2 [ 2 ( 2 i + 1 ) + 1 ] = 2 1 ( N + 1 ) ( N + 2 )
对于三维各项同性谐振子:
在球坐标系中求解得出的本征函数 ψ n r l m ( r , θ , φ ) \psi_{n_rlm}(r,\theta,\varphi) ψ n r l m ( r , θ , φ ) { H ^ , L ^ 2 , L ^ z } {\hat{H},\hat{L}^2,\hat{L}_z} { H ^ , L ^ 2 , L ^ z }
在直角坐标系中求解得出的本征函数 ϕ n x n y n z ( x , y , z ) \phi_{n_xn_yn_z}(x,y,z) ϕ n x n y n z ( x , y , z ) { H ^ x , H ^ y , H ^ z } {\hat{H}_x,\hat{H}_y,\hat{H}_z} { H ^ x , H ^ y , H ^ z }
它们之间通过一个幺正变换相联系
ψ n r l m = ∑ n x n y n z ϕ n x n y n z ∫ ϕ n x n y n z ∗ ψ n r l m d τ \psi_{n_rlm} = \sum_{n_xn_yn_z} \phi_{n_xn_yn_z} \int \phi^*{n_xn_yn_z} \psi {n_rlm} \mathrm{d}\tau ψ n r l m = n x n y n z ∑ ϕ n x n y n z ∫ ϕ n x n y n z ∗ ψ n r l m d τ
氢原子是由电子和原子核构成的两体体系,相互作用是Coulomb势(取无穷远为势能零点)
V ( r ) = − e 2 r V(r) = -\frac{e^2}{r} V ( r ) = − r e 2
将两体问题化为单体问题,约化质量为 μ \mu μ E < 0 E<0 E < 0 束缚态 ,也存在 E > 0 E>0 E > 0 游离态 ,仅考虑束缚态的解,氢原子的能量本征值 为
E n = − μ e 4 2 ℏ 2 1 n 2 = − e 2 2 a n 2 = − 13.6 1 n 2 eV ( n = 1 , 2 , 3 , ⋯ ) E_n = -\frac{\mu e^4}{2\hbar^2} \frac{1}{n^2} = -\frac{e^2}{2an^2} = -13.6 \frac{1}{n^2} \text{eV} \kern 2em (n=1,2,3,\cdots) E n = − 2 ℏ 2 μ e 4 n 2 1 = − 2 a n 2 e 2 = − 13.6 n 2 1 eV ( n = 1 , 2 , 3 , ⋯ )
其中Bohr半径 a = ℏ 2 μ e 2 a=\frac{\hbar^2}{\mu e^2} a = μ e 2 ℏ 2 主量子数
n = n r + l + 1 ( n r , l = 0 , 1 , 2 , ⋯ ) n = n_r + l + 1 \kern 2em (n_r,l = 0,1,2,\cdots) n = n r + l + 1 ( n r , l = 0 , 1 , 2 , ⋯ )
记 ξ = 2 r n a \xi = \frac{2r}{na} ξ = na 2 r 径向本征波函数 为
R n l ( r ) = N n l ξ l e − ξ 2 F ( − n + l + 1 , 2 l + 2 , ξ ) R_{nl}(r) = N_{nl}\ \xi^l\ \mathrm{e}^{-\frac{\xi}{2}}\ \mathrm{F}(-n+l+1,2l+2,\xi) R n l ( r ) = N n l ξ l e − 2 ξ F ( − n + l + 1 , 2 l + 2 , ξ )
其中 F ( α , γ , ξ ) \mathrm{F}(\alpha,\gamma,\xi) F ( α , γ , ξ ) 合流超几何函数 ,归一化系数
N n l = 2 a 3 / 2 n 2 ( 2 l + 1 ) ! ( n + l ) ! ( n − l − 1 ) ! N_{nl} = \frac{2}{a^{3/2}n^2(2l+1)!} \sqrt{\frac{(n+l)!}{(n-l-1)!}} N n l = a 3/2 n 2 ( 2 l + 1 )! 2 ( n − l − 1 )! ( n + l )!
归一化公式为
∫ 0 + ∞ R n l ( r ) R n ′ l ( r ) r 2 d r = δ n n ′ \int_0^{+\infty} R_{nl}(r)\ R_{n'l}(r)\ r^2 \mathrm{d}r = \delta_{nn'} ∫ 0 + ∞ R n l ( r ) R n ′ l ( r ) r 2 d r = δ n n ′
本征波函数 为
ψ n l m ( r , θ , φ ) = R n l ( r ) Y l m ( θ , φ ) \psi_{nlm}(r,\theta,\varphi) = R_{nl}(r) \mathrm{Y}_{lm}(\theta,\varphi) ψ n l m ( r , θ , φ ) = R n l ( r ) Y l m ( θ , φ )
其中
n = 1 , 2 , 3 , ⋯ l = 0 , 1 , 2 , ⋯ , n − 1 m = 0 , ± 1 , ± 2 , ⋯ , ± l n = 1,2,3,\cdots \ l = 0,1,2,\cdots,n-1 \ m = 0,\pm1,\pm2,\cdots,\pm l n = 1 , 2 , 3 , ⋯ l = 0 , 1 , 2 , ⋯ , n − 1 m = 0 , ± 1 , ± 2 , ⋯ , ± l
以下讨论仅限于束缚态,即 E < 0 E<0 E < 0
χ l ′ ′ ( r ) + [ 2 μ ℏ 2 ( E + e 2 r ) − l ( l + 1 ) r 2 ] χ l ( r ) = 0 \chi_l''(r) + \left[ \frac{2\mu}{\hbar^2} \left( E+\frac{e^2}{r} \right) - \frac{l(l+1)}{r^2} \right] \chi_l(r) = 0 χ l ′′ ( r ) + [ ℏ 2 2 μ ( E + r e 2 ) − r 2 l ( l + 1 ) ] χ l ( r ) = 0
边条件为
χ l ( 0 ) = 0 \chi_l(0) = 0 χ l ( 0 ) = 0
采用自然单位,令 ℏ = e = μ = 1 \hbar=e=\mu=1 ℏ = e = μ = 1
χ l ′ ′ ( r ) + [ 2 E + 2 r − l ( l + 1 ) r 2 ] χ l ( r ) = 0 \chi_l''(r) + \left[ 2E + \frac{2}{r} - \frac{l(l+1)}{r^2} \right] \chi_l(r) = 0 χ l ′′ ( r ) + [ 2 E + r 2 − r 2 l ( l + 1 ) ] χ l ( r ) = 0
考虑对方程做渐进分析以求出解的因子:
当 r → 0 r\to0 r → 0
χ l ( r ) ∝ r l + 1 \chi_l(r) \propto r^{l+1} χ l ( r ) ∝ r l + 1
当 r → ∞ r\to\infty r → ∞
χ l ′ ′ ( r ) + 2 E χ l ( r ) = 0 \chi_l''(r) + 2E\ \chi_l(r) = 0 χ l ′′ ( r ) + 2 E χ l ( r ) = 0
记 β = − 2 E \beta = \sqrt{-2E} β = − 2 E
χ l ( r ) = A e − β r + B e β r \chi_l(r) = A \mathrm{e}^{-\beta r} + B \mathrm{e}^{\beta r} χ l ( r ) = A e − β r + B e β r
由于 e β r \mathrm{e}^{\beta r} e β r
χ l ( r ) ∝ e − β r \chi_l(r) \propto \mathrm{e}^{-\beta r} χ l ( r ) ∝ e − β r
综上,可设
χ l ( r ) = r l + 1 e − β r u ( r ) \chi_l(r) = r^{l+1}\ \mathrm{e}^{-\beta r} u(r) χ l ( r ) = r l + 1 e − β r u ( r )
代入方程,可得
r u ′ ′ + [ 2 ( l + 1 ) − 2 β r ] u ′ − 2 [ ( l + 1 ) β − 1 ] u = 0 ru'' + [2(l+1) - 2\beta r] u' - 2[(l+1)\beta - 1]u = 0 r u ′′ + [ 2 ( l + 1 ) − 2 β r ] u ′ − 2 [( l + 1 ) β − 1 ] u = 0
令 ξ = 2 β r \xi = 2\beta r ξ = 2 β r
ξ d 2 u d ξ 2 + [ 2 ( l + 1 ) − ξ ] d u d ξ − [ ( l + 1 ) − 1 β ] u = 0 \xi \frac{\mathrm{d}^2u}{\mathrm{d}\xi^2} + [2(l+1) - \xi] \frac{\mathrm{d}u}{\mathrm{d}\xi} - \left[ (l+1) - \frac{1}{\beta} \right] u = 0 ξ d ξ 2 d 2 u + [ 2 ( l + 1 ) − ξ ] d ξ d u − [ ( l + 1 ) − β 1 ] u = 0
该方程为合流超几何方程 ,相应的参数为
α = l + 1 − 1 β γ = 2 ( l + 1 ) ≥ 2 ( = 正整数 ) \alpha = l + 1 - \frac{1}{\beta} \ \ \ \gamma = 2(l+1) \ge 2 \kern 0.5em (=\text{正整数}) α = l + 1 − β 1 γ = 2 ( l + 1 ) ≥ 2 ( = 正整数 )
该方程有两个解,
{ u 1 = F ( α , γ , ξ ) u 2 = ξ 1 − γ F ( α − γ + 1 , 2 − γ , ξ ) \begin{cases} u_1 = \mathrm{F}(\alpha,\gamma,\xi) \ u_2 = \xi^{1-\gamma}\ \mathrm{F}(\alpha-\gamma+1,2-\gamma,\xi) \end{cases} { u 1 = F ( α , γ , ξ ) u 2 = ξ 1 − γ F ( α − γ + 1 , 2 − γ , ξ )
在 ξ ∼ 0 \xi\sim0 ξ ∼ 0 u 2 u_2 u 2 u 1 u_1 u 1 u 1 u_1 u 1 lim ξ → + ∞ u 1 ∼ e ξ \lim_{\xi\to+\infty} u_1 \sim \mathrm{e}^\xi lim ξ → + ∞ u 1 ∼ e ξ u 1 u_1 u 1 α \alpha α
α = l + 1 − 1 β = − n r ( n r = 0 , 1 , 2 , ⋯ ) \alpha = l + 1 - \frac{1}{\beta} = -n_r \kern 2em (n_r=0,1,2,\cdots) α = l + 1 − β 1 = − n r ( n r = 0 , 1 , 2 , ⋯ )
令主量子数
n = n r + l + 1 ( n = 1 , 2 , 3 , ⋯ ) n = n_r + l + 1 \kern 2em (n=1,2,3,\cdots) n = n r + l + 1 ( n = 1 , 2 , 3 , ⋯ )
则 β = 1 n \beta=\frac{1}{n} β = n 1
E = − 1 2 β 2 = − 1 2 n 2 E = -\frac12 \beta^2 = -\frac{1}{2n^2} E = − 2 1 β 2 = − 2 n 2 1
添上能量的自然单位 μ e 4 / ℏ 2 \mu e^4/\hbar^2 μ e 4 / ℏ 2
E n = − μ e 4 2 ℏ 2 1 n 2 ( n = 1 , 2 , 3 , ⋯ ) E_n = - \frac{\mu e^4}{2\hbar^2} \frac{1}{n^2} \kern 2em (n=1,2,3,\cdots) E n = − 2 ℏ 2 μ e 4 n 2 1 ( n = 1 , 2 , 3 , ⋯ )
添上长度的自然单位,即Bohr半径 a = ℏ 2 / μ e 2 a=\hbar^2/\mu e^2 a = ℏ 2 / μ e 2 ξ = 2 r n a \xi=\frac{2r}{na} ξ = na 2 r
R n l ( r ) = χ n l ( r ) r ∝ ξ l e − ξ 2 F ( − n + l + 1 , 2 l + 2 , ξ ) R_{nl}(r) = \frac{\chi_{nl}(r)}{r} \propto \xi^l\ \mathrm{e}^{-\frac{\xi}{2}} \mathrm{F}(-n+l+1,2l+2,\xi) R n l ( r ) = r χ n l ( r ) ∝ ξ l e − 2 ξ F ( − n + l + 1 , 2 l + 2 , ξ )
对于给定的 n n n l l l 0 0 0 n − 1 n-1 n − 1
f n = ∑ l = 0 n − 1 ( 2 l + 1 ) = n 2 f_n = \sum_{l=0}^{n-1} (2l+1) = n^2 f n = l = 0 ∑ n − 1 ( 2 l + 1 ) = n 2
氢原子的能谱为混合谱,由 E < 0 E<0 E < 0 E > 0 E>0 E > 0
氢原子处于基态 ( n = 1 , l = m = 0 ) (n=1,l=m=0) ( n = 1 , l = m = 0 ) E 1 = − 13.6 eV E_1 = -13.6 \text{eV} E 1 = − 13.6 eV 0 − E 1 = 13.6 eV 0 - E_1 = 13.6 \text{eV} 0 − E 1 = 13.6 eV
对于分立谱,随着 n n n E ∼ 0 E\sim0 E ∼ 0 E ≥ 0 E\ge0 E ≥ 0
当氢原子能级从 n n n m m m h ν h\nu h ν
ν = μ e 4 4 π ℏ 3 ( 1 m 2 − 1 n 2 ) ν ~ = μ e 4 4 π ℏ 3 c ( 1 m 2 − 1 n 2 ) = R ( 1 m 2 − 1 n 2 ) \nu = \frac{\mu e^4}{4\pi\hbar^3} \left( \frac{1}{m^2} - \frac{1}{n^2} \right) \ \ \ \widetilde{\nu} = \frac{\mu e^4}{4\pi\hbar^3 c} \left( \frac{1}{m^2} - \frac{1}{n^2} \right) = R \left( \frac{1}{m^2} - \frac{1}{n^2} \right) ν = 4 π ℏ 3 μ e 4 ( m 2 1 − n 2 1 ) ν = 4 π ℏ 3 c μ e 4 ( m 2 1 − n 2 1 ) = R ( m 2 1 − n 2 1 )
其中Rydberg常数
R = μ e 4 4 π ℏ 3 c = 2 π 2 μ e 4 h 3 c R = \frac{\mu e^4}{4\pi\hbar^3 c} = \frac{2 \pi^2 \mu e^4}{h^3 c} R = 4 π ℏ 3 c μ e 4 = h 3 c 2 π 2 μ e 4
当氢原子处于 ψ n l m ( r , θ , φ ) \psi_{nlm}(r,\theta,\varphi) ψ n l m ( r , θ , φ ) ( r , θ , φ ) (r,\theta,\varphi) ( r , θ , φ ) d τ = r 2 sin θ d r d θ d φ \mathrm{d}\tau = r^2\sin\theta\mathrm{d}r\mathrm{d}\theta\mathrm{d}\varphi d τ = r 2 sin θ d r d θ d φ
W n l m d τ = ∣ ψ n l m ∣ 2 r 2 sin θ d r d θ d φ W_{nlm} \mathrm{d}\tau = |\psi_{nlm}|^2 r^2 \sin\theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi W n l m d τ = ∣ ψ n l m ∣ 2 r 2 sin θ d r d θ d φ
在球壳 ( r , r + d r ) (r,r+\mathrm{d}r) ( r , r + d r )
W n l d r = r 2 d r ∫ 4 π ∣ ψ n l m ( r , θ , φ ) ∣ 2 d Ω = [ R n l ( r ) ] 2 r 2 d r = [ χ n l ( r ) ] 2 d r W_{nl} \mathrm{d}r = r^2 \mathrm{d}r \int_{4\pi} \left|\psi_{nlm}(r,\theta,\varphi)\right|^2 \mathrm{d}\Omega = \left[R_{nl}(r)\right]^2 r^2 \mathrm{d}r = \left[\chi_{nl}(r)\right]^2 \mathrm{d}r W n l d r = r 2 d r ∫ 4 π ∣ ψ n l m ( r , θ , φ ) ∣ 2 d Ω = [ R n l ( r ) ] 2 r 2 d r = [ χ n l ( r ) ] 2 d r
χ n l \chi_{nl} χ n l R n l R_{nl} R n l n r = n − l − 1 n_r = n-l-1 n r = n − l − 1 ∣ χ n l ( r ) ∣ 2 |\chi_{nl}(r)|^2 ∣ χ n l ( r ) ∣ 2
r n = n 2 a ( n = 1 , 2 , 3 , ⋯ ) r_n = n^2 a \kern 2em (n=1,2,3,\cdots) r n = n 2 a ( n = 1 , 2 , 3 , ⋯ )
r n r_n r n
在 ( θ , φ ) (\theta,\varphi) ( θ , φ ) d Ω \mathrm{d}\Omega d Ω
W l m ( θ , φ ) d Ω = d Ω ∫ 0 + ∞ r 2 d r ∣ ψ n l m ( r , θ , φ ) ∣ 2 = ∣ Y l m ( θ , φ ) ∣ 2 d Ω W_{lm}(\theta,\varphi) \mathrm{d}\Omega = \mathrm{d}\Omega \int_{0}^{+\infty} r^2 \mathrm{d}r |\psi_{nlm}(r,\theta,\varphi)|^2 = |\mathrm{Y}_{lm}(\theta,\varphi)|^2 \mathrm{d}\Omega W l m ( θ , φ ) d Ω = d Ω ∫ 0 + ∞ r 2 d r ∣ ψ n l m ( r , θ , φ ) ∣ 2 = ∣ Y l m ( θ , φ ) ∣ 2 d Ω
故
W l m ( θ , φ ) = ∣ Y l m ( θ , φ ) ∣ 2 ∝ ∣ P l m ( cos θ ) e i m φ ∣ 2 = ∣ P l m ( cos θ ) ∣ 2 W_{lm}(\theta,\varphi) = |\mathrm{Y}{lm}(\theta,\varphi)|^2 \propto \left|\mathrm{P} {l}^{m}(\cos\theta)\mathrm{e}^{\mathrm{i}m\varphi}\right|^2 = \left|\mathrm{P}_{l}^{m}(\cos\theta)\right|^2 W l m ( θ , φ ) = ∣ Y l m ( θ , φ ) ∣ 2 ∝ P l m ( cos θ ) e i m φ 2 = ∣ P l m ( cos θ ) ∣ 2
即概率密度的角分布与 φ \varphi φ z z z
在本征态 ψ n l m \psi_{nlm} ψ n l m
j ⃗ e = − e j ⃗ = i e ℏ 2 μ ( ψ n l m ∗ ∇ ψ n l m − ψ n l m ∇ ψ n l m ∗ ) \vec{j}e = -e \vec{j} = \frac{\mathrm{i}e\hbar}{2\mu} \left( \psi^* {nlm} \nabla \psi_{nlm} - \psi_{nlm} \nabla \psi^*_{nlm} \right) j e = − e j = 2 μ i e ℏ ( ψ n l m ∗ ∇ ψ n l m − ψ n l m ∇ ψ n l m ∗ )
其中
∇ = e ⃗ r ∂ ∂ r + e ⃗ θ 1 r ∂ ∂ θ + e ⃗ φ 1 r sin θ ∂ ∂ φ \nabla = \vec{e}r \frac{\partial}{\partial r} + \vec{e} \theta \frac{1}{r} \frac{\partial}{\partial \theta} + \vec{e}_\varphi \frac{1}{r\sin\theta} \frac{\partial}{\partial \varphi} ∇ = e r ∂ r ∂ + e θ r 1 ∂ θ ∂ + e φ r sin θ 1 ∂ φ ∂
由于 ψ n l m ( r , θ , φ ) ∝ R n l ( r ) P l m ( cos θ ) e i m φ \psi_{nlm}(r,\theta,\varphi) \propto R_{nl}(r)\ P_l^m(\cos\theta)\ \mathrm{e}^{\mathrm{i}m\varphi} ψ n l m ( r , θ , φ ) ∝ R n l ( r ) P l m ( cos θ ) e i m φ R n l ( r ) R_{nl}(r) R n l ( r ) θ \theta θ P l m ( cos θ ) P_l^m(\cos\theta) P l m ( cos θ ) j r = j θ = 0 j_r = j_\theta = 0 j r = j θ = 0 φ \varphi φ e i m φ \mathrm{e}^{\mathrm{i}m\varphi} e i m φ
j φ = i e ℏ 2 μ 1 r sin θ ( ψ n l m ∗ ∂ ∂ φ ψ n l m − ψ n l m ∂ ∂ φ ψ n l m ∗ ) = i e ℏ 2 μ 1 r sin θ ( ψ n l m ∗ i m ψ n l m − ψ n l m ( − i m ) ψ n l m ∗ ) = i e ℏ 2 μ 1 r sin θ 2 i m ∣ ψ n l m ∣ 2 = − e ℏ m μ 1 r sin θ ∣ ψ n l m ∣ 2 j_\varphi = \frac{\mathrm{i}e\hbar}{2\mu} \frac{1}{r\sin\theta} \left( \psi^{nlm} \frac{\partial}{\partial \varphi} \psi {nlm} - \psi_{nlm} \frac{\partial}{\partial \varphi} \psi^{nlm} \right) \ \ \ = \frac{\mathrm{i}e\hbar}{2\mu} \frac{1}{r\sin\theta} \left( \psi^* {nlm}\ \mathrm{i}m\ \psi_{nlm} - \psi_{nlm} (-\mathrm{i}m) \psi^*{nlm} \right) \ \ \ = \frac{\mathrm{i}e\hbar}{2\mu} \frac{1}{r\sin\theta} 2\mathrm{i}m |\psi {nlm}|^2 \ \ \ = - \frac{e\hbar m}{\mu} \frac{1}{r\sin\theta} |\psi_{nlm}|^2 j φ = 2 μ i e ℏ r sin θ 1 ( ψ n l m ∗ ∂ φ ∂ ψ n l m − ψ n l m ∂ φ ∂ ψ n l m ∗ ) = 2 μ i e ℏ r sin θ 1 ( ψ n l m ∗ i m ψ n l m − ψ n l m ( − i m ) ψ n l m ∗ ) = 2 μ i e ℏ r sin θ 1 2 i m ∣ ψ n l m ∣ 2 = − μ e ℏ m r sin θ 1 ∣ ψ n l m ∣ 2
j φ j_\varphi j φ z z z d σ \mathrm{d}\sigma d σ d τ = 2 π r sin θ d σ \mathrm{d}\tau = 2\pi r \sin\theta \mathrm{d}\sigma d τ = 2 π r sin θ d σ
M z = 1 c ∫ S d I = 1 c ∫ π r 2 sin 2 θ ⋅ j φ d σ = − e ℏ m μ c ∫ π r 2 sin 2 θ r sin θ ∣ ψ n l m ∣ 2 d σ = − e ℏ m 2 μ c ∫ ∣ ψ n l m ∣ 2 ⋅ 2 π r sin θ d σ = − e ℏ m 2 μ c ∫ ∣ ψ n l m ∣ 2 d τ = − e ℏ m 2 μ c M_z = \frac{1}{c} \int S \mathrm{d}I \ \ \ = \frac{1}{c} \int \pi r^2 \sin^2\theta \cdot j_\varphi \mathrm{d}\sigma \ \ \ = - \frac{e\hbar m}{\mu c} \int \frac{\pi r^2 \sin^2\theta}{r\sin\theta} |\psi_{nlm}|^2 \mathrm{d}\sigma \ \ \ = - \frac{e\hbar m}{2\mu c} \int |\psi_{nlm}|^2 \cdot 2\pi r \sin\theta \mathrm{d}\sigma \ \ \ = - \frac{e\hbar m}{2\mu c} \int |\psi_{nlm}|^2 \mathrm{d}\tau \ \ \ = - \frac{e\hbar m}{2\mu c} M z = c 1 ∫ S d I = c 1 ∫ π r 2 sin 2 θ ⋅ j φ d σ = − μ c e ℏ m ∫ r sin θ π r 2 sin 2 θ ∣ ψ n l m ∣ 2 d σ = − 2 μ c e ℏ m ∫ ∣ ψ n l m ∣ 2 ⋅ 2 π r sin θ d σ = − 2 μ c e ℏ m ∫ ∣ ψ n l m ∣ 2 d τ = − 2 μ c e ℏ m
记Bohr磁子
μ B = e ℏ 2 μ c = 9.274 × 1 0 − 21 J ⋅ T − 1 \mu_B = \frac{e\hbar}{2\mu c} = 9.274\times10^{-21} \text{J} \cdot \text{T}^{-1} μ B = 2 μ c e ℏ = 9.274 × 1 0 − 21 J ⋅ T − 1
则轨道磁矩 μ z = M z = − m μ B \mu_z = M_z = -m \mu_B μ z = M z = − m μ B m m m m m m 磁量子数 的理由。
由此,可引入轨道磁矩算符
μ ⃗ ^ l = − μ B ℏ L ⃗ ^ \hat{\vec{\mu}}_l = - \frac{\mu_B}{\hbar} \hat{\vec{L}} μ ^ l = − ℏ μ B L ^
轨道磁矩与外磁场的作用能
W ^ = − μ ⃗ ^ l ⋅ B ⃗ = μ B ℏ L ⃗ ^ ⋅ B ⃗ \hat{W} = - \hat{\vec{\mu}}_l \cdot \vec{B} = \frac{\mu_B}{\hbar} \hat{\vec{L}} \cdot \vec{B} W ^ = − μ ^ l ⋅ B = ℏ μ B L ^ ⋅ B
离解到只剩一个电子的离子称为类氢离子 ,例如 He + , Li + + , Be + + + \text{He}^+,\text{Li}^{++},\text{Be}^{+++} He + , Li ++ , Be +++ + e +e + e + Z e +Ze + Z e μ \mu μ
类氢离子的能级公式为
E n = − μ e 4 Z 2 2 ℏ 2 n 2 = − 13.6 Z 2 n 2 eV ( n = 1 , 2 , 3 , ⋯ ) E_n = - \frac{\mu e^4 Z^2}{2 \hbar^2 n^2} = - 13.6 \frac{Z^2}{n^2}\ \text{eV} \kern 2em (n=1,2,3,\cdots) E n = − 2 ℏ 2 n 2 μ e 4 Z 2 = − 13.6 n 2 Z 2 eV ( n = 1 , 2 , 3 , ⋯ )
类氢离子从 E n → E m ( n > m ) E_n \to E_m\ (n>m) E n → E m ( n > m )
ν ~ m n = E n − E m h c = Z 2 R ( 1 m 2 − 1 n 2 ) \widetilde{\nu}_{mn} = \frac{E_n - E_m}{hc} = Z^2 R \left( \frac{1}{m^2} - \frac{1}{n^2} \right) ν mn = h c E n − E m = Z 2 R ( m 2 1 − n 2 1 )
电子不是一个质点,不是一个只具有坐标空间的三个自由度的粒子,而是还具有一个内禀自由度——”自旋 “,相应地有自旋角动量和自旋磁矩。
电子自旋角动量 S ⃗ \vec{S}, S
∣ S ⃗ ∣ = s ( s + 1 ) ℏ |\vec{S}| = \sqrt{s(s+1)} \hbar ∣ S ∣ = s ( s + 1 ) ℏ
其中 s s s 自旋量子数 。
电子自旋角动量在空间相对外磁场方向的取向也是空间量子化的,在 z z z
S z = ± ℏ 2 S_z = \pm \frac{\hbar}{2} S z = ± 2 ℏ
电子在外磁场中的两种自旋运动状态常用下图形象化地描述
应当注意的是,电子的自旋运动是一种内部“固有的”运动,而不是真正的在旋转,没有经典中的对应量。
要对电子的状态做出完全的描述,要同时考虑电子的空间坐标和自旋状态,对于自旋状态,更确切地说是要考虑在某给定方向(如 z z z s z s_z s z ψ ( r ⃗ , s z ) \psi(\vec{r},s_z) ψ ( r , s z ) s z s_z s z ± ℏ 2 \pm\frac{\hbar}{2} ± 2 ℏ 二分量波函数 方便地表示
ψ ( r ⃗ , s z ) = [ ψ ( r ⃗ , + ℏ / 2 ) ψ ( r ⃗ , − ℏ / 2 ) ] \psi(\vec{r},s_z) = \begin{bmatrix} \psi(\vec{r},+\hbar/2) \ \psi(\vec{r},-\hbar/2) \end{bmatrix} ψ ( r , s z ) = [ ψ ( r , + ℏ/2 ) ψ ( r , − ℏ/2 ) ]
称为旋量 (spinor)波函数 。
其中 ∣ ψ ( r ⃗ , ℏ / 2 ) ∣ 2 |\psi(\vec{r},\hbar/2)|^2 ∣ ψ ( r , ℏ/2 ) ∣ 2 s z = ℏ / 2 s_z = \hbar/2 s z = ℏ/2 r ⃗ \vec{r}, r ∣ ψ ( r ⃗ , − ℏ / 2 ) ∣ 2 |\psi(\vec{r},-\hbar/2)|^2 ∣ ψ ( r , − ℏ/2 ) ∣ 2 s z = − ℏ / 2 s_z = -\hbar/2 s z = − ℏ/2 r ⃗ \vec{r}, r
归一化条件 表示为
∑ s z = ± ℏ / 2 ∫ d 3 r ∣ ψ ( r ⃗ , s z ) ∣ 2 = ∫ d 3 r [ ψ ∗ ( r ⃗ , + ℏ / 2 ) ψ ∗ ( r ⃗ , − ℏ / 2 ) ] [ ψ ( r ⃗ , + ℏ / 2 ) ψ ( r ⃗ , − ℏ / 2 ) ] = ∫ d 3 r ( ∣ ψ ( r ⃗ , + ℏ 2 ) ∣ 2 + ∣ ψ ( r ⃗ , − ℏ 2 ) ∣ 2 ) = ∫ d 3 r ψ + ψ = 1 \sum_{s_z=\pm\hbar/2} \int \mathrm{d}^3r |\psi(\vec{r},s_z)|^2 \ \ \ = \int \mathrm{d}^3r \begin{bmatrix} \psi^(\vec{r},+\hbar/2) & \psi^ (\vec{r},-\hbar/2) \end{bmatrix} \begin{bmatrix} \psi(\vec{r},+\hbar/2) \ \psi(\vec{r},-\hbar/2) \end{bmatrix} \ \ \ = \int \mathrm{d}^3r \left( |\psi(\vec{r},+\frac{\hbar}{2})|^2 + |\psi(\vec{r},-\frac{\hbar}{2})|^2 \right) \ \ \ = \int \mathrm{d}^3r \psi^+ \psi = 1 s z = ± ℏ/2 ∑ ∫ d 3 r ∣ ψ ( r , s z ) ∣ 2 = ∫ d 3 r [ ψ ∗ ( r , + ℏ/2 ) ψ ∗ ( r , − ℏ/2 ) ] [ ψ ( r , + ℏ/2 ) ψ ( r , − ℏ/2 ) ] = ∫ d 3 r ( ∣ ψ ( r , + 2 ℏ ) ∣ 2 + ∣ ψ ( r , − 2 ℏ ) ∣ 2 ) = ∫ d 3 r ψ + ψ = 1
空间概率密度
ρ ( r ⃗ , s z ) = ψ + ψ = ∣ ψ ( r ⃗ , ℏ / 2 ) ∣ 2 + ∣ ψ ( r ⃗ , − ℏ / 2 ) ∣ 2 \rho(\vec{r},s_z) = \psi^+ \psi = |\psi(\vec{r},\hbar/2)|^2 + |\psi(\vec{r},-\hbar/2)|^2 ρ ( r , s z ) = ψ + ψ = ∣ ψ ( r , ℏ/2 ) ∣ 2 + ∣ ψ ( r , − ℏ/2 ) ∣ 2
自旋状态的概率
P ( + ℏ 2 ) = ∫ ∣ ψ ( r ⃗ , + ℏ 2 ) ∣ 2 d τ P ( − ℏ 2 ) = ∫ ∣ ψ ( r ⃗ , − ℏ 2 ) ∣ 2 d τ \Rho(+\frac{\hbar}{2}) = \int |\psi(\vec{r},+\frac{\hbar}{2})|^2\ \mathrm{d}\tau \ \ \ \Rho(-\frac{\hbar}{2}) = \int |\psi(\vec{r},-\frac{\hbar}{2})|^2\ \mathrm{d}\tau P ( + 2 ℏ ) = ∫ ∣ ψ ( r , + 2 ℏ ) ∣ 2 d τ P ( − 2 ℏ ) = ∫ ∣ ψ ( r , − 2 ℏ ) ∣ 2 d τ
一般情况下,自旋运动和轨道运动有相互作用,这时有
ψ ( r ⃗ , + ℏ / 2 ) ≠ ψ ( r ⃗ , − ℏ / 2 ) \psi(\vec{r},+\hbar/2) \ne \psi(\vec{r},-\hbar/2) ψ ( r , + ℏ/2 ) = ψ ( r , − ℏ/2 )
当自旋和轨道相互作用小到可以忽略时(即特殊的二分量波函数是自旋和轨道非耦合 的状态), ψ ( r ⃗ , + ℏ / 2 ) , ψ ( r ⃗ , − ℏ / 2 ) \psi(\vec{r},+\hbar/2),\psi(\vec{r},-\hbar/2) ψ ( r , + ℏ/2 ) , ψ ( r , − ℏ/2 ) r ⃗ \vec{r}, r
依赖关系是一样的,此时波函数可以分量变量,即
ψ ( r ⃗ , s z ) = ϕ ( r ⃗ ) χ ( s z ) \psi(\vec{r},s_z) = \phi(\vec{r}) \chi(s_z) ψ ( r , s z ) = ϕ ( r ) χ ( s z )
其中 χ ( s z ) \chi(s_z) χ ( s z ) 自旋波函数 ,其一般形式为
χ ( s z ) = [ a b ] \chi(s_z) = \begin{bmatrix} a \ b \end{bmatrix} χ ( s z ) = [ a b ]
式中 ∣ a ∣ 2 |a|^2 ∣ a ∣ 2 ∣ b ∣ 2 |b|^2 ∣ b ∣ 2 s z = ± ℏ / 2 s_z=\pm\hbar/2 s z = ± ℏ/2
∣ a ∣ 2 + ∣ b ∣ 2 = χ + χ = [ a ∗ b ∗ ] [ a b ] = 1 |a|^2 + |b|^2 = \chi^+ \chi = \begin{bmatrix} a^* & b^* \end{bmatrix} \begin{bmatrix} a \ b\end{bmatrix} = 1 ∣ a ∣ 2 + ∣ b ∣ 2 = χ + χ = [ a ∗ b ∗ ] [ a b ] = 1
S ⃗ ^ = S ^ x e ⃗ x + S ^ y e ⃗ y + S ^ z e ⃗ z S ^ 2 = S ^ x 2 + S ^ y 2 + S ^ z 2 \hat{\vec{S}} = \hat{S}_x \vec{e}_x + \hat{S}_y \vec{e}_y + \hat{S}_z \vec{e}_z \ \ \ \hat{S}^2 = \hat{S}_x^2 + \hat{S}_y^2 + \hat{S}_z^2 S ^ = S ^ x e x + S ^ y e y + S ^ z e z S ^ 2 = S ^ x 2 + S ^ y 2 + S ^ z 2
自旋算符 S ⃗ ^ \hat{\vec{S}} S ^ S ⃗ ^ × S ⃗ ^ = i ℏ S ⃗ ^ \hat{\vec{S}} \times \hat{\vec{S}} = \mathrm{i}\hbar\hat{\vec{S}} S ^ × S ^ = i ℏ S ^
S ⃗ ^ × S ⃗ ^ = i ℏ S ⃗ ^ { [ S ^ x , S ^ y ] = i ℏ S ^ z [ S ^ y , S ^ z ] = i ℏ S ^ x [ S ^ z , S ^ x ] = i ℏ S ^ y \hat{\vec{S}} \times \hat{\vec{S}} = \mathrm{i}\hbar\hat{\vec{S}} \begin{cases} [\hat{S}_x , \hat{S}_y] = \mathrm{i}\hbar\hat{S}_z \ [\hat{S}_y , \hat{S}_z] = \mathrm{i}\hbar\hat{S}_x \ [\hat{S}_z , \hat{S}_x] = \mathrm{i}\hbar\hat{S}_y \end{cases} S ^ × S ^ = i ℏ S ^ ⎩ ⎨ ⎧ [ S ^ x , S ^ y ] = i ℏ S ^ z [ S ^ y , S ^ z ] = i ℏ S ^ x [ S ^ z , S ^ x ] = i ℏ S ^ y
[ S ^ 2 , S ^ x ] = [ S ^ 2 , S ^ y ] = [ S ^ 2 , S ^ z ] = 0 [\hat{S}^2 , \hat{S}_x] = [\hat{S}^2 , \hat{S}_y] = [\hat{S}^2 , \hat{S}_z] = 0 [ S ^ 2 , S ^ x ] = [ S ^ 2 , S ^ y ] = [ S ^ 2 , S ^ z ] = 0
{ S ^ 2 , S ^ z } {\hat{S}^2 , \hat{S}_z} { S ^ 2 , S ^ z } ∣ s m ⟩ |sm\rangle ∣ s m ⟩
S ^ 2 ∣ s m ⟩ = s ( s + 1 ) ℏ 2 ∣ s m ⟩ S ^ z ∣ s m ⟩ = m ℏ ∣ s m ⟩ \hat{S}^2\ |sm\rangle = s(s+1)\hbar^2\ |sm\rangle \ \hat{S}_z\ |sm\rangle = m\hbar\ |sm\rangle S ^ 2 ∣ s m ⟩ = s ( s + 1 ) ℏ 2 ∣ s m ⟩ S ^ z ∣ s m ⟩ = m ℏ ∣ s m ⟩
其中 s = 0 , 1 2 , 1 , 3 2 , ⋯ s=0,\frac12,1,\frac32,\cdots s = 0 , 2 1 , 1 , 2 3 , ⋯ m = − s , − s + 1 , ⋯ , s − 1 , s m=-s,-s+1,\cdots,s-1,s m = − s , − s + 1 , ⋯ , s − 1 , s
对于电子, s = 1 2 s=\frac12 s = 2 1 S ⃗ \vec{S}, S ± ℏ 2 \pm\frac{\hbar}{2} ± 2 ℏ S ^ x , S ^ y , S ^ z \hat{S}_x , \hat{S}_y , \hat{S}_z S ^ x , S ^ y , S ^ z ± ℏ 2 \pm\frac{\hbar}{2} ± 2 ℏ
此时在 { S ^ 2 , S ^ z } {\hat{S}^2,\hat{S}_z} { S ^ 2 , S ^ z } ∣ 1 2 , ± 1 2 ⟩ | \frac12 , \pm\frac12 \rangle ∣ 2 1 , ± 2 1 ⟩ ∣ ± ⟩ | \pm \rangle ∣ ± ⟩
S ^ 2 ∣ ± ⟩ = 3 4 ℏ 2 ∣ ± ⟩ S ^ z ∣ ± ⟩ = ± 1 2 ℏ ∣ ± ⟩ \hat{S}^2\ |\pm\rangle = \frac34\hbar^2\ |\pm\rangle \ \ \ \hat{S}_z\ |\pm\rangle = \pm\frac12\hbar\ |\pm\rangle S ^ 2 ∣ ± ⟩ = 4 3 ℏ 2 ∣ ± ⟩ S ^ z ∣ ± ⟩ = ± 2 1 ℏ ∣ ± ⟩
为了使自旋算符单位化、无量纲化,引入Pauli算符 σ ⃗ ^ \hat{\vec{\sigma}} σ ^
S ⃗ ^ = ℏ 2 σ ⃗ ^ \hat{\vec{S}} = \frac{\hbar}{2} \hat{\vec{\sigma}} S ^ = 2 ℏ σ ^
Pauli算符的分量算符本征值均为 ± 1 \pm1 ± 1
σ ^ x 2 = σ ^ y 2 = σ ^ z 2 = I \hat{\sigma}_x^2 = \hat{\sigma}_y^2 = \hat{\sigma}_z^2 = I σ ^ x 2 = σ ^ y 2 = σ ^ z 2 = I
Pauli算符是厄米算符 ,即 σ ⃗ ^ + = σ ⃗ ^ \hat{\vec{\sigma}}^+ = \hat{\vec{\sigma}} σ ^ + = σ ^
[ σ ^ 2 , σ ^ x ] = [ σ ^ 2 , σ ^ y ] = [ σ ^ 2 , σ ^ z ] = 0 [\hat{\sigma}^2 , \hat{\sigma}_x] = [\hat{\sigma}^2 , \hat{\sigma}_y] = [\hat{\sigma}^2 , \hat{\sigma}_z] = 0 [ σ ^ 2 , σ ^ x ] = [ σ ^ 2 , σ ^ y ] = [ σ ^ 2 , σ ^ z ] = 0
σ ⃗ ^ × σ ⃗ ^ = 2 i σ ⃗ ^ { [ σ ^ x , σ ^ y ] = 2 i σ ^ z [ σ ^ y , σ ^ z ] = 2 i σ ^ x [ σ ^ z , σ ^ x ] = 2 i σ ^ y \hat{\vec{\sigma}} \times \hat{\vec{\sigma}} = 2\mathrm{i}\hat{\vec{\sigma}} \begin{cases} [\hat{\sigma}_x , \hat{\sigma}_y] = 2\mathrm{i}\hat{\sigma}_z \ [\hat{\sigma}_y , \hat{\sigma}_z] = 2\mathrm{i}\hat{\sigma}_x \ [\hat{\sigma}_z , \hat{\sigma}_x] = 2\mathrm{i}\hat{\sigma}_y \end{cases} σ ^ × σ ^ = 2 i σ ^ ⎩ ⎨ ⎧ [ σ ^ x , σ ^ y ] = 2 i σ ^ z [ σ ^ y , σ ^ z ] = 2 i σ ^ x [ σ ^ z , σ ^ x ] = 2 i σ ^ y
将 σ ^ x 2 = σ ^ y 2 = σ ^ z 2 = I \hat{\sigma}_x^2 = \hat{\sigma}_y^2 = \hat{\sigma}_z^2 = I σ ^ x 2 = σ ^ y 2 = σ ^ z 2 = I σ ⃗ ^ \hat{\vec{\sigma}} σ ^ 反对易 ,即
{ σ ^ x σ ^ y + σ ^ y σ ^ x = 0 σ ^ y σ ^ z + σ ^ z σ ^ y = 0 σ ^ z σ ^ x + σ ^ x σ ^ z = 0 \begin{cases} \hat{\sigma}_x \hat{\sigma}_y + \hat{\sigma}_y \hat{\sigma}_x = 0 \ \hat{\sigma}_y \hat{\sigma}_z + \hat{\sigma}_z \hat{\sigma}_y = 0 \ \hat{\sigma}_z \hat{\sigma}_x + \hat{\sigma}_x \hat{\sigma}_z = 0 \end{cases} ⎩ ⎨ ⎧ σ ^ x σ ^ y + σ ^ y σ ^ x = 0 σ ^ y σ ^ z + σ ^ z σ ^ y = 0 σ ^ z σ ^ x + σ ^ x σ ^ z = 0
进一步可得
{ σ x σ y = − σ y σ x = i σ z σ y σ z = − σ z σ y = i σ x σ z σ x = − σ x σ z = i σ y \begin{cases} \sigma_x \sigma_y = - \sigma_y \sigma_x = \mathrm{i} \sigma_z \ \sigma_y \sigma_z = - \sigma_z \sigma_y = \mathrm{i} \sigma_x \ \sigma_z \sigma_x = - \sigma_x \sigma_z = \mathrm{i} \sigma_y \ \end{cases} ⎩ ⎨ ⎧ σ x σ y = − σ y σ x = i σ z σ y σ z = − σ z σ y = i σ x σ z σ x = − σ x σ z = i σ y
这组式子可归纳为
σ α σ β = δ α β + i ∑ γ ε α β γ σ γ \sigma_\alpha \sigma_\beta = \delta_{\alpha\beta} + \mathrm{i} \sum_\gamma \varepsilon_{\alpha\beta\gamma} \sigma_\gamma σ α σ β = δ α β + i γ ∑ ε α β γ σ γ
该式与 σ ⃗ ^ + = σ ⃗ ^ \hat{\vec{\sigma}}^+ = \hat{\vec{\sigma}} σ ^ + = σ ^
在 { S ^ 2 , S ^ z } {\hat{S}^2,\hat{S}_z} { S ^ 2 , S ^ z } { σ ^ 2 , σ ^ z } {\hat{\sigma}^2,\hat{\sigma}_z} { σ ^ 2 , σ ^ z } Pauli矩阵 :
σ ^ x = [ 0 1 1 0 ] σ ^ y = [ 0 − i i 0 ] σ ^ z = [ 1 0 0 − 1 ] \hat{\sigma}_x = \begin{bmatrix} 0 & 1 \ 1 & 0 \end{bmatrix} \kern 2em \hat{\sigma}_y = \begin{bmatrix} 0 & -\mathrm{i} \ \mathrm{i} & 0 \end{bmatrix} \kern 2em \hat{\sigma}_z = \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix} σ ^ x = [ 0 1 1 0 ] σ ^ y = [ 0 i − i 0 ] σ ^ z = [ 1 0 0 − 1 ]
Pauli矩阵是厄米 、自逆 、零迹 的。
在 { σ ^ 2 , σ ^ z } {\hat{\sigma}^2,\hat{\sigma}_z} { σ ^ 2 , σ ^ z } σ ^ z \hat{\sigma}_z σ ^ z ± 1 \pm1 ± 1
σ ^ z = [ 1 0 0 − 1 ] \hat{\sigma}_z = \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix} σ ^ z = [ 1 0 0 − 1 ]
设
σ ^ x = [ a b c d ] \hat{\sigma}_x = \begin{bmatrix} a & b \ c & d \end{bmatrix} σ ^ x = [ a c b d ]
根据 σ z σ x = − σ x σ z \sigma_z \sigma_x = - \sigma_x \sigma_z σ z σ x = − σ x σ z
[ a b c d ] [ 1 0 0 − 1 ] = − [ 1 0 0 − 1 ] [ a b c d ] ⇓ [ a − b c − d ] = [ − a − b c d ] ⇓ a = d = 0 \begin{bmatrix} a & b \ c & d \end{bmatrix} \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix} = - \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix} \begin{bmatrix} a & b \ c & d \end{bmatrix} \ \Downarrow \ \begin{bmatrix} a & -b \ c & -d \end{bmatrix} = \begin{bmatrix} -a & -b \ c & d \end{bmatrix} \ \Downarrow \ a = d = 0 [ a c b d ] [ 1 0 0 − 1 ] = − [ 1 0 0 − 1 ] [ a c b d ] ⇓ [ a c − b − d ] = [ − a c − b d ] ⇓ a = d = 0
再根据厄米性 σ ⃗ ^ + = σ ⃗ ^ \hat{\vec{\sigma}}^+ = \hat{\vec{\sigma}} σ ^ + = σ ^ c = b ∗ c = b^* c = b ∗
σ ^ x = [ 0 b b ∗ 0 ] \hat{\sigma}_x = \begin{bmatrix} 0 & b \ b^* & 0 \end{bmatrix} σ ^ x = [ 0 b ∗ b 0 ]
最后,根据 σ ^ x 2 = I \hat{\sigma}_x^2 = I σ ^ x 2 = I
σ ^ x 2 = [ 0 b b ∗ 0 ] [ 0 b b ∗ 0 ] = [ ∣ b ∣ 2 0 0 ∣ b ∣ 2 ] = I \hat{\sigma}_x^2 = \begin{bmatrix} 0 & b \ b^* & 0 \end{bmatrix} \begin{bmatrix} 0 & b \ b^* & 0 \end{bmatrix} = \begin{bmatrix} |b|^2 & 0 \ 0 & |b|^2 \end{bmatrix} = I σ ^ x 2 = [ 0 b ∗ b 0 ] [ 0 b ∗ b 0 ] = [ ∣ b ∣ 2 0 0 ∣ b ∣ 2 ] = I
故 ∣ b ∣ = 1 |b| = 1 ∣ b ∣ = 1 b = e i δ b = \mathrm{e}^{\mathrm{i}\delta} b = e i δ δ = 0 \delta=0 δ = 0 b = 1 b=1 b = 1
σ ^ x = [ 0 1 1 0 ] \hat{\sigma}_x = \begin{bmatrix} 0 & 1 \ 1 & 0 \end{bmatrix} σ ^ x = [ 0 1 1 0 ]
根据 σ z σ x = i σ y \sigma_z \sigma_x = \mathrm{i} \sigma_y σ z σ x = i σ y
σ ^ y = − i σ z σ x = − i [ 1 0 0 − 1 ] [ 0 1 1 0 ] = [ 0 − i i 0 ] \hat{\sigma}_y = - \mathrm{i} \sigma_z \sigma_x = - \mathrm{i} \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix} \begin{bmatrix} 0 & 1 \ 1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & -\mathrm{i} \ \mathrm{i} & 0 \end{bmatrix} σ ^ y = − i σ z σ x = − i [ 1 0 0 − 1 ] [ 0 1 1 0 ] = [ 0 i − i 0 ]
实验发现电子自旋磁矩等于一个玻尔磁子,即
∣ μ z ∣ = μ B = e ℏ 2 m e |\mu_z| = \mu_B = \frac{e\hbar}{2m_e} ∣ μ z ∣ = μ B = 2 m e e ℏ
定义电子自旋磁矩算符 为
μ ⃗ ^ s = − 2 μ B ℏ S ⃗ ^ = − e m e S ⃗ ^ \hat{\vec{\mu}}_s = -2 \frac{\mu_B}{\hbar} \hat{\vec{S}} = - \frac{e}{m_e} \hat{\vec{S}} μ ^ s = − 2 ℏ μ B S ^ = − m e e S ^
在 z z z
μ ^ s z ∣ ± ⟩ = − 2 μ B ℏ S ^ z ∣ ± ⟩ = − 2 μ B ℏ ( ± ℏ 2 ) ∣ ± ⟩ = ∓ μ B ∣ ± ⟩ \hat{\mu}_{sz} |\pm\rangle = -2 \frac{\mu_B}{\hbar} \hat{S}_z |\pm\rangle = -2 \frac{\mu_B}{\hbar} (\pm\frac{\hbar}{2}) |\pm\rangle = \mp \mu_B |\pm\rangle μ ^ sz ∣ ± ⟩ = − 2 ℏ μ B S ^ z ∣ ± ⟩ = − 2 ℏ μ B ( ± 2 ℏ ) ∣ ± ⟩ = ∓ μ B ∣ ± ⟩
轨道磁矩
μ ⃗ ^ l = g l μ B ℏ L ⃗ ^ \hat{\vec{\mu}}_l = g_l \frac{\mu_B}{\hbar} \hat{\vec{L}} μ ^ l = g l ℏ μ B L ^
自旋磁矩
μ ⃗ ^ s = g s μ B ℏ S ⃗ ^ \hat{\vec{\mu}}_s = g_s \frac{\mu_B}{\hbar} \hat{\vec{S}} μ ^ s = g s ℏ μ B S ^
其中旋磁比
g l = − 1 , g s = − 2 g_l = -1, \kern 2em g_s = -2 g l = − 1 , g s = − 2
电子磁矩与外磁场的相互作用能
W = − ( μ ⃗ ^ l + μ ⃗ ^ s ) ⋅ B ⃗ W = - (\hat{\vec{\mu}}_l + \hat{\vec{\mu}}_s) \cdot \vec{B} W = − ( μ ^ l + μ ^ s ) ⋅ B
若外磁场 B ⃗ = B 0 e ⃗ z \vec{B} = B_0 \vec{e}_z B = B 0 e z
W = − ( μ ⃗ ^ l + μ ⃗ ^ s ) ⋅ B ⃗ = μ B B 0 ℏ ( L ⃗ ^ z + 2 S ⃗ ^ z ) W = - (\hat{\vec{\mu}}_l + \hat{\vec{\mu}}_s) \cdot \vec{B} = \frac{\mu_B B_0}{\hbar} (\hat{\vec{L}}_z + 2\hat{\vec{S}}_z) W = − ( μ ^ l + μ ^ s ) ⋅ B = ℏ μ B B 0 ( L ^ z + 2 S ^ z )
若矢量算符 J ⃗ ^ \hat{\vec{J}}, J ^
J ⃗ ^ × J ⃗ ^ = i ℏ J ⃗ ^ { [ J ^ x , J ^ y ] = i ℏ J ^ z [ J ^ y , J ^ z ] = i ℏ J ^ x [ J ^ z , J ^ x ] = i ℏ J ^ y \hat{\vec{J}} \times \hat{\vec{J}} = \mathrm{i}\hbar\hat{\vec{J}} \begin{cases} [\hat{J}_x , \hat{J}_y] = \mathrm{i}\hbar\hat{J}_z \ [\hat{J}_y , \hat{J}_z] = \mathrm{i}\hbar\hat{J}_x \ [\hat{J}_z , \hat{J}_x] = \mathrm{i}\hbar\hat{J}_y \end{cases} J ^ × J ^ = i ℏ J ^ ⎩ ⎨ ⎧ [ J ^ x , J ^ y ] = i ℏ J ^ z [ J ^ y , J ^ z ] = i ℏ J ^ x [ J ^ z , J ^ x ] = i ℏ J ^ y
则称 J ⃗ ^ \hat{\vec{J}}, J ^ 角动量算符 ,定义角动量平方算符
J ^ 2 = J ^ x 2 + J ^ y 2 + J ^ z 2 \hat{J}^2 = \hat{J}_x^2 + \hat{J}_y^2 + \hat{J}_z^2 J ^ 2 = J ^ x 2 + J ^ y 2 + J ^ z 2
其满足
[ J ^ 2 , J ^ α ] = 0 ( α = x , y , z ) [\hat{J}^2 , \hat{J}_\alpha] = 0 \kern 2em (\alpha=x,y,z) [ J ^ 2 , J ^ α ] = 0 ( α = x , y , z )
定义角动量的升降算符
J ^ ± = J ^ x ± i J ^ y \hat{J}_\pm = \hat{J}_x \pm \mathrm{i}\hat{J}_y J ^ ± = J ^ x ± i J ^ y
其中 J + J_+ J + 升算符 (raising operator), J − J_- J − 降算符 (lowering operator)。
升降算符不是厄米算符,其满足
J ^ ± + = J ^ ∓ \hat{J}\pm^+ = \hat{J} \mp J ^ ± + = J ^ ∓
以下只给出结论,证明从略。
[ J ^ + , J ^ − ] = 2 ℏ J ^ z [\hat{J}+ , \hat{J} -] = 2\hbar \hat{J}_z [ J ^ + , J ^ − ] = 2ℏ J ^ z
[ J ^ x , J ^ ± ] = ∓ ℏ J ^ z [ J ^ y , J ^ ± ] = − i ℏ J ^ z [ J ^ z , J ^ ± ] = ± ℏ J ^ ± \ [\hat{J}x , \hat{J} \pm] = \mp \hbar \hat{J}_z \ \ [\hat{J}y , \hat{J} \pm] = -\mathrm{i} \hbar \hat{J}z \ \ [\hat{J}z , \hat{J} \pm] = \pm \hbar \hat{J} \pm [ J ^ x , J ^ ± ] = ∓ ℏ J ^ z [ J ^ y , J ^ ± ] = − i ℏ J ^ z [ J ^ z , J ^ ± ] = ± ℏ J ^ ±
[ J ^ 2 , J ^ ± ] = 0 [\hat{J}^2 , \hat{J}_\pm] = 0 [ J ^ 2 , J ^ ± ] = 0
J ^ x = 1 2 ( J ^ + + J ^ − ) J ^ y = 1 2 i ( J ^ + − J ^ − ) \hat{J}x = \frac12 (\hat{J} + + \hat{J}-) \kern 2em \hat{J}y = \frac{1}{2\mathrm{i}} (\hat{J} + - \hat{J} -) J ^ x = 2 1 ( J ^ + + J ^ − ) J ^ y = 2 i 1 ( J ^ + − J ^ − )
对于任意类型的角动量(如轨道角动量、自旋角动量、总角动量等),本征值谱为
J ^ 2 ∣ j m ⟩ = j ( j + 1 ) ℏ 2 ∣ j m ⟩ J ^ z ∣ j m ⟩ = m ℏ ∣ j m ⟩ \hat{J}^2\ |jm\rangle = j(j+1)\hbar^2\ |jm\rangle \ \ \ \hat{J}_z\ |jm\rangle = m\hbar\ |jm\rangle J ^ 2 ∣ jm ⟩ = j ( j + 1 ) ℏ 2 ∣ jm ⟩ J ^ z ∣ jm ⟩ = m ℏ ∣ jm ⟩
其中量子数
j = 0 , 1 2 , 1 , 3 2 , 2 , ⋯ m = − j , − j + 1 , ⋯ , j − 1 , j j = 0,\frac12,1,\frac32,2,\cdots \ \ \ m = -j,-j+1,\cdots,j-1,j j = 0 , 2 1 , 1 , 2 3 , 2 , ⋯ m = − j , − j + 1 , ⋯ , j − 1 , j
对于轨道角动量
j = l = 0 , 1 , 2 , ⋯ m = 0 , ± 1 , ± 2 , ⋯ , ± j j = l = 0,1,2,\cdots \ \ \ m = 0,\pm1,\pm2,\cdots,\pm j j = l = 0 , 1 , 2 , ⋯ m = 0 , ± 1 , ± 2 , ⋯ , ± j
对于电子自旋角动量
j = 1 2 m = ± 1 2 j = \frac12 \ \ \ m = \pm \frac12 j = 2 1 m = ± 2 1
角动量 { J ^ 2 , J ^ z } {\hat{J}^2,\hat{J}_z} { J ^ 2 , J ^ z }
J ^ 2 ∣ λ m ⟩ = λ ℏ 2 ∣ λ m ⟩ J ^ z ∣ λ m ⟩ = m ℏ ∣ λ m ⟩ \hat{J}^2\ |\lambda m\rangle = \lambda\hbar^2\ |\lambda m\rangle \ \ \ \hat{J}_z\ |\lambda m\rangle = m\hbar\ |\lambda m\rangle J ^ 2 ∣ λm ⟩ = λ ℏ 2 ∣ λm ⟩ J ^ z ∣ λm ⟩ = m ℏ ∣ λm ⟩
需要求出 λ , m \lambda,m λ , m
首先,根据 [ J ^ 2 , J ^ + ] = 0 [\hat{J}^2 , \hat{J}_+] = 0 [ J ^ 2 , J ^ + ] = 0
⟨ λ ′ m ′ ∣ [ J ^ 2 , J ^ + ] ∣ λ m ⟩ = 0 \langle \lambda'm'| [\hat{J}^2 , \hat{J}_+] | \lambda m \rangle = 0 ⟨ λ ′ m ′ ∣ [ J ^ 2 , J ^ + ] ∣ λm ⟩ = 0
结合 J ^ 2 ∣ λ m ⟩ = λ ℏ 2 ∣ λ m ⟩ \hat{J}^2\ |\lambda m\rangle = \lambda\hbar^2\ |\lambda m\rangle J ^ 2 ∣ λm ⟩ = λ ℏ 2 ∣ λm ⟩
⇓ ⟨ λ ′ m ′ ∣ J ^ 2 J ^ + − J ^ + J ^ 2 ∣ λ m ⟩ = 0 ⇓ ⟨ λ ′ m ′ ∣ J ^ 2 J ^ + ∣ λ m ⟩ − ⟨ λ ′ m ′ ∣ J ^ + J ^ 2 ∣ λ m ⟩ = 0 ⇓ λ ′ ℏ 2 ⟨ λ ′ m ′ ∣ J ^ + ∣ λ m ⟩ − λ ℏ 2 ⟨ λ ′ m ′ ∣ J ^ + ∣ λ m ⟩ = 0 ⇓ ( λ ′ − λ ) ⟨ λ ′ m ′ ∣ J ^ + ∣ λ m ⟩ = 0 \Downarrow \ \langle \lambda'm'| \hat{J}^2\hat{J}+ - \hat{J} +\hat{J}^2 | \lambda m \rangle = 0 \ \Downarrow \ \langle \lambda'm'| \hat{J}^2\hat{J}+ | \lambda m \rangle - \langle \lambda'm'| \hat{J} +\hat{J}^2 | \lambda m \rangle = 0 \ \Downarrow \ \lambda'\hbar^2 \langle \lambda'm'| \hat{J}+ | \lambda m \rangle - \lambda\hbar^2 \langle \lambda'm'| \hat{J} + | \lambda m \rangle = 0 \ \Downarrow \ (\lambda'-\lambda) \langle \lambda'm'| \hat{J}_+ | \lambda m \rangle = 0 ⇓ ⟨ λ ′ m ′ ∣ J ^ 2 J ^ + − J ^ + J ^ 2 ∣ λm ⟩ = 0 ⇓ ⟨ λ ′ m ′ ∣ J ^ 2 J ^ + ∣ λm ⟩ − ⟨ λ ′ m ′ ∣ J ^ + J ^ 2 ∣ λm ⟩ = 0 ⇓ λ ′ ℏ 2 ⟨ λ ′ m ′ ∣ J ^ + ∣ λm ⟩ − λ ℏ 2 ⟨ λ ′ m ′ ∣ J ^ + ∣ λm ⟩ = 0 ⇓ ( λ ′ − λ ) ⟨ λ ′ m ′ ∣ J ^ + ∣ λm ⟩ = 0
当 λ ′ ≠ λ \lambda' \ne \lambda λ ′ = λ ⟨ λ ′ m ′ ∣ J + ∣ λ m ⟩ = 0 \langle \lambda'm'| J_+ | \lambda m \rangle = 0 ⟨ λ ′ m ′ ∣ J + ∣ λm ⟩ = 0 λ ′ = λ \lambda' = \lambda λ ′ = λ ⟨ λ ′ m ′ ∣ J + ∣ λ m ⟩ \langle \lambda'm'| J_+ | \lambda m \rangle ⟨ λ ′ m ′ ∣ J + ∣ λm ⟩
⟨ λ ′ m ′ ∣ J ^ + ∣ λ m ⟩ = δ λ ′ λ ⟨ λ m ′ ∣ J ^ + ∣ λ m ⟩ \langle \lambda'm'| \hat{J}+ | \lambda m \rangle = \delta {\lambda'\lambda} \langle \lambda m'| \hat{J}_+ | \lambda m \rangle ⟨ λ ′ m ′ ∣ J ^ + ∣ λm ⟩ = δ λ ′ λ ⟨ λ m ′ ∣ J ^ + ∣ λm ⟩
由于推导该式子时只用了 [ J 2 , J + ] = 0 [J^2 , J_+] = 0 [ J 2 , J + ] = 0 J ^ + , J ^ x , J ^ y , J ^ z \hat{J}_+,\hat{J}_x,\hat{J}_y,\hat{J}_z J ^ + , J ^ x , J ^ y , J ^ z
接下来,根据对易关系 [ J ^ z , J ^ ± ] = ± ℏ J ^ ± [\hat{J}z , \hat{J} \pm] = \pm \hbar \hat{J}_\pm [ J ^ z , J ^ ± ] = ± ℏ J ^ ± J ^ z ∣ λ m ⟩ = m ℏ ∣ λ m ⟩ \hat{J}_z\ |\lambda m\rangle = m\hbar\ |\lambda m\rangle J ^ z ∣ λm ⟩ = m ℏ ∣ λm ⟩
⟨ λ m ′ ∣ [ J ^ z , J ^ ± ] ∣ λ m ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λ m ⟩ ⇓ ⟨ λ m ′ ∣ J ^ z J ^ ± − J ^ ± J ^ z ∣ λ m ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λ m ⟩ ⇓ ⟨ λ m ′ ∣ J ^ z J ^ ± ∣ λ m ⟩ − ⟨ λ m ′ ∣ J ^ ± J ^ z ∣ λ m ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λ m ⟩ ⇓ m ′ ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λ m ⟩ − m ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λ m ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λ m ⟩ ⇓ ( m ′ − m ∓ 1 ) ⟨ λ m ′ ∣ J ^ ± ∣ λ m ⟩ = 0 ⇓ ⟨ λ ′ m ′ ∣ J ^ ± ∣ λ m ⟩ = δ λ ′ λ δ m ′ , m ± 1 ⟨ λ , m ± 1 ∣ J ^ ± ∣ λ m ⟩ \langle \lambda m'| [\hat{J}z , \hat{J} \pm] | \lambda m \rangle = \pm \hbar \langle \lambda m'| \hat{J}\pm | \lambda m \rangle \ \Downarrow \ \langle \lambda m'| \hat{J}z\hat{J} \pm - \hat{J} \pm\hat{J}z | \lambda m \rangle = \pm \hbar \langle \lambda m'| \hat{J} \pm | \lambda m \rangle \ \Downarrow \ \langle \lambda m'| \hat{J}z\hat{J} \pm | \lambda m \rangle - \langle \lambda m'| \hat{J}\pm\hat{J}z | \lambda m \rangle = \pm \hbar \langle \lambda m'| \hat{J} \pm | \lambda m \rangle \ \Downarrow \ m'\hbar \langle \lambda m'| \hat{J} \pm | \lambda m \rangle - m\hbar \langle \lambda m'| \hat{J}\pm | \lambda m \rangle = \pm \hbar \langle \lambda m'| \hat{J} \pm | \lambda m \rangle \ \Downarrow \ (m'-m\mp1) \langle \lambda m'| \hat{J}\pm | \lambda m \rangle = 0 \ \Downarrow \ \langle \lambda'm'| \hat{J} \pm | \lambda m \rangle = \delta_{\lambda'\lambda} \delta_{m',m\pm1} \langle \lambda,m\pm1 | \hat{J}_\pm | \lambda m \rangle ⟨ λ m ′ ∣ [ J ^ z , J ^ ± ] ∣ λm ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λm ⟩ ⇓ ⟨ λ m ′ ∣ J ^ z J ^ ± − J ^ ± J ^ z ∣ λm ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λm ⟩ ⇓ ⟨ λ m ′ ∣ J ^ z J ^ ± ∣ λm ⟩ − ⟨ λ m ′ ∣ J ^ ± J ^ z ∣ λm ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λm ⟩ ⇓ m ′ ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λm ⟩ − m ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λm ⟩ = ± ℏ ⟨ λ m ′ ∣ J ^ ± ∣ λm ⟩ ⇓ ( m ′ − m ∓ 1 ) ⟨ λ m ′ ∣ J ^ ± ∣ λm ⟩ = 0 ⇓ ⟨ λ ′ m ′ ∣ J ^ ± ∣ λm ⟩ = δ λ ′ λ δ m ′ , m ± 1 ⟨ λ , m ± 1∣ J ^ ± ∣ λm ⟩
这说明算符 J ^ ± \hat{J}_\pm J ^ ± m m m 1 1 1
然后,根据对易关系 [ J ^ + , J ^ − ] = 2 ℏ J ^ z [\hat{J}+ , \hat{J} -] = 2\hbar \hat{J}_z [ J ^ + , J ^ − ] = 2ℏ J ^ z
⟨ λ m ′ ∣ [ J ^ + , J ^ − ] ∣ λ m ⟩ = 2 ℏ ⟨ λ m ′ ∣ J ^ z ∣ λ m ⟩ ⇓ ⟨ λ m ′ ∣ J ^ + J ^ − − J ^ − J ^ + ∣ λ m ⟩ = 2 m ℏ 2 δ m ′ m ⇓ ⟨ λ m ∣ J ^ + J ^ − ∣ λ m ⟩ − ⟨ λ m ∣ J ^ − J ^ + ∣ λ m ⟩ = 2 m ℏ 2 ⇓ ∑ m ′ ′ ⟨ λ m ∣ J ^ + ∣ λ m ′ ′ ⟩ ⟨ λ m ′ ′ ∣ J ^ − ∣ λ m ⟩ − ⟨ λ m ∣ J ^ − ∣ λ m ′ ′ ⟩ ⟨ λ m ′ ′ ∣ J ^ + ∣ λ m ⟩ = 2 m ℏ 2 ⇓ ⟨ λ m ∣ J ^ + ∣ λ , m − 1 ⟩ ⟨ λ , m − 1 ∣ J ^ − ∣ λ m ⟩ − ⟨ λ m ∣ J ^ − ∣ λ , m + 1 ⟩ ⟨ λ , m + 1 ∣ J ^ + ∣ λ m ⟩ = 2 m ℏ 2 ⇓ ⟨ λ m ∣ J ^ + ∣ λ , m − 1 ⟩ ⟨ λ , m − 1 ∣ J ^ + ∣ λ m ⟩ ∗ − ⟨ λ m ∣ J ^ + ∣ λ , m + 1 ⟩ ∗ ⟨ λ , m + 1 ∣ J ^ + ∣ λ m ⟩ = 2 m ℏ 2 ⇓ ∣ ⟨ λ m ∣ J ^ + ∣ λ , m − 1 ⟩ ∣ 2 − ∣ ⟨ λ , m + 1 ∣ J ^ + ∣ λ m ⟩ ∣ 2 = 2 m ℏ 2 \langle \lambda m' | [\hat{J}+ , \hat{J} -] | \lambda m \rangle = 2\hbar \langle \lambda m'| \hat{J}z | \lambda m \rangle \ \Downarrow \ \langle \lambda m' | \hat{J} +\hat{J}- - \hat{J} -\hat{J}+ | \lambda m \rangle = 2m\hbar^2 \delta {m'm} \ \Downarrow \ \langle \lambda m | \hat{J}+\hat{J} - | \lambda m \rangle - \langle \lambda m | \hat{J}-\hat{J} + | \lambda m \rangle = 2m\hbar^2 \ \Downarrow \ \sum_{m''} \langle \lambda m | \hat{J}+ | \lambda m'' \rangle \langle \lambda m ''| \hat{J} - | \lambda m \rangle - \langle \lambda m | \hat{J}- | \lambda m'' \rangle \langle \lambda m ''| \hat{J} + | \lambda m \rangle = 2m\hbar^2 \ \Downarrow \ \langle \lambda m | \hat{J}+ | \lambda,m-1 \rangle \langle \lambda,m-1 | \hat{J} - | \lambda m \rangle - \langle \lambda m | \hat{J}- | \lambda,m+1 \rangle \langle \lambda,m+1 | \hat{J} + | \lambda m \rangle = 2m\hbar^2 \ \Downarrow \ \langle \lambda m | \hat{J}+ | \lambda,m-1 \rangle \langle \lambda,m-1 | \hat{J} + | \lambda m \rangle^* - \langle \lambda m | \hat{J}+ | \lambda,m+1 \rangle^* \langle \lambda,m+1 | \hat{J} + | \lambda m \rangle = 2m\hbar^2 \ \Downarrow \ \left| \langle \lambda m | \hat{J}+ | \lambda,m-1 \rangle \right|^2 - \left| \langle \lambda,m+1 | \hat{J} + | \lambda m \rangle \right|^2 = 2m\hbar^2 ⟨ λ m ′ ∣ [ J ^ + , J ^ − ] ∣ λm ⟩ = 2ℏ ⟨ λ m ′ ∣ J ^ z ∣ λm ⟩ ⇓ ⟨ λ m ′ ∣ J ^ + J ^ − − J ^ − J ^ + ∣ λm ⟩ = 2 m ℏ 2 δ m ′ m ⇓ ⟨ λm ∣ J ^ + J ^ − ∣ λm ⟩ − ⟨ λm ∣ J ^ − J ^ + ∣ λm ⟩ = 2 m ℏ 2 ⇓ m ′′ ∑ ⟨ λm ∣ J ^ + ∣ λ m ′′ ⟩ ⟨ λ m ′′ ∣ J ^ − ∣ λm ⟩ − ⟨ λm ∣ J ^ − ∣ λ m ′′ ⟩ ⟨ λ m ′′ ∣ J ^ + ∣ λm ⟩ = 2 m ℏ 2 ⇓ ⟨ λm ∣ J ^ + ∣ λ , m − 1 ⟩ ⟨ λ , m − 1∣ J ^ − ∣ λm ⟩ − ⟨ λm ∣ J ^ − ∣ λ , m + 1 ⟩ ⟨ λ , m + 1∣ J ^ + ∣ λm ⟩ = 2 m ℏ 2 ⇓ ⟨ λm ∣ J ^ + ∣ λ , m − 1 ⟩ ⟨ λ , m − 1∣ J ^ + ∣ λm ⟩ ∗ − ⟨ λm ∣ J ^ + ∣ λ , m + 1 ⟩ ∗ ⟨ λ , m + 1∣ J ^ + ∣ λm ⟩ = 2 m ℏ 2 ⇓ ⟨ λm ∣ J ^ + ∣ λ , m − 1 ⟩ 2 − ⟨ λ , m + 1∣ J ^ + ∣ λm ⟩ 2 = 2 m ℏ 2
令 ξ m ℏ = ⟨ λ , m + 1 ∣ J ^ + ∣ λ m ⟩ = ⟨ λ m ∣ J ^ − ∣ λ , m + 1 ⟩ ∗ \xi_{m}\hbar = \langle \lambda,m+1 | \hat{J}+ | \lambda m \rangle = \langle \lambda m | \hat{J} - | \lambda,m+1 \rangle^* ξ m ℏ = ⟨ λ , m + 1∣ J ^ + ∣ λm ⟩ = ⟨ λm ∣ J ^ − ∣ λ , m + 1 ⟩ ∗
∣ ξ m − 1 ∣ 2 − ∣ ξ m ∣ 2 = 2 m |\xi_{m-1}|^2 - |\xi_m|^2 = 2m ∣ ξ m − 1 ∣ 2 − ∣ ξ m ∣ 2 = 2 m
此方程的解为
∣ ξ m ∣ 2 = C − m ( m + 1 ) |\xi_m|^2 = C - m(m+1) ∣ ξ m ∣ 2 = C − m ( m + 1 )
其中 C C C m m m ∣ ξ m ∣ 2 ≥ 0 |\xi_m|^2 \ge 0 ∣ ξ m ∣ 2 ≥ 0
m ( m + 1 ) ≤ C m(m+1) \le C m ( m + 1 ) ≤ C
这表明量子数 m m m m m m m ‾ \overline{m} m m ‾ \underline{m} m m > m ‾ m>\overline{m} m > m m < m ‾ m<\underline{m} m < m ⟨ λ m ∣ λ m ⟩ = 0 \langle \lambda m | \lambda m \rangle = 0 ⟨ λm ∣ λm ⟩ = 0
ξ m ‾ = 1 ℏ ⟨ λ , m ‾ + 1 ∣ J ^ + ∣ λ m ‾ ⟩ = 1 ℏ ⟨ λ , m ‾ + 1 ∣ λ , m ‾ + 1 ⟩ = 0 \xi_{\overline{m}} = \frac{1}{\hbar} \langle \lambda,\overline{m}+1 | \hat{J}_+ | \lambda \overline{m} \rangle = \frac{1}{\hbar} \langle \lambda,\overline{m}+1 | \lambda,\overline{m}+1 \rangle = 0 ξ m = ℏ 1 ⟨ λ , m + 1∣ J ^ + ∣ λ m ⟩ = ℏ 1 ⟨ λ , m + 1∣ λ , m + 1 ⟩ = 0
故 C = m ‾ ( m ‾ + 1 ) C = \overline{m}(\overline{m}+1) C = m ( m + 1 )
ξ m ‾ − 1 = 1 ℏ ⟨ λ , m ‾ − 1 ∣ J ^ − ∣ λ m ‾ ⟩ ∗ = 1 ℏ ⟨ λ , m ‾ − 1 ∣ λ , m ‾ − 1 ⟩ ∗ = 0 \xi_{\underline{m}-1} = \frac{1}{\hbar} \langle \lambda,\underline{m}-1 | \hat{J}_- | \lambda \underline{m} \rangle^* = \frac{1}{\hbar} \langle \lambda,\underline{m}-1 | \lambda,\underline{m}-1 \rangle^* = 0 ξ m − 1 = ℏ 1 ⟨ λ , m − 1∣ J ^ − ∣ λ m ⟩ ∗ = ℏ 1 ⟨ λ , m − 1∣ λ , m − 1 ⟩ ∗ = 0
故 C = m ‾ ( m ‾ − 1 ) C = \underline{m}(\underline{m}-1) C = m ( m − 1 ) C C C
m ‾ = − m ‾ \underline{m} = - \overline{m} m = − m
由于相邻的两个 m m m 1 1 1 m m m
m ‾ − m ‾ = 非负整数 ⇓ 2 m ‾ = 非负整数 ⇓ m ‾ = 非负整数 2 \overline{m} - \underline{m} = 非负整数 \ \Downarrow \ 2\overline{m} = 非负整数 \ \Downarrow \ \overline{m} = \frac{非负整数}{2} m − m = 非负整数 ⇓ 2 m = 非负整数 ⇓ m = 2 非负整数
记 m ‾ = j \overline{m} = j m = j j j j 1 2 \frac12 2 1
j = { 1 2 , 3 2 , 5 2 , ⋯ ( 半奇数 ) 0 , 1 , 2 , ⋯ ( 非负整数 ) j = \begin{cases} \frac12,\frac32,\frac52,\cdots & (半奇数) \ 0,1,2,\cdots & (非负整数) \end{cases} j = { 2 1 , 2 3 , 2 5 , ⋯ 0 , 1 , 2 , ⋯ ( 半奇数 ) ( 非负整数 )
故
∣ ξ m ∣ 2 = C − m ( m + 1 ) = m ‾ ( m ‾ + 1 ) − m ( m + 1 ) = j ( j + 1 ) − m ( m + 1 ) = ( j − m ) ( j + m + 1 ) |\xi_m|^2 = C - m(m+1) = \overline{m}(\overline{m}+1) - m(m+1) = j(j+1) - m(m+1) \ \ \ = (j-m)(j+m+1) ∣ ξ m ∣ 2 = C − m ( m + 1 ) = m ( m + 1 ) − m ( m + 1 ) = j ( j + 1 ) − m ( m + 1 ) = ( j − m ) ( j + m + 1 )
通过以上推导,已经得出了量子数 j j j m m m λ \lambda λ j j j J ^ 2 \hat{J}^2 J ^ 2 J ^ z \hat{J}_z J ^ z
J ^ 2 = J ^ x 2 + J ^ y 2 + J ^ z 2 = 1 4 ( J ^ + + J ^ − ) 2 − 1 4 ( J ^ + − J ^ − ) 2 + J ^ z 2 = 1 2 ( J ^ + J ^ − + J ^ − J ^ + ) + J ^ z 2 \hat{J}^2 = \hat{J}x^2 + \hat{J}y^2 + \hat{J}z^2 \ \ \ = \frac14 (\hat{J} + + \hat{J} -)^2 - \frac14 (\hat{J} + - \hat{J}-)^2 + \hat{J}z^2 \ \ \ = \frac12 (\hat{J} +\hat{J} - + \hat{J}-\hat{J} +) + \hat{J}_z^2 J ^ 2 = J ^ x 2 + J ^ y 2 + J ^ z 2 = 4 1 ( J ^ + + J ^ − ) 2 − 4 1 ( J ^ + − J ^ − ) 2 + J ^ z 2 = 2 1 ( J ^ + J ^ − + J ^ − J ^ + ) + J ^ z 2
两边取平均值可得
⟨ λ m ∣ J ^ 2 ∣ λ m ⟩ = 1 2 ⟨ λ m ∣ J ^ + J ^ − + J ^ − J ^ + ∣ λ m ⟩ + ⟨ λ m ∣ J ^ z 2 ∣ λ m ⟩ ⇓ λ ℏ 2 = 1 2 ( ⟨ λ m ∣ J ^ + J ^ − ∣ λ m ⟩ + ⟨ λ m ∣ J ^ − J ^ + ∣ λ m ⟩ ) + m 2 ℏ 2 ⇓ λ ℏ 2 = 1 2 ∑ m ′ ( ⟨ λ m ∣ J ^ + ∣ λ m ′ ⟩ ⟨ λ m ′ ∣ J ^ − ∣ λ m ⟩ + ⟨ λ m ∣ J ^ − ∣ λ m ′ ⟩ ⟨ λ m ′ ∣ J ^ + ∣ λ m ⟩ ) + m 2 ℏ 2 ⇓ λ ℏ 2 = 1 2 ( ⟨ λ m ∣ J ^ + ∣ λ , m − 1 ⟩ ⟨ λ , m − 1 ∣ J ^ − ∣ λ m ⟩ + ⟨ λ m ∣ J ^ − ∣ λ , m + 1 ⟩ ⟨ λ , m + 1 ∣ J ^ + ∣ λ m ⟩ ) + m 2 ℏ 2 ⇓ λ ℏ 2 = ℏ 2 2 ( ∣ ξ m − 1 ∣ 2 + ∣ ξ m ∣ 2 ) + m 2 ℏ 2 ⇓ λ = 1 2 [ ( j − m + 1 ) ( j + m ) + ( j − m ) ( j + m + 1 ) ] + m 2 ⇓ λ = j ( j + 1 ) \langle \lambda m | \hat{J}^2 | \lambda m \rangle = \frac12 \langle \lambda m| \hat{J}+\hat{J} - + \hat{J}-\hat{J} + | \lambda m \rangle + \langle \lambda m| \hat{J}z^2 | \lambda m \rangle \ \Downarrow \ \lambda \hbar^2 = \frac12 \left( \langle \lambda m| \hat{J} +\hat{J}- | \lambda m \rangle + \langle \lambda m| \hat{J} -\hat{J}+ | \lambda m \rangle \right) + m^2 \hbar^2 \ \Downarrow \ \lambda \hbar^2 = \frac12 \sum {m'} \left( \langle \lambda m| \hat{J}+ | \lambda m' \rangle \langle \lambda m' | \hat{J} - | \lambda m \rangle + \langle \lambda m| \hat{J}- | \lambda m' \rangle \langle \lambda m' | \hat{J} + | \lambda m \rangle \right) + m^2 \hbar^2 \ \Downarrow \ \lambda \hbar^2 = \frac12 \left( \langle \lambda m| \hat{J}+ | \lambda,m-1 \rangle \langle \lambda,m-1 | \hat{J} - | \lambda m \rangle + \langle \lambda m| \hat{J}- | \lambda,m+1 \rangle \langle \lambda,m+1 | \hat{J} + | \lambda m \rangle \right) + m^2 \hbar^2 \ \Downarrow \ \lambda \hbar^2 = \frac{\hbar^2}{2} \left( |\xi_{m-1}|^2 + |\xi_m|^2 \right) + m^2 \hbar^2 \ \Downarrow \ \lambda = \frac12 \left[ (j-m+1)(j+m) + (j-m)(j+m+1) \right] + m^2 \ \Downarrow \ \lambda = j(j+1) ⟨ λm ∣ J ^ 2 ∣ λm ⟩ = 2 1 ⟨ λm ∣ J ^ + J ^ − + J ^ − J ^ + ∣ λm ⟩ + ⟨ λm ∣ J ^ z 2 ∣ λm ⟩ ⇓ λ ℏ 2 = 2 1 ( ⟨ λm ∣ J ^ + J ^ − ∣ λm ⟩ + ⟨ λm ∣ J ^ − J ^ + ∣ λm ⟩ ) + m 2 ℏ 2 ⇓ λ ℏ 2 = 2 1 m ′ ∑ ( ⟨ λm ∣ J ^ + ∣ λ m ′ ⟩ ⟨ λ m ′ ∣ J ^ − ∣ λm ⟩ + ⟨ λm ∣ J ^ − ∣ λ m ′ ⟩ ⟨ λ m ′ ∣ J ^ + ∣ λm ⟩ ) + m 2 ℏ 2 ⇓ λ ℏ 2 = 2 1 ( ⟨ λm ∣ J ^ + ∣ λ , m − 1 ⟩ ⟨ λ , m − 1∣ J ^ − ∣ λm ⟩ + ⟨ λm ∣ J ^ − ∣ λ , m + 1 ⟩ ⟨ λ , m + 1∣ J ^ + ∣ λm ⟩ ) + m 2 ℏ 2 ⇓ λ ℏ 2 = 2 ℏ 2 ( ∣ ξ m − 1 ∣ 2 + ∣ ξ m ∣ 2 ) + m 2 ℏ 2 ⇓ λ = 2 1 [ ( j − m + 1 ) ( j + m ) + ( j − m ) ( j + m + 1 ) ] + m 2 ⇓ λ = j ( j + 1 )
综上,即完成了本征值的求解。
在 { J ^ 2 , J ^ z } {\hat{J}^2,\hat{J}_z} { J ^ 2 , J ^ z } J ^ 2 , J ^ z \hat{J}^2,\hat{J}_z J ^ 2 , J ^ z
⟨ j ′ m ′ ∣ J ^ 2 ∣ j m ⟩ = j ( j + 1 ) ℏ 2 δ j j ′ δ m m ′ ⟨ j ′ m ′ ∣ J ^ z ∣ j m ⟩ = m ℏ δ j j ′ δ m m ′ \langle j'm'| \hat{J}^2 | jm \rangle = j(j+1) \hbar^2\ \delta_{jj'} \delta_{mm'} \ \ \ \langle j'm'| \hat{J}z | jm \rangle = m \hbar\ \delta {jj'} \delta_{mm'} ⟨ j ′ m ′ ∣ J ^ 2 ∣ jm ⟩ = j ( j + 1 ) ℏ 2 δ j j ′ δ m m ′ ⟨ j ′ m ′ ∣ J ^ z ∣ jm ⟩ = m ℏ δ j j ′ δ m m ′
其余的角动量相关算符对 j j j m m m
⟨ j , m + 1 ∣ J ^ + ∣ j m ⟩ = ℏ j ( j + 1 ) − m ( m + 1 ) ⟨ j , m − 1 ∣ J ^ − ∣ j m ⟩ = ℏ j ( j + 1 ) − m ( m − 1 ) \langle j,m+1 | \hat{J}+ | jm \rangle = \hbar \sqrt{j(j+1) - m(m+1)} \ \ \ \langle j,m-1 | \hat{J} - | jm \rangle = \hbar \sqrt{j(j+1) - m(m-1)} ⟨ j , m + 1∣ J ^ + ∣ jm ⟩ = ℏ j ( j + 1 ) − m ( m + 1 ) ⟨ j , m − 1∣ J ^ − ∣ jm ⟩ = ℏ j ( j + 1 ) − m ( m − 1 )
角动量在 x , y x,y x , y
⟨ j , m + 1 ∣ J ^ x ∣ j m ⟩ = ℏ 2 j ( j + 1 ) − m ( m + 1 ) ⟨ j , m − 1 ∣ J ^ x ∣ j m ⟩ = ℏ 2 j ( j + 1 ) − m ( m − 1 ) ⟨ j , m + 1 ∣ J ^ y ∣ j m ⟩ = − i ℏ 2 j ( j + 1 ) − m ( m + 1 ) ⟨ j , m − 1 ∣ J ^ y ∣ j m ⟩ = i ℏ 2 j ( j + 1 ) − m ( m − 1 ) \langle j,m+1 | \hat{J}_x | jm \rangle = \frac{\hbar}{2} \sqrt{j(j+1) - m(m+1)} \ \ \ \langle j,m-1 | \hat{J}_x | jm \rangle = \frac{\hbar}{2} \sqrt{j(j+1) - m(m-1)} \ \ \ \langle j,m+1 | \hat{J}_y | jm \rangle = -\frac{\mathrm{i}\hbar}{2} \sqrt{j(j+1) - m(m+1)} \ \ \ \langle j,m-1 | \hat{J}_y | jm \rangle = \frac{\mathrm{i}\hbar}{2} \sqrt{j(j+1) - m(m-1)} ⟨ j , m + 1∣ J ^ x ∣ jm ⟩ = 2 ℏ j ( j + 1 ) − m ( m + 1 ) ⟨ j , m − 1∣ J ^ x ∣ jm ⟩ = 2 ℏ j ( j + 1 ) − m ( m − 1 ) ⟨ j , m + 1∣ J ^ y ∣ jm ⟩ = − 2 i ℏ j ( j + 1 ) − m ( m + 1 ) ⟨ j , m − 1∣ J ^ y ∣ jm ⟩ = 2 i ℏ j ( j + 1 ) − m ( m − 1 )
实际上,角动量的升降算符与 x , y x,y x , y e i δ \mathrm{e}^{\mathrm{i}\delta} e i δ δ = 0 \delta = 0 δ = 0
设设角动量 J ⃗ ^ 1 \hat{\vec{J}}_1 J ^ 1 J ⃗ ^ 2 \hat{\vec{J}}_2 J ^ 2
[ J ^ 1 α , J ^ 2 β ] = 0 ( α , β = x , y , z ) [\hat{J}{1\alpha} , \hat{J} {2\beta}] = 0 \kern 2em (\alpha,\beta = x,y,z) [ J ^ 1 α , J ^ 2 β ] = 0 ( α , β = x , y , z )
则矢量和 J ⃗ ^ = J ⃗ ^ 1 + J ⃗ ^ 2 \hat{\vec{J}} = \hat{\vec{J}}_1 + \hat{\vec{J}}_2 J ^ = J ^ 1 + J ^ 2 总角动量 ,它是厄米算符,且满足角动量的一般对易关系,即
J ⃗ ^ × J ⃗ ^ = i ℏ J ⃗ ^ \hat{\vec{J}} \times \hat{\vec{J}} = \mathrm{i}\hbar \hat{\vec{J}} J ^ × J ^ = i ℏ J ^
由于两个角动量 J ⃗ ^ 1 \hat{\vec{J}}_1 J ^ 1 J ⃗ ^ 2 \hat{\vec{J}}_2 J ^ 2
[ J ^ 1 2 , J ⃗ ^ 2 ] = [ J ^ 2 2 , J ⃗ ^ 1 ] = 0 [\hat{J}_1^2 , \hat{\vec{J}}_2] = [\hat{J}_2^2 , \hat{\vec{J}}_1] = 0 [ J ^ 1 2 , J ^ 2 ] = [ J ^ 2 2 , J ^ 1 ] = 0
由此容易推得
[ J ^ 1 2 , J ⃗ ^ ] = [ J ^ 2 2 , J ⃗ ^ ] = 0 [ J ^ 1 2 , J ^ 2 ] = [ J ^ 2 2 , J ^ 2 ] = 0 \ [\hat{J}_1^2 , \hat{\vec{J}}] = [\hat{J}_2^2 , \hat{\vec{J}}] = 0 \ \ \ \ [\hat{J}_1^2 , \hat{J}^2] = [\hat{J}_2^2 , \hat{J}^2] = 0 [ J ^ 1 2 , J ^ ] = [ J ^ 2 2 , J ^ ] = 0 [ J ^ 1 2 , J ^ 2 ] = [ J ^ 2 2 , J ^ 2 ] = 0
根据 J α = J 1 α + J 2 α J_\alpha = J_{1\alpha} + J_{2\alpha} J α = J 1 α + J 2 α [ J 1 α , J 2 α ] = 0 [J_{1\alpha} , J_{2\alpha}] = 0 [ J 1 α , J 2 α ] = 0
[ J ^ α , J ^ 1 α ] = [ J ^ α , J ^ 2 α ] = 0 ( α = x , y , z ) [\hat{J}\alpha , \hat{J} {1\alpha}] = [\hat{J}{\alpha} , \hat{J} {2\alpha}] = 0 \kern 2em (\alpha = x,y,z) [ J ^ α , J ^ 1 α ] = [ J ^ α , J ^ 2 α ] = 0 ( α = x , y , z )
根据 [ J ^ α , J ^ β ] = ε α β γ i ℏ J ^ γ [\hat{J}{\alpha} , \hat{J} {\beta}] = \varepsilon_{\alpha\beta\gamma} \mathrm{i}\hbar \hat{J}_{\gamma} [ J ^ α , J ^ β ] = ε α β γ i ℏ J ^ γ
J ^ 2 = ( J ^ 1 + J ^ 2 ) 2 = J ^ 1 2 + J ^ 2 2 + 2 J ^ 1 ⋅ J ^ 2 = J ^ 1 2 + J ^ 2 2 + 2 ( J ^ 1 x J ^ 2 x + J ^ 1 y J ^ 2 y + J ^ 1 z J ^ 2 z ) \hat{J}^2 = (\hat{J}_1 + \hat{J}_2)^2 \ \ \ = \hat{J}1^2 + \hat{J}2^2 + 2 \hat{J}1 \cdot \hat{J}2 \ \ \ = \hat{J}1^2 + \hat{J}2^2 + 2 \left( \hat{J} {1x} \hat{J} {2x} + \hat{J} {1y} \hat{J} {2y} + \hat{J} {1z} \hat{J} {2z} \right) J ^ 2 = ( J ^ 1 + J ^ 2 ) 2 = J ^ 1 2 + J ^ 2 2 + 2 J ^ 1 ⋅ J ^ 2 = J ^ 1 2 + J ^ 2 2 + 2 ( J ^ 1 x J ^ 2 x + J ^ 1 y J ^ 2 y + J ^ 1 z J ^ 2 z )
可得
[ J ^ 2 , J ⃗ ^ 1 ] ≠ 0 , [ J ^ 2 , J ⃗ ^ 2 ] ≠ 0 [\hat{J}^2 , \hat{\vec{J}}_1] \ne 0 ,\kern 1em [\hat{J}^2 , \hat{\vec{J}}_2] \ne 0 [ J ^ 2 , J ^ 1 ] = 0 , [ J ^ 2 , J ^ 2 ] = 0
非耦合表象使用 ψ j 1 m 1 ( 1 ) ψ j 2 m 2 ( 2 ) \psi_{j_1m_1}(1)\psi_{j_2m_2}(2) ψ j 1 m 1 ( 1 ) ψ j 2 m 2 ( 2 ) 力学量完备集 为
{ J ^ 1 2 , J ^ 1 z , J ^ 2 2 , J ^ 2 z } { \hat{J}1^2 , \hat{J} {1z} , \hat{J}2^2 , \hat{J} {2z} } { J ^ 1 2 , J ^ 1 z , J ^ 2 2 , J ^ 2 z }
使用Dirac符号表示基底 为
∣ j 1 m 1 j 2 m 2 ⟩ = ∣ j 1 m 1 ⟩ ∣ j 2 m 2 ⟩ | j_1m_1j_2m_2 \rangle = | j_1m_1 \rangle | j_2m_2 \rangle ∣ j 1 m 1 j 2 m 2 ⟩ = ∣ j 1 m 1 ⟩ ∣ j 2 m 2 ⟩
对于确定的 j 1 , j 2 j_1 , j_2 j 1 , j 2 m 1 , m 2 m_1 , m_2 m 1 , m 2 维数 为
( 2 j 1 + 1 ) ( 2 j 2 + 1 ) (2j_1 + 1)(2j_2 + 1) ( 2 j 1 + 1 ) ( 2 j 2 + 1 )
封闭关系 为
∑ m 1 = − j 1 j 1 ∑ m 2 = − j 2 j 2 ∣ j 1 m 1 j 2 m 2 ⟩ ⟨ j 1 m 1 j 2 m 2 ∣ = I \sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} | j_1m_1j_2m_2 \rangle \langle j_1m_1j_2m_2 | = I m 1 = − j 1 ∑ j 1 m 2 = − j 2 ∑ j 2 ∣ j 1 m 1 j 2 m 2 ⟩ ⟨ j 1 m 1 j 2 m 2 ∣ = I
需要注意的是,在非耦合表象中, J ^ 1 2 , J ^ 1 z \hat{J}1^2 , \hat{J} {1z} J ^ 1 2 , J ^ 1 z ∣ j 1 m 1 ⟩ | j_1m_1 \rangle ∣ j 1 m 1 ⟩ J ^ 2 2 , J ^ 2 z \hat{J}2^2 , \hat{J} {2z} J ^ 2 2 , J ^ 2 z ∣ j 2 m 2 ⟩ | j_2m_2 \rangle ∣ j 2 m 2 ⟩
J ^ 1 2 ∣ j 1 m 1 j 2 m 2 ⟩ = j 1 ( j 1 + 1 ) ℏ 2 ∣ j 1 m 1 j 2 m 2 ⟩ J ^ 1 z ∣ j 1 m 1 j 2 m 2 ⟩ = m 1 ℏ ∣ j 1 m 1 j 2 m 2 ⟩ J ^ 2 2 ∣ j 1 m 1 j 2 m 2 ⟩ = j 2 ( j 2 + 1 ) ℏ 2 ∣ j 1 m 1 j 2 m 2 ⟩ J ^ 2 z ∣ j 1 m 1 j 2 m 2 ⟩ = m 2 ℏ ∣ j 1 m 1 j 2 m 2 ⟩ \hat{J}1^2\ | j_1m_1j_2m_2 \rangle = j_1(j_1+1)\hbar^2\ | j_1m_1j_2m_2 \rangle \ \ \ \hat{J} {1z}\ | j_1m_1j_2m_2 \rangle = m_1\hbar\ | j_1m_1j_2m_2 \rangle \ \ \ \hat{J}2^2\ | j_1m_1j_2m_2 \rangle = j_2(j_2+1)\hbar^2\ | j_1m_1j_2m_2 \rangle \ \ \ \hat{J} {2z}\ | j_1m_1j_2m_2 \rangle = m_2\hbar\ | j_1m_1j_2m_2 \rangle J ^ 1 2 ∣ j 1 m 1 j 2 m 2 ⟩ = j 1 ( j 1 + 1 ) ℏ 2 ∣ j 1 m 1 j 2 m 2 ⟩ J ^ 1 z ∣ j 1 m 1 j 2 m 2 ⟩ = m 1 ℏ ∣ j 1 m 1 j 2 m 2 ⟩ J ^ 2 2 ∣ j 1 m 1 j 2 m 2 ⟩ = j 2 ( j 2 + 1 ) ℏ 2 ∣ j 1 m 1 j 2 m 2 ⟩ J ^ 2 z ∣ j 1 m 1 j 2 m 2 ⟩ = m 2 ℏ ∣ j 1 m 1 j 2 m 2 ⟩
非耦合表象使用 ψ j 1 j 2 j m ( 1 , 2 ) \psi_{j_1j_2jm}(1,2) ψ j 1 j 2 jm ( 1 , 2 ) 力学量完备集 为
{ J ^ 1 2 , J ^ 2 2 , J ^ 2 , J ^ z } { \hat{J}1^2 , \hat{J} {2}^2 , \hat{J}^2 , \hat{J}_{z} } { J ^ 1 2 , J ^ 2 2 , J ^ 2 , J ^ z }
使用Dirac符号表示基底 为
∣ j 1 j 2 j m ⟩ | j_1j_2jm \rangle ∣ j 1 j 2 jm ⟩
封闭关系 为
∑ j = j min j max ∑ m = − j j ∣ j 1 j 2 j m ⟩ ⟨ j 1 j 2 j m ∣ = I \sum_{j=j_{\min}}^{j_{\max}} \sum_{m=-j}^{j} | j_1j_2jm \rangle \langle j_1j_2jm | = I j = j m i n ∑ j m a x m = − j ∑ j ∣ j 1 j 2 jm ⟩ ⟨ j 1 j 2 jm ∣ = I
在耦合表象中,算符对态的作用为
J ^ 1 2 ∣ j 1 j 2 j m ⟩ = j 1 ( j 1 + 1 ) ℏ 2 ∣ j 1 j 2 j m ⟩ J ^ 2 2 ∣ j 1 j 2 j m ⟩ = j 2 ( j 2 + 1 ) ℏ 2 ∣ j 1 j 2 j m ⟩ J ^ 2 ∣ j 1 j 2 j m ⟩ = j ( j + 1 ) ℏ 2 ∣ j 1 j 2 j m ⟩ J ^ z ∣ j 1 j 2 j m ⟩ = m ℏ ∣ j 1 j 2 j m ⟩ \hat{J}_1^2\ | j_1j_2jm \rangle = j_1(j_1+1)\hbar^2\ | j_1j_2jm \rangle \ \ \ \hat{J}2^2\ | j_1j_2jm \rangle = j_2(j_2+1)\hbar^2\ | j_1j_2jm \rangle \ \ \ \hat{J}^2\ | j_1j_2jm \rangle = j(j+1)\hbar^2\ | j_1j_2jm \rangle \ \ \ \hat{J} {z}\ | j_1j_2jm \rangle = m\hbar\ | j_1j_2jm \rangle J ^ 1 2 ∣ j 1 j 2 jm ⟩ = j 1 ( j 1 + 1 ) ℏ 2 ∣ j 1 j 2 jm ⟩ J ^ 2 2 ∣ j 1 j 2 jm ⟩ = j 2 ( j 2 + 1 ) ℏ 2 ∣ j 1 j 2 jm ⟩ J ^ 2 ∣ j 1 j 2 jm ⟩ = j ( j + 1 ) ℏ 2 ∣ j 1 j 2 jm ⟩ J ^ z ∣ j 1 j 2 jm ⟩ = m ℏ ∣ j 1 j 2 jm ⟩
对于确定的 j 1 , j 2 j_1,j_2 j 1 , j 2 ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) (2j_1+1)(2j_2+1) ( 2 j 1 + 1 ) ( 2 j 2 + 1 )
∣ j 1 j 2 j m ⟩ = ∑ m 1 = − j 1 j 1 ∑ m 2 = − j 2 j 2 ∣ j 1 m 1 j 2 m 2 ⟩ ⟨ j 1 m 1 j 2 m 2 ∣ j 1 j 2 j m ⟩ | j_1j_2jm \rangle = \sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} | j_1m_1j_2m_2 \rangle \langle j_1m_1j_2m_2 | j_1j_2jm \rangle ∣ j 1 j 2 jm ⟩ = m 1 = − j 1 ∑ j 1 m 2 = − j 2 ∑ j 2 ∣ j 1 m 1 j 2 m 2 ⟩ ⟨ j 1 m 1 j 2 m 2 ∣ j 1 j 2 jm ⟩
其中的展开系数称为Clebsch-Gordan(CG)系数 ,记为
C j 1 m 1 j 2 m 2 j m = ⟨ j 1 m 1 j 2 m 2 ∣ j 1 j 2 j m ⟩ C_{j_1m_1j_2m_2}^{jm} = \langle j_1m_1j_2m_2 | j_1j_2jm \rangle C j 1 m 1 j 2 m 2 jm = ⟨ j 1 m 1 j 2 m 2 ∣ j 1 j 2 jm ⟩
总角动量 { J ^ 2 , J ^ z } { \hat{J}^2 , \hat{J}_z } { J ^ 2 , J ^ z } ∣ j m ⟩ | jm \rangle ∣ jm ⟩ j 1 , j 2 j_1,j_2 j 1 , j 2 总角量子数 j j j
j = ∣ j 1 − j 2 ∣ , ∣ j 1 − j 2 ∣ + 1 , ⋯ , j 1 + j 2 − 1 , j 1 + j 2 j = |j_1-j_2|\ ,\ |j_1-j_2|+1\ ,\ \cdots ,\ j_1+j_2-1\ ,\ j_1+j_2 j = ∣ j 1 − j 2 ∣ , ∣ j 1 − j 2 ∣ + 1 , ⋯ , j 1 + j 2 − 1 , j 1 + j 2
首先,根据非耦合表象向耦合表象的基底变换,可得
J ^ z ∣ j 1 j 2 j m ⟩ = m ℏ ∣ j 1 j 2 j m ⟩ = ∑ m 1 = − j 1 j 1 ∑ m 2 = − j 2 j 2 m ℏ C j 1 m 1 j 2 m 2 j m ∣ j 1 m 1 j 2 m 2 ⟩ \hat{J}z\ | j_1j_2jm \rangle = m\hbar\ | j_1j_2jm \rangle = \sum {m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} m\hbar\ C_{j_1m_1j_2m_2}^{jm} | j_1m_1j_2m_2 \rangle J ^ z ∣ j 1 j 2 jm ⟩ = m ℏ ∣ j 1 j 2 jm ⟩ = m 1 = − j 1 ∑ j 1 m 2 = − j 2 ∑ j 2 m ℏ C j 1 m 1 j 2 m 2 jm ∣ j 1 m 1 j 2 m 2 ⟩
而根据 J ^ z = J ^ 1 z + J ^ 2 z \hat{J}z = \hat{J} {1z} + \hat{J}_{2z} J ^ z = J ^ 1 z + J ^ 2 z
J ^ z ∣ j 1 j 2 j m ⟩ = ( J ^ 1 z + J ^ 2 z ) ∣ j 1 j 2 j m ⟩ = ( J ^ 1 z + J ^ 2 z ) ∑ m 1 = − j 1 j 1 ∑ m 2 = − j 2 j 2 C j 1 m 1 j 2 m 2 j m ∣ j 1 m 1 j 2 m 2 ⟩ = ∑ m 1 = − j 1 j 1 ∑ m 2 = − j 2 j 2 ( m 1 + m 2 ) ℏ C j 1 m 1 j 2 m 2 j m ∣ j 1 m 1 j 2 m 2 ⟩ \hat{J}z\ | j_1j_2jm \rangle = (\hat{J} {1z} + \hat{J}{2z}) | j_1j_2jm \rangle \ \ \ = (\hat{J} {1z} + \hat{J}{2z}) \sum {m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} C_{j_1m_1j_2m_2}^{jm} | j_1m_1j_2m_2 \rangle \ \ \ = \sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} (m_1+m_2)\hbar\ C_{j_1m_1j_2m_2}^{jm} | j_1m_1j_2m_2 \rangle J ^ z ∣ j 1 j 2 jm ⟩ = ( J ^ 1 z + J ^ 2 z ) ∣ j 1 j 2 jm ⟩ = ( J ^ 1 z + J ^ 2 z ) m 1 = − j 1 ∑ j 1 m 2 = − j 2 ∑ j 2 C j 1 m 1 j 2 m 2 jm ∣ j 1 m 1 j 2 m 2 ⟩ = m 1 = − j 1 ∑ j 1 m 2 = − j 2 ∑ j 2 ( m 1 + m 2 ) ℏ C j 1 m 1 j 2 m 2 jm ∣ j 1 m 1 j 2 m 2 ⟩
两式对比,可得
∑ m 1 = − j 1 j 1 ∑ m 2 = − j 2 j 2 ( m − m 1 − m 2 ) ℏ C j 1 m 1 j 2 m 2 j m ∣ j 1 m 1 j 2 m 2 ⟩ = 0 \sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} (m-m_1-m_2)\hbar\ C_{j_1m_1j_2m_2}^{jm} | j_1m_1j_2m_2 \rangle = 0 m 1 = − j 1 ∑ j 1 m 2 = − j 2 ∑ j 2 ( m − m 1 − m 2 ) ℏ C j 1 m 1 j 2 m 2 jm ∣ j 1 m 1 j 2 m 2 ⟩ = 0
由于基矢 ∣ j 1 m 1 j 2 m 2 ⟩ | j_1m_1j_2m_2 \rangle ∣ j 1 m 1 j 2 m 2 ⟩
m = m 1 + m 2 m = m_1 + m_2 m = m 1 + m 2
考虑到 m 1 , m 2 m_1,m_2 m 1 , m 2
m 1 = − j 1 , − j 1 + 1 , ⋯ , j 1 − 1 , j 1 m 2 = − j 2 , − j 2 + 1 , ⋯ , j 2 − 1 , j 2 m_1 = -j_1\ ,\ -j_1+1\ , \cdots ,\ j_1-1\ ,\ j_1 \ m_2 = -j_2\ ,\ -j_2+1\ , \cdots ,\ j_2-1\ ,\ j_2 m 1 = − j 1 , − j 1 + 1 , ⋯ , j 1 − 1 , j 1 m 2 = − j 2 , − j 2 + 1 , ⋯ , j 2 − 1 , j 2
故可得 m m m
m max = ( m 1 + m 2 ) max = j 1 + j 2 m_{\max} = (m_1 + m_2)_{\max} = j_1 + j_2 m m a x = ( m 1 + m 2 ) m a x = j 1 + j 2
而 m m m − j -j − j j j j
j max = m max = j 1 + j 2 j_{\max} = m_{\max} = j_1 + j_2 j m a x = m m a x = j 1 + j 2
值得注意的是 j min j_{\min} j m i n m m m j j j 2 j + 1 2j+1 2 j + 1
∑ j = j min j 1 + j 2 ( 2 j + 1 ) = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ 1 2 ( j 1 + j 2 − j min + 1 ) [ ( 2 j min + 1 ) + ( 2 j 1 + 2 j 2 + 1 ) ] = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ ( j 1 + j 2 − j min + 1 ) ( j min + j 1 + j 2 + 1 ) = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ ( j 1 + j 2 + 1 ) 2 − j min 2 = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ j min 2 = ( j 1 − j 2 ) 2 ⇓ j min = ∣ j 1 − j 2 ∣ \sum_{j=j_{\min}}^{j_1+j_2} (2j+1) = (2j_1+1)(2j_2+1) \ \Downarrow \ \frac12(j_1+j_2-j_{\min}+1)[(2j_{\min}+1)+(2j_1+2j_2+1)] = (2j_1+1)(2j_2+1) \ \Downarrow \ (j_1+j_2-j_{\min}+1)(j_{\min}+j_1+j_2+1) = (2j_1+1)(2j_2+1) \ \Downarrow \ (j_1+j_2+1)^2 - j_{\min}^2 = (2j_1+1)(2j_2+1) \ \Downarrow \ j_{\min}^2 = (j_1-j_2)^2 \ \Downarrow \ j_{\min} = |j_1-j_2| j = j m i n ∑ j 1 + j 2 ( 2 j + 1 ) = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ 2 1 ( j 1 + j 2 − j m i n + 1 ) [( 2 j m i n + 1 ) + ( 2 j 1 + 2 j 2 + 1 )] = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ ( j 1 + j 2 − j m i n + 1 ) ( j m i n + j 1 + j 2 + 1 ) = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ ( j 1 + j 2 + 1 ) 2 − j m i n 2 = ( 2 j 1 + 1 ) ( 2 j 2 + 1 ) ⇓ j m i n 2 = ( j 1 − j 2 ) 2 ⇓ j m i n = ∣ j 1 − j 2 ∣
J ⃗ ^ 1 ⋅ J ⃗ ^ 2 = 1 2 ( J ^ 2 − J ^ 1 2 − J ^ 2 2 ) \hat{\vec{J}}_1 \cdot \hat{\vec{J}}_2 = \frac12 \left( \hat{J}^2 - \hat{J}_1^2 - \hat{J}_2^2 \right) J ^ 1 ⋅ J ^ 2 = 2 1 ( J ^ 2 − J ^ 1 2 − J ^ 2 2 )
两电子体系的自旋自由度为 2 2 2 { S ^ 1 2 , S ^ 1 z , S ^ 2 2 , S ^ 2 z } { \hat{S}1^2 , \hat{S} {1z} , \hat{S}2^2 , \hat{S} {2z} } { S ^ 1 2 , S ^ 1 z , S ^ 2 2 , S ^ 2 z } { S ^ 1 2 , S ^ 2 2 , S ^ 2 , S ^ z } { \hat{S}_1^2 , \hat{S}2^2 , \hat{S}^2 , \hat{S} {z} } { S ^ 1 2 , S ^ 2 2 , S ^ 2 , S ^ z }
对于电子,由于 S ^ 1 2 , S ^ 2 2 \hat{S}_1^2 , \hat{S}_2^2 S ^ 1 2 , S ^ 2 2 3 4 ℏ 2 \frac34\hbar^2 4 3 ℏ 2 S ^ 1 2 , S ^ 2 2 \hat{S}_1^2 , \hat{S}_2^2 S ^ 1 2 , S ^ 2 2
在单体近似下,忽略两个电子间的 S − S S-S S − S χ ( S 1 z , S 2 z ) \chi(S_{1z},S_{2z}) χ ( S 1 z , S 2 z ) χ m s ( S k z ) \chi_{m_s}(S_{kz}) χ m s ( S k z )
χ ( S 1 z , S 2 z ) = χ m s ( S 1 z ) χ m s ′ ( S 2 z ) \chi(S_{1z},S_{2z}) = \chi_{m_s}(S_{1z})\ \chi_{m_s'}(S_{2z}) χ ( S 1 z , S 2 z ) = χ m s ( S 1 z ) χ m s ′ ( S 2 z )
其中自旋量子数 s 1 = s 2 = 1 2 s_1 = s_2 = \frac12 s 1 = s 2 = 2 1 m s = ± 1 2 , m s ′ = ± 1 2 m_s = \pm\frac12 , m_s' = \pm\frac12 m s = ± 2 1 , m s ′ = ± 2 1
χ ( 1 ) = ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 = χ 1 / 2 ( S 1 z ) χ 1 / 2 ( S 2 z ) χ ( 2 ) = ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 = χ − 1 / 2 ( S 1 z ) χ − 1 / 2 ( S 2 z ) χ ( 3 ) = ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 = χ 1 / 2 ( S 1 z ) χ − 1 / 2 ( S 2 z ) χ ( 4 ) = ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 = χ − 1 / 2 ( S 1 z ) χ 1 / 2 ( S 2 z ) \chi^{(1)} = |\uparrow\ \rangle_1 |\uparrow\ \rangle_2 = \chi_{1/2}(S_{1z})\ \chi_{1/2}(S_{2z}) \ \ \ \chi^{(2)} = |\downarrow\ \rangle_1 |\downarrow\ \rangle_2 = \chi_{-1/2}(S_{1z})\ \chi_{-1/2}(S_{2z}) \ \ \ \chi^{(3)} = |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 = \chi_{1/2}(S_{1z})\ \chi_{-1/2}(S_{2z}) \ \ \ \chi^{(4)} = |\downarrow\ \rangle_1 |\uparrow\ \rangle_2 = \chi_{-1/2}(S_{1z})\ \chi_{1/2}(S_{2z}) χ ( 1 ) = ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 = χ 1/2 ( S 1 z ) χ 1/2 ( S 2 z ) χ ( 2 ) = ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 = χ − 1/2 ( S 1 z ) χ − 1/2 ( S 2 z ) χ ( 3 ) = ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 = χ 1/2 ( S 1 z ) χ − 1/2 ( S 2 z ) χ ( 4 ) = ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 = χ − 1/2 ( S 1 z ) χ 1/2 ( S 2 z )
其中的 ∣ ↑ ⟩ 1 |\uparrow\ \rangle_1 ∣ ↑ ⟩ 1 ∣ ↑ ↑ ⟩ 12 |\uparrow\ \uparrow\ \rangle_{12} ∣ ↑ ↑ ⟩ 12
在耦合表象中,基底为
χ 00 = 1 2 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 − ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] χ 10 = 1 2 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 + ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] χ 11 = ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 χ 1 , − 1 = ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 \chi_{00} = \frac{1}{\sqrt{2}} \left[\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 - |\downarrow\ \rangle_1 |\uparrow\ \rangle_2\ \right] \ \ \ \chi_{10} = \frac{1}{\sqrt{2}} \left[\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 + |\downarrow\ \rangle_1 |\uparrow\ \rangle_2\ \right] \ \ \ \chi_{11} = |\uparrow\ \rangle_1 |\uparrow\ \rangle_2 \ \ \ \chi_{1,-1} = |\downarrow\ \rangle_1 |\downarrow\ \rangle_2 χ 00 = 2 1 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 − ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] χ 10 = 2 1 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 + ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] χ 11 = ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 χ 1 , − 1 = ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2
对应的本征值与交换对称性如表所示
态 交换对称性 S ^ 2 \hat{S}^2 S ^ 2 S ^ z \hat{S}_z S ^ z
χ 00 \chi_{00} χ 00 反对称 0 0 0 0 0 0 χ 10 \chi_{10} χ 10 对称 2 ℏ 2 2\hbar^2 2 ℏ 2 0 0 0 χ 11 \chi_{11} χ 11 对称 2 ℏ 2 2\hbar^2 2 ℏ 2 ℏ \hbar ℏ χ 1 , − 1 \chi_{1,-1} χ 1 , − 1 对称 2 ℏ 2 2\hbar^2 2 ℏ 2 − ℏ -\hbar − ℏ
其中:自旋总量子数 s = 1 s=1 s = 1 χ 10 , χ 11 , χ 1 , − 1 \chi_{10},\chi_{11},\chi_{1,-1} χ 10 , χ 11 , χ 1 , − 1 自旋三重态 ;自旋总量子数 s = 0 s=0 s = 0 χ 00 \chi_{00} χ 00 自旋单态 。
电子为Fermi子,多电子体系的总波函数应该是交换反对称的,故若自旋波函数为交换对称的,则空间波函数当为自旋反对称的,而若自旋波函数为交换反对称的,则空间波函数当为自旋对称的。
在非耦合表象的基底中,可以验证四个态均为 S z S_z S z S ^ z = S ^ 1 z + S ^ 2 z \hat{S}{z} = \hat{S} {1z} + \hat{S}_{2z} S ^ z = S ^ 1 z + S ^ 2 z
S ^ k z ∣ ↑ ⟩ k = 1 2 ℏ ∣ ↑ ⟩ k S ^ k z ∣ ↓ ⟩ k = − 1 2 ℏ ∣ ↓ ⟩ k \hat{S}{kz} |\uparrow\ \rangle_k = \frac12\hbar\ |\uparrow\ \rangle_k \ \ \ \hat{S} {kz} |\downarrow\ \rangle_k = -\frac12\hbar\ |\downarrow\ \rangle_k S ^ k z ∣ ↑ ⟩ k = 2 1 ℏ ∣ ↑ ⟩ k S ^ k z ∣ ↓ ⟩ k = − 2 1 ℏ ∣ ↓ ⟩ k
容易得到
S ^ z ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 = ℏ ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 S ^ z ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 = − ℏ ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 S ^ z ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 = 0 ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 S ^ z ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 = 0 ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 \hat{S}_z\ |\uparrow\ \rangle_1 |\uparrow\ \rangle_2 = \hbar\ |\uparrow\ \rangle_1 |\uparrow\ \rangle_2 \ \ \ \hat{S}_z\ |\downarrow\ \rangle_1 |\downarrow\ \rangle_2 = -\hbar\ |\downarrow\ \rangle_1 |\downarrow\ \rangle_2 \ \ \ \hat{S}_z\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 = 0\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 \ \ \ \hat{S}_z\ |\downarrow\ \rangle_1 |\uparrow\ \rangle_2 = 0\ |\downarrow\ \rangle_1 |\uparrow\ \rangle_2 S ^ z ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 = ℏ ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 S ^ z ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 = − ℏ ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 S ^ z ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 = 0 ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 S ^ z ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 = 0 ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2
同时,根据
S ^ 2 = ( S ⃗ ^ 1 + S ⃗ ^ 2 ) 2 = S ^ 1 2 + S ^ 2 2 + 2 S ⃗ ^ 1 ⋅ S ⃗ ^ 2 = 3 2 ℏ 2 + 2 ( S ^ 1 x S ^ 2 x + S ^ 1 y S ^ 2 y + S ^ 1 z S ^ 2 z ) \hat{S}^2 = (\hat{\vec{S}}1 + \hat{\vec{S}}2)^2 \ \ \ = \hat{S}1^2 + \hat{S}2^2 + 2 \hat{\vec{S}}1 \cdot \hat{\vec{S}}2 \ \ \ = \frac32 \hbar^2 + 2 \left( \hat{S} {1x}\hat{S} {2x} + \hat{S} {1y}\hat{S} {2y} + \hat{S} {1z}\hat{S} {2z}\right) S ^ 2 = ( S ^ 1 + S ^ 2 ) 2 = S ^ 1 2 + S ^ 2 2 + 2 S ^ 1 ⋅ S ^ 2 = 2 3 ℏ 2 + 2 ( S ^ 1 x S ^ 2 x + S ^ 1 y S ^ 2 y + S ^ 1 z S ^ 2 z )
以及
S ^ x ∣ ↑ ⟩ = ℏ 2 [ 0 1 1 0 ] [ 1 0 ] = ℏ 2 [ 0 1 ] = ℏ 2 ∣ ↓ ⟩ S ^ x ∣ ↓ ⟩ = ℏ 2 [ 0 1 1 0 ] [ 0 1 ] = ℏ 2 [ 1 0 ] = ℏ 2 ∣ ↑ ⟩ S ^ y ∣ ↑ ⟩ = ℏ 2 [ 0 − i i 0 ] [ 1 0 ] = i ℏ 2 [ 0 1 ] = i ℏ 2 ∣ ↓ ⟩ S ^ y ∣ ↓ ⟩ = ℏ 2 [ 0 − i i 0 ] [ 0 1 ] = − i ℏ 2 [ 1 0 ] = − i ℏ 2 ∣ ↑ ⟩ \hat{S}_x\ |\uparrow\ \rangle = \frac{\hbar}{2} \begin{bmatrix} 0 & 1 \ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \ 0 \end{bmatrix} = \frac{\hbar}{2} \begin{bmatrix} 0 \ 1 \end{bmatrix} = \frac{\hbar}{2}\ |\downarrow\ \rangle \ \ \ \hat{S}_x\ |\downarrow\ \rangle = \frac{\hbar}{2} \begin{bmatrix} 0 & 1 \ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 \ 1 \end{bmatrix} = \frac{\hbar}{2} \begin{bmatrix} 1 \ 0 \end{bmatrix} = \frac{\hbar}{2}\ |\uparrow\ \rangle \ \ \ \hat{S}_y\ |\uparrow\ \rangle = \frac{\hbar}{2} \begin{bmatrix} 0 & -\mathrm{i} \ \mathrm{i} & 0 \end{bmatrix} \begin{bmatrix} 1 \ 0 \end{bmatrix} = \frac{\mathrm{i}\hbar}{2} \begin{bmatrix} 0 \ 1 \end{bmatrix} = \frac{\mathrm{i}\hbar}{2}\ |\downarrow\ \rangle \ \ \ \hat{S}_y\ |\downarrow\ \rangle = \frac{\hbar}{2} \begin{bmatrix} 0 & -\mathrm{i} \ \mathrm{i} & 0 \end{bmatrix} \begin{bmatrix} 0 \ 1 \end{bmatrix} = -\frac{\mathrm{i}\hbar}{2} \begin{bmatrix} 1 \ 0 \end{bmatrix} = -\frac{\mathrm{i}\hbar}{2}\ |\uparrow\ \rangle S ^ x ∣ ↑ ⟩ = 2 ℏ [ 0 1 1 0 ] [ 1 0 ] = 2 ℏ [ 0 1 ] = 2 ℏ ∣ ↓ ⟩ S ^ x ∣ ↓ ⟩ = 2 ℏ [ 0 1 1 0 ] [ 0 1 ] = 2 ℏ [ 1 0 ] = 2 ℏ ∣ ↑ ⟩ S ^ y ∣ ↑ ⟩ = 2 ℏ [ 0 i − i 0 ] [ 1 0 ] = 2 i ℏ [ 0 1 ] = 2 i ℏ ∣ ↓ ⟩ S ^ y ∣ ↓ ⟩ = 2 ℏ [ 0 i − i 0 ] [ 0 1 ] = − 2 i ℏ [ 1 0 ] = − 2 i ℏ ∣ ↑ ⟩
可得 ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 |\uparrow\ \rangle_1 |\uparrow\ \rangle_2 ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 |\downarrow\ \rangle_1 |\downarrow\ \rangle_2 ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 S ^ 2 \hat{S}^2 S ^ 2
S ^ 2 ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 = 2 ℏ 2 ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 S ^ 2 ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 = 2 ℏ 2 ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 \hat{S}^2\ |\uparrow\ \rangle_1 |\uparrow\ \rangle_2 = 2\hbar^2\ |\uparrow\ \rangle_1 |\uparrow\ \rangle_2 \ \ \ \hat{S}^2\ |\downarrow\ \rangle_1 |\downarrow\ \rangle_2 = 2\hbar^2\ |\downarrow\ \rangle_1 |\downarrow\ \rangle_2 S ^ 2 ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 = 2 ℏ 2 ∣ ↑ ⟩ 1 ∣ ↑ ⟩ 2 S ^ 2 ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2 = 2 ℏ 2 ∣ ↓ ⟩ 1 ∣ ↓ ⟩ 2
根据对应的本征值(量子数),将这两个态记为 χ 11 \chi_{11} χ 11 χ 1 , − 1 \chi_{1,-1} χ 1 , − 1 ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 |\downarrow\ \rangle_1 |\uparrow\ \rangle_2 ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 S ^ 2 \hat{S}^2 S ^ 2 S ^ 2 \hat{S}^2 S ^ 2
S ^ 2 1 2 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 − ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] = 0 × 1 2 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 − ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] S ^ 2 1 2 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 + ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] = 2 ℏ 2 1 2 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 + ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] \hat{S}^2 \frac{1}{\sqrt{2}} \left[\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 - |\downarrow\ \rangle_1 |\uparrow\ \rangle_2\ \right] = 0 \times \frac{1}{\sqrt{2}} \left[\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 - |\downarrow\ \rangle_1 |\uparrow\ \rangle_2\ \right] \ \ \ \hat{S}^2 \frac{1}{\sqrt{2}} \left[\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 + |\downarrow\ \rangle_1 |\uparrow\ \rangle_2\ \right] = 2\hbar^2\ \frac{1}{\sqrt{2}} \left[\ |\uparrow\ \rangle_1 |\downarrow\ \rangle_2 + |\downarrow\ \rangle_1 |\uparrow\ \rangle_2\ \right] S ^ 2 2 1 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 − ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] = 0 × 2 1 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 − ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] S ^ 2 2 1 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 + ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ] = 2 ℏ 2 2 1 [ ∣ ↑ ⟩ 1 ∣ ↓ ⟩ 2 + ∣ ↓ ⟩ 1 ∣ ↑ ⟩ 2 ]
根据对应的本征值(量子数),将这两个态记为 χ 00 \chi_{00} χ 00 χ 10 \chi_{10} χ 10
设体系的Hamilton量为 H ^ \hat{H} H ^ t t t
H ^ ψ = E ψ \hat{H} \psi = E \psi H ^ ψ = E ψ
此方程求解一般比较困难,可以采用微扰论 求解能量本征值与本征态的近似值。假设
H ^ = H ^ 0 + H ^ ′ \hat{H} = \hat{H}_0 + \hat{H}' H ^ = H ^ 0 + H ^ ′
其中 H ^ 0 \hat{H}_0 H ^ 0 H ^ ′ \hat{H}' H ^ ′ H ^ 0 \hat{H}_0 H ^ 0 H ^ ′ ≪ H ^ 0 \hat{H}' \ll \hat{H}_0 H ^ ′ ≪ H ^ 0 微扰 ,可以在 H ^ 0 \hat{H}_0 H ^ 0 H ^ ′ \hat{H}' H ^ ′
将能量本征值与本征态逐级展开,即
ψ n = ∑ s = 0 + ∞ ψ n ( s ) = ψ n ( 0 ) + ψ n ( 1 ) + ψ n ( 2 ) + ⋯ E n = ∑ s = 0 + ∞ E n ( s ) = E n ( 0 ) + E n ( 1 ) + E n ( 2 ) + ⋯ \psi_n = \sum_{s=0}^{+\infty} \psi_n^{(s)} = \psi_n^{(0)} + \psi_n^{(1)} + \psi_n^{(2)} + \cdots \ \ \ E_n = \sum_{s=0}^{+\infty} E_n^{(s)} = E_n^{(0)} + E_n^{(1)} + E_n^{(2)} + \cdots ψ n = s = 0 ∑ + ∞ ψ n ( s ) = ψ n ( 0 ) + ψ n ( 1 ) + ψ n ( 2 ) + ⋯ E n = s = 0 ∑ + ∞ E n ( s ) = E n ( 0 ) + E n ( 1 ) + E n ( 2 ) + ⋯
其中 H ^ 0 ψ n ( 0 ) = E n ( 0 ) ψ n ( 0 ) \hat{H}_0 \psi_n^{(0)} = E_n^{(0)} \psi_n^{(0)} H ^ 0 ψ n ( 0 ) = E n ( 0 ) ψ n ( 0 ) E n ( s ) E_n^{(s)} E n ( s ) ψ n ( s ) \psi_n^{(s)} ψ n ( s ) H ^ ′ \hat{H}' H ^ ′ s s s s > 0 s>0 s > 0 波函数的各级高级近似解与零级近似解都正交 ,即
⟨ ψ n ( 0 ) ∣ ψ n ( s ) ⟩ = 0 ( s = 1 , 2 , 3 , ⋯ ) \langle \psi_n^{(0)} | \psi_n^{(s)} \rangle = 0 \kern 2em (s=1,2,3,\cdots) ⟨ ψ n ( 0 ) ∣ ψ n ( s ) ⟩ = 0 ( s = 1 , 2 , 3 , ⋯ )
将能量本征值与本征态的展开式代入原能量本征方程,即
( H ^ 0 + H ^ ′ ) ( ψ n ( 0 ) + ψ n ( 1 ) + ψ n ( 2 ) + ⋯ ) = ( E n ( 0 ) + E n ( 1 ) + E n ( 2 ) + ⋯ ) ( ψ n ( 0 ) + ψ n ( 1 ) + ψ n ( 2 ) + ⋯ ) \left( \hat{H}_0 + \hat{H}' \right) \left( \psi_n^{(0)} + \psi_n^{(1)} + \psi_n^{(2)} + \cdots \right) = \left( E_n^{(0)} + E_n^{(1)} + E_n^{(2)} + \cdots \right) \left( \psi_n^{(0)} + \psi_n^{(1)} + \psi_n^{(2)} + \cdots \right) ( H ^ 0 + H ^ ′ ) ( ψ n ( 0 ) + ψ n ( 1 ) + ψ n ( 2 ) + ⋯ ) = ( E n ( 0 ) + E n ( 1 ) + E n ( 2 ) + ⋯ ) ( ψ n ( 0 ) + ψ n ( 1 ) + ψ n ( 2 ) + ⋯ )
比较等式两边的同级项,可得出各级近似下的能量本征方程
( H ^ 0 − E n ( 0 ) ) ψ n ( 0 ) = 0 ( H ^ 0 − E n ( 0 ) ) ψ n ( 1 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ( H ^ 0 − E n ( 0 ) ) ψ n ( 2 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 1 ) + E n ( 2 ) ψ n ( 0 ) ( H ^ 0 − E n ( 0 ) ) ψ n ( 3 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 2 ) + E n ( 2 ) ψ n ( 1 ) + E n ( 3 ) ψ n ( 0 ) ⋯ \left( \hat{H}_0 - E_n^{(0)} \right) \psi_n^{(0)} = 0 \ \ \ \left( \hat{H}_0 - E_n^{(0)} \right) \psi_n^{(1)} = \left( E_n^{(1)} - \hat{H}' \right) \psi_n^{(0)} \ \ \ \left( \hat{H}_0 - E_n^{(0)} \right) \psi_n^{(2)} = \left( E_n^{(1)} - \hat{H}' \right) \psi_n^{(1)} + E_n^{(2)} \psi_n^{(0)} \ \ \ \left( \hat{H}_0 - E_n^{(0)} \right) \psi_n^{(3)} = \left( E_n^{(1)} - \hat{H}' \right) \psi_n^{(2)} + E_n^{(2)} \psi_n^{(1)} + E_n^{(3)} \psi_n^{(0)} \ \cdots ( H ^ 0 − E n ( 0 ) ) ψ n ( 0 ) = 0 ( H ^ 0 − E n ( 0 ) ) ψ n ( 1 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ( H ^ 0 − E n ( 0 ) ) ψ n ( 2 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 1 ) + E n ( 2 ) ψ n ( 0 ) ( H ^ 0 − E n ( 0 ) ) ψ n ( 3 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 2 ) + E n ( 2 ) ψ n ( 1 ) + E n ( 3 ) ψ n ( 0 ) ⋯
依次称为零级方程、一级方程、二级方程……逐级求解,即可得到各级近似解。
若在不考虑微扰时,体系处于非简并能级,即 H ^ 0 \hat{H}_0 H ^ 0 E n ( 0 ) E_n^{(0)} E n ( 0 ) ψ n ( 0 ) \psi_n^{(0)} ψ n ( 0 ) H ^ ′ \hat{H}' H ^ ′ { ψ n ( 0 ) } {\psi_n^{(0)}} { ψ n ( 0 ) }
H m n ′ = ⟨ ψ m ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ H'_{mn} = \langle \psi_m^{(0)} | \hat{H}' | \psi_n^{(0)} \rangle H mn ′ = ⟨ ψ m ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩
一级微扰能
E n ( 1 ) = H n n ′ = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ E_n^{(1)} = H'_{nn} = \langle \psi_n^{(0)} | \hat{H}' | \psi_n^{(0)} \rangle E n ( 1 ) = H nn ′ = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩
一级微扰波函数
ψ n ( 1 ) = ∑ m ≠ n H m n ′ E n ( 0 ) − E m ( 0 ) ψ m ( 0 ) \psi_n^{(1)} = \sum_{m \ne n} \frac{H'_{mn}}{E_n^{(0)}-E_m^{(0)}} \psi_m^{(0)} ψ n ( 1 ) = m = n ∑ E n ( 0 ) − E m ( 0 ) H mn ′ ψ m ( 0 )
二级微扰能
E n ( 2 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 1 ) ⟩ = ∑ m ≠ n ∣ H m n ′ ∣ 2 E n ( 0 ) − E m ( 0 ) E_n^{(2)} = \langle \psi_n^{(0)} | \hat{H}' | \psi_n^{(1)} \rangle = \sum_{m \ne n} \frac{\left|H'_{mn}\right|^2}{E_n^{(0)}-E_m^{(0)}} E n ( 2 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 1 ) ⟩ = m = n ∑ E n ( 0 ) − E m ( 0 ) ∣ H mn ′ ∣ 2
故准确到二级近似 的能量本征值 为
E n = E n ( 0 ) + H n n ′ + ∑ m ≠ n ∣ H m n ′ ∣ 2 E n ( 0 ) − E m ( 0 ) E_n = E_n^{(0)} + H'{nn} + \sum {m \ne n} \frac{\left|H'_{mn}\right|^2}{E_n^{(0)}-E_m^{(0)}} E n = E n ( 0 ) + H nn ′ + m = n ∑ E n ( 0 ) − E m ( 0 ) ∣ H mn ′ ∣ 2
准确到一级近似 的本征函数 为
ψ n = ψ n ( 0 ) + ∑ m ≠ n H m n ′ E n ( 0 ) − E m ( 0 ) ψ m ( 0 ) \psi_n = \psi_n^{(0)} + \sum_{m \ne n} \frac{H'_{mn}}{E_n^{(0)}-E_m^{(0)}} \psi_m^{(0)} ψ n = ψ n ( 0 ) + m = n ∑ E n ( 0 ) − E m ( 0 ) H mn ′ ψ m ( 0 )
非简并态微扰论的适用条件 为
∣ H m n ′ E n ( 0 ) − E m ( 0 ) ∣ ≪ 1 ( m ≠ n ) \left| \frac{H'_{mn}}{E_n^{(0)}-E_m^{(0)}} \right| \ll 1 \kern 2em (m \ne n) E n ( 0 ) − E m ( 0 ) H mn ′ ≪ 1 ( m = n )
故对于连续谱 ( ∣ E n ( 0 ) − E m ( 0 ) ∣ → 0 | E_n^{(0)} - E_m^{(0)} | \to 0 ∣ E n ( 0 ) − E m ( 0 ) ∣ → 0 非简并态 均不能使用 。
设一级微扰近似波函数表示为
ψ n ( 1 ) = ∑ m a m n ( 1 ) ψ m ( 0 ) \psi_n^{(1)} = \sum_m a_{mn}^{(1)} \psi_m^{(0)} ψ n ( 1 ) = m ∑ a mn ( 1 ) ψ m ( 0 )
代入一级方程,结合 { ψ n ( 0 ) } {\psi_n^{(0)}} { ψ n ( 0 ) }
( H ^ 0 − E n ( 0 ) ) ∑ m a m n ( 1 ) ψ m ( 0 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ⇓ ∑ m a m n ( 1 ) ( H ^ 0 − E n ( 0 ) ) ψ m ( 0 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ⇓ ∑ m a m n ( 1 ) ( E m ( 0 ) − E n ( 0 ) ) ψ m ( 0 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ⇓ ∑ m a m n ( 1 ) ⟨ ψ k ( 0 ) ∣ E m ( 0 ) − E n ( 0 ) ∣ ψ m ( 0 ) ⟩ = ⟨ ψ k ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 0 ) ⟩ ⇓ a k n ( 1 ) ( E k ( 0 ) − E n ( 0 ) ) = E n ( 1 ) δ k n − ⟨ ψ k ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ \left( \hat{H}0 - E_n^{(0)} \right) \sum_m a {mn}^{(1)} \psi_m^{(0)} = \left( E_n^{(1)} - \hat{H}' \right) \psi_n^{(0)} \ \Downarrow \ \sum_m a_{mn}^{(1)} \left( \hat{H}0 - E_n^{(0)} \right) \psi_m^{(0)} = \left( E_n^{(1)} - \hat{H}' \right) \psi_n^{(0)} \ \Downarrow \ \sum_m a {mn}^{(1)} \left( E_m^{(0)} - E_n^{(0)} \right) \psi_m^{(0)} = \left( E_n^{(1)} - \hat{H}' \right) \psi_n^{(0)} \ \Downarrow \ \sum_m a_{mn}^{(1)} \langle \psi_k^{(0)} | E_m^{(0)} - E_n^{(0)} | \psi_m^{(0)} \rangle = \langle \psi_k^{(0)} | E_n^{(1)} - \hat{H}' | \psi_n^{(0)} \rangle \ \Downarrow \ a_{kn}^{(1)} \left( E_k^{(0)} - E_n^{(0)} \right) = E_n^{(1)} \delta_{kn} - \langle \psi_k^{(0)} | \hat{H}' | \psi_n^{(0)} \rangle ( H ^ 0 − E n ( 0 ) ) m ∑ a mn ( 1 ) ψ m ( 0 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ⇓ m ∑ a mn ( 1 ) ( H ^ 0 − E n ( 0 ) ) ψ m ( 0 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ⇓ m ∑ a mn ( 1 ) ( E m ( 0 ) − E n ( 0 ) ) ψ m ( 0 ) = ( E n ( 1 ) − H ^ ′ ) ψ n ( 0 ) ⇓ m ∑ a mn ( 1 ) ⟨ ψ k ( 0 ) ∣ E m ( 0 ) − E n ( 0 ) ∣ ψ m ( 0 ) ⟩ = ⟨ ψ k ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 0 ) ⟩ ⇓ a kn ( 1 ) ( E k ( 0 ) − E n ( 0 ) ) = E n ( 1 ) δ kn − ⟨ ψ k ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩
当 k = n k=n k = n
E n ( 1 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ = H n n ′ E_n^{(1)} = \langle \psi_n^{(0)} | \hat{H}' | \psi_n^{(0)} \rangle = H'_{nn} E n ( 1 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ = H nn ′
当 k ≠ n k \ne n k = n
a k n ( 1 ) = ⟨ ψ k ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ E k ( 0 ) − E m ( 0 ) = H k n ′ E k ( 0 ) − E m ( 0 ) a_{kn}^{(1)} = \frac{\langle \psi_k^{(0)} | \hat{H}' | \psi_n^{(0)} \rangle}{E_k^{(0)}-E_m^{(0)}} = \frac{H'_{kn}}{E_k^{(0)}-E_m^{(0)}} a kn ( 1 ) = E k ( 0 ) − E m ( 0 ) ⟨ ψ k ( 0 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ = E k ( 0 ) − E m ( 0 ) H kn ′
根据 ⟨ ψ n ( 0 ) ∣ ψ n ( 1 ) ⟩ = 0 \langle \psi_n^{(0)} | \psi_n^{(1)} \rangle = 0 ⟨ ψ n ( 0 ) ∣ ψ n ( 1 ) ⟩ = 0 a n n ( 1 ) = 0 a_{nn}^{(1)} = 0 a nn ( 1 ) = 0
ψ n ( 1 ) = ∑ m a m n ( 1 ) ψ m ( 0 ) = ∑ m ≠ n H m n ′ E n ( 0 ) − E m ( 0 ) ψ m ( 0 ) \psi_n^{(1)} = \sum_m a_{mn}^{(1)} \psi_m^{(0)}= \sum_{m \ne n} \frac{H'_{mn}}{E_n^{(0)}-E_m^{(0)}} \psi_m^{(0)} ψ n ( 1 ) = m ∑ a mn ( 1 ) ψ m ( 0 ) = m = n ∑ E n ( 0 ) − E m ( 0 ) H mn ′ ψ m ( 0 )
在二级方程的两侧同乘 ψ n ( 0 ) ∗ \psi_n^{(0)*} ψ n ( 0 ) ∗
⟨ ψ n ( 0 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 1 ) ⟩ + ⟨ ψ n ( 0 ) ∣ E n ( 2 ) ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 0 ) ∣ E n ( 0 ) − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = − ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 1 ) ⟩ + E n ( 2 ) ⇓ E n ( 2 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 1 ) ⟩ \langle \psi_n^{(0)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(2)} \rangle = \langle \psi_n^{(0)} | E_n^{(1)} - \hat{H}' | \psi_n^{(1)} \rangle + \langle \psi_n^{(0)} | E_n^{(2)} | \psi_n^{(0)} \rangle \ \Downarrow \ \langle \psi_n^{(0)} | E_n^{(0)} - E_n^{(0)} | \psi_n^{(2)} \rangle = - \langle \psi_n^{(0)} | \hat{H}' | \psi_n^{(1)} \rangle + E_n^{(2)} \ \Downarrow \ E_n^{(2)} = \langle \psi_n^{(0)} | \hat{H}' | \psi_n^{(1)} \rangle ⟨ ψ n ( 0 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 1 ) ⟩ + ⟨ ψ n ( 0 ) ∣ E n ( 2 ) ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 0 ) ∣ E n ( 0 ) − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = − ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 1 ) ⟩ + E n ( 2 ) ⇓ E n ( 2 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 1 ) ⟩
将 ψ n ( 1 ) \psi_n^{(1)} ψ n ( 1 ) H ′ H' H ′ H m n ′ = ( H n m ′ ) ∗ H'{mn} = (H' {nm})^* H mn ′ = ( H nm ′ ) ∗
E n ( 2 ) = ∑ m ≠ n H m n ′ E n ( 0 ) − E m ( 0 ) ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ m ( 0 ) ⟩ = ∑ m ≠ n H m n ′ H n m ′ E n ( 0 ) − E m ( 0 ) = ∑ m ≠ n ∣ H m n ′ ∣ 2 E n ( 0 ) − E m ( 0 ) E_n^{(2)} = \sum_{m \ne n} \frac{H'{mn}}{E_n^{(0)}-E_m^{(0)}} \langle \psi_n^{(0)} | \hat{H}' | \psi_m^{(0)} \rangle \ \ \ = \sum {m \ne n} \frac{H'{mn}H' {nm}}{E_n^{(0)}-E_m^{(0)}} = \sum_{m \ne n} \frac{|H'_{mn}|^2}{E_n^{(0)}-E_m^{(0)}} E n ( 2 ) = m = n ∑ E n ( 0 ) − E m ( 0 ) H mn ′ ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ m ( 0 ) ⟩ = m = n ∑ E n ( 0 ) − E m ( 0 ) H mn ′ H nm ′ = m = n ∑ E n ( 0 ) − E m ( 0 ) ∣ H mn ′ ∣ 2
在三级方程的两侧同乘 ψ n ( 0 ) ∗ \psi_n^{(0)*} ψ n ( 0 ) ∗
⟨ ψ n ( 0 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 3 ) ⟩ = ⟨ ψ n ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 2 ) ⟩ + ⟨ ψ n ( 0 ) ∣ E n ( 2 ) ∣ ψ n ( 1 ) ⟩ + ⟨ ψ n ( 0 ) ∣ E n ( 3 ) ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 0 ) ∣ E n ( 0 ) − E n ( 0 ) ∣ ψ n ( 3 ) ⟩ = − ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 2 ) ⟩ + E n ( 2 ) ⇓ E n ( 3 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 2 ) ⟩ \langle \psi_n^{(0)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(3)} \rangle = \langle \psi_n^{(0)} | E_n^{(1)} - \hat{H}' | \psi_n^{(2)} \rangle + \langle \psi_n^{(0)} | E_n^{(2)} | \psi_n^{(1)} \rangle + \langle \psi_n^{(0)} | E_n^{(3)} | \psi_n^{(0)} \rangle \ \Downarrow \ \langle \psi_n^{(0)} | E_n^{(0)} - E_n^{(0)} | \psi_n^{(3)} \rangle = - \langle \psi_n^{(0)} | \hat{H}' | \psi_n^{(2)} \rangle + E_n^{(2)} \ \Downarrow \ E_n^{(3)} = \langle \psi_n^{(0)} | \hat{H}' | \psi_n^{(2)} \rangle ⟨ ψ n ( 0 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 3 ) ⟩ = ⟨ ψ n ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 2 ) ⟩ + ⟨ ψ n ( 0 ) ∣ E n ( 2 ) ∣ ψ n ( 1 ) ⟩ + ⟨ ψ n ( 0 ) ∣ E n ( 3 ) ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 0 ) ∣ E n ( 0 ) − E n ( 0 ) ∣ ψ n ( 3 ) ⟩ = − ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 2 ) ⟩ + E n ( 2 ) ⇓ E n ( 3 ) = ⟨ ψ n ( 0 ) ∣ H ^ ′ ∣ ψ n ( 2 ) ⟩
为了不使用 ψ n ( 2 ) \psi_n^{(2)} ψ n ( 2 ) E n ( 3 ) E_n^{(3)} E n ( 3 ) ψ n ( 1 ) ∗ \psi_n^{(1)*} ψ n ( 1 ) ∗
⟨ ψ n ( 1 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 1 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 1 ) ⟩ + ⟨ ψ n ( 1 ) ∣ E n ( 2 ) ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 1 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 1 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 1 ) ⟩ \langle \psi_n^{(1)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(2)} \rangle = \langle \psi_n^{(1)} | E_n^{(1)} - \hat{H}' | \psi_n^{(1)} \rangle + \langle \psi_n^{(1)} | E_n^{(2)} | \psi_n^{(0)} \rangle \ \Downarrow \ \langle \psi_n^{(1)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(2)} \rangle = \langle \psi_n^{(1)} | E_n^{(1)} - \hat{H}' | \psi_n^{(1)} \rangle ⟨ ψ n ( 1 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 1 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 1 ) ⟩ + ⟨ ψ n ( 1 ) ∣ E n ( 2 ) ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 1 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 1 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 1 ) ⟩
在一级方程的两侧同乘 ψ n ( 2 ) ∗ \psi_n^{(2)*} ψ n ( 2 ) ∗
⟨ ψ n ( 2 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = ⟨ ψ n ( 2 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 2 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = − ⟨ ψ n ( 2 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ = − E n ( 3 ) \langle \psi_n^{(2)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(1)} \rangle = \langle \psi_n^{(2)} | E_n^{(1)} - \hat{H}' | \psi_n^{(0)} \rangle \ \Downarrow \ \langle \psi_n^{(2)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(1)} \rangle = - \langle \psi_n^{(2)} | \hat{H}' | \psi_n^{(0)} \rangle = - E_n^{(3)} ⟨ ψ n ( 2 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = ⟨ ψ n ( 2 ) ∣ E n ( 1 ) − H ^ ′ ∣ ψ n ( 0 ) ⟩ ⇓ ⟨ ψ n ( 2 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = − ⟨ ψ n ( 2 ) ∣ H ^ ′ ∣ ψ n ( 0 ) ⟩ = − E n ( 3 )
考虑到 H ^ 0 \hat{H}_0 H ^ 0 ⟨ ψ n ( 1 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 2 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ \langle \psi_n^{(1)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(2)} \rangle = \langle \psi_n^{(2)} | \hat{H}_0 - E_n^{(0)} | \psi_n^{(1)} \rangle ⟨ ψ n ( 1 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 2 ) ⟩ = ⟨ ψ n ( 2 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩
E n ( 3 ) = ⟨ ψ n ( 1 ) ∣ H ^ ′ − E n ( 1 ) ∣ ψ n ( 1 ) ⟩ E_n^{(3)} = \langle \psi_n^{(1)} | \hat{H}' - E_n^{(1)} | \psi_n^{(1)} \rangle E n ( 3 ) = ⟨ ψ n ( 1 ) ∣ H ^ ′ − E n ( 1 ) ∣ ψ n ( 1 ) ⟩
将 ψ n ( 1 ) \psi_n^{(1)} ψ n ( 1 )
E n ( 3 ) = ∑ k ≠ n ( H k n ′ ) ∗ E n ( 0 ) − E k ( 0 ) ∑ m ≠ n H m n ′ E n ( 0 ) − E m ( 0 ) ⟨ ψ k ( 0 ) ∣ H ^ ′ − E n ( 1 ) ∣ ψ m ( 0 ) ⟩ = ∑ k ≠ n ∑ m ≠ n H n k ′ E n ( 0 ) − E k ( 0 ) H m n ′ E n ( 0 ) − E m ( 0 ) ⟨ ψ k ( 0 ) ∣ H ^ ′ ∣ ψ m ( 0 ) ⟩ − E n ( 1 ) ∑ m ≠ n H n m ′ E n ( 0 ) − E m ( 0 ) H m n ′ E n ( 0 ) − E m ( 0 ) = ∑ k ≠ n ∑ m ≠ n H n k ′ H k m ′ H m n ′ ( E n ( 0 ) − E k ( 0 ) ) ( E n ( 0 ) − E m ( 0 ) ) − H n n ′ ∑ m ≠ n ∣ H m n ′ ∣ 2 ( E n ( 0 ) − E m ( 0 ) ) 2 E_n^{(3)} = \sum_{k \ne n} \frac{(H'{kn})^*}{E_n^{(0)}-E_k^{(0)}} \sum {m \ne n} \frac{H'{mn}}{E_n^{(0)}-E_m^{(0)}} \langle \psi_k^{(0)} | \hat{H}' - E_n^{(1)} | \psi_m^{(0)} \rangle \ \ \ = \sum {k \ne n} \sum_{m \ne n} \frac{H'{nk}}{E_n^{(0)}-E_k^{(0)}} \frac{H' {mn}}{E_n^{(0)}-E_m^{(0)}} \langle \psi_k^{(0)} | \hat{H}' | \psi_m^{(0)} \rangle - E_n^{(1)} \sum_{m \ne n} \frac{H'{nm}}{E_n^{(0)}-E_m^{(0)}} \frac{H' {mn}}{E_n^{(0)}-E_m^{(0)}} \ \ \ = \sum_{k \ne n} \sum_{m \ne n} \frac{H'{nk}H' {km}H'{mn}}{(E_n^{(0)}-E_k^{(0)})(E_n^{(0)}-E_m^{(0)})} - H' {nn} \sum_{m \ne n} \frac{|H'_{mn}|^2}{(E_n^{(0)}-E_m^{(0)})^2} E n ( 3 ) = k = n ∑ E n ( 0 ) − E k ( 0 ) ( H kn ′ ) ∗ m = n ∑ E n ( 0 ) − E m ( 0 ) H mn ′ ⟨ ψ k ( 0 ) ∣ H ^ ′ − E n ( 1 ) ∣ ψ m ( 0 ) ⟩ = k = n ∑ m = n ∑ E n ( 0 ) − E k ( 0 ) H nk ′ E n ( 0 ) − E m ( 0 ) H mn ′ ⟨ ψ k ( 0 ) ∣ H ^ ′ ∣ ψ m ( 0 ) ⟩ − E n ( 1 ) m = n ∑ E n ( 0 ) − E m ( 0 ) H nm ′ E n ( 0 ) − E m ( 0 ) H mn ′ = k = n ∑ m = n ∑ ( E n ( 0 ) − E k ( 0 ) ) ( E n ( 0 ) − E m ( 0 ) ) H nk ′ H km ′ H mn ′ − H nn ′ m = n ∑ ( E n ( 0 ) − E m ( 0 ) ) 2 ∣ H mn ′ ∣ 2
若在不考虑微扰时,体系处于简并能级,即 H 0 H_0 H 0 E n ( 0 ) E_n^{(0)} E n ( 0 ) { ϕ n i ( 0 ) } {\phi_{ni}^{(0)}} { ϕ ni ( 0 ) } f n = k f_n = k f n = k n n n H ^ ′ \hat{H}' H ^ ′ { ϕ n i ( 0 ) } {\phi_{ni}^{(0)}} { ϕ ni ( 0 ) }
H j i ′ = ⟨ ϕ n j ( 0 ) ∣ H ^ ′ ∣ ϕ n i ( 0 ) ⟩ H'{ji} = \langle \phi {nj}^{(0)} | \hat{H}' | \phi_{ni}^{(0)} \rangle H ji ′ = ⟨ ϕ nj ( 0 ) ∣ H ^ ′ ∣ ϕ ni ( 0 ) ⟩
求解久期方程
det ( H j i ′ − E n ( 1 ) δ j i ) = 0 \det\left( H'{ji} - E_n^{(1)} \delta {ji} \right) = 0 det ( H ji ′ − E n ( 1 ) δ ji ) = 0
可以得到该能级的 k k k 一阶微扰能 E n ( 1 ) E_{n}^{(1)} E n ( 1 )
∑ i = 1 k a i ( 0 ) ( H j i ′ − E n ( 1 ) δ j i ) = 0 \sum_{i=1}^k a_i^{(0)} \left( H'{ji} - E_n^{(1)} \delta {ji} \right) = 0 i = 1 ∑ k a i ( 0 ) ( H ji ′ − E n ( 1 ) δ ji ) = 0
可以得到对应的 k k k { a i ( 0 ) } { a_i^{(0)} } { a i ( 0 ) } k k k 零级波函数
ψ n ( 0 ) = ∑ i = 1 k a i ( 0 ) ϕ n i ( 0 ) \psi_n^{(0)} = \sum_{i=1}^k a_i^{(0)} \phi_{ni}^{(0)} ψ n ( 0 ) = i = 1 ∑ k a i ( 0 ) ϕ ni ( 0 )
如果解得的 E n ( 1 ) E_n^{(1)} E n ( 1 )
已知
H ^ 0 ϕ n i ( 0 ) = E n ϕ n i ( 0 ) ( i = 1 , 2 , ⋯ , k ) \hat{H}0 \phi {ni}^{(0)} = E_n \phi_{ni}^{(0)} \kern 2em (i=1,2,\cdots,k) H ^ 0 ϕ ni ( 0 ) = E n ϕ ni ( 0 ) ( i = 1 , 2 , ⋯ , k )
在引入微扰后,新的零级波函数尚不能确定,可设为
ψ n ( 0 ) = ∑ i = 1 k a i ( 0 ) ϕ n i ( 0 ) \psi_n^{(0)} = \sum_{i=1}^k a_i^{(0)} \phi_{ni}^{(0)} ψ n ( 0 ) = i = 1 ∑ k a i ( 0 ) ϕ ni ( 0 )
代入一级方程,结合 { ϕ n i ( 0 ) } {\phi_{ni}^{(0)}} { ϕ ni ( 0 ) }
( H ^ 0 − E n ( 0 ) ) ψ n ( 1 ) = ( E n ( 1 ) − H ^ ′ ) ∑ i = 1 k a i ( 0 ) ϕ n i ( 0 ) ⇓ ( H ^ 0 − E n ( 0 ) ) ψ n ( 1 ) = ∑ i = 1 k a i ( 0 ) ( E n ( 1 ) − H ^ ′ ) ϕ n i ( 0 ) ⇓ ⟨ ϕ n j ( 0 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = ∑ i = 1 k a i ( 0 ) ⟨ ϕ n j ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ϕ n i ( 0 ) ⟩ ⇓ ⟨ ϕ n j ( 0 ) ∣ E n ( 0 ) − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = ∑ i = 1 k a i ( 0 ) ( E n ( 1 ) δ j i − ⟨ ϕ n j ( 0 ) ∣ H ^ ′ ∣ ϕ n i ( 0 ) ⟩ ) ⇓ ∑ i = 1 k a i ( 0 ) ( ⟨ ϕ n j ( 0 ) ∣ H ^ ′ ∣ ϕ n i ( 0 ) ⟩ − E n ( 1 ) δ j i ) = 0 \left( \hat{H}0 - E_n^{(0)} \right) \psi_n^{(1)} = \left( E_n^{(1)} - \hat{H}' \right) \sum {i=1}^k a_i^{(0)} \phi_{ni}^{(0)} \ \Downarrow \ \left( \hat{H}0 - E_n^{(0)} \right) \psi_n^{(1)} = \sum {i=1}^k a_i^{(0)} \left( E_n^{(1)} - \hat{H}' \right) \phi_{ni}^{(0)} \ \Downarrow \ \langle \phi_{nj}^{(0)} | \hat{H}0 - E_n^{(0)} | \psi_n^{(1)} \rangle = \sum {i=1}^k a_i^{(0)} \langle \phi_{nj}^{(0)} | E_n^{(1)} - \hat{H}' | \phi_{ni}^{(0)} \rangle \ \Downarrow \ \langle \phi_{nj}^{(0)} | E_n^{(0)} - E_n^{(0)} | \psi_n^{(1)} \rangle = \sum_{i=1}^k a_i^{(0)} \left( E_n^{(1)} \delta_{ji} - \langle \phi_{nj}^{(0)} | \hat{H}' | \phi_{ni}^{(0)} \rangle \right) \ \Downarrow \ \sum_{i=1}^k a_i^{(0)} \left( \langle \phi_{nj}^{(0)} | \hat{H}' | \phi_{ni}^{(0)} \rangle - E_n^{(1)} \delta_{ji} \right) = 0 ( H ^ 0 − E n ( 0 ) ) ψ n ( 1 ) = ( E n ( 1 ) − H ^ ′ ) i = 1 ∑ k a i ( 0 ) ϕ ni ( 0 ) ⇓ ( H ^ 0 − E n ( 0 ) ) ψ n ( 1 ) = i = 1 ∑ k a i ( 0 ) ( E n ( 1 ) − H ^ ′ ) ϕ ni ( 0 ) ⇓ ⟨ ϕ nj ( 0 ) ∣ H ^ 0 − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = i = 1 ∑ k a i ( 0 ) ⟨ ϕ nj ( 0 ) ∣ E n ( 1 ) − H ^ ′ ∣ ϕ ni ( 0 ) ⟩ ⇓ ⟨ ϕ nj ( 0 ) ∣ E n ( 0 ) − E n ( 0 ) ∣ ψ n ( 1 ) ⟩ = i = 1 ∑ k a i ( 0 ) ( E n ( 1 ) δ ji − ⟨ ϕ nj ( 0 ) ∣ H ^ ′ ∣ ϕ ni ( 0 ) ⟩ ) ⇓ i = 1 ∑ k a i ( 0 ) ( ⟨ ϕ nj ( 0 ) ∣ H ^ ′ ∣ ϕ ni ( 0 ) ⟩ − E n ( 1 ) δ ji ) = 0
记 H j i ′ = ⟨ ϕ n j ( 0 ) ∣ H ^ ′ ∣ ϕ n i ( 0 ) ⟩ H'{ji} = \langle \phi {nj}^{(0)} | \hat{H}' | \phi_{ni}^{(0)} \rangle H ji ′ = ⟨ ϕ nj ( 0 ) ∣ H ^ ′ ∣ ϕ ni ( 0 ) ⟩
det ( H j i ′ − E n ( 1 ) δ j i ) = 0 \det\left( H'{ji} - E_n^{(1)} \delta {ji} \right) = 0 det ( H ji ′ − E n ( 1 ) δ ji ) = 0
此部分内容不作为考试要求
如果Hamilton量不含时,即 ∂ H ^ ∂ t = 0 \frac{\partial \hat{H}}{\partial t} = 0 ∂ t ∂ H ^ = 0 ∣ ψ ( 0 ) ⟩ | \psi(0) \rangle ∣ ψ ( 0 )⟩
∣ ψ ( t ) ⟩ = U ^ ( t ) ∣ ψ ( 0 ) ⟩ = e − i ℏ H ^ t ∣ ψ ( 0 ) ⟩ | \psi(t) \rangle = \hat{U}(t) | \psi(0) \rangle = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} | \psi(0) \rangle ∣ ψ ( t )⟩ = U ^ ( t ) ∣ ψ ( 0 )⟩ = e − ℏ i H ^ t ∣ ψ ( 0 )⟩
将初态按能量本征态展开,即
∣ ψ ( 0 ) ⟩ = ∑ n a n ∣ ψ n ⟩ | \psi(0) \rangle = \sum_n a_n | \psi_n \rangle ∣ ψ ( 0 )⟩ = n ∑ a n ∣ ψ n ⟩
其中
H ^ ∣ ψ n ⟩ = E n ∣ ψ n ⟩ a n = ⟨ ψ n ∣ ψ ( 0 ) ⟩ ( 不显含时间 ) \hat{H} | \psi_n \rangle = E_n | \psi_n \rangle \ \ \ a_n = \langle \psi_n | \psi(0) \rangle \kern 1em (不显含时间) H ^ ∣ ψ n ⟩ = E n ∣ ψ n ⟩ a n = ⟨ ψ n ∣ ψ ( 0 )⟩ ( 不显含时间 )
则 t t t
∣ ψ ( t ) ⟩ = e − i ℏ H ^ t ∑ n a n ∣ ψ n ⟩ = ∑ n a n e − i ℏ E n t ∣ ψ n ⟩ | \psi(t) \rangle = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} \sum_n a_n | \psi_n \rangle = \sum_n a_n \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle ∣ ψ ( t )⟩ = e − ℏ i H ^ t n ∑ a n ∣ ψ n ⟩ = n ∑ a n e − ℏ i E n t ∣ ψ n ⟩
如果初态为能量本征态,即
∣ ψ ( 0 ) ⟩ = ∣ ψ k ⟩ | \psi(0) \rangle = | \psi_k \rangle ∣ ψ ( 0 )⟩ = ∣ ψ k ⟩
则 t t t
∣ ψ ( t ) ⟩ = e − i ℏ E k t ∣ ψ k ⟩ | \psi(t) \rangle = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_kt} | \psi_k \rangle ∣ ψ ( t )⟩ = e − ℏ i E k t ∣ ψ k ⟩
这种量子态,称为定态 ;若初态不是能量本征态,则称为非定态 。
对于含时Hamilton量 H ^ ( t ) \hat{H}(t) H ^ ( t )
H ^ ( t ) = H ^ 0 + H ^ ′ ( t ) \hat{H}(t) = \hat{H}_0 + \hat{H}'(t) H ^ ( t ) = H ^ 0 + H ^ ′ ( t )
若体系初态为 H ^ 0 \hat{H}_0 H ^ 0 ∣ ψ k ⟩ | \psi_k \rangle ∣ ψ k ⟩
∣ ψ ( t ) ⟩ = ∑ n C n k ( t ) e − i ℏ E n t ∣ ψ n ⟩ | \psi(t) \rangle = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle ∣ ψ ( t )⟩ = n ∑ C nk ( t ) e − ℏ i E n t ∣ ψ n ⟩
再次测量时,有一定的概率离开初态而处于其它定态,这种现象叫做量子跃迁 。
在一级近似下,从 ψ k \psi_k ψ k ψ k ′ \psi_{k'} ψ k ′ 跃迁振幅 为
C k ′ k ( t ) = δ k ′ k + 1 i ℏ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ C_{k'k}(t) = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'k}\tau} \mathrm{d}\tau C k ′ k ( t ) = δ k ′ k + i ℏ 1 ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ
其中
H k ′ k ′ ( t ) = ⟨ k ′ ∣ H ^ ′ ( t ) ∣ k ⟩ ω k ′ k = E k ′ − E k ℏ H'{k'k}(t) = \langle k' | \hat{H}'(t) | k \rangle \ \ \ \omega {k'k} = \frac{E_{k'}-E_k}{\hbar} H k ′ k ′ ( t ) = ⟨ k ′ ∣ H ^ ′ ( t ) ∣ k ⟩ ω k ′ k = ℏ E k ′ − E k
对于 k ′ ≠ k k' \ne k k ′ = k
C k ′ k ( t ) = 1 i ℏ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ C_{k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'k}\tau} \mathrm{d}\tau C k ′ k ( t ) = i ℏ 1 ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ
跃迁概率 为
P k ′ k ( t ) = ∣ C k ′ k ( t ) ∣ 2 = 1 ℏ 2 ∣ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ ∣ 2 P_{k'k}(t) = |C_{k'k}(t)|^2 = \frac{1}{\hbar^2} \left| \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'k}\tau} \mathrm{d}\tau \right|^2 P k ′ k ( t ) = ∣ C k ′ k ( t ) ∣ 2 = ℏ 2 1 ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ 2
单位时间内的跃迁概率,即跃迁速率 为
w k ′ k ( t ) = d d t ∣ C k ′ k ( t ) ∣ 2 = 1 ℏ 2 d d t ∣ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ ∣ 2 w_{k'k}(t) = \frac{\mathrm{d}}{\mathrm{d}t} |C_{k'k}(t)|^2 = \frac{1}{\hbar^2} \frac{\mathrm{d}}{\mathrm{d}t} \left| \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'k}\tau} \mathrm{d}\tau \right|^2 w k ′ k ( t ) = d t d ∣ C k ′ k ( t ) ∣ 2 = ℏ 2 1 d t d ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ 2
{ ∣ ψ ( t ) ⟩ = ∑ n C n k ( t ) e − i ℏ E n t ∣ ψ n ⟩ C n k ( 0 ) = δ n k \begin{cases} | \psi(t) \rangle = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle \ C_{nk}(0) = \delta_{nk} \end{cases} { ∣ ψ ( t )⟩ = ∑ n C nk ( t ) e − ℏ i E n t ∣ ψ n ⟩ C nk ( 0 ) = δ nk
将 t t t
i ℏ ∂ ∂ t ∑ n C n k ( t ) e − i ℏ E n t ∣ ψ n ⟩ = ( H ^ 0 + H ^ ′ ( t ) ) ∑ n C n k ( t ) e − i ℏ E n t ∣ ψ n ⟩ ⇓ i ℏ ∑ n [ ∂ ∂ t C n k ( t ) ] e − i ℏ E n t ∣ n ⟩ + i ℏ ∑ n C n k ( t ) [ ∂ ∂ t e − i ℏ E n t ] ∣ n ⟩ = ∑ n C n k ( t ) e − i ℏ E n t H ^ 0 ∣ n ⟩ + ∑ n C n k ( t ) e − i ℏ E n t H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ ∑ n C ˙ n k ( t ) e − i ℏ E n t ∣ n ⟩ + ∑ n C n k ( t ) e − i ℏ E n t E n ∣ n ⟩ = ∑ n C n k ( t ) e − i ℏ E n t E n ∣ n ⟩ + ∑ n C n k ( t ) e − i ℏ E n t H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ ∑ n C ˙ n k ( t ) e − i ℏ E n t ∣ n ⟩ = ∑ n C n k ( t ) e − i ℏ E n t H ^ ′ ( t ) ∣ n ⟩ \mathrm{i}\hbar \frac{\partial}{\partial t} \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle = \left( \hat{H}0 + \hat{H}'(t) \right) \sum_n C {nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle \ \Downarrow \ \mathrm{i}\hbar \sum_n \left[ \frac{\partial}{\partial t} C_{nk}(t) \right] \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | n \rangle + \mathrm{i}\hbar \sum_n C_{nk}(t) \left[ \frac{\partial}{\partial t} \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \right] | n \rangle \ \ \ = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}0 | n \rangle + \sum_n C {nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \sum_n \dot{C}{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | n \rangle + \sum_n C {nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} E_n | n \rangle \ \ \ = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} E_n | n \rangle + \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \sum_n \dot{C}{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | n \rangle = \sum_n C {nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}'(t) | n \rangle i ℏ ∂ t ∂ n ∑ C nk ( t ) e − ℏ i E n t ∣ ψ n ⟩ = ( H ^ 0 + H ^ ′ ( t ) ) n ∑ C nk ( t ) e − ℏ i E n t ∣ ψ n ⟩ ⇓ i ℏ n ∑ [ ∂ t ∂ C nk ( t ) ] e − ℏ i E n t ∣ n ⟩ + i ℏ n ∑ C nk ( t ) [ ∂ t ∂ e − ℏ i E n t ] ∣ n ⟩ = n ∑ C nk ( t ) e − ℏ i E n t H ^ 0 ∣ n ⟩ + n ∑ C nk ( t ) e − ℏ i E n t H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ n ∑ C ˙ nk ( t ) e − ℏ i E n t ∣ n ⟩ + n ∑ C nk ( t ) e − ℏ i E n t E n ∣ n ⟩ = n ∑ C nk ( t ) e − ℏ i E n t E n ∣ n ⟩ + n ∑ C nk ( t ) e − ℏ i E n t H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ n ∑ C ˙ nk ( t ) e − ℏ i E n t ∣ n ⟩ = n ∑ C nk ( t ) e − ℏ i E n t H ^ ′ ( t ) ∣ n ⟩
对上式左乘 ⟨ k ′ ∣ \langle k' | ⟨ k ′ ∣
i ℏ ∑ n C ˙ n k ( t ) e − i ℏ E n t ⟨ k ′ ∣ n ⟩ = ∑ n C n k ( t ) e − i ℏ E n t ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ C ˙ k ′ k ( t ) e − i ℏ E k ′ t = ∑ n C n k ( t ) e − i ℏ E n t ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ C ˙ k ′ k ( t ) = ∑ n C n k ( t ) e i ℏ ( E k ′ − E n ) t ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩ \mathrm{i}\hbar \sum_n \dot{C}{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \langle k' | n \rangle = \sum_n C {nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \langle k' | \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \dot{C}{k'k}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E {k'}t} = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \langle k' | \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \dot{C}{k'k}(t) = \sum_n C {nk}(t) \mathrm{e}^{\frac{\mathrm{i}}{\hbar}(E_{k'}-E_n)t} \langle k' | \hat{H}'(t) | n \rangle i ℏ n ∑ C ˙ nk ( t ) e − ℏ i E n t ⟨ k ′ ∣ n ⟩ = n ∑ C nk ( t ) e − ℏ i E n t ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ C ˙ k ′ k ( t ) e − ℏ i E k ′ t = n ∑ C nk ( t ) e − ℏ i E n t ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩ ⇓ i ℏ C ˙ k ′ k ( t ) = n ∑ C nk ( t ) e ℏ i ( E k ′ − E n ) t ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩
记
H k ′ n ′ ( t ) = ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩ ω k ′ n = E k ′ − E n ℏ H'{k'n}(t) = \langle k' | \hat{H}'(t) | n \rangle \ \ \ \omega {k'n} = \frac{E_{k'}-E_n}{\hbar} H k ′ n ′ ( t ) = ⟨ k ′ ∣ H ^ ′ ( t ) ∣ n ⟩ ω k ′ n = ℏ E k ′ − E n
则跃迁振幅满足方程
{ i ℏ C ˙ k ′ k ( t ) = ∑ n H k ′ n ′ ( t ) e i ω k ′ n t C n k ( t ) C k ′ k ( 0 ) = δ k ′ k \begin{cases} \mathrm{i}\hbar \dot{C}{k'k}(t) = \sum_n H' {k'n}(t) \mathrm{e}^{\mathrm{i}\omega_{k'n}t} C_{nk}(t) \ C_{k'k}(0) = \delta_{k'k} \end{cases} { i ℏ C ˙ k ′ k ( t ) = ∑ n H k ′ n ′ ( t ) e i ω k ′ n t C nk ( t ) C k ′ k ( 0 ) = δ k ′ k
方程两边对 t t t
C k ′ k ( t ) = C k ′ k ( 0 ) + 1 i ℏ ∫ 0 t ∑ n H k ′ n ′ ( τ ) e i ω k ′ n τ C n k ( τ ) d τ = δ k ′ k + 1 i ℏ ∫ 0 t ∑ n H k ′ n ′ ( τ ) e i ω k ′ n τ C n k ( τ ) d τ C_{k'k}(t) = C_{k'k}(0) + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'n}\tau} C_{nk}(\tau) \mathrm{d}\tau \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'n}\tau} C_{nk}(\tau) \mathrm{d}\tau C k ′ k ( t ) = C k ′ k ( 0 ) + i ℏ 1 ∫ 0 t n ∑ H k ′ n ′ ( τ ) e i ω k ′ n τ C nk ( τ ) d τ = δ k ′ k + i ℏ 1 ∫ 0 t n ∑ H k ′ n ′ ( τ ) e i ω k ′ n τ C nk ( τ ) d τ
该积分方程可迭代求解,即
C k ′ k ( t ) = δ k ′ k + 1 i ℏ ∫ 0 t ∑ n H k ′ n ′ ( τ ) e i ω k ′ n τ [ δ n k + 1 i ℏ ∫ 0 t ∑ m H n m ′ ( τ ′ ) e i ω n m τ ′ C m k ( τ ′ ) d τ ′ ] d τ = δ k ′ k + 1 i ℏ ∫ 0 t ∑ n H k ′ n ′ ( τ ) e i ω k ′ n τ δ n k d τ + 1 i ℏ ∫ 0 t ∑ n H k ′ n ′ ( τ ) e i ω k ′ n τ [ 1 i ℏ ∫ 0 t ∑ m H n m ′ ( τ ′ ) e i ω n m τ ′ C m k ( τ ′ ) d τ ′ ] d τ = δ k ′ k + 1 i ℏ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ + 1 i ℏ ∫ 0 t ∑ n H k ′ n ′ ( τ ) e i ω k ′ n τ [ 1 i ℏ ∫ 0 t ∑ m H n m ′ ( τ ′ ) e i ω n m τ ′ C m k ( τ ′ ) d τ ′ ] d τ C_{k'k}(t) \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'n}\tau} \left[ \delta_{nk} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_m H'{nm}(\tau') \mathrm{e}^{\mathrm{i}\omega {nm}\tau'} C_{mk}(\tau') \mathrm{d}\tau' \right] \mathrm{d}\tau \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'n}\tau} \delta_{nk}\mathrm{d}\tau \ \ \ + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'n}\tau} \left[ \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_m H'{nm}(\tau') \mathrm{e}^{\mathrm{i}\omega {nm}\tau'} C_{mk}(\tau') \mathrm{d}\tau' \right] \mathrm{d}\tau \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'k}\tau} \mathrm{d}\tau \ \ \ + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'n}\tau} \left[ \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_m H'{nm}(\tau') \mathrm{e}^{\mathrm{i}\omega {nm}\tau'} C_{mk}(\tau') \mathrm{d}\tau' \right] \mathrm{d}\tau C k ′ k ( t ) = δ k ′ k + i ℏ 1 ∫ 0 t n ∑ H k ′ n ′ ( τ ) e i ω k ′ n τ [ δ nk + i ℏ 1 ∫ 0 t m ∑ H nm ′ ( τ ′ ) e i ω nm τ ′ C mk ( τ ′ ) d τ ′ ] d τ = δ k ′ k + i ℏ 1 ∫ 0 t n ∑ H k ′ n ′ ( τ ) e i ω k ′ n τ δ nk d τ + i ℏ 1 ∫ 0 t n ∑ H k ′ n ′ ( τ ) e i ω k ′ n τ [ i ℏ 1 ∫ 0 t m ∑ H nm ′ ( τ ′ ) e i ω nm τ ′ C mk ( τ ′ ) d τ ′ ] d τ = δ k ′ k + i ℏ 1 ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ + i ℏ 1 ∫ 0 t n ∑ H k ′ n ′ ( τ ) e i ω k ′ n τ [ i ℏ 1 ∫ 0 t m ∑ H nm ′ ( τ ′ ) e i ω nm τ ′ C mk ( τ ′ ) d τ ′ ] d τ
故零级近似
C k ′ k ( 0 ) ( t ) = δ k ′ k C^{(0)}{k'k}(t) = \delta {k'k} C k ′ k ( 0 ) ( t ) = δ k ′ k
一级近似
C k ′ k ( 1 ) ( t ) = 1 i ℏ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ C^{(1)}{k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H' {k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau C k ′ k ( 1 ) ( t ) = i ℏ 1 ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ
对初态按各简并的各本征态展开,按照各本征态出现的概率对各本征态向末态的跃迁概率求加权平均和 。
对向末态的各简并态的跃迁概率求和 。
考虑周期微扰
H ^ ′ ( t ) = H ′ e − i ω t \hat{H}'(t) = H' \mathrm{e}^{-\mathrm{i}\omega t} H ^ ′ ( t ) = H ′ e − i ω t
则在 t t t ∣ k ⟩ | k \rangle ∣ k ⟩ ∣ k ′ ⟩ ( k ′ ≠ k ) | k' \rangle \ (k' \ne k) ∣ k ′ ⟩ ( k ′ = k ) 跃迁振幅 为
C k ′ k ( t ) = 1 i ℏ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ = 1 i ℏ ∫ 0 t ⟨ k ′ ∣ H ′ ∣ k ⟩ e i ( ω k ′ k − ω ) τ d τ = 1 i ℏ ⟨ k ′ ∣ H ′ ∣ k ⟩ e i ( ω k ′ k − ω ) t − 1 i ( ω k ′ k − ω ) C_{k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'k}\tau} \mathrm{d}\tau \ \ \ = \frac{1}{\mathrm{i}\hbar} \int_0^t \langle k' | H' | k \rangle \mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)\tau} \mathrm{d}\tau \ \ \ = \frac{1}{\mathrm{i}\hbar} \langle k' | H' | k \rangle \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\mathrm{i}(\omega_{k'k}-\omega)} C k ′ k ( t ) = i ℏ 1 ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ = i ℏ 1 ∫ 0 t ⟨ k ′ ∣ H ′ ∣ k ⟩ e i ( ω k ′ k − ω ) τ d τ = i ℏ 1 ⟨ k ′ ∣ H ′ ∣ k ⟩ i ( ω k ′ k − ω ) e i ( ω k ′ k − ω ) t − 1
记 H k ′ k ′ = ⟨ k ′ ∣ H ′ ∣ k ⟩ H'_{k'k} = \langle k' | H' | k \rangle H k ′ k ′ = ⟨ k ′ ∣ H ′ ∣ k ⟩ 跃迁概率
P k ′ k ( t ) = ∣ C k ′ k ( t ) ∣ 2 = 4 ∣ H k ′ k ′ ∣ 2 ℏ 2 { sin [ ω k ′ k − ω ) t / 2 ] ω k ′ k − ω } 2 P_{k'k}(t) = |C_{k'k}(t)|^2 = \frac{4|H'{k'k}|^2}{\hbar^2} \left{ \frac{\sin[\omega {k'k}-\omega)t/2]}{\omega_{k'k}-\omega} \right}^2 P k ′ k ( t ) = ∣ C k ′ k ( t ) ∣ 2 = ℏ 2 4∣ H k ′ k ′ ∣ 2 { ω k ′ k − ω sin [ ω k ′ k − ω ) t /2 ] } 2
利用 lim α → ∞ sin 2 α x x 2 = π α δ ( x ) \lim_{\alpha\to\infty} \frac{\sin^2\alpha x}{x^2} = \pi\alpha\delta(x) lim α → ∞ x 2 s i n 2 αx = π α δ ( x ) ( ω k ′ k − ω ) t ≫ 1 (\omega_{k'k} - \omega)t \gg 1 ( ω k ′ k − ω ) t ≫ 1
P k ′ k ( t ) = 2 π t ℏ 2 ∣ H k ′ k ′ ∣ 2 δ ( ω k ′ k − ω ) P_{k'k}(t) = \frac{2\pi t}{\hbar^2} |H'{k'k}|^2 \delta(\omega {k'k}-\omega) P k ′ k ( t ) = ℏ 2 2 π t ∣ H k ′ k ′ ∣ 2 δ ( ω k ′ k − ω )
跃迁速率 为
w k ′ k = ∂ ∂ t P k ′ k ( t ) = 2 π ℏ 2 ∣ H k ′ k ′ ∣ 2 δ ( ω k ′ k − ω ) = 2 π ℏ ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k − ℏ ω ) w_{k'k} = \frac{\partial}{\partial t} P_{k'k}(t) = \frac{2\pi}{\hbar^2} |H'{k'k}|^2 \delta(\omega {k'k}-\omega) \ \ \ = \frac{2\pi}{\hbar} |H'{k'k}|^2 \delta(E {k'}-E_k-\hbar\omega) w k ′ k = ∂ t ∂ P k ′ k ( t ) = ℏ 2 2 π ∣ H k ′ k ′ ∣ 2 δ ( ω k ′ k − ω ) = ℏ 2 π ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k − ℏ ω )
由此可见,如果周期微扰持续的时间足够长,即远大于体系的内禀特征时间,则跃迁速率将与时间无关。
上述结果适用于分立谱的情况,对于连续谱,有意义的是计算跃迁到能量 E k ′ E_{k'} E k ′ ρ ( E k ′ ) \rho(E_{k'}) ρ ( E k ′ ) 总跃迁概率
P total ( t ) = ∫ P k ′ k ( t ) ρ ( E k ′ ) d E k ′ = ∫ 2 π t ℏ ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k − ℏ ω ) ρ ( E k ′ ) d E k ′ = 2 π t ℏ ∣ H k ′ k ′ ∣ 2 ρ ( E k + ℏ ω ) P_{\text{total}}(t) = \int P_{k'k}(t) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \int \frac{2\pi t}{\hbar} |H'{k'k}|^2 \delta(E {k'}-E_k-\hbar\omega) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \frac{2\pi t}{\hbar} |H'{k'k}|^2 \rho(E {k} + \hbar\omega) P total ( t ) = ∫ P k ′ k ( t ) ρ ( E k ′ ) d E k ′ = ∫ ℏ 2 π t ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k − ℏ ω ) ρ ( E k ′ ) d E k ′ = ℏ 2 π t ∣ H k ′ k ′ ∣ 2 ρ ( E k + ℏ ω )
总跃迁速率
w total = ∂ ∂ t P total ( t ) = 2 π ℏ ∣ H k ′ k ′ ∣ 2 ρ ( E k + ℏ ω ) w_{\text{total}} = \frac{\partial}{\partial t} P_{\text{total}}(t) = \frac{2\pi}{\hbar} |H'{k'k}|^2 \rho(E {k} + \hbar\omega) w total = ∂ t ∂ P total ( t ) = ℏ 2 π ∣ H k ′ k ′ ∣ 2 ρ ( E k + ℏ ω )
只在一段时间间隔(如 0 ∼ T 0 \sim T 0 ∼ T 常微扰 ,即
H ^ ′ ( t ) = H ′ [ θ ( t ) − θ ( t − T ) ] \hat{H}'(t) = H' [\theta(t) - \theta(t-T)] H ^ ′ ( t ) = H ′ [ θ ( t ) − θ ( t − T )]
其中 θ ( t ) \theta(t) θ ( t )
θ ( t ) = { 0 , t < 0 1 , t > 0 \theta(t) = \begin{cases} 0 , & t<0 \ 1 , & t>0 \end{cases} θ ( t ) = { 0 , 1 , t < 0 t > 0
故
H ^ ′ ( t ) = { H ′ , 0 ≤ t < T 0 , t > T \hat{H}'(t) = \begin{cases} H' , & 0 \le t < T \ 0 , & t > T \end{cases} H ^ ′ ( t ) = { H ′ , 0 , 0 ≤ t < T t > T
则一级近似下的跃迁振幅 为
C k ′ k ( 1 ) ( t ) = 1 i ℏ ∫ − ∞ t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ = − H k ′ k ′ ( t ) e i ω k ′ k t ℏ ω k ′ k + ∫ − ∞ t ∂ H k ′ k ′ ( τ ) ∂ τ e i ω k ′ k τ ℏ ω k ′ k d τ = − H k ′ k ′ ( t ) e i ω k ′ k t ℏ ω k ′ k + ∫ − ∞ t H k ′ k ′ [ δ ( τ ) − δ ( τ − T ) ] e i ω k ′ k τ ℏ ω k ′ k d τ C^{(1)}{k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int {-\infty}^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega {k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{H'{k'k}(t)\mathrm{e}^{\mathrm{i}\omega {k'k}t}}{\hbar\omega_{k'k}} + \int_{-\infty}^t \frac{\partial H'{k'k}(\tau)}{\partial \tau} \frac{\mathrm{e}^{\mathrm{i}\omega {k'k}\tau}}{\hbar\omega_{k'k}} \mathrm{d}\tau \ \ \ = -\frac{H'{k'k}(t)\mathrm{e}^{\mathrm{i}\omega {k'k}t}}{\hbar\omega_{k'k}} + \int_{-\infty}^t H'{k'k} [\delta(\tau) - \delta(\tau-T)] \frac{\mathrm{e}^{\mathrm{i}\omega {k'k}\tau}}{\hbar\omega_{k'k}} \mathrm{d}\tau C k ′ k ( 1 ) ( t ) = i ℏ 1 ∫ − ∞ t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ = − ℏ ω k ′ k H k ′ k ′ ( t ) e i ω k ′ k t + ∫ − ∞ t ∂ τ ∂ H k ′ k ′ ( τ ) ℏ ω k ′ k e i ω k ′ k τ d τ = − ℏ ω k ′ k H k ′ k ′ ( t ) e i ω k ′ k t + ∫ − ∞ t H k ′ k ′ [ δ ( τ ) − δ ( τ − T )] ℏ ω k ′ k e i ω k ′ k τ d τ
当 t > T t>T t > T
C k ′ k ( 1 ) ( t ) = H k ′ k ′ ℏ ω k ′ k ( 1 − e i ω k ′ k T ) C^{(1)}{k'k}(t) = \frac{H' {k'k}}{\hbar\omega_{k'k}} \left( 1 - \mathrm{e}^{\mathrm{i}\omega_{k'k}T} \right) C k ′ k ( 1 ) ( t ) = ℏ ω k ′ k H k ′ k ′ ( 1 − e i ω k ′ k T )
故 k ′ ≠ k k' \ne k k ′ = k 跃迁概率 为
P k ′ k ( t ) = ∣ C k ′ k ( t ) ∣ 2 = ∣ H k ′ k ′ ∣ 2 ℏ 2 sin 2 ( ω k ′ k T / 2 ) ( ω k ′ k / 2 ) 2 P_{k'k}(t) = |C_{k'k}(t)|^2 = \frac{|H'{k'k}|^2}{\hbar^2} \frac{\sin^2(\omega {k'k}T/2)}{(\omega_{k'k}/2)^2} P k ′ k ( t ) = ∣ C k ′ k ( t ) ∣ 2 = ℏ 2 ∣ H k ′ k ′ ∣ 2 ( ω k ′ k /2 ) 2 sin 2 ( ω k ′ k T /2 )
利用 lim α → ∞ sin 2 α x x 2 = π α δ ( x ) \lim_{\alpha\to\infty} \frac{\sin^2\alpha x}{x^2} = \pi\alpha\delta(x) lim α → ∞ x 2 s i n 2 αx = π α δ ( x ) ω k ′ k T ≫ 1 \omega_{k'k}T \gg 1 ω k ′ k T ≫ 1
P k ′ k ( t ) = 2 π T ℏ 2 ∣ H k ′ k ′ ∣ 2 δ ( ω k ′ k ) = 2 π T ℏ ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k ) P_{k'k}(t) = \frac{2\pi T}{\hbar^2} |H'{k'k}|^2 \delta(\omega {k'k}) = \frac{2\pi T}{\hbar} |H'{k'k}|^2 \delta(E {k'} - E_k) P k ′ k ( t ) = ℏ 2 2 π T ∣ H k ′ k ′ ∣ 2 δ ( ω k ′ k ) = ℏ 2 π T ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k )
跃迁速率 为
w k ′ k = P k ′ k ( t ) T = 2 π ℏ ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k ) w_{k'k} = \frac{P_{k'k}(t)}{T} = \frac{2\pi}{\hbar} |H'{k'k}|^2 \delta(E {k'}-E_k) w k ′ k = T P k ′ k ( t ) = ℏ 2 π ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k )
由此可见,如果常微扰作用的时间足够长,即远大于体系的内禀特征时间,则跃迁速率将与时间无关。
上述结果适用于分立谱的情况,对于连续谱,有意义的是计算跃迁到能量 E k ′ E_{k'} E k ′ ρ ( E k ′ ) \rho(E_{k'}) ρ ( E k ′ ) 总跃迁概率
P total ( t ) = ∫ P k ′ k ( t ) ρ ( E k ′ ) d E k ′ = ∫ 2 π T ℏ ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k ) ρ ( E k ′ ) d E k ′ = 2 π T ℏ ∣ H k ′ k ′ ∣ 2 ρ ( E k ) P_{\text{total}}(t) = \int P_{k'k}(t) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \int \frac{2\pi T}{\hbar} |H'{k'k}|^2 \delta(E {k'}-E_k) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \frac{2\pi T}{\hbar} |H'{k'k}|^2 \rho(E {k}) P total ( t ) = ∫ P k ′ k ( t ) ρ ( E k ′ ) d E k ′ = ∫ ℏ 2 π T ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k ) ρ ( E k ′ ) d E k ′ = ℏ 2 π T ∣ H k ′ k ′ ∣ 2 ρ ( E k )
总跃迁速率 (Fermi黄金规则)
w total = ∫ w k ′ k ρ ( E k ′ ) d E k ′ = ∫ 2 π ℏ ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k ) ρ ( E k ′ ) d E k ′ = 2 π ℏ ∣ H k ′ k ′ ∣ 2 ρ ( E k ) w_{\text{total}} = \int w_{k'k} \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \int \frac{2\pi}{\hbar} |H'{k'k}|^2 \delta(E {k'}-E_k) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \frac{2\pi}{\hbar} |H'{k'k}|^2 \rho(E {k}) w total = ∫ w k ′ k ρ ( E k ′ ) d E k ′ = ∫ ℏ 2 π ∣ H k ′ k ′ ∣ 2 δ ( E k ′ − E k ) ρ ( E k ′ ) d E k ′ = ℏ 2 π ∣ H k ′ k ′ ∣ 2 ρ ( E k )
在光的照射下,原子可能吸收光而从低能级跃迁到较高能级,称为光的吸收 (obsorption);或从较高能级跃迁到较低能级并放出光,称为受激辐射 (induced radiation);如果原子本来处于激发能级,即使没有外界光的照射,也可能跃迁到某些较低能级而放出光来,称为自发辐射 (spontaneous radiation)。
注:本节均使用高斯单位制CGS。
先假设入射光为平面单色光,其电磁场强度分别为
E ⃗ = E ⃗ 0 cos ( ω t − k ⃗ ⋅ r ⃗ ) B ⃗ = k ⃗ × E ⃗ ∣ k ⃗ ∣ \vec{E} = \vec{E}_0 \cos(\omega t - \vec{k} \cdot \vec{r}) \ \ \ \vec{B} = \vec{k} \times \frac{\vec{E}}{|\vec{k}|} E = E 0 cos ( ω t − k ⋅ r ) B = k × ∣ k ∣ E
由于在原子中,电子的速度 v ≪ c v \ll c v ≪ c ∣ e c v ⃗ × B ⃗ ∣ \left| \frac{e}{c} \vec{v} \times \vec{B} \right| c e v × B ∣ e E ⃗ ∣ \left| e \vec{E} \right| e E λ \lambda λ a a a k ⃗ ⋅ r ⃗ ∼ 2 π a / λ ≪ 1 \vec{k} \cdot \vec{r} \sim 2\pi a / \lambda \ll 1 k ⋅ r ∼ 2 πa / λ ≪ 1
E ⃗ = E ⃗ 0 cos ( ω t ) \vec{E} = \vec{E}_0 \cos(\omega t) E = E 0 cos ( ω t )
入射可见光对于原子中电子的作用可表示为
H ^ ′ ( t ) = − D ⃗ ⋅ E ⃗ = − D ⃗ ⋅ E ⃗ 0 cos ( ω t ) = W cos ( ω t ) \hat{H}'(t) = - \vec{D} \cdot \vec{E} = - \vec{D} \cdot \vec{E}_0 \cos(\omega t) = W \cos(\omega t) H ^ ′ ( t ) = − D ⋅ E = − D ⋅ E 0 cos ( ω t ) = W cos ( ω t )
其中
W = − D ⃗ ⋅ E ⃗ 0 , D ⃗ = − e r ⃗ ( 电偶极矩 ) W = - \vec{D} \cdot \vec{E}_0 , \kern 2em \vec{D} = -e \vec{r} (电偶极矩) W = − D ⋅ E 0 , D = − e r ( 电偶极矩 )
电偶极矩与电场作用引起的跃迁称为电偶极跃迁 。
在一级近似下,对于从 E k → E k ′ ( E k ′ > E k ) E_k \to E_{k'} \kern 1em (E_{k'}>E_k) E k → E k ′ ( E k ′ > E k ) 跃迁振幅
C k ′ k ( 1 ) ( t ) = − W k ′ k 2 ℏ e i ( ω k ′ k − ω ) t − 1 ω k ′ k − ω C^{(1)}{k'k}(t) = -\frac{W {k'k}}{2\hbar} \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\omega_{k'k}-\omega} C k ′ k ( 1 ) ( t ) = − 2ℏ W k ′ k ω k ′ k − ω e i ( ω k ′ k − ω ) t − 1
跃迁概率
P k ′ k ( t ) = ∣ C k ′ k ( 1 ) ( t ) ∣ 2 = ∣ W k ′ k ∣ 2 4 ℏ 2 sin 2 [ ( ω k ′ k − ω ) t / 2 ] [ ( ω k ′ k − ω ) / 2 ] 2 P_{k'k}(t) = \left| C^{(1)}{k'k}(t) \right|^2 = \frac{|W {k'k}|^2}{4\hbar^2} \frac{\sin^2[(\omega_{k'k}-\omega)t/2]}{[(\omega_{k'k}-\omega)/2]^2} P k ′ k ( t ) = C k ′ k ( 1 ) ( t ) 2 = 4 ℏ 2 ∣ W k ′ k ∣ 2 [( ω k ′ k − ω ) /2 ] 2 sin 2 [( ω k ′ k − ω ) t /2 ]
当时间足够长时,只有 ω ≈ ω k ′ k \omega \approx \omega_{k'k} ω ≈ ω k ′ k
P k ′ k ( t ) = π t 4 ℏ 2 ∣ W k ′ k ∣ 2 δ [ ( ω k ′ k − ω ) / 2 ] P_{k'k}(t) = \frac{\pi t}{4\hbar^2} |W_{k'k}|^2\ \delta[(\omega_{k'k}-\omega)/2] P k ′ k ( t ) = 4 ℏ 2 π t ∣ W k ′ k ∣ 2 δ [( ω k ′ k − ω ) /2 ]
跃迁速率
w k ′ k = d d t P k ′ k = π 2 ℏ 2 ∣ W k ′ k ∣ 2 δ ( ω k ′ k − ω ) = π 2 ℏ 2 ∣ D ⃗ k ′ k ⋅ E ⃗ 0 ∣ 2 δ ( ω k ′ k − ω ) = π 2 ℏ 2 ∣ D ⃗ k ′ k ∣ 2 E 0 2 cos 2 θ δ ( ω k ′ k − ω ) w_{k'k} = \frac{\mathrm{d}}{\mathrm{d}t} P_{k'k} = \frac{\pi}{2\hbar^2} |W_{k'k}|^2\ \delta(\omega_{k'k}-\omega) \ \ \ = \frac{\pi}{2\hbar^2} |\vec{D}{k'k} \cdot \vec{E}0|^2\ \delta(\omega {k'k}-\omega) \ \ \ = \frac{\pi}{2\hbar^2} |\vec{D} {k'k}|^2 E_0^2\ \cos^2\theta\ \delta(\omega_{k'k}-\omega) w k ′ k = d t d P k ′ k = 2 ℏ 2 π ∣ W k ′ k ∣ 2 δ ( ω k ′ k − ω ) = 2 ℏ 2 π ∣ D k ′ k ⋅ E 0 ∣ 2 δ ( ω k ′ k − ω ) = 2 ℏ 2 π ∣ D k ′ k ∣ 2 E 0 2 cos 2 θ δ ( ω k ′ k − ω )
其中 θ \theta θ D ⃗ k ′ k \vec{D}_{k'k} D k ′ k E 0 E_0 E 0 E ⃗ 0 \vec{E}_0 E 0 cos 2 θ \cos^2\theta cos 2 θ
cos 2 θ ‾ = 1 4 π ∫ d Ω cos 2 θ = 1 4 π ∫ 0 2 π d φ ∫ 0 π sin θ cos 2 θ d θ = 1 3 \overline{\cos^2\theta} = \frac{1}{4\pi} \int \mathrm{d}\Omega\ \cos^2\theta \ \ \ = \frac{1}{4\pi} \int_{0}^{2\pi} \mathrm{d}\varphi \int_{0}^{\pi} \sin\theta \cos^2\theta \mathrm{d}\theta = \frac13 cos 2 θ = 4 π 1 ∫ d Ω cos 2 θ = 4 π 1 ∫ 0 2 π d φ ∫ 0 π sin θ cos 2 θ d θ = 3 1
故非偏振光的跃迁速率
w k ′ k = π 6 ℏ 2 ∣ D ⃗ k ′ k ∣ 2 E 0 2 δ ( ω k ′ k − ω ) w_{k'k} = \frac{\pi}{6\hbar^2} |\vec{D}{k'k}|^2 E_0^2\ \delta(\omega {k'k}-\omega) w k ′ k = 6 ℏ 2 π ∣ D k ′ k ∣ 2 E 0 2 δ ( ω k ′ k − ω )
对于非单色光,用 ρ ( ω ) \rho(\omega) ρ ( ω ) ω \omega ω
ρ ( ω ) = 1 8 π ( E 2 + B 2 ) ‾ = 1 4 π E 2 ‾ = E 0 2 ( ω ) 4 π 1 T ∫ 0 T cos 2 ω t d t = 1 8 π E 0 2 ( ω ) ⇓ E 0 2 ( ω ) = 8 π ρ ( ω ) \rho(\omega) = \frac{1}{8\pi} \overline{(E^2+B^2)} \ \ \ = \frac{1}{4\pi} \overline{E^2} \ \ \ = \frac{E_0^2(\omega)}{4\pi} \frac{1}{T} \int_0^T \cos^2 \omega t\ \mathrm{d}t \ \ \ = \frac{1}{8\pi} E_0^2(\omega) \ \Downarrow \ E_0^2(\omega) = 8\pi\rho(\omega) ρ ( ω ) = 8 π 1 ( E 2 + B 2 ) = 4 π 1 E 2 = 4 π E 0 2 ( ω ) T 1 ∫ 0 T cos 2 ω t d t = 8 π 1 E 0 2 ( ω ) ⇓ E 0 2 ( ω ) = 8 π ρ ( ω )
故非单色光的跃迁速率
w total = ∫ − ∞ + ∞ w k ′ k d ω = ∫ − ∞ + ∞ π 6 ℏ 2 ∣ D ⃗ k ′ k ∣ 2 E 0 2 ( ω ) δ ( ω k ′ k − ω ) d ω = 4 π 2 3 ℏ 2 ∣ D ⃗ k ′ k ∣ 2 ∫ − ∞ + ∞ ρ ( ω ) δ ( ω k ′ k − ω ) d ω = 4 π 2 3 ℏ 2 ∣ D ⃗ k ′ k ∣ 2 ρ ( ω k ′ k ) = 4 π 2 e 2 3 ℏ 2 ∣ r ⃗ k ′ k ∣ 2 ρ ( ω k ′ k ) w_{\text{total}} = \int_{-\infty}^{+\infty} w_{k'k}\ \mathrm{d}\omega \ \ \ = \int_{-\infty}^{+\infty} \frac{\pi}{6\hbar^2} |\vec{D}{k'k}|^2 E_0^2(\omega)\ \delta(\omega {k'k}-\omega) \mathrm{d}\omega \ \ \ = \frac{4\pi^2}{3\hbar^2} |\vec{D}{k'k}|^2 \int {-\infty}^{+\infty} \rho(\omega) \delta(\omega_{k'k}-\omega) \mathrm{d}\omega \ \ \ = \frac{4\pi^2}{3\hbar^2} |\vec{D}{k'k}|^2 \rho(\omega {k'k}) \ \ \ = \frac{4\pi^2e^2}{3\hbar^2} |\vec{r}{k'k}|^2 \rho(\omega {k'k}) w total = ∫ − ∞ + ∞ w k ′ k d ω = ∫ − ∞ + ∞ 6 ℏ 2 π ∣ D k ′ k ∣ 2 E 0 2 ( ω ) δ ( ω k ′ k − ω ) d ω = 3 ℏ 2 4 π 2 ∣ D k ′ k ∣ 2 ∫ − ∞ + ∞ ρ ( ω ) δ ( ω k ′ k − ω ) d ω = 3 ℏ 2 4 π 2 ∣ D k ′ k ∣ 2 ρ ( ω k ′ k ) = 3 ℏ 2 4 π 2 e 2 ∣ r k ′ k ∣ 2 ρ ( ω k ′ k )
其中 ∣ r ⃗ k ′ k ∣ 2 = ∣ x k ′ k ∣ 2 + ∣ y k ′ k ∣ 2 + ∣ z k ′ k ∣ 2 |\vec{r}{k'k}|^2 = |x {k'k}|^2 + |y_{k'k}|^2 + |z_{k'k}|^2 ∣ r k ′ k ∣ 2 = ∣ x k ′ k ∣ 2 + ∣ y k ′ k ∣ 2 + ∣ z k ′ k ∣ 2
跃迁的快慢与入射光中频率为 ω k ′ k \omega_{k'k} ω k ′ k ρ ( ω k ′ k ) \rho(\omega_{k'k}) ρ ( ω k ′ k ) ω k ′ k \omega_{k'k} ω k ′ k E k ↔ E k ′ E_{k} \leftrightarrow E_{k'} E k ↔ E k ′
把 H ^ ′ ( t ) = − W cos ( ω t ) \hat{H}'(t)= - W \cos(\omega t) H ^ ′ ( t ) = − W cos ( ω t )
C k ′ k ( 1 ) ( t ) = 1 i ℏ ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ = − W k ′ k i ℏ ∫ 0 t cos ( ω τ ) e i ω k ′ k τ d τ = − W k ′ k 2 i ℏ ∫ 0 t ( e i ω τ + e − i ω τ ) e i ω k ′ k τ d τ = − W k ′ k 2 ℏ [ e i ( ω k ′ k + ω ) t − 1 ω k ′ k + ω + e i ( ω k ′ k − ω ) t − 1 ω k ′ k − ω ] C^{(1)}{k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H' {k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{W_{k'k}}{\mathrm{i}\hbar} \int_0^t \cos(\omega\tau) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{W_{k'k}}{2\mathrm{i}\hbar} \int_0^t (\mathrm{e}^{\mathrm{i}\omega\tau} + \mathrm{e}^{-\mathrm{i}\omega\tau}) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{W_{k'k}}{2\hbar} \left[ \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}+\omega)t}-1}{\omega_{k'k}+\omega} + \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\omega_{k'k}-\omega} \right] C k ′ k ( 1 ) ( t ) = i ℏ 1 ∫ 0 t H k ′ k ′ ( τ ) e i ω k ′ k τ d τ = − i ℏ W k ′ k ∫ 0 t cos ( ω τ ) e i ω k ′ k τ d τ = − 2 i ℏ W k ′ k ∫ 0 t ( e i ω τ + e − i ω τ ) e i ω k ′ k τ d τ = − 2ℏ W k ′ k [ ω k ′ k + ω e i ( ω k ′ k + ω ) t − 1 + ω k ′ k − ω e i ( ω k ′ k − ω ) t − 1 ]
对于可见光以及紫外光, ω \omega ω ω ≈ ω k ′ k \omega \approx \omega_{k'k} ω ≈ ω k ′ k
C k ′ k ( 1 ) ( t ) = − W k ′ k 2 ℏ e i ( ω k ′ k − ω ) t − 1 ω k ′ k − ω C^{(1)}{k'k}(t) = -\frac{W {k'k}}{2\hbar} \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\omega_{k'k}-\omega} C k ′ k ( 1 ) ( t ) = − 2ℏ W k ′ k ω k ′ k − ω e i ( ω k ′ k − ω ) t − 1
电偶极跃迁的角动量选择定则 为:初末态量子数满足
Δ l = ± 1 , Δ m l = 0 , ± 1 , Δ m s = 0 \Delta l = \pm1 ,\kern 1em \Delta m_l = 0, \pm 1 , \kern 1em \Delta m_s = 0 Δ l = ± 1 , Δ m l = 0 , ± 1 , Δ m s = 0
其中对于电场平行于 z z z Δ m l = 0 \Delta m_l = 0 Δ m l = 0 x x x y y y Δ m l = ± 1 \Delta m_l = \pm1 Δ m l = ± 1
原子的宇称 π = ( − 1 ) l \pi = (-1)^l π = ( − 1 ) l
如果使用耦合表象,则选择定则表述为
Δ l = ± 1 , Δ j = 0 , ± 1 , Δ m j = 0 , ± 1 \Delta l = \pm1 ,\kern 1em \Delta j = 0, \pm 1 , \kern 1em \Delta m_j = 0, \pm1 Δ l = ± 1 , Δ j = 0 , ± 1 , Δ m j = 0 , ± 1
考虑矩阵元 r ⃗ k ′ k \vec{r}_{k'k} r k ′ k
⟨ k ′ ∣ r ⃗ ∣ k ⟩ = ⟨ n ′ l ′ m l ′ s ′ m s ′ ∣ r ⃗ ∣ n l m l s m s ⟩ = ⟨ n ′ l ′ m l ′ ∣ r ⃗ ∣ n l m l ⟩ ⟨ 1 2 m s ′ ∣ 1 2 m s ⟩ = ⟨ n ′ l ′ m l ′ ∣ r ⃗ ∣ n l m l ⟩ δ m s ′ m s \langle k' | \vec{r} | k \rangle = \langle n'l'm_l's'm_s' | \vec{r} | nlm_lsm_s \rangle \ \ \ = \langle n'l'm_l' | \vec{r} | nlm_l \rangle \langle \frac12m_s' | \frac12m_s \rangle \ \ \ = \langle n'l'm_l' | \vec{r} | nlm_l \rangle \delta_{m_s'm_s} ⟨ k ′ ∣ r ∣ k ⟩ = ⟨ n ′ l ′ m l ′ s ′ m s ′ ∣ r ∣ n l m l s m s ⟩ = ⟨ n ′ l ′ m l ′ ∣ r ∣ n l m l ⟩ ⟨ 2 1 m s ′ ∣ 2 1 m s ⟩ = ⟨ n ′ l ′ m l ′ ∣ r ∣ n l m l ⟩ δ m s ′ m s
故只有 m s ′ = m s m_s' = m_s m s ′ = m s
对于电场平行于 z z z z k ′ k z_{k'k} z k ′ k
z k ′ k = ⟨ n ′ l ′ m l ′ ∣ r cos θ ∣ n l m l ⟩ = ⟨ R n ′ l ′ ( r ) Y l ′ m l ′ ( θ , φ ) ∣ r cos θ ∣ R n l ( r ) Y l m l ( θ , φ ) ⟩ = ( R n ′ l ′ , r R n l ) ( Y l ′ m l ′ , cos θ Y l m l ) z_{k'k} = \langle n'l'm_l' | r\cos\theta | nlm_l \rangle \ \ \ = \langle R_{n'l'}(r) \mathrm{Y}{l'm_l'}(\theta,\varphi) | r\cos\theta | R {nl}(r) \mathrm{Y}{lm_l}(\theta,\varphi) \rangle \ \ \ = (R {n'l'} , r R_{nl}) (\mathrm{Y}{l'm_l'} , \cos\theta \mathrm{Y} {lm_l}) z k ′ k = ⟨ n ′ l ′ m l ′ ∣ r cos θ ∣ n l m l ⟩ = ⟨ R n ′ l ′ ( r ) Y l ′ m l ′ ( θ , φ ) ∣ r cos θ ∣ R n l ( r ) Y l m l ( θ , φ )⟩ = ( R n ′ l ′ , r R n l ) ( Y l ′ m l ′ , cos θ Y l m l )
其中 ( R n ′ l ′ , r R n l ) ≠ 0 (R_{n'l'} , r R_{nl}) \ne 0 ( R n ′ l ′ , r R n l ) = 0
cos θ Y l , m l = ( l + 1 ) 2 − m l 2 ( 2 l + 1 ) ( 2 l + 3 ) Y l + 1 , m l + l 2 − m l 2 ( 2 l − 1 ) ( 2 l + 1 ) Y l − 1 , m l \cos\theta\mathrm{Y}{l,m_l} = \sqrt{\frac{(l+1)^2-m_l^2}{(2l+1)(2l+3)}} \mathrm{Y} {l+1,m_l} + \sqrt{\frac{l^2-m_l^2}{(2l-1)(2l+1)}} \mathrm{Y}_{l-1,m_l} cos θ Y l , m l = ( 2 l + 1 ) ( 2 l + 3 ) ( l + 1 ) 2 − m l 2 Y l + 1 , m l + ( 2 l − 1 ) ( 2 l + 1 ) l 2 − m l 2 Y l − 1 , m l
可得
( Y l ′ m l ′ , cos θ Y l m l ) = ( l + 1 ) 2 − m l 2 ( 2 l + 1 ) ( 2 l + 3 ) δ l ′ , l + 1 δ m l ′ , m l + l 2 − m l 2 ( 2 l − 1 ) ( 2 l + 1 ) δ l ′ , l − 1 δ m l ′ , m l (\mathrm{Y}{l'm_l'} , \cos\theta \mathrm{Y} {lm_l}) \ \ \ = \sqrt{\frac{(l+1)^2-m_l^2}{(2l+1)(2l+3)}} \delta_{l',l+1}\delta_{m_l',m_l} + \sqrt{\frac{l^2-m_l^2}{(2l-1)(2l+1)}} \delta_{l',l-1}\delta_{m_l',m_l} ( Y l ′ m l ′ , cos θ Y l m l ) = ( 2 l + 1 ) ( 2 l + 3 ) ( l + 1 ) 2 − m l 2 δ l ′ , l + 1 δ m l ′ , m l + ( 2 l − 1 ) ( 2 l + 1 ) l 2 − m l 2 δ l ′ , l − 1 δ m l ′ , m l
故当 Δ l = ± 1 , Δ m l = 0 \Delta l = \pm1 ,\kern 1em \Delta m_l = 0 Δ l = ± 1 , Δ m l = 0
对于电场平行于 x x x x k ′ k x_{k'k} x k ′ k
x k ′ k = ⟨ n ′ l ′ m l ′ ∣ r sin θ cos φ ∣ n l m l ⟩ = ⟨ R n ′ l ′ ( r ) Y l ′ m l ′ ( θ , φ ) ∣ r 2 sin θ ( e i φ + e − i φ ) ∣ R n l ( r ) Y l m l ( θ , φ ) ⟩ = 1 2 ( R n ′ l ′ , r R n l ) ( Y l ′ m l ′ , sin θ ( e i φ + e − i φ ) Y l m l ) x_{k'k} = \langle n'l'm_l' | r\sin\theta\cos\varphi | nlm_l \rangle \ \ \ = \langle R_{n'l'}(r) \mathrm{Y}{l'm_l'}(\theta,\varphi) | \frac{r}{2}\sin\theta(\mathrm{e}^{\mathrm{i}\varphi}+\mathrm{e}^{-\mathrm{i}\varphi}) | R {nl}(r) \mathrm{Y}{lm_l}(\theta,\varphi) \rangle \ \ \ = \frac12 (R {n'l'} , r R_{nl}) (\mathrm{Y}{l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}+\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y} {lm_l}) x k ′ k = ⟨ n ′ l ′ m l ′ ∣ r sin θ cos φ ∣ n l m l ⟩ = ⟨ R n ′ l ′ ( r ) Y l ′ m l ′ ( θ , φ ) ∣ 2 r sin θ ( e i φ + e − i φ ) ∣ R n l ( r ) Y l m l ( θ , φ )⟩ = 2 1 ( R n ′ l ′ , r R n l ) ( Y l ′ m l ′ , sin θ ( e i φ + e − i φ ) Y l m l )
其中 ( R n ′ l ′ , r R n l ) ≠ 0 (R_{n'l'} , r R_{nl}) \ne 0 ( R n ′ l ′ , r R n l ) = 0
e ± i φ sin θ Y l , m l = ± ( l ± m l + 1 ) ( l ± m l + 2 ) ( 2 l + 1 ) ( 2 l + 3 ) Y l + 1 , m l ± 1 ∓ ( l ∓ m l ) ( l ∓ m l − 1 ) ( 2 l − 1 ) ( 2 l + 1 ) Y l − 1 , m l ± 1 \mathrm{e}^{\pm\mathrm{i}\varphi}\sin\theta\mathrm{Y}{l,m_l} = \pm \sqrt{\frac{(l\pm m_l+1)(l\pm m_l+2)}{(2l+1)(2l+3)}} \mathrm{Y} {l+1,m_l\pm1} \mp \sqrt{\frac{(l\mp m_l)(l\mp m_l-1)}{(2l-1)(2l+1)}} \mathrm{Y}_{l-1,m_l\pm1} e ± i φ sin θ Y l , m l = ± ( 2 l + 1 ) ( 2 l + 3 ) ( l ± m l + 1 ) ( l ± m l + 2 ) Y l + 1 , m l ± 1 ∓ ( 2 l − 1 ) ( 2 l + 1 ) ( l ∓ m l ) ( l ∓ m l − 1 ) Y l − 1 , m l ± 1
可得
( Y l ′ m l ′ , sin θ ( e i φ + e − i φ ) Y l m l ) = ( l + m l + 1 ) ( l + m l + 2 ) ( 2 l + 1 ) ( 2 l + 3 ) δ l + 1 , m l + 1 − ( l − m l ) ( l − m l − 1 ) ( 2 l − 1 ) ( 2 l + 1 ) δ l − 1 , m l + 1 − ( l − m l + 1 ) ( l − m l + 2 ) ( 2 l + 1 ) ( 2 l + 3 ) δ l + 1 , m l − 1 + ( l − m l ) ( l − m l − 1 ) ( 2 l − 1 ) ( 2 l + 1 ) δ l − 1 , m l − 1 (\mathrm{Y}{l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}+\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y} {lm_l}) \ \ \ = \sqrt{\frac{(l+m_l+1)(l+m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l+1} - \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l+1} \ \ \ - \sqrt{\frac{(l-m_l+1)(l-m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l-1} + \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l-1} ( Y l ′ m l ′ , sin θ ( e i φ + e − i φ ) Y l m l ) = ( 2 l + 1 ) ( 2 l + 3 ) ( l + m l + 1 ) ( l + m l + 2 ) δ l + 1 , m l + 1 − ( 2 l − 1 ) ( 2 l + 1 ) ( l − m l ) ( l − m l − 1 ) δ l − 1 , m l + 1 − ( 2 l + 1 ) ( 2 l + 3 ) ( l − m l + 1 ) ( l − m l + 2 ) δ l + 1 , m l − 1 + ( 2 l − 1 ) ( 2 l + 1 ) ( l − m l ) ( l − m l − 1 ) δ l − 1 , m l − 1
故当 Δ l = ± 1 , Δ m l = ± 1 \Delta l = \pm1 ,\kern 1em \Delta m_l = \pm 1 Δ l = ± 1 , Δ m l = ± 1
对于电场平行于 y y y y k ′ k y_{k'k} y k ′ k
y k ′ k = ⟨ n ′ l ′ m l ′ ∣ r sin θ sin φ ∣ n l m l ⟩ = ⟨ R n ′ l ′ ( r ) Y l ′ m l ′ ( θ , φ ) ∣ r 2 i sin θ ( e i φ − e − i φ ) ∣ R n l ( r ) Y l m l ( θ , φ ) ⟩ = 1 2 i ( R n ′ l ′ , r R n l ) ( Y l ′ m l ′ , sin θ ( e i φ − e − i φ ) Y l m l ) y_{k'k} = \langle n'l'm_l' | r\sin\theta\sin\varphi | nlm_l \rangle \ \ \ = \langle R_{n'l'}(r) \mathrm{Y}{l'm_l'}(\theta,\varphi) | \frac{r}{2\mathrm{i}}\sin\theta(\mathrm{e}^{\mathrm{i}\varphi}-\mathrm{e}^{-\mathrm{i}\varphi}) | R {nl}(r) \mathrm{Y}{lm_l}(\theta,\varphi) \rangle \ \ \ = \frac{1}{2\mathrm{i}} (R {n'l'} , r R_{nl}) (\mathrm{Y}{l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}-\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y} {lm_l}) y k ′ k = ⟨ n ′ l ′ m l ′ ∣ r sin θ sin φ ∣ n l m l ⟩ = ⟨ R n ′ l ′ ( r ) Y l ′ m l ′ ( θ , φ ) ∣ 2 i r sin θ ( e i φ − e − i φ ) ∣ R n l ( r ) Y l m l ( θ , φ )⟩ = 2 i 1 ( R n ′ l ′ , r R n l ) ( Y l ′ m l ′ , sin θ ( e i φ − e − i φ ) Y l m l )
其中 ( R n ′ l ′ , r R n l ) ≠ 0 (R_{n'l'} , r R_{nl}) \ne 0 ( R n ′ l ′ , r R n l ) = 0
e ± i φ sin θ Y l , m l = ± ( l ± m l + 1 ) ( l ± m l + 2 ) ( 2 l + 1 ) ( 2 l + 3 ) Y l + 1 , m l ± 1 ∓ ( l ∓ m l ) ( l ∓ m l − 1 ) ( 2 l − 1 ) ( 2 l + 1 ) Y l − 1 , m l ± 1 \mathrm{e}^{\pm\mathrm{i}\varphi}\sin\theta\mathrm{Y}{l,m_l} = \pm \sqrt{\frac{(l\pm m_l+1)(l\pm m_l+2)}{(2l+1)(2l+3)}} \mathrm{Y} {l+1,m_l\pm1} \mp \sqrt{\frac{(l\mp m_l)(l\mp m_l-1)}{(2l-1)(2l+1)}} \mathrm{Y}_{l-1,m_l\pm1} e ± i φ sin θ Y l , m l = ± ( 2 l + 1 ) ( 2 l + 3 ) ( l ± m l + 1 ) ( l ± m l + 2 ) Y l + 1 , m l ± 1 ∓ ( 2 l − 1 ) ( 2 l + 1 ) ( l ∓ m l ) ( l ∓ m l − 1 ) Y l − 1 , m l ± 1
可得
( Y l ′ m l ′ , sin θ ( e i φ − e − i φ ) Y l m l ) = ( l + m l + 1 ) ( l + m l + 2 ) ( 2 l + 1 ) ( 2 l + 3 ) δ l + 1 , m l + 1 − ( l − m l ) ( l − m l − 1 ) ( 2 l − 1 ) ( 2 l + 1 ) δ l − 1 , m l + 1 + ( l − m l + 1 ) ( l − m l + 2 ) ( 2 l + 1 ) ( 2 l + 3 ) δ l + 1 , m l − 1 − ( l − m l ) ( l − m l − 1 ) ( 2 l − 1 ) ( 2 l + 1 ) δ l − 1 , m l − 1 (\mathrm{Y}{l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}-\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y} {lm_l}) \ \ \ = \sqrt{\frac{(l+m_l+1)(l+m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l+1} - \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l+1} \ \ \ + \sqrt{\frac{(l-m_l+1)(l-m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l-1} - \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l-1} ( Y l ′ m l ′ , sin θ ( e i φ − e − i φ ) Y l m l ) = ( 2 l + 1 ) ( 2 l + 3 ) ( l + m l + 1 ) ( l + m l + 2 ) δ l + 1 , m l + 1 − ( 2 l − 1 ) ( 2 l + 1 ) ( l − m l ) ( l − m l − 1 ) δ l − 1 , m l + 1 + ( 2 l + 1 ) ( 2 l + 3 ) ( l − m l + 1 ) ( l − m l + 2 ) δ l + 1 , m l − 1 − ( 2 l − 1 ) ( 2 l + 1 ) ( l − m l ) ( l − m l − 1 ) δ l − 1 , m l − 1
故当 Δ l = ± 1 , Δ m l = ± 1 \Delta l = \pm1 ,\kern 1em \Delta m_l = \pm 1 Δ l = ± 1 , Δ m l = ± 1
在强度为 ρ ( ω ) \rho(\omega) ρ ( ω ) k k k k ′ k' k ′ E k ′ > E k E_{k'}>E_k E k ′ > E k
w k ′ k = B k ′ k ρ ( ω k ′ k ) w_{k'k} = B_{k'k} \rho(\omega_{k'k}) w k ′ k = B k ′ k ρ ( ω k ′ k )
其中吸收系数
B k ′ k = 4 π 2 e 2 3 ℏ 2 ∣ r ⃗ k ′ k ∣ 2 B_{k'k} = \frac{4\pi^2e^2}{3\hbar^2} |\vec{r}_{k'k}|^2 B k ′ k = 3 ℏ 2 4 π 2 e 2 ∣ r k ′ k ∣ 2
从 k ′ k' k ′ k k k
w k k ′ = B k k ′ ρ ( ω k ′ k ) w_{kk'} = B_{kk'} \rho(\omega_{k'k}) w k k ′ = B k k ′ ρ ( ω k ′ k )
其中受激辐射系数
B k k ′ = 4 π 2 e 2 3 ℏ 2 ∣ r ⃗ k k ′ ∣ 2 B_{kk'} = \frac{4\pi^2e^2}{3\hbar^2} |\vec{r}_{kk'}|^2 B k k ′ = 3 ℏ 2 4 π 2 e 2 ∣ r k k ′ ∣ 2
由于 r ⃗ ^ \hat{\vec{r}} r ^ r ⃗ k ′ k = r ⃗ k k ′ ∗ \vec{r}{k'k} = \vec{r}^* {kk'} r k ′ k = r k k ′ ∗
B k ′ k = B k k ′ B_{k'k} = B_{kk'} B k ′ k = B k k ′
即受激辐射系数等于吸收系数,他们都与入射光强度无关,只决定于原子的自身性质。
根据Boltzmann分布律,处于平衡状态时,粒子数 n n n E k ′ ≠ E k E_{k'} \ne E_k E k ′ = E k n k ′ ≠ n k n_{k'} \ne n_k n k ′ = n k n k ′ < n k n_{k'} < n_k n k ′ < n k
n k B k ′ k ρ ( ω k ′ k ) > n k ′ B k k ′ ρ ( ω k ′ k ) n_k\ B_{k'k}\ \rho(\omega_{k'k}) > n_{k'}\ B_{kk'}\ \rho(\omega_{k'k}) n k B k ′ k ρ ( ω k ′ k ) > n k ′ B k k ′ ρ ( ω k ′ k )
故如只有受激辐射,就无法与吸收过程达到平衡,出自热力学平衡的要求,必须引进自发辐射 ,在等式右侧加上一项,即
n k B k ′ k ρ ( ω k ′ k ) = n k ′ [ B k k ′ ρ ( ω k ′ k ) + A k k ′ ] n_k\ B_{k'k}\ \rho(\omega_{k'k}) = n_{k'}\ [ B_{kk'}\ \rho(\omega_{k'k}) + A_{kk'} ] n k B k ′ k ρ ( ω k ′ k ) = n k ′ [ B k k ′ ρ ( ω k ′ k ) + A k k ′ ]
其中 A k k ′ A_{kk'} A k k ′ 自发辐射系数 ,表示在没有外界光照射的条件下,单位时间内原子从 k ′ k' k ′ k k k
结合 n k / n k ′ = e ℏ ω k ′ k / k T n_k / n_{k'} = \mathrm{e}^{\hbar\omega_{k'k}/kT} n k / n k ′ = e ℏ ω k ′ k / k T
ρ ( ω k ′ k ) = A k k ′ B k k ′ 1 n k / n k ′ − 1 = A k k ′ B k k ′ 1 e ℏ ω k ′ k / k T − 1 ⟶ T → + ∞ A k k ′ B k k ′ k T ℏ ω k ′ k \rho(\omega_{k'k}) = \frac{A_{kk'}}{B_{kk'}} \frac{1}{n_k / n_{k'} - 1} = \frac{A_{kk'}}{B_{kk'}} \frac{1}{\mathrm{e}^{\hbar\omega_{k'k}/kT} - 1} \ \ \ \overset{T\to+\infty}{\longrightarrow} \frac{A_{kk'}}{B_{kk'}} \frac{kT}{\hbar\omega_{k'k}} ρ ( ω k ′ k ) = B k k ′ A k k ′ n k / n k ′ − 1 1 = B k k ′ A k k ′ e ℏ ω k ′ k / k T − 1 1 ⟶ T → + ∞ B k k ′ A k k ′ ℏ ω k ′ k k T
结合Planck黑体辐射公式
ρ ( ω ) = ℏ ω 3 π 2 c 3 1 e ℏ ω k ′ k / k T − 1 \rho(\omega) = \frac{\hbar\omega^3}{\pi^2c^3} \frac{1}{\mathrm{e}^{\hbar\omega_{k'k}/kT} - 1} ρ ( ω ) = π 2 c 3 ℏ ω 3 e ℏ ω k ′ k / k T − 1 1
可得自发辐射系数的表达式为
A k k ′ = ℏ ω k ′ k 3 π 2 c 3 B k ′ k = 4 e 2 ω k ′ k 3 3 ℏ c 3 ∣ r ⃗ k ′ k ∣ 2 A_{kk'} = \frac{\hbar\omega_{k'k}^3}{\pi^2c^3} B_{k'k} = \frac{4e^2\omega_{k'k}^3}{3\hbar c^3} |\vec{r}_{k'k}|^2 A k k ′ = π 2 c 3 ℏ ω k ′ k 3 B k ′ k = 3ℏ c 3 4 e 2 ω k ′ k 3 ∣ r k ′ k ∣ 2
自发辐射的选择定则与吸收和受激辐射的相同。
散射是具有确定动量 的入射粒子与靶粒子发生相互作用后,入射粒子、靶粒子或产生的碎片沿不同角度出射的过程。
设一束粒子以稳定的入射流密度 j i j_i j i d n \mathrm{d}n d n ( θ , φ ) (\theta,\varphi) ( θ , φ ) d Ω \mathrm{d}\Omega d Ω 散射截面
σ ( θ , φ ) = 1 j i ( d n d Ω ) \sigma(\theta,\varphi) = \frac{1}{j_i} \left( \frac{\mathrm{d}n}{\mathrm{d}\Omega} \right) σ ( θ , φ ) = j i 1 ( d Ω d n )
其量纲为面积,一般用单位 barn \text{barn} barn 1 barn = 1 0 − 28 m 2 1 \text{barn} = 10^{-28} \text{m}^2 1 barn = 1 0 − 28 m 2 总截面
σ t = ∫ σ ( θ , φ ) d Ω = ∫ 0 2 π d φ ∫ 0 π d θ sin θ σ ( θ , φ ) \sigma_t = \int \sigma(\theta,\varphi) \mathrm{d}\Omega = \int_{0}^{2\pi} \mathrm{d}\varphi \int_{0}^{\pi} \mathrm{d}\theta \sin\theta\ \sigma(\theta,\varphi) σ t = ∫ σ ( θ , φ ) d Ω = ∫ 0 2 π d φ ∫ 0 π d θ sin θ σ ( θ , φ )
假定靶粒子与入射粒子的相互作用是中心势 V ( r ⃗ ) V(\vec{r}) V ( r )
取入射方向为 z z z 平面波
ψ i = e i k z \psi_i = \mathrm{e}^{\mathrm{i}kz} ψ i = e i k z
它是动量的本征态 , p z = ℏ k , p x = p y = 0 p_z = \hbar k ,\ p_x = p_y = 0 p z = ℏ k , p x = p y = 0 E = ℏ 2 k 2 2 μ E = \frac{\hbar^2k^2}{2\mu} E = 2 μ ℏ 2 k 2 j i = ℏ k μ j_i = \frac{\hbar k}{\mu} j i = μ ℏ k
和靶粒子对入射粒子的作用区域相比,放置探测器的位置可以认为是无限远,在渐近条件 r → ∞ r\to\infty r → ∞ V ( r ⃗ ) V(\vec{r}) V ( r ) ψ s \psi_s ψ s φ \varphi φ
ψ s = f ( θ ) e i k r r \psi_s = f(\theta) \frac{\mathrm{e}^{\mathrm{i}kr}}{r} ψ s = f ( θ ) r e i k r
综上,在 r → ∞ r\to\infty r → ∞ ψ i \psi_i ψ i ψ s \psi_s ψ s
lim r → ∞ ψ = e i k z + f ( θ ) e i k r r \lim_{r\to\infty} \psi = \mathrm{e}^{\mathrm{i}kz} + f(\theta) \frac{\mathrm{e}^{\mathrm{i}kr}}{r} r → ∞ lim ψ = e i k z + f ( θ ) r e i k r
设相互作用为 V ( r ⃗ ) V(\vec{r}) V ( r )
{ [ − ℏ 2 2 μ ∇ 2 + V ( r ⃗ ) ] ψ = E ψ lim r → ∞ ψ = e i k z + f ( θ ) e i k r r \begin{cases} \left[ -\frac{\hbar^2}{2\mu} \nabla^2 + V(\vec{r}) \right] \psi = E \psi \ \lim_{r\to\infty} \psi = \mathrm{e}^{\mathrm{i}kz} + f(\theta) \frac{\mathrm{e}^{\mathrm{i}kr}}{r} \end{cases} { [ − 2 μ ℏ 2 ∇ 2 + V ( r ) ] ψ = E ψ lim r → ∞ ψ = e i k z + f ( θ ) r e i k r
只要在能量取确定值 E = ℏ 2 k 2 2 μ E = \frac{\hbar^2k^2}{2\mu} E = 2 μ ℏ 2 k 2 ψ \psi ψ ψ \psi ψ r → ∞ r\to\infty r → ∞ 散射波幅
f ( θ ) = lim r → ∞ r e − i k z ( ψ − e i k r ) f(\theta) = \lim_{r\to\infty} r \mathrm{e}^{-\mathrm{i}kz} \left( \psi - \mathrm{e}^{\mathrm{i}kr} \right) f ( θ ) = r → ∞ lim r e − i k z ( ψ − e i k r )
通过散射波幅,可以计算散射粒子流密度
j s = i ℏ 2 μ ( ψ ∂ ∂ r ψ ∗ − ψ ∗ ∂ ∂ r ψ ) = ℏ k μ ∣ f ( θ ) ∣ 2 r 2 j_s = \frac{\mathrm{i}\hbar}{2\mu} \left( \psi \frac{\partial}{\partial r} \psi^* - \psi^* \frac{\partial}{\partial r} \psi \right) = \frac{\hbar k}{\mu} \frac{|f(\theta)|^2}{r^2} j s = 2 μ i ℏ ( ψ ∂ r ∂ ψ ∗ − ψ ∗ ∂ r ∂ ψ ) = μ ℏ k r 2 ∣ f ( θ ) ∣ 2
散射截面
σ ( θ ) = 1 j i ( d n d Ω ) = 1 j i j s r 2 d Ω d Ω = ∣ f ( θ ) ∣ 2 \sigma(\theta) = \frac{1}{j_i} \left( \frac{\mathrm{d}n}{\mathrm{d}\Omega} \right) = \frac{1}{j_i} \frac{j_s r^2 \mathrm{d}\Omega}{\mathrm{d}\Omega}\ = |f(\theta)|^2 σ ( θ ) = j i 1 ( d Ω d n ) = j i 1 d Ω j s r 2 d Ω = ∣ f ( θ ) ∣ 2
记在质心系中的散射角为 θ C \theta_C θ C θ L \theta_L θ L m m m M M M
tan θ L = sin θ C γ + cos θ C , γ = m M \tan \theta_L = \frac{\sin\theta_C}{\gamma + \cos \theta_C} , \kern 2em \gamma = \frac{m}{M} tan θ L = γ + cos θ C sin θ C , γ = M m
截面的变换关系为
σ ( θ L ) = ( 1 + 2 γ cos θ C + γ 2 ) 3 2 ∣ 1 + γ cos θ C ∣ σ ( θ C ) \sigma(\theta_L) = \frac{(1 + 2\gamma\cos\theta_C + \gamma^2)^{\frac32}}{|1 + \gamma\cos\theta_C|} \sigma(\theta_C) σ ( θ L ) = ∣1 + γ cos θ C ∣ ( 1 + 2 γ cos θ C + γ 2 ) 2 3 σ ( θ C )
当能量 E = ℏ 2 k 2 2 μ E = \frac{\hbar^2k^2}{2\mu} E = 2 μ ℏ 2 k 2
{ [ − ℏ 2 2 μ ∇ 2 + V ( r ⃗ ) ] ψ = E ψ lim r → ∞ ψ = e i k z + f ( θ ) e i k r r ⇕ { ( ∇ 2 + k 2 ) ψ ( r ⃗ ) = 2 μ ℏ 2 V ( r ⃗ ) ψ ( r ⃗ ) lim r → ∞ ψ = e i k z + f ( θ ) e i k r r \begin{cases} \left[ -\frac{\hbar^2}{2\mu} \nabla^2 + V(\vec{r}) \right] \psi = E \psi \ \lim_{r\to\infty} \psi = \mathrm{e}^{\mathrm{i}kz} + f(\theta) \frac{\mathrm{e}^{\mathrm{i}kr}}{r} \end{cases} \ \Updownarrow \ \begin{cases} (\nabla^2 + k^2) \psi(\vec{r}) = \frac{2\mu}{\hbar^2} V(\vec{r}) \psi(\vec{r}) \ \lim_{r\to\infty} \psi = \mathrm{e}^{\mathrm{i}kz} + f(\theta) \frac{\mathrm{e}^{\mathrm{i}kr}}{r} \end{cases} { [ − 2 μ ℏ 2 ∇ 2 + V ( r ) ] ψ = E ψ lim r → ∞ ψ = e i k z + f ( θ ) r e i k r ⇕ { ( ∇ 2 + k 2 ) ψ ( r ) = ℏ 2 2 μ V ( r ) ψ ( r ) lim r → ∞ ψ = e i k z + f ( θ ) r e i k r
的求解,定义Green函数 G ( r ⃗ , r ⃗ ′ ) G(\vec{r},\vec{r}') G ( r , r ′ )
( ∇ 2 + k 2 ) G ( r ⃗ , r ⃗ ′ ) = δ ( r ⃗ − r ⃗ ′ ) (\nabla^2 + k^2) G(\vec{r},\vec{r}') = \delta(\vec{r}-\vec{r}') ( ∇ 2 + k 2 ) G ( r , r ′ ) = δ ( r − r ′ )
则方程的解可以表示为
ψ ( r ⃗ ) = ψ ( 0 ) ( r ⃗ ) + 2 μ ℏ 2 ∫ d 3 r ′ G ( r ⃗ , r ⃗ ′ ) V ( r ⃗ ′ ) ψ ( r ⃗ ′ ) \psi(\vec{r}) = \psi^{(0)}(\vec{r}) + \frac{2\mu}{\hbar^2} \int \mathrm{d}^3r'\ G(\vec{r},\vec{r}')\ V(\vec{r}')\ \psi(\vec{r}') ψ ( r ) = ψ ( 0 ) ( r ) + ℏ 2 2 μ ∫ d 3 r ′ G ( r , r ′ ) V ( r ′ ) ψ ( r ′ )
其中 ψ ( 0 ) ( r ⃗ ) \psi^{(0)}(\vec{r}) ψ ( 0 ) ( r )
( ∇ 2 + k 2 ) ψ ( 0 ) ( r ⃗ ) = 0 (\nabla^2 + k^2) \psi^{(0)}(\vec{r}) = 0 ( ∇ 2 + k 2 ) ψ ( 0 ) ( r ) = 0
若假设入射波为 ψ i ( r ⃗ ) = e i k ⃗ ⋅ r ⃗ \psi_i(\vec{r}) = \mathrm{e}^{\mathrm{i}\vec{k}\cdot\vec{r}} ψ i ( r ) = e i k ⋅ r ψ ( 0 ) ( r ⃗ ) \psi^{(0)}(\vec{r}) ψ ( 0 ) ( r ) ψ i ( r ⃗ ) \psi_i(\vec{r}) ψ i ( r ) Lippman-Schwinger方程
ψ ( r ⃗ ) = e i k ⃗ ⋅ r ⃗ + 2 μ ℏ 2 ∫ d 3 r ′ G ( r ⃗ , r ⃗ ′ ) V ( r ⃗ ′ ) ψ ( r ⃗ ′ ) = ψ i ( r ⃗ ) + ψ s c ( r ⃗ ) \psi(\vec{r}) = \mathrm{e}^{\mathrm{i}\vec{k}\cdot\vec{r}} + \frac{2\mu}{\hbar^2} \int \mathrm{d}^3r'\ G(\vec{r},\vec{r}')\ V(\vec{r}')\ \psi(\vec{r}') \ \ \ = \psi_i(\vec{r}) + \psi_{sc}(\vec{r}) ψ ( r ) = e i k ⋅ r + ℏ 2 2 μ ∫ d 3 r ′ G ( r , r ′ ) V ( r ′ ) ψ ( r ′ ) = ψ i ( r ) + ψ sc ( r )
Green函数的求解结果为
G ( r ⃗ , r ⃗ ′ ) = − e i k ∣ r ⃗ − r ⃗ ′ ∣ 4 π ∣ r ⃗ − r ⃗ ′ ∣ G(\vec{r},\vec{r}') = -\frac{\mathrm{e}^{\mathrm{i}k|\vec{r}-\vec{r}'|}}{4\pi|\vec{r}-\vec{r}'|} G ( r , r ′ ) = − 4 π ∣ r − r ′ ∣ e i k ∣ r − r ′ ∣
代入可得
ψ ( r ⃗ ) = e i k ⃗ ⋅ r ⃗ − μ 2 π ℏ 2 ∫ d 3 r ′ e i k ∣ r ⃗ − r ⃗ ′ ∣ ∣ r ⃗ − r ⃗ ′ ∣ V ( r ⃗ ′ ) ψ ( r ⃗ ′ ) \psi(\vec{r}) = \mathrm{e}^{\mathrm{i}\vec{k}\cdot\vec{r}} - \frac{\mu}{2\pi\hbar^2} \int \mathrm{d}^3r'\ \frac{\mathrm{e}^{\mathrm{i}k|\vec{r}-\vec{r}'|}}{|\vec{r}-\vec{r}'|}\ V(\vec{r}')\ \psi(\vec{r}') ψ ( r ) = e i k ⋅ r − 2 π ℏ 2 μ ∫ d 3 r ′ ∣ r − r ′ ∣ e i k ∣ r − r ′ ∣ V ( r ′ ) ψ ( r ′ )
具体求解时往往只能采取逐级近似法。
Born近似主要适用于高能粒子散射。
记 q = 2 k sin ( θ / 2 ) q = 2k\sin(\theta/2) q = 2 k sin ( θ /2 ) V V V
f ( θ ) = − 2 μ ℏ 2 q ∫ 0 ∞ r ′ V ( r ′ ) sin ( q r ′ ) d r ′ σ ( θ ) = ∣ f ( θ ) ∣ 2 = 4 μ 2 ℏ 4 q 2 ∣ ∫ 0 ∞ r ′ V ( r ′ ) sin ( q r ′ ) d r ′ ∣ 2 f(\theta) = -\frac{2\mu}{\hbar^2q} \int_0^\infty r' V(r') \sin(qr') \mathrm{d}r' \ \ \ \sigma(\theta) = |f(\theta)|^2 = \frac{4\mu^2}{\hbar^4q^2} \left| \int_0^\infty r' V(r') \sin(qr') \mathrm{d}r' \right|^2 f ( θ ) = − ℏ 2 q 2 μ ∫ 0 ∞ r ′ V ( r ′ ) sin ( q r ′ ) d r ′ σ ( θ ) = ∣ f ( θ ) ∣ 2 = ℏ 4 q 2 4 μ 2 ∫ 0 ∞ r ′ V ( r ′ ) sin ( q r ′ ) d r ′ 2
考虑粒子在 V ( r ) = A r V(r) = \frac{A}{r} V ( r ) = r A
f ( θ ) = − 2 μ ℏ 2 q ∫ 0 ∞ r ′ V ( r ′ ) sin ( q r ′ ) d r ′ = − 2 μ ℏ 2 q ∫ 0 ∞ r ′ A r ′ sin ( q r ′ ) d r ′ = − 2 μ A ℏ 2 q ∫ 0 ∞ sin ( q r ′ ) d r ′ f(\theta) = -\frac{2\mu}{\hbar^2q} \int_0^\infty r' V(r') \sin(qr') \mathrm{d}r' \ \ \ = -\frac{2\mu}{\hbar^2q} \int_0^\infty r'\frac{A}{r'} \sin(qr') \mathrm{d}r' \ \ \ = -\frac{2\mu A}{\hbar^2q} \int_0^\infty \sin(qr') \mathrm{d}r' f ( θ ) = − ℏ 2 q 2 μ ∫ 0 ∞ r ′ V ( r ′ ) sin ( q r ′ ) d r ′ = − ℏ 2 q 2 μ ∫ 0 ∞ r ′ r ′ A sin ( q r ′ ) d r ′ = − ℏ 2 q 2 μ A ∫ 0 ∞ sin ( q r ′ ) d r ′
由于此积分发散,引入衰减因子 e − ε r ′ ( ε > 0 ) \mathrm{e}^{-\varepsilon r'}\ (\varepsilon>0) e − ε r ′ ( ε > 0 ) ε → 0 \varepsilon \to 0 ε → 0
f ( θ ) = lim ε → 0 − 2 μ A ℏ 2 q ∫ 0 ∞ sin ( q r ′ ) e − ε r ′ d r ′ = − 2 μ A ℏ 2 q lim ε → 0 q ε 2 + q 2 = − 2 μ A ℏ 2 q 2 f(\theta) = \lim_{\varepsilon \to 0} -\frac{2\mu A}{\hbar^2q} \int_0^\infty \sin(qr') \mathrm{e}^{-\varepsilon r'} \mathrm{d}r' \ \ \ = -\frac{2\mu A}{\hbar^2q} \lim_{\varepsilon \to 0} \frac{q}{\varepsilon^2+q^2} \ \ \ = -\frac{2\mu A}{\hbar^2q^2} f ( θ ) = ε → 0 lim − ℏ 2 q 2 μ A ∫ 0 ∞ sin ( q r ′ ) e − ε r ′ d r ′ = − ℏ 2 q 2 μ A ε → 0 lim ε 2 + q 2 q = − ℏ 2 q 2 2 μ A
故散射截面为
σ ( θ ) = ∣ f ( θ ) ∣ 2 = 4 μ 2 A 2 ℏ 4 q 4 = A 2 4 μ 2 v 4 sin 4 θ 2 \sigma(\theta) = |f(\theta)|^2 = \frac{4\mu^2A^2}{\hbar^4q^4} = \frac{A^2}{4\mu^2v^4\sin^4\frac{\theta}{2}} σ ( θ ) = ∣ f ( θ ) ∣ 2 = ℏ 4 q 4 4 μ 2 A 2 = 4 μ 2 v 4 sin 4 2 θ A 2
此即Rutherford散射公式。
电子和原子散射时,入射电子除了受原子核库仑引力作用外,还受核外诸电子库仑斥力的作用。严格说,这是一个多体问题,但如果将核外各个电子的作用近似为一个分布电荷 − e ρ ( r ⃗ ) -e\rho(\vec{r}) − e ρ ( r )
V ( r ⃗ ) = − Z e 2 r + e 2 ∫ ρ ( r ⃗ ′ ) r ⃗ − r ⃗ ′ d r ⃗ ′ V(\vec{r}) = -\frac{Ze^2}{r} + e^2 \int \frac{\rho(\vec{r}')}{\vec{r}-\vec{r}'} \mathrm{d}\vec{r}' V ( r ) = − r Z e 2 + e 2 ∫ r − r ′ ρ ( r ′ ) d r ′
则
f ( θ , φ ) = − μ 2 π ℏ 2 ∫ d r ⃗ ′ e − i q ⃗ ⋅ r ⃗ ′ V ( r ⃗ ′ ) = − μ 2 π ℏ 2 ∫ d r ⃗ ′ e − i q ⃗ ⋅ r ⃗ ′ [ − Z e 2 r ′ + e 2 ∫ ρ ( r ⃗ ′ ′ ) r ⃗ ′ − r ⃗ ′ ′ d r ⃗ ′ ′ ] = μ e 2 2 π ℏ 2 [ 4 π Z q 2 − 4 π q 2 ∫ ρ ( r ⃗ ′ ′ ) e − i q ⃗ ⋅ r ⃗ ′ ′ d r ⃗ ′ ′ ] f(\theta,\varphi) = -\frac{\mu}{2\pi\hbar^2} \int \mathrm{d}\vec{r}'\ \mathrm{e}^{-\mathrm{i}\vec{q}\cdot\vec{r}'} V(\vec{r}') \ \ \ = -\frac{\mu}{2\pi\hbar^2} \int \mathrm{d}\vec{r}'\ \mathrm{e}^{-\mathrm{i}\vec{q}\cdot\vec{r}'} \left[ -\frac{Ze^2}{r'} + e^2 \int \frac{\rho(\vec{r}'')}{\vec{r}'-\vec{r}''} \mathrm{d}\vec{r}'' \right] \ \ \ = \frac{\mu e^2}{2\pi\hbar^2} \left[ \frac{4\pi Z}{q^2} - \frac{4\pi}{q^2} \int \rho(\vec{r}'') \mathrm{e}^{-\mathrm{i}\vec{q}\cdot\vec{r}''} \mathrm{d}\vec{r}'' \right] f ( θ , φ ) = − 2 π ℏ 2 μ ∫ d r ′ e − i q ⋅ r ′ V ( r ′ ) = − 2 π ℏ 2 μ ∫ d r ′ e − i q ⋅ r ′ [ − r ′ Z e 2 + e 2 ∫ r ′ − r ′′ ρ ( r ′′ ) d r ′′ ] = 2 π ℏ 2 μ e 2 [ q 2 4 π Z − q 2 4 π ∫ ρ ( r ′′ ) e − i q ⋅ r ′′ d r ′′ ]
记Born近似下的弹性散射形状因子(form factor)为
F ( θ , φ ) = ∫ ρ ( r ⃗ ′ ′ ) e − i q ⃗ ⋅ r ⃗ ′ ′ d r ⃗ ′ ′ F(\theta,\varphi) = \int \rho(\vec{r}'') \mathrm{e}^{-\mathrm{i}\vec{q}\cdot\vec{r}''} \mathrm{d}\vec{r}'' F ( θ , φ ) = ∫ ρ ( r ′′ ) e − i q ⋅ r ′′ d r ′′
则
f ( θ , φ ) = 2 μ e 2 ℏ 2 q 2 [ Z − F ( θ , φ ) ] = 2 μ e 2 ℏ 2 q 2 Z e f f σ ( θ , φ ) = ∣ f ( θ , φ ) ∣ 2 = 4 μ 2 e 4 ℏ 4 q 4 Z e f f 2 = μ 2 e 4 Z e f f 2 4 ℏ 4 k 4 sin 4 θ 2 f(\theta,\varphi) = \frac{2\mu e^2}{\hbar^2q^2} \left[ Z - F(\theta,\varphi) \right] = \frac{2\mu e^2}{\hbar^2q^2} Z_{eff} \ \ \ \sigma(\theta,\varphi) = |f(\theta,\varphi)|^2 = \frac{4\mu^2e^4}{\hbar^4q^4} Z_{eff}^2 = \frac{\mu^2e^4Z_{eff}^2}{4\hbar^4k^4\sin^4\frac{\theta}{2}} f ( θ , φ ) = ℏ 2 q 2 2 μ e 2 [ Z − F ( θ , φ ) ] = ℏ 2 q 2 2 μ e 2 Z e ff σ ( θ , φ ) = ∣ f ( θ , φ ) ∣ 2 = ℏ 4 q 4 4 μ 2 e 4 Z e ff 2 = 4 ℏ 4 k 4 sin 4 2 θ μ 2 e 4 Z e ff 2
此部分内容不作为考试要求
分波法主要适用于低能粒子散射。
该部分内容亦可参考核反应中的分波分析
求解径向方程
[ 1 r d 2 d r 2 r + 2 m ℏ 2 ( E − V ( r ) ) − l ( l + 1 ) r 2 ] R l ( r ) = 0 \left[ \frac{1}{r}\frac{\mathrm{d}^2}{\mathrm{d}r^2}r + \frac{2m}{\hbar^2}\left(E-V(r)\right) - \frac{l(l+1)}{r^2} \right] R_l(r) = 0 [ r 1 d r 2 d 2 r + ℏ 2 2 m ( E − V ( r ) ) − r 2 l ( l + 1 ) ] R l ( r ) = 0
当 r → ∞ r\to\infty r → ∞ R l ( r ) R_l(r) R l ( r )
lim r → ∞ R l ( r ) = B l k r sin ( k r − l π 2 + δ l ) \lim_{r\to\infty} R_l(r) = \frac{B_l}{kr} \sin(kr - \frac{l\pi}{2} + \delta_l) r → ∞ lim R l ( r ) = k r B l sin ( k r − 2 l π + δ l )
其中 k = 2 m E ℏ k = \frac{\sqrt{2mE}}{\hbar} k = ℏ 2 m E δ l \delta_l δ l l l l 相移 ,通常根据边界条件求得。
第 l l l 散射截面
σ l = 4 π k 2 ( 2 l + 1 ) sin 2 δ l \sigma_l = \frac{4\pi}{k^2} (2l+1) \sin^2\delta_l σ l = k 2 4 π ( 2 l + 1 ) sin 2 δ l
总截面
σ t = ∑ l = 0 ⌊ k a ⌋ σ l \sigma_t = \sum_{l=0}^{\lfloor ka \rfloor} \sigma_l σ t = l = 0 ∑ ⌊ ka ⌋ σ l
其中 a a a
以下讨论均忽略掉 R l ( r ) R_l(r) R l ( r )
当 V ( r ) = − V 0 V(r) = -V_0 V ( r ) = − V 0 k 1 = 2 m ( E + V 0 ) ℏ k_1 = \frac{\sqrt{2m(E+V_0)}}{\hbar} k 1 = ℏ 2 m ( E + V 0 )
R l ( r ) = cos δ l j l ( k 1 r ) − sin δ l n l ( k 1 r ) R_l(r) = \cos\delta_l\ \mathrm{j}_l(k_1r) - \sin\delta_l\ \mathrm{n}_l(k_1r) R l ( r ) = cos δ l j l ( k 1 r ) − sin δ l n l ( k 1 r )
此时当 k → ∞ k \to \infty k → ∞
R l ( r ) → 1 k 1 r [ cos δ l sin ( k 1 r − l π 2 ) + sin δ l cos ( k 1 r − l π 2 ) ] = 1 k 1 r sin ( k 1 r − l π 2 + δ l ) R_l(r) \to \frac{1}{k_1r} \left[ \cos\delta_l\ \sin\left(k_1r-\frac{l\pi}{2}\right) + \sin\delta_l\ \cos\left(k_1r-\frac{l\pi}{2}\right) \right] \ \ \ = \frac{1}{k_1r} \sin\left(k_1r-\frac{l\pi}{2}+\delta_l\right) R l ( r ) → k 1 r 1 [ cos δ l sin ( k 1 r − 2 l π ) + sin δ l cos ( k 1 r − 2 l π ) ] = k 1 r 1 sin ( k 1 r − 2 l π + δ l )
进一步的,当 l = 0 l=0 l = 0 k → ∞ k\to\infty k → ∞ s s s
R l ( r ) = 1 k 1 r [ cos δ l sin ( k 1 r ) + sin δ l cos ( k 1 r ) ] = 1 k 1 r sin ( k 1 r + δ l ) R_l(r) = \frac{1}{k_1r} \left[ \cos\delta_l\ \sin\left(k_1r\right) + \sin\delta_l\ \cos\left(k_1r\right) \right] \ \ \ = \frac{1}{k_1r} \sin\left(k_1r+\delta_l\right) R l ( r ) = k 1 r 1 [ cos δ l sin ( k 1 r ) + sin δ l cos ( k 1 r ) ] = k 1 r 1 sin ( k 1 r + δ l )
球Bessel函数
j l ( x ) = ( − 1 ) l x l ( 1 x d d x ) l sin x x \mathrm{j}_l(x) = (-1)^l x^l \left( \frac{1}{x} \frac{\mathrm{d}}{\mathrm{d}x} \right)^l \frac{\sin x}{x} j l ( x ) = ( − 1 ) l x l ( x 1 d x d ) l x sin x
球Neumann函数
n l ( x ) = ( − 1 ) l + 1 x l ( 1 x d d x ) l cos x x \mathrm{n}_l(x) = (-1)^{l+1} x^l \left( \frac{1}{x} \frac{\mathrm{d}}{\mathrm{d}x} \right)^l \frac{\cos x}{x} n l ( x ) = ( − 1 ) l + 1 x l ( x 1 d x d ) l x cos x
最简单的几个如下
j 0 ( x ) = sin x x , j 1 ( x ) = sin x x 2 − cos x x n 0 ( x ) = − cos x x , n 1 ( x ) = − cos x x 2 − sin x x \mathrm{j}_0(x) = \frac{\sin x}{x} , \kern 2em \mathrm{j}_1(x) = \frac{\sin x}{x^2} - \frac{\cos x}{x} \ \ \ \mathrm{n}_0(x) = -\frac{\cos x}{x} , \kern 2em \mathrm{n}_1(x) = -\frac{\cos x}{x^2} - \frac{\sin x}{x} j 0 ( x ) = x sin x , j 1 ( x ) = x 2 sin x − x cos x n 0 ( x ) = − x cos x , n 1 ( x ) = − x 2 cos x − x sin x
x → 0 x\to0 x → 0
j l ( x ) ≈ x l ( 2 l + 1 ) ! ! n l ( x ) ≈ − ( 2 l − 1 ) ! ! x l + 1 \mathrm{j}_l(x) \approx \frac{x^l}{(2l+1)!!} \ \ \ \mathrm{n}_l(x) \approx -\frac{(2l-1)!!}{x^{l+1}} j l ( x ) ≈ ( 2 l + 1 )!! x l n l ( x ) ≈ − x l + 1 ( 2 l − 1 )!!
x → ∞ x\to\infty x → ∞
j l ( x ) ≈ 1 x sin ( x − l π 2 ) n l ( x ) ≈ − 1 x cos ( x − l π 2 ) \mathrm{j}_l(x) \approx \frac{1}{x} \sin\left(x-\frac{l\pi}{2}\right) \ \ \ \mathrm{n}_l(x) \approx -\frac{1}{x} \cos\left(x-\frac{l\pi}{2}\right) j l ( x ) ≈ x 1 sin ( x − 2 l π ) n l ( x ) ≈ − x 1 cos ( x − 2 l π )
在高能时
δ l = − 2 m k ℏ 2 ∫ 0 + ∞ V ( r ) j l 2 ( k r ) r 2 d r \delta_l = -\frac{2mk}{\hbar^2} \int_{0}^{+\infty} V(r)\ \mathrm{j}_l^2(kr)\ r^2 \mathrm{dr} δ l = − ℏ 2 2 mk ∫ 0 + ∞ V ( r ) j l 2 ( k r ) r 2 dr
其中 k = 2 m E ℏ k = \frac{\sqrt{2mE}}{\hbar} k = ℏ 2 m E
解答仅供参考!
β稳定曲线为什么刚开始与 Z=N 的直线重合?为什么后来又偏离了这个直线,向哪个方向偏离?β稳定曲线会不会向高 A 区无限延伸?
不会,高A区的库仑排斥太大,但核力是短程力,具有饱和性。而核子数量增大会使得比结合能变小,核子间结合得比较松散。
如何由“原子核有确定的宇称”,推出“其电偶极矩必然为 0”的结论?对于电四极矩可以有如此明确的断言吗?
质量过剩描述的对象是谁?辨析它和质量亏损这个概念的区别。
原子。
质量过剩是原子的质量与 A u Au A u
随着核子数 A 的增大,液滴模型中几个比结合能项会分别怎么变化?液滴模型有什么不足之处吗?
ε = a V − a S A 1 / 3 − a C Z 2 A 4 / 3 − a s y m ( A / 2 − Z ) 2 A 2 + δ a p A 3 / 2 \varepsilon = a_V - \frac{a_S}{A^{1/3}} - \frac{a_CZ^2}{A^{4/3}} - \frac{a_{sym}(A/2 - Z)^2}{A^2} + \frac{\delta a_p}{A^{3/2}} ε = a V − A 1/3 a S − A 4/3 a C Z 2 − A 2 a sy m ( A /2 − Z ) 2 + A 3/2 δ a p
原子核从基态来到某个激发态时,统计性、宇称、磁矩、电四极矩会发生变化吗,为什么?
统计性不会变化:费米子,玻色子只和 A A A
宇称可能变化:内部核子的轨道角动量发生变化;
磁矩可能变化:内部核子的轨道角动量改变,磁矩改变;
电四极矩可能,激发态原子核形状可能发生变化。
如何理解核力的“自旋-轨道耦合”项对于壳层结构幻数的意义?
核力的自旋-轨道耦合很强,使得l>0的能级都一分为二,并且两个能级的间距可以很大,显示了清晰的壳层结构,组成了新的原子核壳层结构并给出了全部幻数。
在什么情况下,原子核被探测器测量出的半衰期和自己实际的半衰期是不同的?如何快速估计放射平衡的达成时间?
发生递次衰变,暂时平衡或长期平衡的子核,测得的是母核的半衰期。
是较小的半衰期的几到十几倍。
放射源的制备问题
影响其活度的 5 个因素分别是什么
A ( t ) = N t σ Φ ( 1 − e − λ t ) A(t) = N_t \sigma \Phi (1-\mathrm{e}^{-\lambda t}) A ( t ) = N t σ Φ ( 1 − e − λ t )
N t N_t N t σ \sigma σ Φ \Phi Φ
为了高的活度,无限地延长照射时间,是否合理?
不合理,达到一定时间后,活度很接近1,再照射意义不大,六七倍半衰期即可满足要求。
若为了获得最大活度的 75%,需要照射多久?
两个半衰期。
说出至少两种测量核素半衰期的方法?(扩展阅读第二章阅读材料 2)
直接测量:适用于半衰期在几分钟到几小时内的衰变。直接观察活度随时间的指数衰减,作图 ln A ∼ t \ln A \sim t ln A ∼ t
比活度法(比活度,单位物质的活度量):适用于非常长的半衰期,此时 N N N A = λ N A=\lambda N A = λ N A A A N N N
延迟符合技术:使用时间幅度转化器TAC测量,先用母核产生子核与一个小粒子,小粒子用于标定开始时间,然后可以测得子核衰变放出的粒子,从而确定子核的寿命。
多道分析法:适用于半衰期小于几分钟的衰变。利用多道分析仪内建的多重计时功能,接受一个逻辑脉冲而不是线性脉冲,通过设置变量的驻留时间来适应快速的衰变过程。
多普勒反冲法:适用于 1 0 − 10 ∼ 1 0 − 12 s 10^{-10} \sim 10^{-12} \text{s} 1 0 − 10 ∼ 1 0 − 12 s γ \gamma γ γ \gamma γ γ \gamma γ γ \gamma γ
工作中常用的 γ 源(如 137Cs 或 60Co)不大可能是单纯的 γ 源,而通常也是个 β 源,为什么?(可结合第三章内容)。
绝对强度、分支比,以及第三章的内转换系数,都是无量纲数,它们的物理意义是什么?
绝对强度是针对衰变纲图中的主核素来说的,它就是衰变纲图中的百分数,其意义:主核素衰变时某粒子出射或衰变途径发生的概率是多少。
分支比则是针对衰变纲图中的某个具体核素(可以是主核素,也可以是子核素)的,分支衰变对应于哪个核素,分支比就是哪个核素的。
内转换系数 α = λ e λ γ \alpha = \frac{\lambda_e}{\lambda_\gamma} α = λ γ λ e
针对 α 衰变、β 衰变和 γ 跃迁,解释衰变能、角动量、宇称这三个量对其衰变过程的影响。
衰变能大、放出的粒子带走的角动量小,衰变更容易发生,宇称与角动量一起对衰变进行选择。
对于 α \alpha α α \alpha α α \alpha α π i = π f π α = π f ( − 1 ) l \pi_i = \pi_f \pi_\alpha = \pi_f (-1)^{l} π i = π f π α = π f ( − 1 ) l 0 0 0 π α = ( − 1 ) Δ I \pi_\alpha = (-1)^{\Delta I} π α = ( − 1 ) Δ I
对于 β \beta β λ ∝ E 5 \lambda \propto E^5 λ ∝ E 5 E E E l l l ( k r ) l (kr)^l ( k r ) l β \beta β π i = π f ( − 1 ) l \pi_i = \pi_f (-1)^l π i = π f ( − 1 ) l β \beta β
对于 γ \gamma γ λ ∝ E γ 2 L + 1 \lambda \propto E_{\gamma}^{2L+1} λ ∝ E γ 2 L + 1 λ ∝ ( k R ) 2 L \lambda \propto (kR)^{2L} λ ∝ ( k R ) 2 L γ \gamma γ π i = π f π γ \pi_i = \pi_f \pi_\gamma π i = π f π γ π γ = ( − 1 ) l \pi_\gamma = (-1)^l π γ = ( − 1 ) l π γ = ( − 1 ) l + 1 \pi_\gamma = (-1)^{l+1} π γ = ( − 1 ) l + 1 γ \gamma γ
试着定性说明为什么在 α 衰变中,衰变能一般在约 4~9MeV 之间,既不会很大,也不会很小?
因为 α \alpha α 20 ∼ 30 Mev 20 \sim 30 \text{Mev} 20 ∼ 30 Mev α \alpha α α \alpha α
讨论一下在 α 衰变、β 衰变和 γ 跃迁过程可能产生的粒子(提示:各衰变后续过程产生的粒子也应尽可能考虑)。
不带电的粒子
带电的粒子
能量取分立值的粒子
能量呈现连续分布的粒子
不带电的粒子:ν e , ν ~ e , γ , X \nu_e , \widetilde{\nu}_e , \gamma , X ν e , ν e , γ , X
α \alpha α β \beta β β + , β − \beta^+,\beta^- β + , β − ν e , ν ~ e \nu_e , \widetilde{\nu}_e ν e , ν e X X X γ \gamma γ γ \gamma γ X X X
带电的粒子: α , e − , e + \alpha , e^- , e^+ α , e − , e +
α \alpha α α \alpha α β \beta β β + , β − \beta^+,\beta^- β + , β − e + , e − e^+,e^- e + , e − γ \gamma γ
能量取分立值的粒子: α , ν e , γ \alpha , \nu_e , \gamma α , ν e , γ X X X
α \alpha α α \alpha α β \beta β ν e \nu_e ν e X X X γ \gamma γ γ \gamma γ X X X
能量呈现连续分布的粒子: e + , e − , ν e , ν ~ e e^+,e^-,\nu_e,\widetilde{\nu}_e e + , e − , ν e , ν e
α \alpha α β \beta β β + , β − \beta^+,\beta^- β + , β − e + , e − , ν e , ν ~ e e^+,e^-,\nu_e,\widetilde{\nu}_e e + , e − , ν e , ν e γ \gamma γ
跃迁矩阵元对于 β 衰变的衰变常数影响很大的原因是什么?
(略,参照 β \beta β
请解释一下β衰变的选择定则的形成过程
(略,参照课本课件)
请解释一下γ跃迁的选择定则的形成过程?
(略,参照课本课件)
既然原子核的电偶极矩必然为 0,为什么γ跃迁的电偶极跃迁仍可能是存在的,而且(如果存在的话)是最强的?
电偶极矩与电偶极辐射概念不同。
(略,参照 γ \gamma γ
把(由 Z 个质子、N 个中子构成的)原子核的每一个能级都用一条线画出来,线的宽度代表了能级宽度 Γ。
如果只允许其中一条线的宽度为 0,则这条线会对应哪个能级?
对于该原子核,1.所述的宽度为 0 的线一定存在吗,为什么?
一般来说,能级越高,线的宽度是越大还是越小,为什么?
基态。
不一定存在,因为基态不一定稳定。
越大,因为能级越高,衰变越快,线宽越大。
解答仅供参考!
在测量 γ \gamma γ γ \gamma γ 1.33 MeV 1.33\text{MeV} 1.33 MeV
γ \gamma γ
最后一步反应是光电效应:
光子能量逐渐降低,而在低能区光电效应截面最大;
当能量小于 1.022 MeV 1.022\text{MeV} 1.022 MeV
电子对效应与康普顿散射都会产生光子,还需要后续反应进行能量沉积。
核辐射测量过程的各个环节都包含有随机性。例如:我们在测量活度时,放射源中每个原子核的衰变都是独立而随机的,那我们为什么又可以言之凿凿地说“测得某源的活度是多少多少”呢?又如:带电粒子在探测器介质内的电离过程是随机的,产生的载流子数目并不确定,每个载流子的产生都是随机的,可是为什么我们最终又能够以很好的分辨率(如半导体探测器)来形成全能峰呢?简而言之,微观过程总是难以免除随机性,那么宏观过程是如何变得越来越确定呢?
在实验测量过程中,客观性存在偶然误差,但是偶然误差可以发现与消除,利用大量的实验数据,可以实现对偶然误差的统计分析。即“‘确定’的大厦,构建于‘不确定’的砖块”。
在众多随机变量堆叠而成新变量的过程中:不确定性在以0.5次方增长,其确定性在以1次方增长,且确定性增长地更快, ν ∝ 1 N \nu \propto \frac{1}{\sqrt{N}} ν ∝ N 1
γ \gamma γ 511 keV 511\text{keV} 511 keV 511 keV 511\text{keV} 511 keV γ \gamma γ 1.022 MeV 1.022\text{MeV} 1.022 MeV
因为正负电子湮没主要是两个光子出射,且要遵循动量能量守恒,所以背向出射,这样探测器一般只能接收到一个光子。
正电子产生方式:
β + \beta+ β + 电子对效应
在集装箱检测系统中,通常会用 6 MeV 6\text{MeV} 6 MeV 6 MeV 6\text{MeV} 6 MeV 6 MeV 6\text{MeV} 6 MeV
当我们测量某个放射源(例如 137 Cs ^{137}\text{Cs} 137 Cs m m m n n n m m m
因为探测器的 R 0 R_0 R 0 C 0 C_0 C 0 0 0 0
用 NaI(Tl) 探测器测某单能 γ \gamma γ 137 Cs ^{137}\text{Cs} 137 Cs 0.622 MeV 0.622\text{MeV} 0.622 MeV 0.622 MeV 0.622\text{MeV} 0.622 MeV 1.324 MeV 1.324\text{MeV} 1.324 MeV
和峰产生原因:因为在分辨时间里进入探测器中两个伽马光子,在这些时间内,两者能量全部沉积,产生的电压信号会叠在一起,自然就得到了两个全能峰之和的能量。
和峰不可以完全消除,原因如下:
探测器的分辨时间不可能变成 0 0 0
伽马源总可能产生两个几乎在同一时间发射的伽马光子并进入探测器内。
若你拥有活度已知(大小可以“随心所欲”地设定)的放射源,以及本征效率已知、死时间很小(可忽略)的探测器和计数器,是否可以制备出一个比较精准的秒表来?
气体探测器在测量中子和 γ \gamma γ γ \gamma γ
涉及中子探测,暂略
从气体探测器开始,我们会学习 3 种探测器(气体探测器又可以分为:普通电离室、圆柱形电离室、屏栅电离室、正比计数器、G-M 管)。这些探测器都会将射线沉积在灵敏体积内的能量转换为电流。提问:
电流的形状(不是幅度)是确定的吗?对哪些探测器可以认为是确定的,对哪些则不能认为是确定的?
电流的形状若不定,则会对射线能量的分析造成什么影响?我们又是如何解决这个问题的?
如果电流形状不定,就需要考虑弹道亏损,因为形状定的话说明弹道亏损成固定比例。解决这个问题就靠增大 R 0 C 0 R_0C_0 R 0 C 0 τ \tau τ
进入探测器的学习阶段之后,我们就免不了老提“等效电路”这个术语,那么构成等效电路的电阻、电容是哪些呢?这个电路有个冲击响应,可以由什么函数来描述呢?这个冲击响应又为什么会对一个探测器是工作在“脉冲”模式,还是工作在“累计”模式构成影响呢?
冲击响应用指数下降 h ( t ) h(t) h ( t )
V ( t ) = I ( t ) ∗ h ( t ) V(t) = I(t) * h(t) V ( t ) = I ( t ) ∗ h ( t ) h ( t ) h(t) h ( t ) V ( t ) V(t) V ( t ) V ( t ) V(t) V ( t )
在正比计数器中,我们用的 R 0 C 0 R_0C_0 R 0 C 0 μ s \mu\text{s} μ s V V V E dep E_{\text{dep}} E dep
因为正比计数器的电流形状是确定的,故虽然弹道亏损存在,但对于不同的电流信号产生的是相同倍数的变化,之后经过的雪崩过程对信号的增益倍数整体上也是相同的,故电压与能量之间成正比关系。输出脉冲幅度 h ∼ N A e / C 0 h \sim NAe/C_0 h ∼ N A e / C 0
气体探测器的 γ \gamma γ
对 γ \gamma γ 1 − e − N σ D = 1 − e − N A ρ σ A D 1-\mathrm{e}^{-N\sigma D} = 1 - \mathrm{e}^{-N_A \rho \frac{\sigma}{A} D} 1 − e − N σ D = 1 − e − N A ρ A σ D D D D Z Z Z ρ \rho ρ N N N
我们用无机闪烁体可以测量射线的沉积能量,此时一般 R 0 C 0 R_0C_0 R 0 C 0
电流形状是确定的,弹道亏损的程度也是确定的,所以电压与沉积的能量是成正比的。
众所周知,闪烁体探测器的探测效率可以说是最好的,但是它的能量分辨率却排在半导体、气体之后,几乎是最差的,这是为什么?
ν ξ 2 = ν ξ 1 2 + ν ξ 2 2 E ( ξ 1 ) + ⋯ \nu_{\xi}^2 = \nu_{\xi_1}^2 + \frac{\nu_{\xi_2}^2}{E(\xi_1)} + \cdots ν ξ 2 = ν ξ 1 2 + E ( ξ 1 ) ν ξ 2 2 + ⋯
荧光光子在闪烁体中存在自吸收,导致 E ( ξ 1 ) 变小 E(\xi_1) 变小 E ( ξ 1 ) 变小
荧光光子被输运到光阴极的概率不同,同能量不同位置的电离到达光阴极的荧光光子数目不同,导致 ν ξ 2 2 \nu_{\xi_2}^2 ν ξ 2 2
荧光光子在光阴级转换为电子,损失了数目,增加了涨落,光电倍增过程也有统计涨落。
在金硅面垒探测器中,PN 结的作用是巨大的,如果没有 PN 结,半导体探测器能量分辨率好的优点就不可能发挥出来,这其中具体的道理是什么呢?
PN 结显著增大了半导体的电阻率,如果电阻率较小,外加电压会导致显著的暗电流,淹没掉所测的信号;即使消除暗电流,产生的噪声电压也会显著恶化能量分辨率;且欧姆热效应会使半导体发热,会进一步降低电阻率,导致能量分辨率更差。
金硅面垒探测器通常只适合于测量重带电粒子和低能电子,对于高能 γ \gamma γ γ \gamma γ
探测效率:
1 − e − N σ D = 1 − e − N A ρ σ A D 1-\mathrm{e}^{-N\sigma D} = 1 - \mathrm{e}^{-N_A \rho \frac{\sigma}{A} D} 1 − e − N σ D = 1 − e − N A ρ A σ D
耗尽层宽度
W = 2 ε V 0 e N i W = \sqrt{\frac{2\varepsilon V_0}{eN_i}} W = e N i 2 ε V 0
Ge 的 Z Z Z σ \sigma σ
高纯锗探测器杂质密度 N i N_i N i W W W D D D
在半导体探测器中,前置放大器的时间常数 R 0 C 0 R_0C_0 R 0 C 0 ms \text{ms} ms
半导体探测器的电流形状不确定,故需要削减弹道亏损,需要让 R 0 C 0 R_0C_0 R 0 C 0 τ \tau τ
在三种探测器中,等效电路中的 C 0 C_0 C 0 C 1 C_1 C 1 C ′ C' C ′ C i C_i C i C 1 C_1 C 1 C 0 C_0 C 0 C 1 C_1 C 1
PN结型半导体探测器
工作电压 V 0 V_0 V 0 W = 2 ε V 0 e N i W = \sqrt{\frac{2\varepsilon V_0}{eN_i}} W = e N i 2 ε V 0 C 0 ∝ V 0 − 1 2 C_0 \propto V_0^{-\frac12} C 0 ∝ V 0 − 2 1
在第七章的学习中,我们知道了大的数量往往意味着好的统计性(即相对涨落小),但这个结论对于级联变量并不成立,因为级联变量中的第二级过程虽然增加了数量,却实际上恶化了统计性(相对涨落增大)。请你回顾下气体、闪烁和半导体探测器,列举出在这些探测器中的哪些过程涉及到了级联变量?
脉冲探测器:源发射粒子数(泊松)——进入探测器粒子数(泊松)——被探测到粒子数(泊松)
正比计数器:能量沉积转化为电子离子对(法诺)——电子离子对倍增(雪崩);
闪烁探测器:能量沉积转化荧光光子(法诺)——产生光电子——第一打拿极收集——光电倍增(级联)
在一个用来测量核计数的探测器系统中,死时间是否必然存在?为什么?如果用 NaI(Tl)探测器去测量某 γ \gamma γ 10000 cps 10000\text{cps} 10000 cps 0.5 0.5 0.5 10 μ s 10\mu\text{s} 10 μ s 1 / 0.9 1/0.9 1/0.9
死时间必然存在,因为 R 0 C 0 R_0C_0 R 0 C 0
计算错误,错误如下:
没有计算全谱计数率 10000 cps / 0.5 = 20000 cps 10000\text{cps} / 0.5 = 20000\text{cps} 10000 cps /0.5 = 20000 cps
在满足 n τ D ≪ 1 n\tau_D \ll 1 n τ D ≪ 1 f τ = 1 − n τ D f_{\tau} = 1 -n\tau_D f τ = 1 − n τ D
校正因子使用 n / m n/m n / m m / n m/n m / n
真符合发生的条件是什么?偶然符合能被完全消除吗?请分别解释其原因。
辐射测量方法问题,暂略
在 γ \gamma γ
光电峰
康普顿边沿、反散射峰
全能峰、单逃逸峰、双逃逸峰
湮没峰
特征X射线峰(内转换)
和峰
我们用 NaI(Tl)探测器来测量某 γ \gamma γ γ \gamma γ
与源强是有关的:
能谱中大多数峰的高度与计数率成正比,但和峰的增长与其他峰不成正比,因此形状改变;
当源强过低时,部分信号可能被本底淹没;
在测量 γ \gamma γ
单/双逃逸峰:入射粒子能量沉积过程中,探测器内电子对效应产生正电子,其湮没产生的一个/一对湮没光子逃逸。
光电峰:退激过程产生的特征X射线逃逸。
康普顿散射:康普顿效应产生的散射光子逃逸。
在测量能量很低的慢中子时,例如 1 eV 1\text{eV} 1 eV
中子测量问题,暂略
在测量慢中子时,有个中子灵敏度的概念,请问它的量纲是什么?怎么理解它的物理意义?
中子测量问题,暂略
对于数 MeV \text{MeV} MeV
中子测量问题,暂略
在 F.Reines 和 C.L. Cowan 开展的反电子中微子测量实验中,利用反电子中微子和质子产生了正电子和中子,通过正电子事件和中子事件的符合,确认了反电子中微子的存在。在这个过程中,正电子湮没得快,中子最终被 113 Cd ^{113}\text{Cd} 113 Cd 1 MeV 1\text{MeV} 1 MeV 113 Cd ^{113}\text{Cd} 113 Cd
中子测量问题,暂略
入射粒子带来的轨道角动量有不同的组成( s , p , d , f , ⋯ s,p,d,f,\cdots s , p , d , f , ⋯ 轨道角动量 来分析核反应截面。
对于核反应
A + a ⟶ B + b A + a \longrightarrow B + b A + a ⟶ B + b
设入射粒子 a a a v a v_a v a A A A ρ \rho ρ 碰撞参数 ),在质心系下考虑,相对运动动量
p = 2 μ T ′ = μ v a = m A m a + m A m a v a p = \sqrt{2\mu T'} = \mu v_a = \frac{m_A}{m_a+m_A} m_a v_a p = 2 μ T ′ = μ v a = m a + m A m A m a v a
约化德布罗意波长
ˉ λ = ℏ p \mkern5mu\bar{}\mkern-5mu\lambda = \frac{\hbar}{p} ˉ λ = p ℏ
相对运动的角动量
L = p ⋅ ρ = ρ ˉ λ ℏ L = p \cdot \rho = \frac{\rho}{\mkern5mu\bar{}\mkern-5mu\lambda} \hbar L = p ⋅ ρ = ˉ λ ρ ℏ
由于轨道角动量是量子化的,即 L = l ℏ ( l = 0 , 1 , 2 , ⋯ ) L=l\hbar \kern 1em (l=0,1,2,\cdots) L = l ℏ ( l = 0 , 1 , 2 , ⋯ )
ρ ˉ λ = 0 , 1 , 2 , 3 , ⋯ ⟹ ρ = l ˉ λ = 0 ˉ λ , 1 ˉ λ , 2 ˉ λ , ⋯ \frac{\rho}{\mkern5mu\bar{}\mkern-5mu\lambda} = 0,1,2,3,\cdots \Longrightarrow \rho = l \mkern5mu\bar{}\mkern-5mu\lambda = 0\mkern5mu\bar{}\mkern-5mu\lambda, 1\mkern5mu\bar{}\mkern-5mu\lambda, 2\mkern5mu\bar{}\mkern-5mu\lambda, \cdots ˉ λ ρ = 0 , 1 , 2 , 3 , ⋯ ⟹ ρ = l ˉ λ = 0 ˉ λ , 1 ˉ λ , 2 ˉ λ , ⋯
这样,入射粒子 a a a A A A
考虑到核力是短程力,为使碰撞能够发生,碰撞参数应有最大值的限制,即
ρ = l ˉ λ ≤ R = R a + R A \rho = l\mkern5mu\bar{}\mkern-5mu\lambda \le R = R_a + R_A ρ = l ˉ λ ≤ R = R a + R A
则轨道角动量量子数 l l l
l ≤ R ˉ λ = l max l \le \frac{R}{\mkern5mu\bar{}\mkern-5mu\lambda} = l_{\max} l ≤ ˉ λ R = l m a x
轨道角动量为 l ℏ l\hbar l ℏ
S l = π ( ρ l + 1 2 − ρ l 2 ) = π [ ( l + 1 ) 2 − l 2 ] ˉ λ 2 = ( 2 l + 1 ) π ˉ λ 2 S_l = \pi (\rho_{l+1}^2 - \rho_l^2) = \pi [(l+1)^2 - l^2] \mkern5mu\bar{}\mkern-5mu\lambda^2 = (2l+1) \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 S l = π ( ρ l + 1 2 − ρ l 2 ) = π [( l + 1 ) 2 − l 2 ] ˉ λ 2 = ( 2 l + 1 ) π ˉ λ 2
则发生核反应的截面
σ r , l ≤ S l = ( 2 l + 1 ) π ˉ λ 2 \sigma_{r,l} \le S_l = (2l+1) \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 σ r , l ≤ S l = ( 2 l + 1 ) π ˉ λ 2
总截面
σ = ∑ l = 0 R / ˉ λ ( 2 l + 1 ) π ˉ λ 2 = π ( R + ˉ λ ) 2 \sigma = \sum_{l=0}^{R/\mkern5mu\bar{}\mkern-5mu\lambda} (2l+1) \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 = \pi (R + \mkern5mu\bar{}\mkern-5mu\lambda)^2 σ = l = 0 ∑ R / ˉ λ ( 2 l + 1 ) π ˉ λ 2 = π ( R + ˉ λ ) 2
其中 R R R ˉ λ \mkern5mu\bar{}\mkern-5mu\lambda ˉ λ
向 x x x e i k x \mathrm{e}^{\mathrm{i}kx} e i k x
ψ i = e i k x = e i k r cos θ = ∑ l = 0 + ∞ ( 2 l + 1 ) i l ⋅ j l ( k r ) ⋅ P l ( cos θ ) \psi_i = \mathrm{e}^{\mathrm{i}kx} = \mathrm{e}^{\mathrm{i}kr\cos\theta} = \sum_{l=0}^{+\infty} (2l+1)\mathrm{i}^l \cdot j_l(kr) \cdot \mathrm{P}_l(\cos\theta) ψ i = e i k x = e i k r c o s θ = l = 0 ∑ + ∞ ( 2 l + 1 ) i l ⋅ j l ( k r ) ⋅ P l ( cos θ )
其中 j l ( k r ) j_l(kr) j l ( k r ) k r ≫ 1 kr \gg 1 k r ≫ 1
j l ( k r ) ≈ sin ( k r − l π / 2 ) k r = i e − i ( k r − l π / 2 ) − e i ( k r − l π / 2 ) 2 k r j_l(kr) \approx \frac{\sin(kr-l\pi/2)}{kr} = \mathrm{i} \frac{\mathrm{e}^{-\mathrm{i}(kr-l\pi/2)} - \mathrm{e}^{\mathrm{i}(kr-l\pi/2)}}{2kr} j l ( k r ) ≈ k r sin ( k r − l π /2 ) = i 2 k r e − i ( k r − l π /2 ) − e i ( k r − l π /2 )
故
ψ i = 1 2 k r ∑ l = 0 + ∞ ( 2 l + 1 ) i l + 1 [ e − i ( k r − l π 2 ) − e i ( k r − l π 2 ) ] P l ( cos θ ) \psi_i = \frac{1}{2kr} \sum_{l=0}^{+\infty} (2l+1)\mathrm{i}^{l+1} \left[ \mathrm{e}^{-\mathrm{i}(kr-\frac{l\pi}{2})} - \mathrm{e}^{\mathrm{i}(kr-\frac{l\pi}{2})} \right] \mathrm{P}_l(\cos\theta) ψ i = 2 k r 1 l = 0 ∑ + ∞ ( 2 l + 1 ) i l + 1 [ e − i ( k r − 2 l π ) − e i ( k r − 2 l π ) ] P l ( cos θ )
其中 e − i ( k r − l π / 2 ) \mathrm{e}^{-\mathrm{i}(kr-l\pi/2)} e − i ( k r − l π /2 ) r r r 入射球面波 ; e i ( k r − l π / 2 ) \mathrm{e}^{\mathrm{i}(kr-l\pi/2)} e i ( k r − l π /2 ) r r r 出射球面波 。
若原点上有靶核,对入射波没有影响,而散射会导致出射波函数的变化,即 e i ( k r − l π / 2 ) \mathrm{e}^{\mathrm{i}(kr-l\pi/2)} e i ( k r − l π /2 ) η l \eta_l η l
ψ = 1 2 k r ∑ l = 0 + ∞ ( 2 l + 1 ) i l + 1 [ e − i ( k r − l π 2 ) − η l ⋅ e i ( k r − l π 2 ) ] P l ( cos θ ) \psi = \frac{1}{2kr} \sum_{l=0}^{+\infty} (2l+1)\mathrm{i}^{l+1} \left[ \mathrm{e}^{-\mathrm{i}(kr-\frac{l\pi}{2})} - \eta_l \cdot \mathrm{e}^{\mathrm{i}(kr-\frac{l\pi}{2})} \right] \mathrm{P}_l(\cos\theta) ψ = 2 k r 1 l = 0 ∑ + ∞ ( 2 l + 1 ) i l + 1 [ e − i ( k r − 2 l π ) − η l ⋅ e i ( k r − 2 l π ) ] P l ( cos θ )
这里的出射波系数 η l \eta_l η l l l l l l l η l \eta_l η l
散射时 ∣ η l ∣ = 1 |\eta_l| = 1 ∣ η l ∣ = 1
反应时 ∣ η l ∣ < 1 |\eta_l| < 1 ∣ η l ∣ < 1
考虑靶核导致的散射对应的波函数,其应该为有靶核时的波函数与无靶核时的波函数之差,即
ψ s c = ψ − ψ i = 1 2 k r ∑ l = 0 + ∞ ( 2 l + 1 ) i l + 1 [ e i ( k r − l π 2 ) − η l ⋅ e i ( k r − l π 2 ) ] P l ( cos θ ) = 1 2 k r ∑ l = 0 + ∞ ( 2 l + 1 ) i l + 1 ( 1 − η l ) e i ( k r − l π 2 ) P l ( cos θ ) = 1 2 k r ∑ l = 0 + ∞ ( 2 l + 1 ) i l + 1 ( 1 − η l ) e i k r i − l P l ( cos θ ) = 1 2 k r ∑ l = 0 + ∞ i ( 2 l + 1 ) ( 1 − η l ) e i k r P l ( cos θ ) = ∑ l = 0 + ∞ ψ s c , l \psi_{sc} = \psi - \psi_i \ \ \ = \frac{1}{2kr} \sum_{l=0}^{+\infty} (2l+1)\mathrm{i}^{l+1} \left[ \mathrm{e}^{\mathrm{i}(kr-\frac{l\pi}{2})} - \eta_l \cdot \mathrm{e}^{\mathrm{i}(kr-\frac{l\pi}{2})} \right] \mathrm{P}l(\cos\theta) \ \ \ = \frac{1}{2kr} \sum {l=0}^{+\infty} (2l+1)\ \mathrm{i}^{l+1}\ (1-\eta_l)\ \mathrm{e}^{\mathrm{i}(kr-\frac{l\pi}{2})}\ \mathrm{P}l(\cos\theta) \ \ \ = \frac{1}{2kr} \sum {l=0}^{+\infty} (2l+1)\ \mathrm{i}^{l+1}\ (1-\eta_l)\ \mathrm{e}^{\mathrm{i}kr}\ \mathrm{i}^{-l}\ \mathrm{P}l(\cos\theta) \ \ \ = \frac{1}{2kr} \sum {l=0}^{+\infty} \mathrm{i} (2l+1)\ (1-\eta_l)\ \mathrm{e}^{\mathrm{i}kr}\ \mathrm{P}l(\cos\theta) \ \ \ = \sum {l=0}^{+\infty} \psi_{sc,l} ψ sc = ψ − ψ i = 2 k r 1 l = 0 ∑ + ∞ ( 2 l + 1 ) i l + 1 [ e i ( k r − 2 l π ) − η l ⋅ e i ( k r − 2 l π ) ] P l ( cos θ ) = 2 k r 1 l = 0 ∑ + ∞ ( 2 l + 1 ) i l + 1 ( 1 − η l ) e i ( k r − 2 l π ) P l ( cos θ ) = 2 k r 1 l = 0 ∑ + ∞ ( 2 l + 1 ) i l + 1 ( 1 − η l ) e i k r i − l P l ( cos θ ) = 2 k r 1 l = 0 ∑ + ∞ i ( 2 l + 1 ) ( 1 − η l ) e i k r P l ( cos θ ) = l = 0 ∑ + ∞ ψ sc , l
接下来计算入射波函数与散射波函数对应的概率流密度 j = − i ℏ 2 m ( ψ ∗ ∂ ∂ r ψ − ψ ∂ ∂ r ψ ∗ ) j = -\frac{\mathrm{i}\hbar}{2m}(\psi^\frac{\partial}{\partial r}\psi - \psi\frac{\partial}{\partial r}\psi^ ) j = − 2 m i ℏ ( ψ ∗ ∂ r ∂ ψ − ψ ∂ r ∂ ψ ∗ )
j i = − i ℏ 2 m ( ψ i ∗ ∂ ∂ r ψ i − ψ i ∂ ∂ r ψ i ∗ ) = − i ℏ 2 m ( e − i k x ∂ ∂ x e i k x − e i k x ∂ ∂ x e − i k x ) = − i ℏ 2 m ( i k + i k ) = ℏ k m j_i = -\frac{\mathrm{i}\hbar}{2m}(\psi_i^* \frac{\partial}{\partial r} \psi_i - \psi_i \frac{\partial}{\partial r} \psi_i^*) \ \ \ = -\frac{\mathrm{i}\hbar}{2m}( \mathrm{e}^{-\mathrm{i}kx} \frac{\partial}{\partial x} \mathrm{e}^{\mathrm{i}kx} - \mathrm{e}^{\mathrm{i}kx} \frac{\partial}{\partial x} \mathrm{e}^{-\mathrm{i}kx}) \ \ \ = -\frac{\mathrm{i}\hbar}{2m}(\mathrm{i}k + \mathrm{i}k) \ \ \ = \frac{\hbar k}{m} j i = − 2 m i ℏ ( ψ i ∗ ∂ r ∂ ψ i − ψ i ∂ r ∂ ψ i ∗ ) = − 2 m i ℏ ( e − i k x ∂ x ∂ e i k x − e i k x ∂ x ∂ e − i k x ) = − 2 m i ℏ ( i k + i k ) = m ℏ k
j s c = − i ℏ 2 m ( ψ s c ∗ ∂ ∂ r ψ s c − ψ s c ∂ ∂ r ψ s c ∗ ) = − i ℏ 2 m ( ψ s c ∗ ∂ ∂ r ψ s c − 复共轭项 ) = − i ℏ 2 m { ψ s c ∗ ∂ ∂ r [ 1 2 k r ∑ l = 0 + ∞ i ( 2 l + 1 ) ( 1 − η l ) e i k r P l ( cos θ ) ] − 复共轭项 } = − i ℏ 2 m [ ψ s c ∗ ( − 1 r + i k ) ψ s c − 复共轭项 ] = − i ℏ 2 m [ ( − 1 r + i k ) ∣ ψ s c ∣ 2 − 复共轭项 ] = − i ℏ 2 m ( 2 i k ∣ ψ s c ∣ 2 ) = ℏ k m ∣ ψ s c ∣ 2 = ℏ k m ∣ 1 2 k r ∑ l = 0 + ∞ i ( 2 l + 1 ) ( 1 − η l ) e i k r P l ( cos θ ) ∣ 2 = ℏ k m 1 4 k 2 r 2 ∣ ∑ l = 0 + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) ∣ 2 j_{sc} = -\frac{\mathrm{i}\hbar}{2m} \left(\psi_{sc}^* \frac{\partial}{\partial r} \psi_{sc} - \psi_{sc} \frac{\partial}{\partial r} \psi_{sc}^* \right) \ \ \ = -\frac{\mathrm{i}\hbar}{2m} \left( \psi_{sc}^* \frac{\partial}{\partial r} \psi_{sc} - 复共轭项 \right) \ \ \ = -\frac{\mathrm{i}\hbar}{2m} \left{ \psi_{sc}^* \frac{\partial}{\partial r} \left[ \frac{1}{2kr} \sum_{l=0}^{+\infty} \mathrm{i} (2l+1)\ (1-\eta_l)\ \mathrm{e}^{\mathrm{i}kr}\ \mathrm{P}l(\cos\theta) \right] - 复共轭项 \right} \ \ \ = -\frac{\mathrm{i}\hbar}{2m} \left[ \psi {sc}^* \left( -\frac{1}{r} + \mathrm{i}k \right) \psi_{sc} - 复共轭项 \right] \ \ \ = -\frac{\mathrm{i}\hbar}{2m} \left[ \left( -\frac{1}{r} + \mathrm{i}k \right) |\psi_{sc}|^2 - 复共轭项 \right] \ \ \ = -\frac{\mathrm{i}\hbar}{2m} \left( 2\mathrm{i}k |\psi_{sc}|^2 \right) \ \ \ = \frac{\hbar k}{m} |\psi_{sc}|^2 \ \ \ = \frac{\hbar k}{m} \left| \frac{1}{2kr} \sum_{l=0}^{+\infty} \mathrm{i} (2l+1)\ (1-\eta_l)\ \mathrm{e}^{\mathrm{i}kr}\ \mathrm{P}l(\cos\theta) \right|^2 \ \ \ = \frac{\hbar k}{m} \frac{1}{4k^2r^2} \left| \sum {l=0}^{+\infty} (2l+1)(1-\eta_l) \mathrm{P}_l(\cos\theta) \right|^2 j sc = − 2 m i ℏ ( ψ sc ∗ ∂ r ∂ ψ sc − ψ sc ∂ r ∂ ψ sc ∗ ) = − 2 m i ℏ ( ψ sc ∗ ∂ r ∂ ψ sc − 复共轭项 ) = − 2 m i ℏ { ψ sc ∗ ∂ r ∂ [ 2 k r 1 l = 0 ∑ + ∞ i ( 2 l + 1 ) ( 1 − η l ) e i k r P l ( cos θ ) ] − 复共轭项 } = − 2 m i ℏ [ ψ sc ∗ ( − r 1 + i k ) ψ sc − 复共轭项 ] = − 2 m i ℏ [ ( − r 1 + i k ) ∣ ψ sc ∣ 2 − 复共轭项 ] = − 2 m i ℏ ( 2 i k ∣ ψ sc ∣ 2 ) = m ℏ k ∣ ψ sc ∣ 2 = m ℏ k 2 k r 1 l = 0 ∑ + ∞ i ( 2 l + 1 ) ( 1 − η l ) e i k r P l ( cos θ ) 2 = m ℏ k 4 k 2 r 2 1 l = 0 ∑ + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) 2
故散射微分截面
d σ s c d Ω = j s c ⋅ r 2 d Ω j i d Ω = 1 4 k 2 ∣ ∑ l = 0 + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) ∣ 2 = ˉ λ 2 4 ∣ ∑ l = 0 + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) ∣ 2 \frac{\mathrm{d}\sigma_{sc}}{\mathrm{d}\Omega} = \frac{j_{sc} \cdot r^2 \mathrm{d}\Omega}{j_i \mathrm{d}\Omega} = \frac{1}{4k^2} \left| \sum_{l=0}^{+\infty} (2l+1)(1-\eta_l) \mathrm{P}l(\cos\theta) \right|^2 \ \ \ = \frac{\mkern5mu\bar{}\mkern-5mu\lambda^2}{4} \left| \sum {l=0}^{+\infty} (2l+1)(1-\eta_l) \mathrm{P}_l(\cos\theta) \right|^2 d Ω d σ sc = j i d Ω j sc ⋅ r 2 d Ω = 4 k 2 1 l = 0 ∑ + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) 2 = 4 ˉ λ 2 l = 0 ∑ + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) 2
根据勒让德函数的正交归一化公式
∫ 0 π P l ( cos θ ) P l ′ ( cos θ ) sin θ d θ = 2 2 l + 1 δ l l ′ \int_{0}^{\pi} \mathrm{P}l(\cos\theta) \mathrm{P} {l'}(\cos\theta) \sin\theta \mathrm{d}\theta = \frac{2}{2l+1} \delta_{ll'} ∫ 0 π P l ( cos θ ) P l ′ ( cos θ ) sin θ d θ = 2 l + 1 2 δ l l ′
可得散射的总截面为
σ s c = ∫ d σ s c d Ω d Ω = ˉ λ 2 4 ∫ 0 2 π d φ ∫ 0 π ∣ ∑ l = 0 + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) ∣ 2 sin θ d θ = π ˉ λ 2 2 ∑ l , l ′ = 0 + ∞ ( 2 l + 1 ) ∣ 1 − η l ∣ ( 2 l ′ + 1 ) ∣ 1 − η l ′ ∣ ∫ 0 π P l ( cos θ ) P l ′ ( cos θ ) sin θ d θ = π ˉ λ 2 2 ∑ l = 0 + ∞ ( 2 l + 1 ) 2 ∣ 1 − η l ∣ 2 2 2 l + 1 = π ˉ λ 2 ∑ l = 0 + ∞ ( 2 l + 1 ) ∣ 1 − η l ∣ 2 \sigma_{sc} = \int \frac{\mathrm{d}\sigma_{sc}}{\mathrm{d}\Omega} \mathrm{d}\Omega \ \ \ = \frac{\mkern5mu\bar{}\mkern-5mu\lambda^2}{4} \int_{0}^{2\pi} \mathrm{d}\varphi \int_{0}^{\pi} \left| \sum_{l=0}^{+\infty} (2l+1)(1-\eta_l) \mathrm{P}l(\cos\theta) \right|^2 \sin\theta \mathrm{d}\theta \ \ \ = \frac{\pi \mkern5mu\bar{}\mkern-5mu\lambda^2}{2} \sum {l,l'=0}^{+\infty} (2l+1)\ |1-\eta_l|\ (2l'+1)\ |1-\eta_{l'}| \int_{0}^{\pi} \mathrm{P}l(\cos\theta) \mathrm{P} {l'}(\cos\theta) \sin\theta \mathrm{d}\theta \ \ \ = \frac{\pi \mkern5mu\bar{}\mkern-5mu\lambda^2}{2} \sum_{l=0}^{+\infty} (2l+1)^2\ |1-\eta_l|^2 \frac{2}{2l+1} \ \ \ = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \sum_{l=0}^{+\infty} (2l+1)\ |1-\eta_l|^2 σ sc = ∫ d Ω d σ sc d Ω = 4 ˉ λ 2 ∫ 0 2 π d φ ∫ 0 π l = 0 ∑ + ∞ ( 2 l + 1 ) ( 1 − η l ) P l ( cos θ ) 2 sin θ d θ = 2 π ˉ λ 2 l , l ′ = 0 ∑ + ∞ ( 2 l + 1 ) ∣1 − η l ∣ ( 2 l ′ + 1 ) ∣1 − η l ′ ∣ ∫ 0 π P l ( cos θ ) P l ′ ( cos θ ) sin θ d θ = 2 π ˉ λ 2 l = 0 ∑ + ∞ ( 2 l + 1 ) 2 ∣1 − η l ∣ 2 2 l + 1 2 = π ˉ λ 2 l = 0 ∑ + ∞ ( 2 l + 1 ) ∣1 − η l ∣ 2
由于散射时入射粒子与出射粒子均为 a a a b b b a a a ∣ η l ∣ |\eta_l| ∣ η l ∣ η l \eta_l η l
σ r = π ˉ λ 2 ∑ l = 0 + ∞ ( 2 l + 1 ) ( 1 − ∣ η l ∣ ) 2 \sigma_r = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \sum_{l=0}^{+\infty} (2l+1)\ (1-|\eta_l|)^2 σ r = π ˉ λ 2 l = 0 ∑ + ∞ ( 2 l + 1 ) ( 1 − ∣ η l ∣ ) 2
令
ψ ( r ) = u ( r ) r \psi(r) = \frac{u(r)}{r} ψ ( r ) = r u ( r )
则积分
∫ 0 ? ∫ 0 π ∫ 0 2 π ψ ∗ ψ r 2 d r sin θ d θ d φ = ∫ 0 π ∫ 0 2 π sin θ d θ d φ ∫ 0 ? u ∗ u r 2 r 2 d r = 4 π ∫ 0 ? u ∗ u d r \int_{0}^{?} \int_{0}^{\pi} \int_{0}^{2\pi} \psi^* \psi r^2 \mathrm{d}r \sin\theta \mathrm{d}\theta \mathrm{d}\varphi \ \ \ = \int_{0}^{\pi} \int_{0}^{2\pi} \sin\theta \mathrm{d}\theta \mathrm{d}\varphi \int_{0}^{?} \frac{u^*u}{r^2} r^2 \mathrm{d}r \ \ \ = 4\pi \int_{0}^{?} u^*u \mathrm{d}r ∫ 0 ? ∫ 0 π ∫ 0 2 π ψ ∗ ψ r 2 d r sin θ d θ d φ = ∫ 0 π ∫ 0 2 π sin θ d θ d φ ∫ 0 ? r 2 u ∗ u r 2 d r = 4 π ∫ 0 ? u ∗ u d r
对于低能入射粒子, p p p ˉ λ \mkern5mu\bar{}\mkern-5mu\lambda ˉ λ l max l_{\max} l m a x l = 0 l=0 l = 0
ψ o ( r ) = i 2 k r ( e − i k r − η 0 ⋅ e i k r ) \psi_o(r) = \frac{\mathrm{i}}{2kr} \left( \mathrm{e}^{-\mathrm{i}kr} - \eta_0 \cdot \mathrm{e}^{\mathrm{i}kr} \right) ψ o ( r ) = 2 k r i ( e − i k r − η 0 ⋅ e i k r )
故
u o ( r ) = i 2 k ( e − i k r − η 0 ⋅ e i k r ) u_o(r) = \frac{\mathrm{i}}{2k} \left( \mathrm{e}^{-\mathrm{i}kr} - \eta_0 \cdot \mathrm{e}^{\mathrm{i}kr} \right) u o ( r ) = 2 k i ( e − i k r − η 0 ⋅ e i k r )
在核内(即 r < R r<R r < R p p p ˉ λ \mkern5mu\bar{}\mkern-5mu\lambda ˉ λ u i ( r ) u_i(r) u i ( r )
虽然核内外波函数不同,但函数 u ( r ) u(r) u ( r ) r = R r=R r = R
f = r ( ln u ) ′ ∣ r = R = r u i d u i d r ∣ r = R = r u o d u o d r ∣ r = R f = \left. r\left(\ln u\right)' \right|{r=R} = \frac{r}{u_i} \left. \frac{\mathrm{d}u_i}{\mathrm{d}r} \right| {r=R} = \frac{r}{u_o} \left. \frac{\mathrm{d}u_o}{\mathrm{d}r} \right|_{r=R} f = r ( ln u ) ′ r = R = u i r d r d u i r = R = u o r d r d u o r = R
由核外波函数表达式可得
f = r u o d u o d r ∣ r = R = r − i k e − i k r − i k η 0 ⋅ e i k r e − i k r − η 0 ⋅ e i k r ∣ r = R = R − i k e − i k R − i k η 0 ⋅ e i k R e − i k R − η 0 ⋅ e i k R = f R + i f I f = \frac{r}{u_o} \left. \frac{\mathrm{d}u_o}{\mathrm{d}r} \right|{r=R} = \left. r \frac{ -\mathrm{i}k \mathrm{e}^{-\mathrm{i}kr} - \mathrm{i}k\eta_0 \cdot \mathrm{e}^{\mathrm{i}kr} }{ \mathrm{e}^{-\mathrm{i}kr} - \eta_0 \cdot \mathrm{e}^{\mathrm{i}kr} } \right| {r=R} \ \ \ = R \frac{ -\mathrm{i}k \mathrm{e}^{-\mathrm{i}kR} - \mathrm{i}k\eta_0 \cdot \mathrm{e}^{\mathrm{i}kR} }{ \mathrm{e}^{-\mathrm{i}kR} - \eta_0 \cdot \mathrm{e}^{\mathrm{i}kR} } = f_R + \mathrm{i} f_I f = u o r d r d u o r = R = r e − i k r − η 0 ⋅ e i k r − i k e − i k r − i k η 0 ⋅ e i k r r = R = R e − i k R − η 0 ⋅ e i k R − i k e − i k R − i k η 0 ⋅ e i k R = f R + i f I
由此可用 f f f η 0 \eta_0 η 0
f ⋅ ( e − i k R − η 0 ⋅ e i k R ) = − i k R e − i k R − i k R η 0 ⋅ e i k R ⇓ f e − i k R + i k R e − i k R = η 0 ⋅ ( f e i k R − i k R e i k R ) ⇓ η 0 = f + i k R f − i k R e − 2 i k R f \cdot (\mathrm{e}^{-\mathrm{i}kR} - \eta_0 \cdot \mathrm{e}^{\mathrm{i}kR}) = -\mathrm{i}kR \mathrm{e}^{-\mathrm{i}kR} - \mathrm{i}kR\eta_0 \cdot \mathrm{e}^{\mathrm{i}kR} \ \Downarrow \ f \mathrm{e}^{-\mathrm{i}kR} + \mathrm{i}kR \mathrm{e}^{-\mathrm{i}kR} = \eta_0 \cdot ( f\mathrm{e}^{\mathrm{i}kR} - \mathrm{i}kR \mathrm{e}^{\mathrm{i}kR} ) \ \Downarrow \ \eta_0 = \frac{f+\mathrm{i}kR}{f-\mathrm{i}kR} \mathrm{e}^{-2\mathrm{i}kR} f ⋅ ( e − i k R − η 0 ⋅ e i k R ) = − i k R e − i k R − i k R η 0 ⋅ e i k R ⇓ f e − i k R + i k R e − i k R = η 0 ⋅ ( f e i k R − i k R e i k R ) ⇓ η 0 = f − i k R f + i k R e − 2 i k R
若入射粒子与核的作用已知,则核内波函数 u i u_i u i f f f η 0 \eta_0 η 0
σ s c , 0 = π ˉ λ 2 ∣ 1 − η 0 ∣ 2 \sigma_{sc,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 |1-\eta_0|^2 σ sc , 0 = π ˉ λ 2 ∣1 − η 0 ∣ 2
考虑两种极端的情况:
第一种为 u o ( R ) → 0 u_o(R) \to 0 u o ( R ) → 0 d u o d r ( R ) ≠ 0 \frac{\mathrm{d}u_o}{\mathrm{d}r}(R) \ne 0 d r d u o ( R ) = 0 f = R u o ( R ) d u o d r ( R ) → ∞ f = \frac{R}{u_o(R)} \frac{\mathrm{d}u_o}{\mathrm{d}r}(R) \to \infty f = u o ( R ) R d r d u o ( R ) → ∞
这种情况下,由于核内波函数震荡频率远高于核外,为了保证波函数一阶连续可导,在核内的波函数振幅会很小,相当于入射粒子被核排斥而弹出,几乎不可能进入核内。此时
η 0 = lim f → ∞ f + i k R f − i k R e − 2 i k R = e − 2 i k R \eta_0 = \lim_{f\to\infty} \frac{f+\mathrm{i}kR}{f-\mathrm{i}kR} \mathrm{e}^{-2\mathrm{i}kR} = \mathrm{e}^{-2\mathrm{i}kR} η 0 = f → ∞ lim f − i k R f + i k R e − 2 i k R = e − 2 i k R
对应于势(形状)弹性散射截面 :
σ s c , 0 = π ˉ λ 2 ∣ 1 − η 0 ∣ 2 = π ˉ λ 2 ∣ 1 − e − 2 i k R ∣ 2 \sigma_{sc,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 1 - \eta_0 \right|^2 = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 1 - \mathrm{e}^{-2\mathrm{i}kR} \right|^2 σ sc , 0 = π ˉ λ 2 ∣ 1 − η 0 ∣ 2 = π ˉ λ 2 1 − e − 2 i k R 2
对于低能中子, k R ≪ 1 kR \ll 1 k R ≪ 1 ˉ λ k = 1 \mkern5mu\bar{}\mkern-5mu\lambda k = 1 ˉ λk = 1
σ s c , 0 = π ˉ λ 2 ∣ 2 i k R ∣ 2 = 4 π ˉ λ 2 k 2 R 2 = 4 π R 2 \sigma_{sc,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 2\mathrm{i}kR \right|^2 = 4\pi \mkern5mu\bar{}\mkern-5mu\lambda^2 k^2 R^2 = 4\pi R^2 σ sc , 0 = π ˉ λ 2 ∣ 2 i k R ∣ 2 = 4 π ˉ λ 2 k 2 R 2 = 4 π R 2
第二种为 u o ( R ) u_o(R) u o ( R ) d u o d r ( R ) = 0 \frac{\mathrm{d}u_o}{\mathrm{d}r}(R) = 0 d r d u o ( R ) = 0 f = R u o ( R ) d u o d r ( R ) → 0 f = \frac{R}{u_o(R)} \frac{\mathrm{d}u_o}{\mathrm{d}r}(R) \to 0 f = u o ( R ) R d r d u o ( R ) → 0
这种情况下,为了保证波函数一阶连续可导,在核内的波函数振幅会与核外保持一致,相当于入射粒子进入靶核并发生共振。此时
η 0 = lim f → 0 f + i k R f − i k R e − 2 i k R = − e − 2 i k R \eta_0 = \lim_{f\to0} \frac{f+\mathrm{i}kR}{f-\mathrm{i}kR} \mathrm{e}^{-2\mathrm{i}kR} = -\mathrm{e}^{-2\mathrm{i}kR} η 0 = f → 0 lim f − i k R f + i k R e − 2 i k R = − e − 2 i k R
对应于共振(复合核)散射截面 :
σ s c , 0 = π ˉ λ 2 ∣ 1 − η 0 ∣ 2 = π ˉ λ 2 ∣ 1 + e − 2 i k R ∣ 2 \sigma_{sc,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 1 - \eta_0 \right|^2 = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 1 + \mathrm{e}^{-2\mathrm{i}kR} \right|^2 σ sc , 0 = π ˉ λ 2 ∣ 1 − η 0 ∣ 2 = π ˉ λ 2 1 + e − 2 i k R 2
对于低能中子, k R ≪ 1 kR \ll 1 k R ≪ 1
σ s c , 0 = π ˉ λ 2 ∣ 2 ∣ 2 = 4 π ˉ λ 2 \sigma_{sc,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 2 \right|^2 = 4\pi \mkern5mu\bar{}\mkern-5mu\lambda^2 σ sc , 0 = π ˉ λ 2 ∣ 2 ∣ 2 = 4 π ˉ λ 2
考虑一般的情况,应处于上述两种极端情况之间
σ s c , 0 = π ˉ λ 2 ∣ 1 − η 0 ∣ 2 = π ˉ λ 2 ∣ 1 − f + i k R f − i k R e − 2 i k R ∣ 2 = π ˉ λ 2 ∣ e 2 i k R − f + i k R f − i k R ∣ 2 = π ˉ λ 2 ∣ ( e 2 i k R − 1 ) − 2 i k R f − i k R ∣ 2 = π ˉ λ 2 ∣ ( e 2 i k R − 1 ) − 2 i k R f R + i ( f I − k R ) ∣ 2 = π ˉ λ 2 ∣ A p o t + A r e s ∣ 2 \sigma_{sc,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 1 - \eta_0 \right|^2 = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 1 - \frac{f+\mathrm{i}kR}{f-\mathrm{i}kR} \mathrm{e}^{-2\mathrm{i}kR} \right|^2 \ \ \ = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| \mathrm{e}^{2\mathrm{i}kR} - \frac{f+\mathrm{i}kR}{f-\mathrm{i}kR} \right|^2 \ \ \ = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| (\mathrm{e}^{2\mathrm{i}kR} - 1) - \frac{2\mathrm{i}kR}{f-\mathrm{i}kR} \right|^2 \ \ \ = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| (\mathrm{e}^{2\mathrm{i}kR} - 1) - \frac{2\mathrm{i}kR}{ f_R + \mathrm{i}(f_I - kR) } \right|^2 \ \ \ = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| A_{pot} + A_{res} \right|^2 σ sc , 0 = π ˉ λ 2 ∣ 1 − η 0 ∣ 2 = π ˉ λ 2 1 − f − i k R f + i k R e − 2 i k R 2 = π ˉ λ 2 e 2 i k R − f − i k R f + i k R 2 = π ˉ λ 2 ( e 2 i k R − 1 ) − f − i k R 2 i k R 2 = π ˉ λ 2 ( e 2 i k R − 1 ) − f R + i ( f I − k R ) 2 i k R 2 = π ˉ λ 2 ∣ A p o t + A res ∣ 2
其中 A p o t A_{pot} A p o t
A p o t = e 2 i k R − 1 = e i k R ( e i k R − e − i k R ) = 2 i e i k R sin ( k R ) A_{pot} = \mathrm{e}^{2\mathrm{i}kR} - 1 = \mathrm{e}^{\mathrm{i}kR} ( \mathrm{e}^{\mathrm{i}kR} - \mathrm{e}^{-\mathrm{i}kR} ) = 2\mathrm{i}\mathrm{e}^{\mathrm{i}kR} \sin(kR) A p o t = e 2 i k R − 1 = e i k R ( e i k R − e − i k R ) = 2 i e i k R sin ( k R )
对于低能入射粒子, k R ≪ 1 kR \ll 1 k R ≪ 1
σ p o t , 0 = π ˉ λ 2 ∣ 2 i e i k R sin ( k R ) ∣ 2 ≈ 4 π ˉ λ 2 ( k R ) 2 = 4 π R 2 \sigma_{pot,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| 2\mathrm{i}\mathrm{e}^{\mathrm{i}kR} \sin(kR) \right|^2 \approx 4\pi \mkern5mu\bar{}\mkern-5mu\lambda^2 (kR)^2 = 4\pi R^2 σ p o t , 0 = π ˉ λ 2 2 i e i k R sin ( k R ) 2 ≈ 4 π ˉ λ 2 ( k R ) 2 = 4 π R 2
可知当入射粒子能量不大时,势(形状)弹性散射的截面是个常数,与核的大小有关。
A r e s A_{res} A res
A r e s = − 2 i k R f R + i ( f I − k R ) A_{res} = \frac{-2\mathrm{i}kR}{ f_R + \mathrm{i}(f_I - kR) } A res = f R + i ( f I − k R ) − 2 i k R
故势弹性散射截面
σ r e s , 0 = π ˉ λ 2 ∣ − 2 i k R f R + i ( f I − k R ) ∣ 2 = π ˉ λ 2 4 k 2 R 2 f R 2 + ( f I − k R ) 2 ≈ 4 π ˉ λ 2 k 2 R 2 ( d f R d T ′ ) T ′ = E 0 2 ( T ′ − E 0 ) 2 + ( f I − k R ) 2 \sigma_{res,0} = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \left| \frac{-2\mathrm{i}kR}{ f_R + \mathrm{i}(f_I - kR) } \right|^2 \ \ \ = \pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \frac{4k^2R^2}{ f_R^2 + (f_I - kR)^2 } \ \ \ \approx 4\pi \mkern5mu\bar{}\mkern-5mu\lambda^2 \frac{k^2R^2}{ \left( \cfrac{\mathrm{d}f_R}{\mathrm{d}T'} \right)_{T' = E_0}^2 (T' - E_0)^2 + (f_I - kR)^2 } σ res , 0 = π ˉ λ 2 f R + i ( f I − k R ) − 2 i k R 2 = π ˉ λ 2 f R 2 + ( f I − k R ) 2 4 k 2 R 2 ≈ 4 π ˉ λ 2 ( d T ′ d f R ) T ′ = E 0 2 ( T ′ − E 0 ) 2 + ( f I − k R ) 2 k 2 R 2
计数测量值标准偏差 ( N i N_i N i 泊松分布 )
σ = m = N ‾ = N i \sigma = \sqrt{m} = \sqrt{\overline{N}} = \sqrt{N_i} σ = m = N = N i
计数测量值相对标准偏差 ( N i N_i N i 泊松分布 )
ν = σ m = 1 m = 1 N i \nu = \frac{\sigma}{m} = \frac{1}{\sqrt{m}} = \frac{1}{\sqrt{N_i}} ν = m σ = m 1 = N i 1
计数率
n = N t n = \frac{N}{t} n = t N
其标准偏差
σ n = n t \sigma_n = \sqrt{\frac{n}{t}} σ n = t n
其相对标准偏差
ν n = σ n n = 1 n t = 1 N \nu_n = \frac{\sigma_n}{n} = \frac{1}{\sqrt{nt}} = \frac{1}{\sqrt{N}} ν n = n σ n = n t 1 = N 1
净计数率 ( n s n_{\text{s}} n s t s t_{\text{s}} t s n b n_{\text{b}} n b t b t_{\text{b}} t b
n 0 = n s − n b = N s t s − N b t b n_0 = n_{\text{s}} - n_{\text{b}} = \frac{N_{\text{s}}}{t_{\text{s}}} - \frac{N_{\text{b}}}{t_{\text{b}}} n 0 = n s − n b = t s N s − t b N b
其标准偏差
σ n 0 = n s t s + n b t b \sigma_{n_0} = \sqrt{ \frac{n_{\text{s}}}{t_{\text{s}}} + \frac{n_{\text{b}}}{t_{\text{b}}} } σ n 0 = t s n s + t b n b
其相对标准偏差
ν n 0 = 1 n s − n b n s t s + n b t b \nu_{n_0} = \frac{1}{n_{\text{s}} - n_{\text{b}}} \sqrt{ \frac{n_{\text{s}}}{t_{\text{s}}} + \frac{n_{\text{b}}}{t_{\text{b}}} } ν n 0 = n s − n b 1 t s n s + t b n b
在规定的总测量时间 T = t s + t b T = t_{\text{s}} + t_{\text{b}} T = t s + t b 最佳测量条件 (时间分配 ) 为
t s t b = n s n b t s = n s / n b 1 + n s / n b T , t b = 1 1 + n s / n b T \frac{t_{\text{s}}}{t_{\text{b}}} = \sqrt{\frac{n_{\text{s}}}{n_{\text{b}}}} \ \ \ t_{\text{s}} = \frac{\sqrt{n_{\text{s}}/n_{\text{b}}}}{1+\sqrt{n_{\text{s}}/n_{\text{b}}}}T ,\kern 1em t_{\text{b}} = \frac{1}{1+\sqrt{n_{\text{s}}/n_{\text{b}}}}T t b t s = n b n s t s = 1 + n s / n b n s / n b T , t b = 1 + n s / n b 1 T
在最佳测量条件下得到的测量结果——净计数率的相对方差( T T T
ν n 0 2 = [ 1 n s − n b n s t s + n b t b ] 2 = 1 T n b ( n s / n b − 1 ) 2 = 1 T ( n s − n b ) 2 \nu_{n_0}^2 = \left[ \frac{1}{n_{\text{s}} - n_{\text{b}}} \sqrt{ \frac{n_{\text{s}}}{t_{\text{s}}} + \frac{n_{\text{b}}}{t_{\text{b}}} } \right]^2 = \frac{1}{Tn_{\text{b}}(\sqrt{n_{\text{s}}/n_{\text{b}}}-1)^2} = \frac{1}{T(\sqrt{n_{\text{s}}}-\sqrt{n_{\text{b}}})^2} ν n 0 2 = [ n s − n b 1 t s n s + t b n b ] 2 = T n b ( n s / n b − 1 ) 2 1 = T ( n s − n b ) 2 1
在 ν n 0 \nu_{n_0} ν n 0
T min = 1 n b ν n 0 2 ( n s / n b − 1 ) 2 = 1 ν n 0 2 ( n s − n b ) 2 T_{\min} = \frac{1}{n_{\text{b}}\nu_{n_0}^2(\sqrt{n_{\text{s}}/n_{\text{b}}}-1)^2} = \frac{1}{\nu_{n_0}^2(\sqrt{n_{\text{s}}}-\sqrt{n_{\text{b}}})^2} T m i n = n b ν n 0 2 ( n s / n b − 1 ) 2 1 = ν n 0 2 ( n s − n b ) 2 1
电离室 ( F F F
η = 2.355 F N ‾ = 2.355 F W E \eta = 2.355 \sqrt{\frac{F}{,\overline{N},}} = 2.355 \sqrt{\frac{FW}{E}} η = 2.355 N F = 2.355 E F W
正比计数器 ( ν A 2 = 0.68 \nu_A^2 = 0.68 ν A 2 = 0.68
η = 2.355 F + 0.68 N ‾ \eta = 2.355 \sqrt{\frac{F+0.68}{\overline{N}}} η = 2.355 N F + 0.68
闪烁探测器 ( n e = E Y ph T n_e = E Y_{\text{ph}} T n e = E Y ph T
η = 2.355 1 n ‾ e [ 1 + δ δ 1 ( 1 δ − 1 ) ] \eta = 2.355 \sqrt{\frac{1}{\overline{n}_e} \left[ 1 + \frac{\delta}{\delta_1} \left( \frac{1}{\delta-1} \right) \right] } η = 2.355 n e 1 [ 1 + δ 1 δ ( δ − 1 1 ) ]
半导体探测器
η = 2.355 F N ‾ = 2.355 F W E \eta = 2.355 \sqrt{\frac{F}{,\overline{N},}} = 2.355 \sqrt{\frac{FW}{E}} η = 2.355 N F = 2.355 E F W
能量分辨率 的两种表示(以电离室或半导体探测器为例,只考虑统计涨落)
η = FWHM E = 2.355 F W E × 100 % \eta = \frac{\text{FWHM}}{E} = 2.355 \sqrt{\frac{FW}{E}} \times 100% η = E FWHM = 2.355 E F W × 100%
用半高宽 (线宽)表示(一般 W W W eV \text{eV} eV E E E MeV \text{MeV} MeV Δ E \Delta E Δ E keV \text{keV} keV
Δ E = FWHM = 2.355 F ⋅ W ⋅ E \Delta E = \text{FWHM} = 2.355 \sqrt{F \cdot W \cdot E} Δ E = FWHM = 2.355 F ⋅ W ⋅ E
当考虑影响分辨率的各种影响因素时,谱仪总分辨率 为
Δ E = FWHM = ∑ i Δ E i 2 \Delta E = \text{FWHM} = \sqrt{ \sum_{i} \Delta E_i^2 } Δ E = FWHM = i ∑ Δ E i 2
电荷灵敏前置放大器的噪声
Δ E noise = Δ E 零电容 + Δ E 电容噪声 = Δ E 零电容 + 噪声斜率 × 探测器电容 \Delta E_{\text{noise}} = \Delta E_{\text{零电容}} + \Delta E_{\text{电容噪声}} = \Delta E_{\text{零电容}} + \text{噪声斜率} \times \text{探测器电容} Δ E noise = Δ E 零电容 + Δ E 电容噪声 = Δ E 零电容 + 噪声斜率 × 探测器电容
或
Δ E noise = 2.355 ⋅ W ⋅ ENC \Delta E_{\text{noise}} = 2.355 \cdot W \cdot \text{ENC} Δ E noise = 2.355 ⋅ W ⋅ ENC
放大器的信噪比 ( h 1 h_1 h 1 σ h 2 \sigma_{h_2} σ h 2
J = h ‾ 1 σ h 2 J = \frac{\overline{h}1}{\sigma {h_2}} J = σ h 2 h 1
放大器噪声对能量分辨率的影响(以电离室为例)
η = 2.355 F N ‾ + 1 J 2 × 100 % \eta = 2.355 \sqrt{\frac{F}{,\overline{N},} + \frac{1}{J^2}} \times 100% η = 2.355 N F + J 2 1 × 100%
准确度 (accuracy):
测量值与被测对象真值的一致程度。
由测量值的平均值与真值的差来描述。
精密度 (precision):
测量的可重复性或可靠性。
可用测量的均方偏差来描述。
数学期望
E ( ξ ) = ∑ i = 1 N 或 ∞ x i ⋅ f ( x i ) E ( X ) = ∫ − ∞ + ∞ x ⋅ f ( x ) d x E(\xi) = \sum_{i=1}^{N\text{或}\infty} x_i \cdot f(x_i) \ \ \ E(X) = \int_{-\infty}^{+\infty} x \cdot f(x)\ \mathrm{d}x E ( ξ ) = i = 1 ∑ N 或 ∞ x i ⋅ f ( x i ) E ( X ) = ∫ − ∞ + ∞ x ⋅ f ( x ) d x
均方偏差 ,简称为方差
D ( ξ ) = ∑ i = 1 N 或 ∞ [ x i − E ( ξ ) ] 2 ⋅ f ( x i ) D ( X ) = ∫ − ∞ + ∞ [ x − E ( X ) ] 2 ⋅ f ( x ) d x D(\xi) = \sum_{i=1}^{N\text{或}\infty} [x_i - E(\xi)]^2 \cdot f(x_i) \ \ \ D(X) = \int_{-\infty}^{+\infty} [x - E(X)]^2 \cdot f(x)\ \mathrm{d}x D ( ξ ) = i = 1 ∑ N 或 ∞ [ x i − E ( ξ ) ] 2 ⋅ f ( x i ) D ( X ) = ∫ − ∞ + ∞ [ x − E ( X ) ] 2 ⋅ f ( x ) d x
均方根偏差
σ = D \sigma = \sqrt{D} σ = D
相对均方偏差
ν 2 = D E 2 \nu^2 = \frac{D}{E^2} ν 2 = E 2 D
相对均方根偏差
ν = σ E \nu = \frac{\sigma}{E} ν = E σ
若 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x 1 , x 2 , ⋯ , x n σ x 1 , σ x 2 , ⋯ , σ x n \sigma_{x_1},\sigma_{x_2},\cdots,\sigma_{x_n} σ x 1 , σ x 2 , ⋯ , σ x n y = f ( x 1 , x 2 , ⋯ , x n ) y=f(x_1,x_2,\cdots,x_n) y = f ( x 1 , x 2 , ⋯ , x n )
σ y 2 = ( ∂ y ∂ x 1 ) 2 σ x 1 2 + ( ∂ y ∂ x 2 ) 2 σ x 2 2 + ⋯ + ( ∂ y ∂ x n ) 2 σ x n 2 \sigma_{y}^2 = \left( \frac{\partial y}{\partial x_1} \right)^2 \sigma_{x_1}^2 + \left( \frac{\partial y}{\partial x_2} \right)^2 \sigma_{x_2}^2 + \cdots + \left( \frac{\partial y}{\partial x_n} \right)^2 \sigma_{x_n}^2 σ y 2 = ( ∂ x 1 ∂ y ) 2 σ x 1 2 + ( ∂ x 2 ∂ y ) 2 σ x 2 2 + ⋯ + ( ∂ x n ∂ y ) 2 σ x n 2
几个简单函数的标准偏差及相对标准偏差如表所示:
函数 f f f 标准偏差 相对标准偏差
y = a x 1 ± b x 2 y = ax_1 \pm bx_2 y = a x 1 ± b x 2 [ ( a σ x 1 ) 2 + ( b σ x 2 ) 2 ] 1 2 [(a\sigma_{x_1})^2 + (b\sigma_{x_2})^2]^{\frac12} [( a σ x 1 ) 2 + ( b σ x 2 ) 2 ] 2 1 [ ( a σ x 1 ) 2 + ( b σ x 2 ) 2 ] 1 2 / ( a x 1 ± b x 2 ) [(a\sigma_{x_1})^2 + (b\sigma_{x_2})^2]^{\frac12}/(ax_1 \pm bx_2) [( a σ x 1 ) 2 + ( b σ x 2 ) 2 ] 2 1 / ( a x 1 ± b x 2 ) y = x 1 ⋅ x 2 y = x_1 \cdot x_2 y = x 1 ⋅ x 2 x 1 ⋅ x 2 [ ( σ x 1 x 1 ) 2 + ( σ x 2 x 2 ) 2 ] 1 2 x_1 \cdot x_2 \left[ \left( \frac{\sigma_{x_1}}{x_1} \right)^2 + \left( \frac{\sigma_{x_2}}{x_2} \right)^2 \right]^{\frac12} x 1 ⋅ x 2 [ ( x 1 σ x 1 ) 2 + ( x 2 σ x 2 ) 2 ] 2 1 [ ( σ x 1 x 1 ) 2 + ( σ x 2 x 2 ) 2 ] 1 2 \left[ \left( \frac{\sigma_{x_1}}{x_1} \right)^2 + \left( \frac{\sigma_{x_2}}{x_2} \right)^2 \right]^{\frac12} [ ( x 1 σ x 1 ) 2 + ( x 2 σ x 2 ) 2 ] 2 1 y = x 1 / x 2 y = x_1 / x_2 y = x 1 / x 2 x 1 x 2 [ ( σ x 1 x 1 ) 2 + ( σ x 2 x 2 ) 2 ] 1 2 \frac{x_1}{x_2}\left[ \left( \frac{\sigma_{x_1}}{x_1} \right)^2 + \left( \frac{\sigma_{x_2}}{x_2} \right)^2 \right]^{\frac12} x 2 x 1 [ ( x 1 σ x 1 ) 2 + ( x 2 σ x 2 ) 2 ] 2 1 [ ( σ x 1 x 1 ) 2 + ( σ x 2 x 2 ) 2 ] 1 2 \left[ \left( \frac{\sigma_{x_1}}{x_1} \right)^2 + \left( \frac{\sigma_{x_2}}{x_2} \right)^2 \right]^{\frac12} [ ( x 1 σ x 1 ) 2 + ( x 2 σ x 2 ) 2 ] 2 1
E ( C ⋅ ξ ) = C ⋅ E ( ξ ) D ( C ⋅ ξ ) = C 2 ⋅ D ( ξ ) ν 2 ( C ⋅ ξ ) = D ( ξ ) [ E ( ξ ) ] 2 E(C \cdot \xi) = C \cdot E(\xi) \ \ \ D(C \cdot \xi) = C^2 \cdot D(\xi) \ \ \ \nu^2(C \cdot \xi) = \frac{D(\xi)}{[E(\xi)]^2} E ( C ⋅ ξ ) = C ⋅ E ( ξ ) D ( C ⋅ ξ ) = C 2 ⋅ D ( ξ ) ν 2 ( C ⋅ ξ ) = [ E ( ξ ) ] 2 D ( ξ )
E ( ξ 1 ± ξ 2 ± ⋯ ± ξ n ) = E ( ξ 1 ) ± E ( ξ 2 ) ± ⋯ ± E ( ξ n ) D ( ξ 1 ± ξ 2 ± ⋯ ± ξ n ) = D ( ξ 1 ) + D ( ξ 2 ) + ⋯ + D ( ξ n ) E(\xi_1 \pm \xi_2 \pm \cdots \pm \xi_n) = E(\xi_1) \pm E(\xi_2) \pm \cdots \pm E(\xi_n) \ \ \ D(\xi_1 \pm \xi_2 \pm \cdots \pm \xi_n) = D(\xi_1) + D(\xi_2) + \cdots + D(\xi_n) E ( ξ 1 ± ξ 2 ± ⋯ ± ξ n ) = E ( ξ 1 ) ± E ( ξ 2 ) ± ⋯ ± E ( ξ n ) D ( ξ 1 ± ξ 2 ± ⋯ ± ξ n ) = D ( ξ 1 ) + D ( ξ 2 ) + ⋯ + D ( ξ n )
E ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) ⋯ E ( ξ n ) D ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) = ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) 2 [ ( D ( ξ 1 ) ξ 1 2 ) 2 + ( D ( ξ 1 ) ξ 1 2 ) 2 + ⋯ + ( D ( ξ 1 ) ξ 1 2 ) 2 ] ν 2 ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) = ν 2 ( ξ 1 ) + ν 2 ( ξ 2 ) + ⋯ + ν 2 ( ξ n ) E(\xi_1 \cdot \xi_2 \cdots \xi_n) = E(\xi_1) \cdot E(\xi_2) \cdots E(\xi_n) \ \ \ D(\xi_1 \cdot \xi_2 \cdots \xi_n) = (\xi_1 \cdot \xi_2 \cdots \xi_n)^2 \left[ \left(\frac{D(\xi_1)}{\xi_1^2}\right)^2 + \left(\frac{D(\xi_1)}{\xi_1^2}\right)^2 + \cdots + \left(\frac{D(\xi_1)}{\xi_1^2}\right)^2 \right] \ \ \ \nu^2(\xi_1 \cdot \xi_2 \cdots \xi_n) = \nu^2(\xi_1) + \nu^2(\xi_2) + \cdots + \nu^2(\xi_n) E ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) ⋯ E ( ξ n ) D ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) = ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) 2 [ ( ξ 1 2 D ( ξ 1 ) ) 2 + ( ξ 1 2 D ( ξ 1 ) ) 2 + ⋯ + ( ξ 1 2 D ( ξ 1 ) ) 2 ] ν 2 ( ξ 1 ⋅ ξ 2 ⋯ ξ n ) = ν 2 ( ξ 1 ) + ν 2 ( ξ 2 ) + ⋯ + ν 2 ( ξ n )
E ( ξ ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) D ( ξ ) = [ E ( ξ 2 ) ] 2 ⋅ D ( ξ 1 ) + E ( ξ 1 ) ⋅ D ( ξ 2 ) ν ξ 2 = D ( ξ ) [ E ( ξ ) ] 2 = ν ξ 1 2 + 1 E ( ξ 1 ) ν ξ 2 2 E(\xi) = E(\xi_1) \cdot E(\xi_2) \ \ \ D(\xi) = [E(\xi_2)]^2 \cdot D(\xi_1) + E(\xi_1) \cdot D(\xi_2) \ \ \ \nu_\xi^2 = \frac{D(\xi)}{[E(\xi)]^2} = \nu_{\xi_1}^2 + \frac{1}{E(\xi_1)} \nu_{\xi_2}^2 E ( ξ ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) D ( ξ ) = [ E ( ξ 2 ) ] 2 ⋅ D ( ξ 1 ) + E ( ξ 1 ) ⋅ D ( ξ 2 ) ν ξ 2 = [ E ( ξ ) ] 2 D ( ξ ) = ν ξ 1 2 + E ( ξ 1 ) 1 ν ξ 2 2
若第一级随机变量的数学期望很大,则可忽略第二级随机变量的相对方差对串级随机变量的相对方差的贡献。
E ( ξ ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) ⋯ E ( ξ N ) ν ξ 2 = ν ξ 1 2 + ν ξ 2 2 E ( ξ 1 ) + ν ξ 3 2 E ( ξ 1 ) ⋅ E ( ξ 2 ) + ⋯ + ν ξ N 2 E ( ξ 1 ) ⋅ E ( ξ 2 ) ⋯ E ( ξ N − 1 ) E(\xi) = E(\xi_1) \cdot E(\xi_2) \cdots E(\xi_N) \ \ \ \nu_\xi^2 = \nu_{\xi_1}^2 + \frac{\nu_{\xi_2}^2}{E(\xi_1)} + \frac{\nu_{\xi_3}^2}{E(\xi_1) \cdot E(\xi_2)} + \cdots + \frac{\nu_{\xi_N}^2}{E(\xi_1) \cdot E(\xi_2) \cdots E(\xi_{N-1})} E ( ξ ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) ⋯ E ( ξ N ) ν ξ 2 = ν ξ 1 2 + E ( ξ 1 ) ν ξ 2 2 + E ( ξ 1 ) ⋅ E ( ξ 2 ) ν ξ 3 2 + ⋯ + E ( ξ 1 ) ⋅ E ( ξ 2 ) ⋯ E ( ξ N − 1 ) ν ξ N 2
对计数率进行 k k k t i t_i t i N i N_i N i n i n_i n i 加权平均值
n ‾ = ∑ i t i n i ∑ i t i = ∑ i N i ∑ i t i \overline{n} = \frac{\sum_i t_i n_i}{\sum_i t_i} = \frac{\sum_i N_i}{\sum_i t_i} n = ∑ i t i ∑ i t i n i = ∑ i t i ∑ i N i
标准偏差
σ n ‾ = ∑ i σ N i 2 ∑ i t i = ∑ i N i ∑ i t i = n ‾ ∑ i t i \sigma_{\overline{n}} = \frac{\sqrt{\sum_i \sigma_{N_i}^2}}{\sum_i t_i} = \frac{\sqrt{\sum_i N_i}}{\sum_i t_i} = \sqrt{\frac{\overline{n}}{\sum_i t_i}} σ n = ∑ i t i ∑ i σ N i 2 = ∑ i t i ∑ i N i = ∑ i t i n
相对标准偏差
ν n ‾ = σ n ‾ n ‾ = 1 ∑ i N i \nu_{\overline{n}} = \frac{\sigma_{\overline{n}}}{\overline{n}} = \sqrt{\frac{1}{\sum_i N_i}} ν n = n σ n = ∑ i N i 1
就统计误差而言,无论是一次测量还是多次测量,只要总的计数相同 ,多次测量平均计数率的相对误差和一次测量的计数率的相对误差是一致的。
核衰变在任何情况下严格服从二项式分布:
p = 1 − e − λ t p = 1 - \mathrm{e}^{-\lambda t} p = 1 − e − λ t
当 λ t \lambda t λ t
m = σ 2 = N 0 ⋅ λ ⋅ t m = \sigma^2 = N_0 \cdot \lambda \cdot t m = σ 2 = N 0 ⋅ λ ⋅ t
当 m > 20 m>20 m > 20
伯努利 串级伯努利 仍为伯努利 :
p = p 1 ⋅ p 2 E ( ξ ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) ν ξ 2 = 1 − p 1 p 1 + 1 p 1 1 − p 2 p 2 = 1 − p 1 p 2 p 1 p 2 p = p_1 \cdot p_2 \ \ \ E(\xi) = E(\xi_1) \cdot E(\xi_2) \ \ \ \nu_\xi^2 = \frac{1-p_1}{p_1} + \frac{1}{p_1} \frac{1-p_2}{p_2} = \frac{1-p_1p_2}{p_1p_2} p = p 1 ⋅ p 2 E ( ξ ) = E ( ξ 1 ) ⋅ E ( ξ 2 ) ν ξ 2 = p 1 1 − p 1 + p 1 1 p 2 1 − p 2 = p 1 p 2 1 − p 1 p 2
泊松 串级伯努利 仍为泊松 :
E ( ξ ) = m 1 ⋅ p 2 ν ξ 2 = 1 m 1 + 1 m 1 1 − p 2 p 2 = 1 m 1 p 2 E(\xi) = m_1 \cdot p_2 \ \ \ \nu_\xi^2 = \frac{1}{m_1} + \frac{1}{m_1} \frac{1-p_2}{p_2} = \frac{1}{m_1p_2} E ( ξ ) = m 1 ⋅ p 2 ν ξ 2 = m 1 1 + m 1 1 p 2 1 − p 2 = m 1 p 2 1
相互独立的服从泊松分布的随机变量之和 服从泊松分布:
E ( ξ 1 + ξ 2 ) = E ( ξ 1 ) + E ( ξ 2 ) D ( ξ 1 + ξ 2 ) = D ( ξ 1 ) + D ( ξ 2 ) E(\xi_1 + \xi_2) = E(\xi_1) + E(\xi_2) \ \ \ D(\xi_1 + \xi_2) = D(\xi_1) + D(\xi_2) E ( ξ 1 + ξ 2 ) = E ( ξ 1 ) + E ( ξ 2 ) D ( ξ 1 + ξ 2 ) = D ( ξ 1 ) + D ( ξ 2 )
由于带电粒子在气体中总的碰撞次数是不确定的,且碰撞过程是不独立的,故带电粒子在气体中电离产生的总电子离子对数不能简单用泊松分布描述,而应使用法诺分布 ,法诺因子
F = σ 2 n ‾ F = \frac{\sigma^2}{\overline{n}} F = n σ 2
气体的法诺因子一般在 1 3 ∼ 1 2 \frac13 \sim \frac12 3 1 ∼ 2 1 0.1 ∼ 0.15 0.1 \sim 0.15 0.1 ∼ 0.15
σ 2 = F ⋅ n ‾ = F ⋅ E W ν 2 = F n ‾ = F ⋅ W E \sigma^2 = F \cdot \overline{n} = F \cdot \frac{E}{W} \ \ \ \nu^2 = \frac{F}{\overline{n}} = \frac{F \cdot W}{E} σ 2 = F ⋅ n = F ⋅ W E ν 2 = n F = E F ⋅ W
第一次,在时间 t b t_{\text{b}} t b 本底 的计数为 N b N_{\text{b}} N b n b = N b / t b n_{\text{b}} = N_{\text{b}} / t_{\text{b}} n b = N b / t b t s t_{\text{s}} t s 样品和本底 的计数为 N s N_{\text{s}} N s n s = N s / t s n_{\text{s}} = N_{\text{s}} / t_{\text{s}} n s = N s / t s 净计数率
n 0 = n s − n b = N s t s − N b t b n_0 = n_{\text{s}} - n_{\text{b}} = \frac{N_{\text{s}}}{t_{\text{s}}} - \frac{N_{\text{b}}}{t_{\text{b}}} n 0 = n s − n b = t s N s − t b N b
其标准偏差 为
σ n 0 = n s t s + n b t b \sigma_{n_0} = \sqrt{ \frac{n_{\text{s}}}{t_{\text{s}}} + \frac{n_{\text{b}}}{t_{\text{b}}} } σ n 0 = t s n s + t b n b
其相对标准偏差 为
ν n 0 = 1 n s − n b n s t s + n b t b \nu_{n_0} = \frac{1}{n_{\text{s}} - n_{\text{b}}} \sqrt{ \frac{n_{\text{s}}}{t_{\text{s}}} + \frac{n_{\text{b}}}{t_{\text{b}}} } ν n 0 = n s − n b 1 t s n s + t b n b
在规定的总测量时间 T = t s + t b T = t_{\text{s}} + t_{\text{b}} T = t s + t b 最佳测量条件 (时间分配 ) 为
t s t b = n s n b t s = n s / n b 1 + n s / n b T , t b = 1 1 + n s / n b T \frac{t_{\text{s}}}{t_{\text{b}}} = \sqrt{\frac{n_{\text{s}}}{n_{\text{b}}}} \ \ \ t_{\text{s}} = \frac{\sqrt{n_{\text{s}}/n_{\text{b}}}}{1+\sqrt{n_{\text{s}}/n_{\text{b}}}}T ,\kern 1em t_{\text{b}} = \frac{1}{1+\sqrt{n_{\text{s}}/n_{\text{b}}}}T t b t s = n b n s t s = 1 + n s / n b n s / n b T , t b = 1 + n s / n b 1 T
在最佳测量条件下得到的测量结果——净计数率的相对方差( T T T
ν n 0 2 = [ 1 n s − n b n s t s + n b t b ] 2 = 1 T n b ( n s / n b − 1 ) 2 = 1 T ( n s − n b ) 2 \nu_{n_0}^2 = \left[ \frac{1}{n_{\text{s}} - n_{\text{b}}} \sqrt{ \frac{n_{\text{s}}}{t_{\text{s}}} + \frac{n_{\text{b}}}{t_{\text{b}}} } \right]^2 = \frac{1}{Tn_{\text{b}}(\sqrt{n_{\text{s}}/n_{\text{b}}}-1)^2} = \frac{1}{T(\sqrt{n_{\text{s}}}-\sqrt{n_{\text{b}}})^2} ν n 0 2 = [ n s − n b 1 t s n s + t b n b ] 2 = T n b ( n s / n b − 1 ) 2 1 = T ( n s − n b ) 2 1
在 ν n 0 \nu_{n_0} ν n 0
T min = 1 n b ν n 0 2 ( n s / n b − 1 ) 2 = 1 ν n 0 2 ( n s − n b ) 2 T_{\min} = \frac{1}{n_{\text{b}}\nu_{n_0}^2(\sqrt{n_{\text{s}}/n_{\text{b}}}-1)^2} = \frac{1}{\nu_{n_0}^2(\sqrt{n_{\text{s}}}-\sqrt{n_{\text{b}}})^2} T m i n = n b ν n 0 2 ( n s / n b − 1 ) 2 1 = ν n 0 2 ( n s − n b ) 2 1
若 n b ≫ n 0 n_{\text{b}} \gg n_0 n b ≫ n 0
T min → 4 n b ν n 0 2 n 0 2 T_{\min} \to \frac{4n_{\text{b}}}{\nu_{n_0}^2n_0^2} T m i n → ν n 0 2 n 0 2 4 n b
这表明降低本底可以实现节省测量时间的作用。
相邻脉冲信号时间间隔为 t t t
f ( t ) = m ⋅ e − m ⋅ t f(t) = m \cdot \mathrm{e}^{-m \cdot t} f ( t ) = m ⋅ e − m ⋅ t
其中 m m m
相邻脉冲信号时间间隔的平均值、方差及相对均方根偏差分别为
t ‾ = ∫ 0 + ∞ t ⋅ f ( t ) d t = 1 m σ t 2 = ∫ 0 + ∞ ( t − t ‾ ) 2 ⋅ f ( t ) d t = 1 m 2 ν t = σ t t ‾ = 1 \overline{t} = \int_0^{+\infty} t \cdot f(t)\ \mathrm{d}t = \frac{1}{m} \ \ \ \sigma_t^2 = \int_0^{+\infty} (t-\overline{t})^2 \cdot f(t)\ \mathrm{d}t = \frac{1}{m^2} \ \ \ \nu_t = \frac{\sigma_t}{\overline{t}} = 1 t = ∫ 0 + ∞ t ⋅ f ( t ) d t = m 1 σ t 2 = ∫ 0 + ∞ ( t − t ) 2 ⋅ f ( t ) d t = m 2 1 ν t = t σ t = 1
在计数率较高时,需要使用具有进位系数 S S S S S S t t t
f S ( t ) = ( m t ) S − 1 ( S − 1 ) ! m e − m t f_S(t) = \frac{(mt)^{S-1}}{(S-1)!} m \mathrm{e}^{-mt} f S ( t ) = ( S − 1 )! ( m t ) S − 1 m e − m t
使得 f ( t ) f(t) f ( t ) t S t_S t S
t S = S − 1 m t_S = \frac{S-1}{m} t S = m S − 1
相邻进位脉冲时间间隔的平均值、均方根偏差及相对均方根偏差分别为
T ‾ S = S m σ T S 2 = S m 2 ν T S = 1 S \overline{T}S = \frac{S}{m} \ \ \ \sigma {T_S}^2 = \frac{S}{m^2} \ \ \ \nu_{T_S} = \frac{1}{\sqrt{S}} T S = m S σ T S 2 = m 2 S ν T S = S 1
定义能量分辨率 为
η = Δ E E × 100 % = Δ h h × 100 % \eta = \frac{\Delta E}{E} \times 100% = \frac{\Delta h}{h} \times 100% η = E Δ E × 100% = h Δ h × 100%
式中 Δ E \Delta E Δ E 能谱半高宽 ,即谱峰极大值一半处的全宽度,缩写符号为 FWHM \text{FWHM} FWHM
( Δ E ) 2 = FWHM total 2 = ∑ i ( Δ E i ) 2 = ∑ i FWHM i 2 = FWHM statistical 2 + FWHM drift 2 + FWHM noise 2 + ⋯ (\Delta E)^2 = \text{FWHM}{\text{total}}^2 = \sum {i} (\Delta E_i)^2 = \sum_{i} \text{FWHM}i^2 \ \ \ = \text{FWHM} {\text{statistical}}^2 + \text{FWHM}{\text{drift}}^2 + \text{FWHM} {\text{noise}}^2 + \cdots ( Δ E ) 2 = FWHM total 2 = i ∑ ( Δ E i ) 2 = i ∑ FWHM i 2 = FWHM statistical 2 + FWHM drift 2 + FWHM noise 2 + ⋯
综合考虑放大器放大倍数 A A A 相对均方涨落 为
ν h A 2 = F ⋅ W E + ν A 2 + 1 J 2 \nu_{h_A}^2 = \frac{F \cdot W}{E} + \nu_A^2 + \frac{1}{J^2} ν h A 2 = E F ⋅ W + ν A 2 + J 2 1
能量分辨率 为
η = 2.355 F ⋅ W E + ν A 2 + 1 J 2 × 100 % \eta = 2.355 \sqrt{\frac{F \cdot W}{E} + \nu_A^2 + \frac{1}{J^2}} \times 100% η = 2.355 E F ⋅ W + ν A 2 + J 2 1 × 100%
因为统计涨落必然存在,所以能量分辨率不可能为 0 0 0
η statistical = 2.355 F ⋅ W E FWHM statistical = 2.355 F ⋅ W ⋅ E \eta_{\text{statistical}} = 2.355 \sqrt{\frac{F \cdot W}{E}} \ \ \ \text{FWHM}_{\text{statistical}} = 2.355 \sqrt{F \cdot W \cdot E} η statistical = 2.355 E F ⋅ W FWHM statistical = 2.355 F ⋅ W ⋅ E
其中 F ⋅ W F \cdot W F ⋅ W E E E
信号幅度 h 0 h_0 h 0 A h 0 A h_0 A h 0 A A A
综合考虑statistical与drift,则相对均方涨落
ν h A 2 = F ⋅ W E + ν A 2 \nu_{h_A}^2 = \frac{F \cdot W}{E} + \nu_A^2 ν h A 2 = E F ⋅ W + ν A 2
放大器噪声( h 2 h_2 h 2
h = h 1 + h 2 h = h_1 + h_2 h = h 1 + h 2
综合考虑statistical与drift,则相对均方涨落
ν h 2 = σ h 1 2 h 1 ‾ 2 + σ h 2 2 h 2 ‾ 2 = F ⋅ W E + 1 J 2 \nu_{h}^2 = \frac{\sigma_{h_1}^2}{\overline{h_1}^2} + \frac{\sigma_{h_2}^2}{\overline{h_2}^2} = \frac{F \cdot W}{E} + \frac{1}{J^2} ν h 2 = h 1 2 σ h 1 2 + h 2 2 σ h 2 2 = E F ⋅ W + J 2 1
其中放大器的信噪比 定义为
J = h ‾ 1 σ h 2 J = \frac{\overline{h}1}{\sigma {h_2}} J = σ h 2 h 1
能量分辨率 为
η = 2.355 F N ‾ = 2.355 F W E × 100 % \eta = 2.355 \sqrt{\frac{F}{,\overline{N},}} = 2.355 \sqrt{\frac{FW}{E}} \times 100% η = 2.355 N F = 2.355 E F W × 100%
电流电离室输出电流信号的平均值和相对均方涨落为
I ‾ = n ‾ ⋅ N ‾ ⋅ e ν I 2 = 1 + F N ‾ n ‾ ⋅ T ≈ 1 n ‾ ⋅ T \overline{I} = \overline{n} \cdot \overline{N} \cdot e \ \ \ \nu_I^2 = \frac{1+\cfrac{F}{,\overline{N},}}{\overline{n} \cdot T} \approx \frac{1}{\overline{n} \cdot T} I = n ⋅ N ⋅ e ν I 2 = n ⋅ T 1 + N F ≈ n ⋅ T 1
输出电压信号的平均值和相对均方涨落为
I ‾ = n ‾ ⋅ N ‾ ⋅ e ⋅ R 0 = I 0 R 0 ν V 2 = 1 + F N ‾ 2 R 0 C 0 n ‾ ≈ 1 2 R 0 C 0 n ‾ \overline{I} = \overline{n} \cdot \overline{N} \cdot e \cdot R_0 = I_0 R_0 \ \ \ \nu_V^2 = \frac{1+\cfrac{F}{,\overline{N},}}{2R_0C_0\overline{n}} \approx \frac{1}{2R_0C_0\overline{n}} I = n ⋅ N ⋅ e ⋅ R 0 = I 0 R 0 ν V 2 = 2 R 0 C 0 n 1 + N F ≈ 2 R 0 C 0 n 1
累计信号的相对均方涨落有如下特点:
主要决定于入射粒子数 n n n
离子对数 N N N
正比计数器的输出脉冲幅度 h h h
h ∼ N A e C 0 h \sim \frac{NAe}{C_0} h ∼ C 0 N A e
相对均方涨落 为
ν h 2 = ν N 2 + 1 N ‾ ν A 2 = F N ‾ + 1 N ‾ ν A 2 \nu_h^2 = \nu_N^2 + \frac{1}{,\overline{N},} \nu_A^2 = \frac{F}{,\overline{N},} + \frac{1}{,\overline{N},} \nu_A^2 ν h 2 = ν N 2 + N 1 ν A 2 = N F + N 1 ν A 2
其中实验测得 ν A 2 ≈ 0.68 \nu_A^2 \approx 0.68 ν A 2 ≈ 0.68 能量分辨率 为
η = 2.355 F + 0.68 N ‾ × 100 % \eta = 2.355 \sqrt{\frac{F+0.68}{\overline{N}}} \times 100% η = 2.355 N F + 0.68 × 100%
光电倍增管PMT的倍增系数 M M M 相对均方涨落 为
ν M 2 = δ δ 1 ( 1 δ − 1 ) \nu_M^2 = \frac{\delta}{\delta_1} \left( \frac{1}{\delta-1} \right) ν M 2 = δ 1 δ ( δ − 1 1 )
其中 δ 1 \delta_1 δ 1 δ \delta δ
能量分辨率 为
η = 2.355 1 n ‾ e [ 1 + δ δ 1 ( 1 δ − 1 ) ] \eta = 2.355 \sqrt{\frac{1}{\overline{n}_e} \left[ 1 + \frac{\delta}{\delta_1} \left( \frac{1}{\delta-1} \right) \right] } η = 2.355 n e 1 [ 1 + δ 1 δ ( δ − 1 1 ) ]
其中 n e = E Y ph T n_e = E Y_{\text{ph}} T n e = E Y ph T
只考虑统计涨落的能量分辨率 为
η = 2.355 F N ‾ = 2.355 F W E \eta = 2.355 \sqrt{\frac{F}{,\overline{N},}} = 2.355 \sqrt{\frac{FW}{E}} η = 2.355 N F = 2.355 E F W
考虑电荷灵敏前置放大器的噪声:
Δ E noise = Δ E 零电容 + Δ E 电容噪声 = Δ E 零电容 + 噪声斜率 × 探测器电容 \Delta E_{\text{noise}} = \Delta E_{\text{零电容}} + \Delta E_{\text{电容噪声}} = \Delta E_{\text{零电容}} + \text{噪声斜率} \times \text{探测器电容} Δ E noise = Δ E 零电容 + Δ E 电容噪声 = Δ E 零电容 + 噪声斜率 × 探测器电容
也可以用等效噪声电荷 ENC \text{ENC} ENC
Δ E noise = 2.355 ⋅ W ⋅ ENC \Delta E_{\text{noise}} = 2.355 \cdot W \cdot \text{ENC} Δ E noise = 2.355 ⋅ W ⋅ ENC
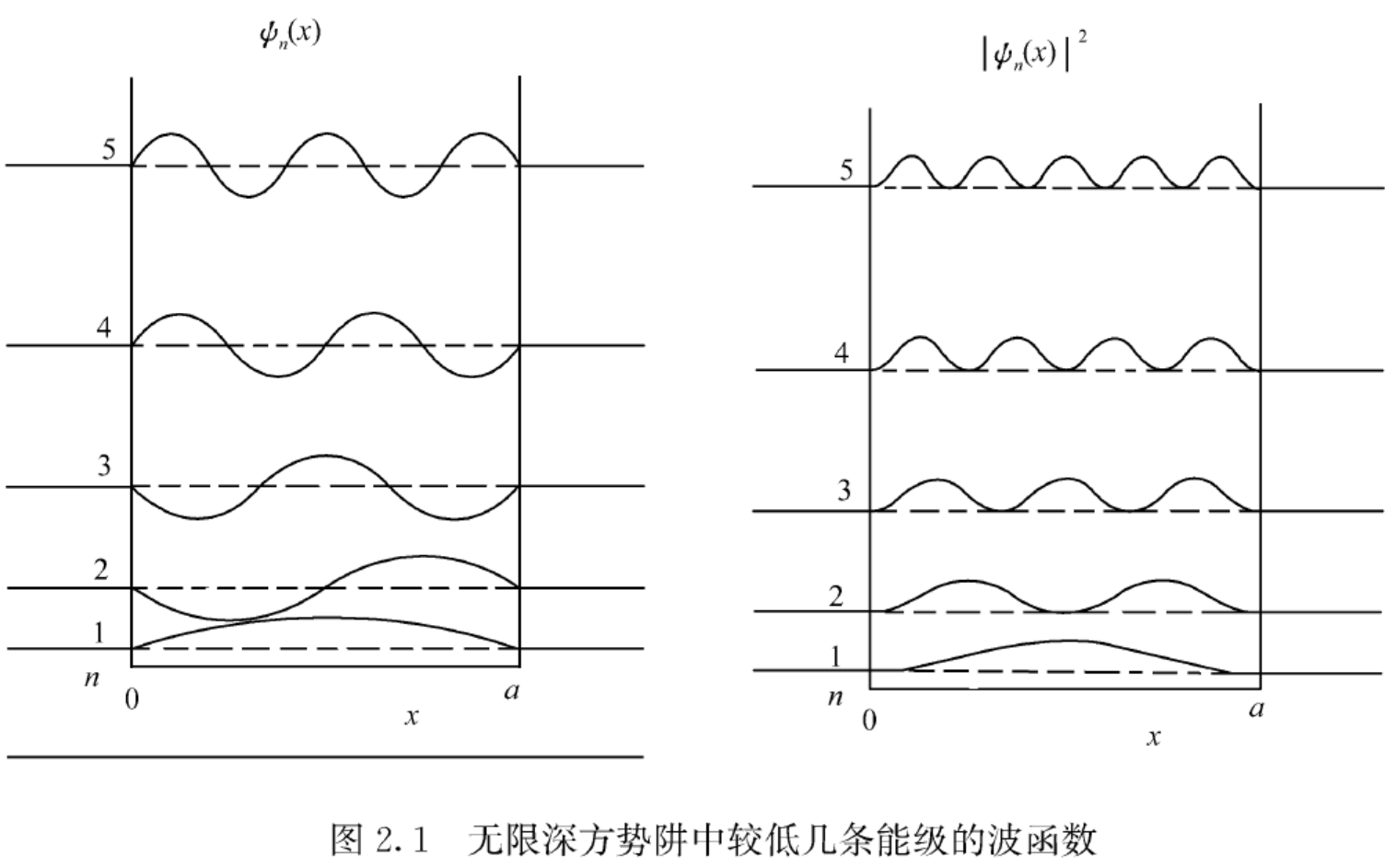
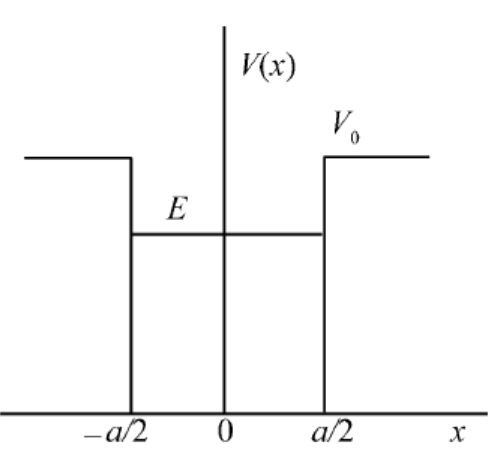
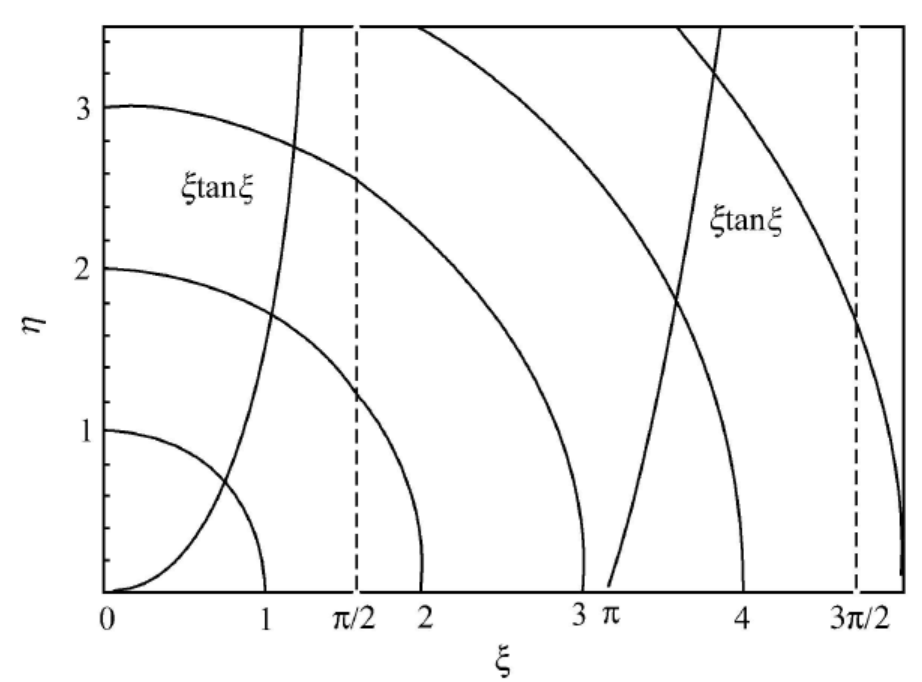
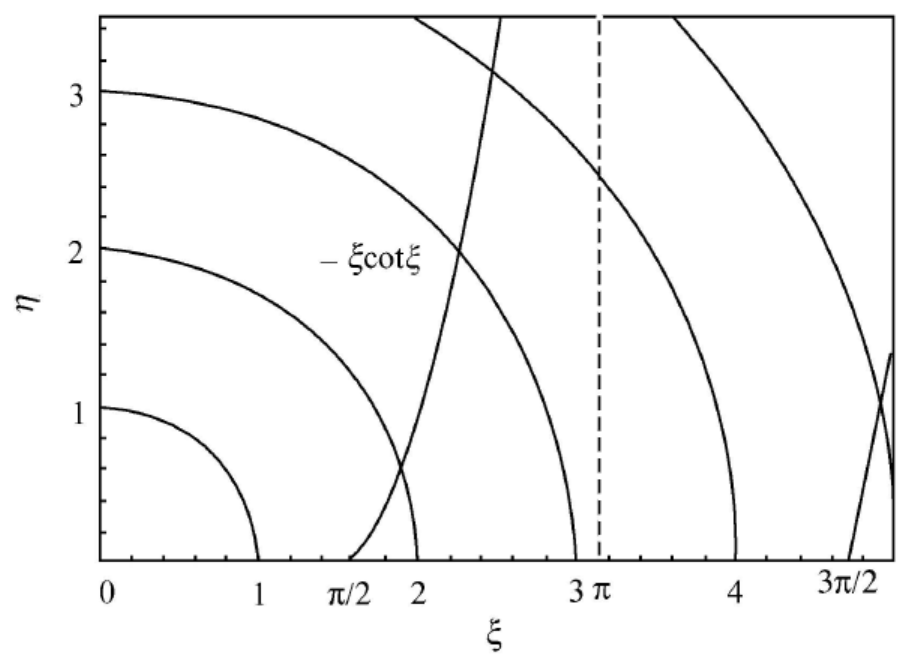
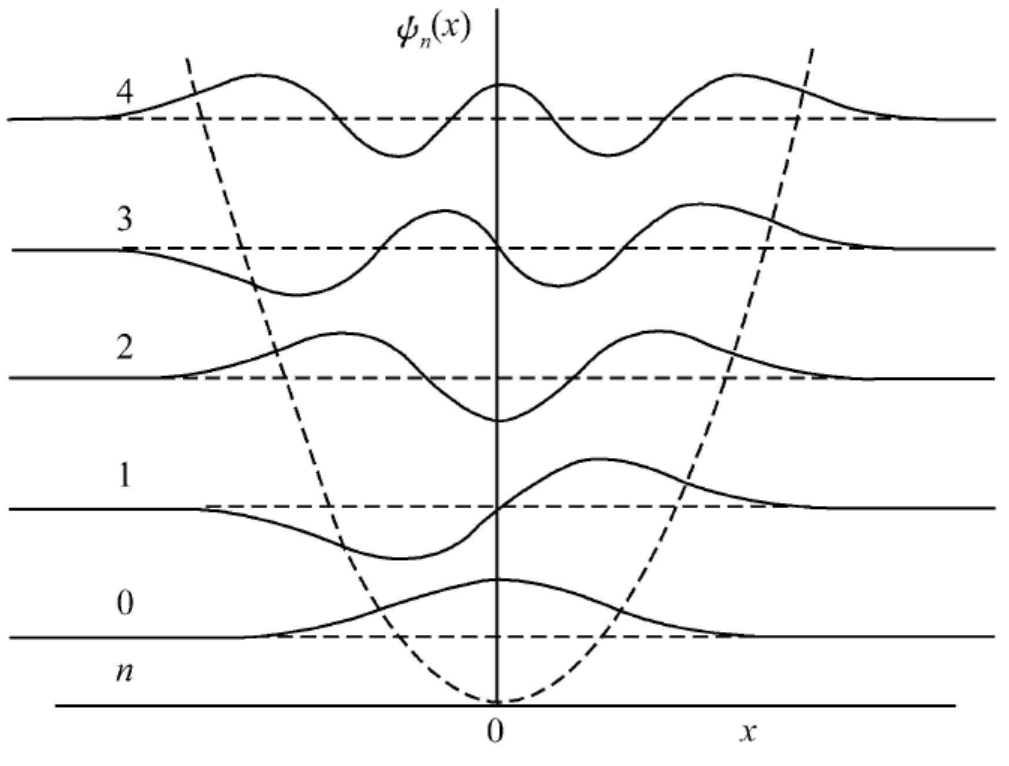
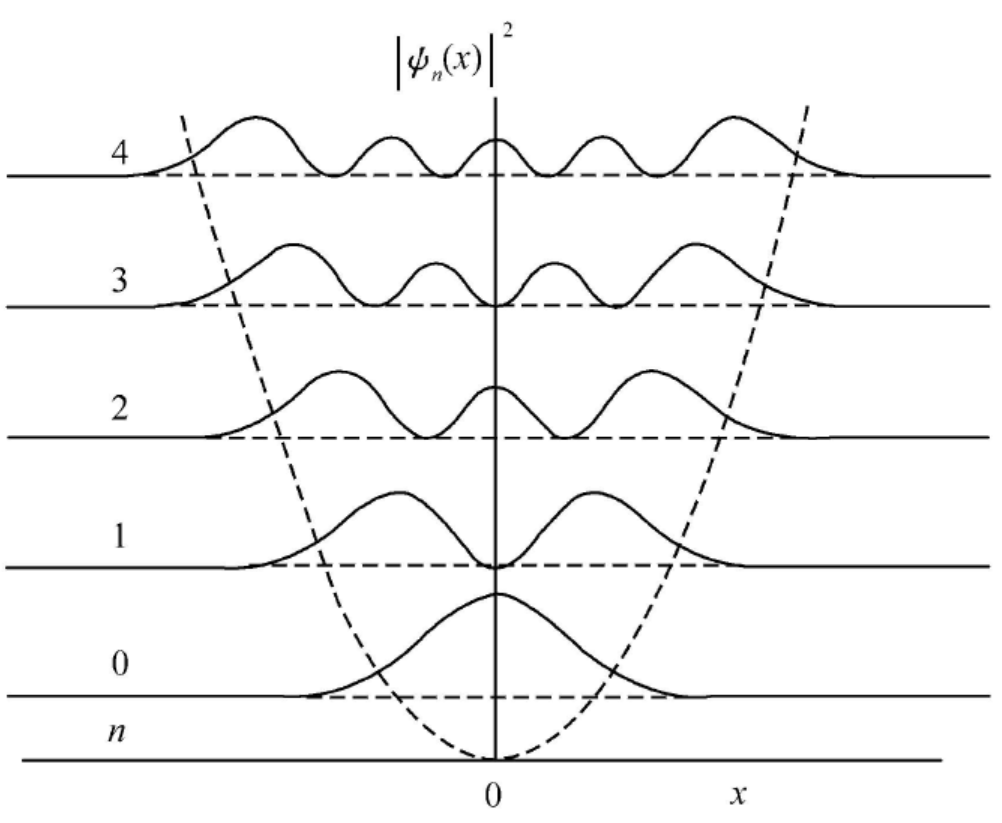
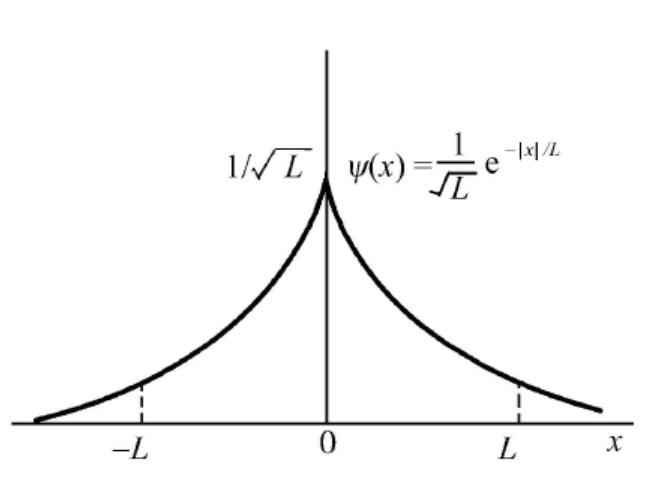
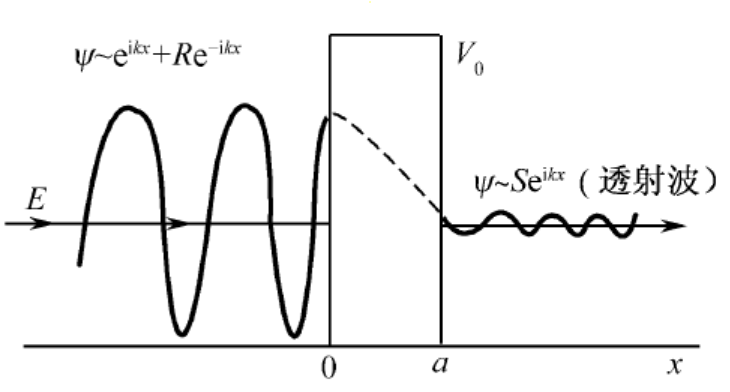
.png)