对于任意已归一化的波函数 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) A A A A ˉ = ( ψ , A ^ ψ ) \bar{A} = (\psi , \hat{A}\psi) A ˉ = ( ψ , A ^ ψ ) H ^ ψ = i ℏ ∂ ∂ t ψ \hat{H} \psi = \mathrm{i}\hbar \frac{\partial}{\partial t} \psi H ^ ψ = i ℏ ∂ t ∂ ψ
d d t A ˉ ( t ) = ( ∂ ψ ∂ t , A ^ ψ ) + ( ψ , A ^ ∂ ψ ∂ t ) + ( ψ , ∂ A ^ ∂ t ψ ) = ( H ^ ψ i ℏ , A ^ ψ ) + ( ψ , A ^ H ^ ψ i ℏ ) + ( ψ , ∂ A ^ ∂ t ψ ) = − 1 i ℏ ( ψ , H ^ A ^ ψ ) + 1 i ℏ ( ψ , A ^ H ^ ψ ) + ( ψ , ∂ A ^ ∂ t ψ ) = 1 i ℏ ( ψ , [ A ^ , H ^ ] ψ ) + ( ψ , ∂ A ^ ∂ t ψ ) = 1 i ℏ [ A ^ , H ^ ] ‾ + ∂ A ^ ∂ t ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A}(t) = \left( \frac{\partial \psi}{\partial t} , \hat{A} \psi \right) + \left( \psi , \hat{A} \frac{\partial \psi}{\partial t} \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = \left( \frac{\hat{H} \psi}{\mathrm{i}\hbar} , \hat{A} \psi \right) + \left( \psi , \hat{A} \frac{\hat{H} \psi}{\mathrm{i}\hbar} \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = -\frac{1}{\mathrm{i}\hbar} \left( \psi , \hat{H} \hat{A} \psi \right) + \frac{1}{\mathrm{i}\hbar} \left( \psi , \hat{A} \hat{H} \psi \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( \psi , [\hat{A} , \hat{H}] \psi \right) + \left( \psi , \frac{\partial \hat{A}}{\partial t} \psi \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A} , \hat{H}]} + \overline{\frac{\partial \hat{A}}{\partial t}} d t d A ˉ ( t ) = ( ∂ t ∂ ψ , A ^ ψ ) + ( ψ , A ^ ∂ t ∂ ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = ( i ℏ H ^ ψ , A ^ ψ ) + ( ψ , A ^ i ℏ H ^ ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = − i ℏ 1 ( ψ , H ^ A ^ ψ ) + i ℏ 1 ( ψ , A ^ H ^ ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = i ℏ 1 ( ψ , [ A ^ , H ^ ] ψ ) + ( ψ , ∂ t ∂ A ^ ψ ) = i ℏ 1 [ A ^ , H ^ ] + ∂ t ∂ A ^
如果 A ^ \hat{A} A ^ t t t ∂ A ^ ∂ t = 0 \frac{\partial \hat{A}}{\partial t} = 0 ∂ t ∂ A ^ = 0
d d t A ˉ = 1 i ℏ [ A ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A} = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A} , \hat{H}]} d t d A ˉ = i ℏ 1 [ A ^ , H ^ ]
因此,若
[ A ^ , H ^ ] = 0 [\hat{A} , \hat{H}] = 0 [ A ^ , H ^ ] = 0
则
d d t A ˉ = 0 \frac{\mathrm{d}}{\mathrm{d}t} \bar{A} = 0 d t d A ˉ = 0
即这种力学量在任何态 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) 平均值都不随时间改变 。进一步考虑其概率分布,因为 [ A ^ , H ^ ] = 0 [\hat{A} , \hat{H}] = 0 [ A ^ , H ^ ] = 0 H ^ \hat{H} H ^ A ^ \hat{A} A ^ ψ k \psi_k ψ k
H ^ ψ k = E k ψ k , A ^ ψ k = A k ψ k \hat{H} \psi_k = E_k \psi_k \ , \kern 1em \hat{A} \psi_k = A_k \psi_k H ^ ψ k = E k ψ k , A ^ ψ k = A k ψ k
这样,体系的任何(已归一化的)态 ψ ( r ⃗ , t ) \psi(\vec{r},t) ψ ( r , t ) ψ k \psi_k ψ k
ψ ( r ⃗ , t ) = ∑ k a k ( t ) ψ k ( r ⃗ ) \psi(\vec{r},t) = \sum_k a_k(t)\psi_k(\vec{r}) ψ ( r , t ) = k ∑ a k ( t ) ψ k ( r )
展开系数 a k ( t ) = ( ψ k , ψ ) a_k(t) = (\psi_k , \psi) a k ( t ) = ( ψ k , ψ ) ψ \psi ψ t t t A A A A k A_k A k ∣ a k ( t ) ∣ 2 |a_k(t)|^2 ∣ a k ( t ) ∣ 2
d d t ∣ a k ( t ) ∣ 2 = d d t [ a k ∗ ( t ) a k ( t ) ] = a k ( t ) d a k ∗ ( t ) d t + a k ∗ ( t ) d a k ( t ) d t = ( ψ k , ψ ) ( ∂ ψ ∂ t , ψ k ) + 复共轭项 = ( ψ k , ψ ) ( H ^ ψ i ℏ , ψ k ) + 复共轭项 = − 1 i ℏ ( ψ k , ψ ) ( H ^ ψ , ψ k ) + 复共轭项 = − 1 i ℏ ( ψ k , ψ ) ( ψ , H ^ ψ k ) + 复共轭项 = − E k i ℏ ( ψ k , ψ ) ( ψ , ψ k ) + 复共轭项 = − E k i ℏ ∣ ( ψ k , ψ ) ∣ 2 + 复共轭项 = 0 \frac{\mathrm{d}}{\mathrm{d}t} |a_k(t)|^2 = \frac{\mathrm{d}}{\mathrm{d}t} [a_k^(t) a_k(t)] = a_k(t) \frac{\mathrm{d}a_k^ (t)}{\mathrm{d}t} + a_k^*(t) \frac{\mathrm{d}a_k(t)}{\mathrm{d}t} \ \ \ = (\psi_k , \psi) \left( \frac{\partial \psi}{\partial t} , \psi_k \right) + 复共轭项 \ \ \ = (\psi_k , \psi) \left( \frac{\hat{H} \psi}{\mathrm{i}\hbar} , \psi_k \right) + 复共轭项 \ \ \ = -\frac{1}{\mathrm{i}\hbar} (\psi_k , \psi) (\hat{H} \psi , \psi_k) + 复共轭项 \ \ \ = -\frac{1}{\mathrm{i}\hbar} (\psi_k , \psi) (\psi , \hat{H} \psi_k) + 复共轭项 \ \ \ = -\frac{E_k}{\mathrm{i}\hbar} (\psi_k , \psi) (\psi , \psi_k) + 复共轭项 \ \ \ = -\frac{E_k}{\mathrm{i}\hbar} \left| (\psi_k , \psi) \right|^2 + 复共轭项 \ \ \ = 0 d t d ∣ a k ( t ) ∣ 2 = d t d [ a k ∗ ( t ) a k ( t )] = a k ( t ) d t d a k ∗ ( t ) + a k ∗ ( t ) d t d a k ( t ) = ( ψ k , ψ ) ( ∂ t ∂ ψ , ψ k ) + 复共轭项 = ( ψ k , ψ ) ( i ℏ H ^ ψ , ψ k ) + 复共轭项 = − i ℏ 1 ( ψ k , ψ ) ( H ^ ψ , ψ k ) + 复共轭项 = − i ℏ 1 ( ψ k , ψ ) ( ψ , H ^ ψ k ) + 复共轭项 = − i ℏ E k ( ψ k , ψ ) ( ψ , ψ k ) + 复共轭项 = − i ℏ E k ∣ ( ψ k , ψ ) ∣ 2 + 复共轭项 = 0
故 A A A 概率分布不随时间改变 。
对于Hamilton量 H ^ \hat{H} H ^ [ A ^ , H ^ ] = 0 [\hat{A},\hat{H}]=0 [ A ^ , H ^ ] = 0 A ^ \hat{A} A ^ H ^ \hat{H} H ^ 对易 ,则在体系的任意态(定态或非定态)上, A A A 平均值及其取值概率分布都不随时间改变 。量子力学把这些在体系的任意状态上的平均值和取值概率分布都不随时间改变的力学量,称为该体系的守恒量 。
如果体系的Hamilton量不显含时间 t t t ∂ H ^ ∂ t = 0 \frac{\partial \hat{H}}{\partial t} = 0 ∂ t ∂ H ^ = 0 H ^ \hat{H} H ^ 对易守恒量完全集 (a complete set of commuting conserved observables,简记为CSCCO)。
包括 H ^ \hat{H} H ^ 定态 ,所相应的量子数为好量子数 ,任意波函数 ψ \psi ψ ∣ a α ∣ 2 |a_\alpha|^2 ∣ a α ∣ 2
以三维各向同性谐振子为例,CSCCO可取为 { H ^ , L ^ 2 , L ^ z } { \hat{H} , \hat{L}^2 , \hat{L}_z } { H ^ , L ^ 2 , L ^ z } L ^ z \hat{L}_z L ^ z L ^ x \hat{L}_x L ^ x L ^ y \hat{L}_y L ^ y { H ^ x , H ^ y , H ^ z } { \hat{H}_x , \hat{H}_y , \hat{H}_z } { H ^ x , H ^ y , H ^ z }
与经典力学守恒量不同,量子体系的守恒量并不一定取确定值,即体系的状态并不一定就是某个守恒量的本征态,可以保证的只是守恒量的平均值及其取值概率分布都不随时间改变。
即使是在定态(能量本征态)上,守恒量也不一定取确定值,定态只能保证能量取确定值。
若初始时刻体系处于守恒量 A ^ \hat{A} A ^ 保持在该本征态 ,守恒量将取确定值。由于守恒量具有此特点,它的量子数称为好量子数 。
若初始时刻体系并不处于守恒量 A ^ \hat{A} A ^ A ^ \hat{A} A ^ A ^ \hat{A} A ^
量子力学中习惯用描述力学量本征值的量子数来标志状态,但非守恒量的量子数不适合描述状态,只有守恒量的量子数才是描述状态的好量子数。
由于量子体系的各守恒量只要求与Hamilton量 H ^ \hat{H} H ^
定态 是体系的一种特殊的状态,即能量本征态 ;而守恒量 则是体系的一种特殊的力学量,它与体系的Hamilton量对易。
在定态 上,一切力学量 (只要不显含时间 t t t
而守恒量 在一切状态 上(不管是否是定态)的平均值和取值概率分布都不随时间变化。
如果体系具有两个互相不对易的守恒量 F ^ , G ^ \hat{F},\hat{G} F ^ , G ^ [ F ^ , H ^ ] = [ G ^ , H ^ ] = 0 [\hat{F},\hat{H}] = [\hat{G},\hat{H}] = 0 [ F ^ , H ^ ] = [ G ^ , H ^ ] = 0 [ F ^ , G ^ ] ≠ 0 [\hat{F},\hat{G}] \ne 0 [ F ^ , G ^ ] = 0 简并 的。
在一般情况下,当能级出现简并时,可以根据对体系对称性的分析,找出其守恒量。然后要求能量本征态同时又是包含 H ^ \hat{H} H ^
由于 [ F ^ , H ^ ] = 0 [\hat{F},\hat{H}] = 0 [ F ^ , H ^ ] = 0 F ^ \hat{F} F ^ H ^ \hat{H} H ^ ψ \psi ψ
H ^ ψ = E ψ , F ^ ψ = λ ψ \hat{H} \psi = E \psi \ , \kern 1em \hat{F} \psi = \lambda \psi H ^ ψ = E ψ , F ^ ψ = λ ψ
考虑到 [ G ^ , H ^ ] = 0 [\hat{G},\hat{H}] = 0 [ G ^ , H ^ ] = 0
H ^ ( G ^ ψ ) = H ^ G ^ ψ = G ^ H ^ ψ = G ^ E ψ = E ( G ^ ψ ) \hat{H} (\hat{G} \psi) = \hat{H} \hat{G} \psi = \hat{G} \hat{H} \psi = \hat{G} E \psi = E (\hat{G} \psi) H ^ ( G ^ ψ ) = H ^ G ^ ψ = G ^ H ^ ψ = G ^ E ψ = E ( G ^ ψ )
即 G ^ ψ \hat{G}\psi G ^ ψ H ^ \hat{H} H ^ E E E [ F ^ , G ^ ] ≠ 0 [\hat{F},\hat{G}] \ne 0 [ F ^ , G ^ ] = 0
F ^ ( G ^ ψ ) = F ^ G ^ ψ ≠ G ^ F ^ ψ = G ^ λ ψ = λ G ^ ψ \hat{F} (\hat{G} \psi) = \hat{F} \hat{G} \psi \ne \hat{G} \hat{F} \psi = \hat{G} \lambda \psi = \lambda \hat{G} \psi F ^ ( G ^ ψ ) = F ^ G ^ ψ = G ^ F ^ ψ = G ^ λ ψ = λ G ^ ψ
即 G ^ ψ \hat{G}\psi G ^ ψ F ^ \hat{F} F ^ ψ \psi ψ F ^ \hat{F} F ^ G ^ ψ \hat{G}\psi G ^ ψ ψ \psi ψ H ^ \hat{H} H ^ E E E
如果体系有一个守恒量 F ^ \hat{F} F ^ E E E ψ E \psi_E ψ E ψ E \psi_E ψ E F ^ \hat{F} F ^
这是因为
H ^ ( F ^ ψ E ) = H ^ F ^ ψ E = F ^ H ^ ψ E = F ^ E ψ E = E ( F ^ ψ E ) \hat{H} (\hat{F} \psi_E) = \hat{H} \hat{F} \psi_E = \hat{F} \hat{H} \psi_E = \hat{F} E \psi_E = E (\hat{F} \psi_E) H ^ ( F ^ ψ E ) = H ^ F ^ ψ E = F ^ H ^ ψ E = F ^ E ψ E = E ( F ^ ψ E )
即 ψ E \psi_E ψ E H ^ \hat{H} H ^ E E E E E E F ^ ψ E \hat{F}\psi_E F ^ ψ E ψ E \psi_E ψ E λ \lambda λ F ^ ψ E = λ ψ E \hat{F} \psi_E = \lambda \psi_E F ^ ψ E = λ ψ E ψ E \psi_E ψ E F ^ \hat{F} F ^
对于上述的“一般”,虽然 [ F ^ , G ^ ] ≠ 0 [\hat{F},\hat{G}] \ne 0 [ F ^ , G ^ ] = 0 F ^ \hat{F} F ^ G ^ \hat{G} G ^ [ F ^ , G ^ ] ψ 0 = 0 [\hat{F},\hat{G}]\psi_0 = 0 [ F ^ , G ^ ] ψ 0 = 0 ψ 0 \psi_0 ψ 0 G ^ ψ 0 \hat{G}\psi_0 G ^ ψ 0 ψ 0 \psi_0 ψ 0 ψ 0 \psi_0 ψ 0 [ F ^ , G ^ ] [\hat{F},\hat{G}] [ F ^ , G ^ ]
例如:中心力场下, L ⃗ ^ \hat{\vec{L}} L ^ L ^ x , L ^ y , L ^ z \hat{L}_x , \hat{L}_y , \hat{L}_z L ^ x , L ^ y , L ^ z s s s l = 0 l=0 l = 0 L x , L y , L z L_x , L_y , L_z L x , L y , L z 0 0 0 L ^ x ψ s = L ^ y ψ s = L ^ z ψ s = 0 \hat{L}_x \psi_s = \hat{L}_y \psi_s = \hat{L}_z \psi_s = 0 L ^ x ψ s = L ^ y ψ s = L ^ z ψ s = 0 [ L ^ x , L ^ y ] ψ s = [ L ^ y , L ^ z ] ψ s = [ L ^ z , L ^ x ] ψ s = 0 [\hat{L}_x , \hat{L}_y] \psi_s = [\hat{L}_y , \hat{L}_z] \psi_s = [\hat{L}_z , \hat{L}_x] \psi_s = 0 [ L ^ x , L ^ y ] ψ s = [ L ^ y , L ^ z ] ψ s = [ L ^ z , L ^ x ] ψ s = 0 ψ s \psi_s ψ s l = 0 l=0 l = 0
位力定理可以描述当体系处于定态 下时平均值关于时间的变化。
设粒子处于势场 V ( r ⃗ ) V(\vec{r}) V ( r )
H ^ = p ⃗ ^ 2 2 m + V ( r ⃗ ) \hat{H} = \frac{\hat{\vec{p}}^2}{2m} + V(\vec{r}) H ^ = 2 m p ^ 2 + V ( r )
则粒子的动能算符 T ^ = p ⃗ ^ 2 / ( 2 m ) \hat{T} = \hat{\vec{p}}^2 /(2m) T ^ = p ^ 2 / ( 2 m ) 定态 上的平均值为
T ˉ = 1 2 r ⃗ ⋅ ∇ V ‾ \bar{T} = \frac12 \overline{\vec{r} \cdot \nabla V } T ˉ = 2 1 r ⋅ ∇ V
先考虑 r ⃗ ⋅ p ⃗ \vec{r} \cdot \vec{p}, r ⋅ p ∂ ∂ t ( r ⃗ ^ ⋅ p ⃗ ^ ) = 0 \frac{\partial}{\partial t} (\hat{\vec{r}}\cdot\hat{\vec{p}})=0 ∂ t ∂ ( r ^ ⋅ p ^ ) = 0 r ⃗ ^ ⋅ p ⃗ ^ \hat{\vec{r}} \cdot \hat{\vec{p}}, r ^ ⋅ p ^ 1 2 ( r ⃗ ^ ⋅ p ⃗ ^ + p ⃗ ^ ⋅ r ⃗ ^ ) \frac12(\hat{\vec{r}}\cdot\hat{\vec{p}} + \hat{\vec{p}}\cdot\hat{\vec{r}}) 2 1 ( r ^ ⋅ p ^ + p ^ ⋅ r ^ ) A ^ \hat{A} A ^
d d t A ˉ = 1 i ℏ [ A ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A} = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A} , \hat{H}]} d t d A ˉ = i ℏ 1 [ A ^ , H ^ ]
可知
d d t r ⃗ ⋅ p ⃗ ‾ = 1 i ℏ [ r ⃗ ^ ⋅ p ⃗ ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \overline{\vec{r}\cdot\vec{p}} = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{H}]} d t d r ⋅ p = i ℏ 1 [ r ^ ⋅ p ^ , H ^ ]
其中
[ r ⃗ ^ ⋅ p ⃗ ^ , H ^ ] ‾ = [ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 2 m + V ( r ⃗ ) ] ‾ = 1 2 m [ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 ] ‾ + [ r ⃗ ^ ⋅ p ⃗ ^ , V ( r ⃗ ) ] ‾ \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{H}]} = \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \frac{\hat{\vec{p}}^2}{2m} + V(\vec{r})]} \ \ \ = \frac{1}{2m} \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{\vec{p}}^2]} + \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , V(\vec{r})]} [ r ^ ⋅ p ^ , H ^ ] = [ r ^ ⋅ p ^ , 2 m p ^ 2 + V ( r )] = 2 m 1 [ r ^ ⋅ p ^ , p ^ 2 ] + [ r ^ ⋅ p ^ , V ( r )]
其中的第一个对易关系可通过分量展开考虑
[ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 ] = r ⃗ ^ ⋅ [ p ⃗ ^ , p ⃗ ^ 2 ] + [ r ⃗ ^ , p ⃗ ^ 2 ] ⋅ p ⃗ ^ = [ r ⃗ ^ , p ⃗ ^ 2 ] ⋅ p ⃗ ^ = ( [ x ^ , p x 2 ^ ] i ⃗ + [ y ^ , p y 2 ^ ] j ⃗ + [ z ^ , p z 2 ^ ] k ⃗ ) ⋅ p ⃗ ^ = { ( p ^ x [ x ^ , p ^ x ] + [ x ^ , p ^ x ] p ^ x ) i ⃗ + ( p ^ y [ y ^ , p ^ y ] + [ y ^ , p ^ y ] p ^ y ) j ⃗ + ( p ^ z [ z ^ , p ^ z ] + [ z ^ , p ^ z ] p ^ z ) k ⃗ } ⋅ p ⃗ ^ = 2 i ℏ ( p ^ x i ⃗ + p ^ y j ⃗ + p ^ z k ⃗ ) ⋅ p ⃗ ^ = 2 i ℏ p ⃗ ^ 2 [\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{\vec{p}}^2] = \hat{\vec{r}}\cdot [\hat{\vec{p}} , \hat{\vec{p}}^2] + [\hat{\vec{r}} , \hat{\vec{p}}^2] \cdot\hat{\vec{p}} = [\hat{\vec{r}} , \hat{\vec{p}}^2] \cdot\hat{\vec{p}} \ \ \ = \left( [\hat{x},\hat{p_x^2}] \vec{i} + [\hat{y},\hat{p_y^2}] \vec{j} + [\hat{z},\hat{p_z^2}] \vec{k} \right) \cdot\hat{\vec{p}} \ \ \ = \left{ \left( \hat{p}_x [\hat{x},\hat{p}_x] + [\hat{x},\hat{p}_x] \hat{p}_x \right) \vec{i} + \left( \hat{p}_y [\hat{y},\hat{p}_y] + [\hat{y},\hat{p}_y] \hat{p}_y \right) \vec{j} + \left( \hat{p}_z [\hat{z},\hat{p}_z] + [\hat{z},\hat{p}_z] \hat{p}_z \right) \vec{k} \right} \cdot\hat{\vec{p}} \ \ \ = 2\mathrm{i} \hbar \left( \hat{p}_x \vec{i} + \hat{p}_y \vec{j} + \hat{p}_z \vec{k} \right) \cdot\hat{\vec{p}} \ \ \ = 2\mathrm{i} \hbar \hat{\vec{p}}^2 [ r ^ ⋅ p ^ , p ^ 2 ] = r ^ ⋅ [ p ^ , p ^ 2 ] + [ r ^ , p ^ 2 ] ⋅ p ^ = [ r ^ , p ^ 2 ] ⋅ p ^ = ( [ x ^ , p x 2 ^ ] i + [ y ^ , p y 2 ^ ] j + [ z ^ , p z 2 ^ ] k ) ⋅ p ^ = { ( p ^ x [ x ^ , p ^ x ] + [ x ^ , p ^ x ] p ^ x ) i + ( p ^ y [ y ^ , p ^ y ] + [ y ^ , p ^ y ] p ^ y ) j + ( p ^ z [ z ^ , p ^ z ] + [ z ^ , p ^ z ] p ^ z ) k } ⋅ p ^ = 2 i ℏ ( p ^ x i + p ^ y j + p ^ z k ) ⋅ p ^ = 2 i ℏ p ^ 2
第二个对易关系可通过在坐标表象下作用波函数考虑
[ r ⃗ ^ ⋅ p ⃗ ^ , V ( r ⃗ ) ] ψ = − i ℏ [ r ⃗ ⋅ ∇ , V ( r ⃗ ) ] ψ = − i ℏ r ⃗ ⋅ [ ∇ , V ( r ⃗ ) ] ψ − i ℏ [ r ⃗ , V ( r ⃗ ) ] ⋅ ∇ ψ = − i ℏ r ⃗ ⋅ { ∇ ( V ( r ⃗ ) ψ ) − V ( r ⃗ ) ∇ ψ } = − i ℏ r ⃗ ⋅ ( ∇ V ( r ⃗ ) ) ψ [\hat{\vec{r}}\cdot\hat{\vec{p}} , V(\vec{r})] \psi = -\mathrm{i} \hbar [\vec{r}\cdot\nabla , V(\vec{r})] \psi \ \ \ = -\mathrm{i} \hbar \vec{r}\cdot [\nabla , V(\vec{r})] \psi -\mathrm{i} \hbar [\vec{r} , V(\vec{r})] \cdot\nabla \psi \ \ \ = -\mathrm{i} \hbar \vec{r}\cdot \left{ \nabla\left(V(\vec{r})\psi\right) - V(\vec{r}) \nabla\psi \right} \ \ \ = -\mathrm{i} \hbar \vec{r}\cdot \left( \nabla V(\vec{r}) \right) \psi [ r ^ ⋅ p ^ , V ( r )] ψ = − i ℏ [ r ⋅ ∇ , V ( r )] ψ = − i ℏ r ⋅ [ ∇ , V ( r )] ψ − i ℏ [ r , V ( r )] ⋅ ∇ ψ = − i ℏ r ⋅ { ∇ ( V ( r ) ψ ) − V ( r ) ∇ ψ } = − i ℏ r ⋅ ( ∇ V ( r ) ) ψ
故
[ r ⃗ ^ ⋅ p ⃗ ^ , H ^ ] ‾ = 1 2 m [ r ⃗ ^ ⋅ p ⃗ ^ , p ⃗ ^ 2 ] ‾ + [ r ⃗ ^ ⋅ p ⃗ ^ , V ( r ⃗ ) ] ‾ = 1 2 m 2 i ℏ p ⃗ 2 ‾ + − i ℏ r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ = i ℏ [ 2 p ⃗ 2 2 m ‾ − r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ ] = i ℏ [ 2 T ‾ − r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ ] \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{H}]} = \frac{1}{2m} \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , \hat{\vec{p}}^2]} + \overline{[\hat{\vec{r}}\cdot\hat{\vec{p}} , V(\vec{r})]} \ \ \ = \frac{1}{2m} \overline{2\mathrm{i} \hbar \vec{p}^2} + \overline{-\mathrm{i} \hbar \vec{r}\cdot \nabla V(\vec{r})} \ \ \ = \mathrm{i} \hbar \left[ 2 \overline{\frac{\vec{p}^2}{2m}} - \overline{\vec{r}\cdot\nabla V(\vec{r})} \right] \ \ \ = \mathrm{i} \hbar \left[ 2 \overline{T} - \overline{\vec{r}\cdot\nabla V(\vec{r})} \right] [ r ^ ⋅ p ^ , H ^ ] = 2 m 1 [ r ^ ⋅ p ^ , p ^ 2 ] + [ r ^ ⋅ p ^ , V ( r )] = 2 m 1 2 i ℏ p 2 + − i ℏ r ⋅ ∇ V ( r ) = i ℏ [ 2 2 m p 2 − r ⋅ ∇ V ( r ) ] = i ℏ [ 2 T − r ⋅ ∇ V ( r ) ]
对于定态,有
d d t r ⃗ ⋅ p ⃗ ‾ = 0 \frac{\mathrm{d}}{\mathrm{d}t} \overline{\vec{r}\cdot\vec{p}} = 0 d t d r ⋅ p = 0
故
2 T ‾ − r ⃗ ⋅ ∇ V ( r ⃗ ) ‾ = 0 2 \overline{T} - \overline{\vec{r}\cdot\nabla V(\vec{r})} = 0 2 T − r ⋅ ∇ V ( r ) = 0
若 V ( r ⃗ ) V(\vec{r}) V ( r ) x , y , z x,y,z x , y , z n n n V ( c x , c y , c z ) = c n V ( x , y , z ) V(cx,cy,cz) = c^n V(x,y,z) V ( c x , cy , cz ) = c n V ( x , y , z ) c c c
r ⃗ ⋅ ∇ V ( r ⃗ ) = n V ( r ⃗ ) \vec{r}\cdot\nabla V(\vec{r}) = n V(\vec{r}) r ⋅ ∇ V ( r ) = nV ( r )
证明可见杨利军老师微积分A2第二次习题课 第6题。
故
2 T ˉ = n V ˉ 2 \bar{T} = n \bar{V} 2 T ˉ = n V ˉ
如对于谐振子势 V ( r ⃗ ) = 1 2 m ω 2 r 2 V(\vec{r}) = \frac12 m\omega^2 r^2 V ( r ) = 2 1 m ω 2 r 2 n = 2 n=2 n = 2 T ˉ = V ˉ \bar{T} = \bar{V} T ˉ = V ˉ V ( r ⃗ ) = − k Z e 2 r V(\vec{r}) = -\frac{kZe^2}{r} V ( r ) = − r k Z e 2 n = − 1 n=-1 n = − 1 T ˉ = − 1 2 V ˉ \bar{T} = -\frac12 \bar{V} T ˉ = − 2 1 V ˉ E ˉ = T ˉ + V ˉ = 1 2 V ˉ \bar{E} = \bar{T} + \bar{V} = \frac12 \bar{V} E ˉ = T ˉ + V ˉ = 2 1 V ˉ
这里的图像 (picture)也叫绘景 ,亦称表象 (representation)。由于状态和力学量本身并不能直接测量,能直接测量的是力学量的平均值,因此可以用不同方式描述状态和力学量随时间的演化 ,只要保证力学量的平均值不因描述方式的不同而改变取值即可。
态矢 ψ ( t ) \psi(t) ψ ( t ) 随时间演化 ,其变化遵守Schrödinger方程,力学量算符 (不显含时间 t t t 与时间无关 ,即把力学量平均值及测值概率分布随时间的演化完全归之于波函数的演化,这种描述方式称为Schrödinger图像 。即
A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ) ) \bar{A}(t) = (\psi(t) , \hat{A} \psi(t)) A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ))
其中 ψ ( t ) \psi(t) ψ ( t )
i ℏ ∂ ∂ t ψ ( t ) = H ^ ψ ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(t) = \hat{H} \psi(t) i ℏ ∂ t ∂ ψ ( t ) = H ^ ψ ( t )
由此可以得到
d d t A ˉ ( t ) = 1 i ℏ [ A ^ , H ^ ] ‾ \frac{\mathrm{d}}{\mathrm{d}t} \bar{A}(t) = \frac{1}{\mathrm{i}\hbar} \overline{[\hat{A},\hat{H}]} d t d A ˉ ( t ) = i ℏ 1 [ A ^ , H ^ ]
态矢 ψ \psi ψ 不随时间变化 ,而力学量算符随时间变化 ,其变化遵守Heisenberg方程,即把力学量平均值及测值概率分布随时间的演化完全归之于算符的演化,这种描述方式称为Heisenberg图像 。即
A ˉ ( t ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ) ) \bar{A}(t) = (\psi(0) , \hat{A}(t) \psi(0)) A ˉ ( t ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ))
其中 A ^ ( t ) \hat{A}(t) A ^ ( t ) Heisenberg方程
d d t A ^ ( t ) = 1 i ℏ [ A ^ ( t ) , H ^ ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}(t) = \frac{1}{\mathrm{i}\hbar} [\hat{A}(t) , \hat{H}] d t d A ^ ( t ) = i ℏ 1 [ A ^ ( t ) , H ^ ]
引入时间演化算符 U ^ ( t , 0 ) = exp ( − i ℏ H ^ t ) \hat{U}(t,0) = \exp(-\frac{\mathrm{i}}{\hbar}\hat{H}t) U ^ ( t , 0 ) = exp ( − ℏ i H ^ t ) 0 0 0 t t t U ^ ( t , 0 ) ψ ( 0 ) = ψ ( t ) \hat{U}(t,0) \psi(0) = \psi(t) U ^ ( t , 0 ) ψ ( 0 ) = ψ ( t ) A ^ ( t ) \hat{A}(t) A ^ ( t )
A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e i ℏ H ^ t A ^ e − i ℏ H ^ t \hat{A}(t) = \hat{U}(t,0)^+\ \hat{A}\ \hat{U}(t,0) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \hat{A}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e ℏ i H ^ t A ^ e − ℏ i H ^ t
对于Schrödinger方程
i ℏ ∂ ∂ t ψ ( t ) = H ^ ψ ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi(t) = \hat{H} \psi(t) i ℏ ∂ t ∂ ψ ( t ) = H ^ ψ ( t )
当 H ^ \hat{H} H ^ t t t ψ ( t ) \psi(t) ψ ( t )
ψ ( t ) = U ^ ( t , 0 ) ψ ( 0 ) \psi(t) = \hat{U}(t,0) \psi(0) ψ ( t ) = U ^ ( t , 0 ) ψ ( 0 )
其中 U ^ ( t 2 , t 1 ) \hat{U}(t_2,t_1) U ^ ( t 2 , t 1 ) t 1 t_1 t 1 t 2 t_2 t 2 U ^ ( 0 , 0 ) = 1 \hat{U}(0,0) = 1 U ^ ( 0 , 0 ) = 1
i ℏ ∂ ∂ t U ^ ( t , 0 ) ψ ( 0 ) = H ^ U ^ ( t , 0 ) ψ ( 0 ) \mathrm{i}\hbar \frac{\partial}{\partial t} \hat{U}(t,0) \psi(0) = \hat{H} \hat{U}(t,0) \psi(0) i ℏ ∂ t ∂ U ^ ( t , 0 ) ψ ( 0 ) = H ^ U ^ ( t , 0 ) ψ ( 0 )
由于 ψ ( 0 ) \psi(0) ψ ( 0 )
i ℏ ∂ ∂ t U ^ ( t , 0 ) = H ^ U ^ ( t , 0 ) \mathrm{i}\hbar \frac{\partial}{\partial t} \hat{U}(t,0) = \hat{H} \hat{U}(t,0) i ℏ ∂ t ∂ U ^ ( t , 0 ) = H ^ U ^ ( t , 0 )
结合初始条件 U ^ ( 0 , 0 ) = 1 \hat{U}(0,0) = 1 U ^ ( 0 , 0 ) = 1
U ^ ( t , 0 ) = e − i ℏ H ^ t \hat{U}(t,0) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} U ^ ( t , 0 ) = e − ℏ i H ^ t
可以验证 U ^ ( t , 0 ) \hat{U}(t,0) U ^ ( t , 0 )
U ^ ( t , 0 ) + U ^ ( t , 0 ) = U ^ ( t , 0 ) U ^ ( t , 0 ) + = I \hat{U}(t,0)^+ \hat{U}(t,0) = \hat{U}(t,0) \hat{U}(t,0)^+ = I U ^ ( t , 0 ) + U ^ ( t , 0 ) = U ^ ( t , 0 ) U ^ ( t , 0 ) + = I
从而可以保证概率守恒
( ψ ( t ) , ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , ψ ( 0 ) ) (\ \psi(t) , \psi(t)\ ) = (\ \hat{U}(t,0)\psi(0) , \hat{U}(t,0)\psi(0)\ ) = (\ \psi(0) , \hat{U}(t,0)^+\hat{U}(t,0)\psi(0)\ ) = (\ \psi(0) , \psi(0)\ ) ( ψ ( t ) , ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , ψ ( 0 ) )
考虑力学量 A A A
A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ) ) \bar{A}(t) = (\ \psi(t) , \hat{A} \psi(t)\ ) \ \ \ = (\ \hat{U}(t,0)\psi(0) , \hat{A}\hat{U}(t,0)\psi(0)\ ) \ \ \ = (\ \psi(0) , \hat{U}(t,0)^+\hat{A}\hat{U}(t,0)\psi(0)\ ) \ \ \ = (\ \psi(0) , \hat{A}(t)\psi(0)\ ) A ˉ ( t ) = ( ψ ( t ) , A ^ ψ ( t ) ) = ( U ^ ( t , 0 ) ψ ( 0 ) , A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) ψ ( 0 ) ) = ( ψ ( 0 ) , A ^ ( t ) ψ ( 0 ) )
其中
A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e i ℏ H ^ t A ^ e − i ℏ H ^ t \hat{A}(t) = \hat{U}(t,0)^+\ \hat{A}\ \hat{U}(t,0) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \hat{A}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} A ^ ( t ) = U ^ ( t , 0 ) + A ^ U ^ ( t , 0 ) = e ℏ i H ^ t A ^ e − ℏ i H ^ t
考虑其随时间的变化(在下式推导中,用到了 U ^ U ^ + = I , U ^ + H ^ U ^ = H ^ , U ^ + A ^ U ^ = A ^ ( t ) \hat{U}\hat{U}^+ = I\ ,\ \hat{U}^+\hat{H}\hat{U} = \hat{H}\ ,\ \hat{U}^+\hat{A}\hat{U} = \hat{A}(t) U ^ U ^ + = I , U ^ + H ^ U ^ = H ^ , U ^ + A ^ U ^ = A ^ ( t )
d d t A ^ ( t ) = [ d d t U ^ ( t , 0 ) + ] A ^ U ^ ( t , 0 ) + U ^ ( t , 0 ) + A ^ [ d d t U ^ ( t , 0 ) ] = 1 i ℏ ( − U ^ + H ^ A ^ U ^ + U ^ + A ^ H ^ U ^ ) = 1 i ℏ ( − U ^ + H ^ U ^ U ^ + A ^ U ^ + U ^ + A ^ U ^ U ^ + H ^ U ^ ) = 1 i ℏ ( − H ^ A ^ ( t ) + A ^ ( t ) H ^ ) = 1 i ℏ [ A ^ ( t ) , H ^ ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}(t) = \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}(t,0)^+ \right] \hat{A}\ \hat{U}(t,0) + \hat{U}(t,0)^+\ \hat{A} \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}(t,0) \right] \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}^+\hat{H}\hat{A}\hat{U} + \hat{U}^+\hat{A}\hat{H}\hat{U} \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}^+\hat{H}\hat{U}\hat{U}^+\hat{A}\hat{U} + \hat{U}^+\hat{A}\hat{U}\hat{U}^+\hat{H}\hat{U} \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{H}\hat{A}(t) + \hat{A}(t)\hat{H} \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} [\hat{A}(t) , \hat{H}] d t d A ^ ( t ) = [ d t d U ^ ( t , 0 ) + ] A ^ U ^ ( t , 0 ) + U ^ ( t , 0 ) + A ^ [ d t d U ^ ( t , 0 ) ] = i ℏ 1 ( − U ^ + H ^ A ^ U ^ + U ^ + A ^ H ^ U ^ ) = i ℏ 1 ( − U ^ + H ^ U ^ U ^ + A ^ U ^ + U ^ + A ^ U ^ U ^ + H ^ U ^ ) = i ℏ 1 ( − H ^ A ^ ( t ) + A ^ ( t ) H ^ ) = i ℏ 1 [ A ^ ( t ) , H ^ ]
将Schrödinegr图像中的态与算符分别用 ψ ( S ) , A ^ ( S ) \psi^{(S)},\hat{A}^{(S)} ψ ( S ) , A ^ ( S ) ψ ( H ) , A ^ ( H ) \psi^{(H)},\hat{A}^{(H)} ψ ( H ) , A ^ ( H )
ψ ( H ) = e i ℏ H ^ t ψ ( S ) ( t ) = ψ ( S ) ( 0 ) A ^ ( H ) ( t ) = e i ℏ H ^ t A ^ ( S ) e − i ℏ H ^ t \psi^{(H)} = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \psi^{(S)}(t) = \psi^{(S)}(0) \ \ \ \hat{A}^{(H)}(t) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\ \hat{A}^{(S)}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} ψ ( H ) = e ℏ i H ^ t ψ ( S ) ( t ) = ψ ( S ) ( 0 ) A ^ ( H ) ( t ) = e ℏ i H ^ t A ^ ( S ) e − ℏ i H ^ t
在Schrödinegr图像与Heisenberg图像中守恒量算符的形式相同,如 H ^ ( S ) = H ^ ( H ) \hat{H}^{(S)} = \hat{H}^{(H)} H ^ ( S ) = H ^ ( H )
将Hamilton算符表示为两个算符之和,即
H ^ = H ^ 0 + H ^ I ( t ) \hat{H} = \hat{H}_0 + \hat{H}_I(t) H ^ = H ^ 0 + H ^ I ( t )
其中 H ^ 0 \hat{H}_0 H ^ 0 H ^ I ( t ) \hat{H}_I(t) H ^ I ( t ) U ^ 0 ( t , 0 ) = exp ( − i ℏ H ^ 0 t ) \hat{U}_0(t,0) = \exp(-\frac{\mathrm{i}}{\hbar}\hat{H}_0t) U ^ 0 ( t , 0 ) = exp ( − ℏ i H ^ 0 t )
与Schrödinger图像相比,相互作用图像中的态与算符分别表示为
ψ ( I ) ( t ) = U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = e i ℏ H ^ 0 t ψ ( S ) ( t ) A ^ ( I ) ( t ) = U ^ 0 + ( t , 0 ) A ^ ( S ) U ^ 0 ( t , 0 ) = e i ℏ H ^ 0 t A ^ ( S ) e − i ℏ H ^ 0 t \psi^{(I)}(t) = \hat{U}_0^+(t,0)\ \psi^{(S)}(t) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t}\ \psi^{(S)}(t) \ \ \ \hat{A}^{(I)}(t) = \hat{U}_0^+(t,0)\ \hat{A}^{(S)}\ \hat{U}_0(t,0) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t}\ \hat{A}^{(S)}\ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}_0t} ψ ( I ) ( t ) = U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = e ℏ i H ^ 0 t ψ ( S ) ( t ) A ^ ( I ) ( t ) = U ^ 0 + ( t , 0 ) A ^ ( S ) U ^ 0 ( t , 0 ) = e ℏ i H ^ 0 t A ^ ( S ) e − ℏ i H ^ 0 t
态 ψ ( I ) ( t ) \psi^{(I)}(t) ψ ( I ) ( t )
i ℏ ∂ ∂ t ψ ( I ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi^{(I)}(t) = \hat{H}_I^{(I)}(t) \psi^{(I)}(t) i ℏ ∂ t ∂ ψ ( I ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t )
算符 A ^ ( I ) ( t ) \hat{A}^{(I)}(t) A ^ ( I ) ( t )
d d t A ^ ( I ) ( t ) = 1 i ℏ [ A ^ ( I ) ( t ) , H ^ 0 ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}^{(I)}(t) = \frac{1}{\mathrm{i}\hbar} [\hat{A}^{(I)}(t) , \hat{H}_0] d t d A ^ ( I ) ( t ) = i ℏ 1 [ A ^ ( I ) ( t ) , H ^ 0 ]
力学量 A A A
A ˉ ( t ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) ) \bar{A}(t) = (\ \psi^{(I)}(t) , \hat{A}^{(I)}(t) \psi^{(I)}(t)\ ) A ˉ ( t ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) )
态矢 ψ ( I ) ( t ) \psi^{(I)}(t) ψ ( I ) ( t ) A ^ ( I ) ( t ) \hat{A}^{(I)}(t) A ^ ( I ) ( t )
态矢的演化由相互作用 H ^ I ( t ) \hat{H}_I(t) H ^ I ( t ) H ^ 0 \hat{H}_0 H ^ 0
相互作用图像介于Schrödinger图像和Heisenberg图像之间,在用微扰论来处理问题时有广泛的应用。
首先考虑态 ψ ( I ) ( t ) \psi^{(I)}(t) ψ ( I ) ( t )
i ℏ ∂ ∂ t ψ ( I ) ( t ) = i ℏ ∂ ∂ t [ U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) ] = ( i ℏ ∂ ∂ t e i ℏ H ^ 0 t ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ i ℏ ∂ ∂ t ψ ( S ) ( t ) ] = − ( e i ℏ H ^ 0 t H ^ 0 ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ H ^ ψ ( S ) ( t ) ] = U ^ 0 + ( t , 0 ) ( H ^ − H ^ 0 ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) U ^ 0 ( t , 0 ) U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t ) \mathrm{i}\hbar \frac{\partial}{\partial t} \psi^{(I)}(t) = \mathrm{i}\hbar \frac{\partial}{\partial t} \left[ \hat{U}_0^+(t,0)\ \psi^{(S)}(t) \right] \ \ \ = \left( \mathrm{i}\hbar \frac{\partial}{\partial t} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t} \right) \psi^{(S)}(t) + \hat{U}_0^+(t,0) \left[ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi^{(S)}(t) \right] \ \ \ = -\left( \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}_0t} \hat{H}_0 \right) \psi^{(S)}(t) + \hat{U}_0^+(t,0) \left[ \hat{H} \psi^{(S)}(t) \right] \ \ \ = \hat{U}_0^+(t,0) \left( \hat{H} - \hat{H}_0 \right) \psi^{(S)}(t) \ \ \ = \hat{U}_0^+(t,0) \hat{H}_I(t) \psi^{(S)}(t) \ \ \ = \hat{U}_0^+(t,0) \hat{H}_I(t) \hat{U}_0(t,0)\ \hat{U}_0^+(t,0) \psi^{(S)}(t) \ \ \ = \hat{H}_I^{(I)}(t) \psi^{(I)}(t) i ℏ ∂ t ∂ ψ ( I ) ( t ) = i ℏ ∂ t ∂ [ U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) ] = ( i ℏ ∂ t ∂ e ℏ i H ^ 0 t ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ i ℏ ∂ t ∂ ψ ( S ) ( t ) ] = − ( e ℏ i H ^ 0 t H ^ 0 ) ψ ( S ) ( t ) + U ^ 0 + ( t , 0 ) [ H ^ ψ ( S ) ( t ) ] = U ^ 0 + ( t , 0 ) ( H ^ − H ^ 0 ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) ψ ( S ) ( t ) = U ^ 0 + ( t , 0 ) H ^ I ( t ) U ^ 0 ( t , 0 ) U ^ 0 + ( t , 0 ) ψ ( S ) ( t ) = H ^ I ( I ) ( t ) ψ ( I ) ( t )
对于力学量算符 A ^ ( I ) ( t ) \hat{A}^{(I)}(t) A ^ ( I ) ( t )
d d t A ^ ( I ) ( t ) = [ d d t U ^ 0 ( t , 0 ) + ] A ^ U ^ 0 ( t , 0 ) + U ^ 0 ( t , 0 ) + A ^ [ d d t U ^ 0 ( t , 0 ) ] = 1 i ℏ ( − U ^ 0 + H ^ 0 A ^ U ^ 0 + U ^ 0 + A ^ H ^ 0 U ^ 0 ) = 1 i ℏ ( − U ^ 0 + H ^ 0 U ^ 0 U ^ 0 + A ^ U ^ 0 + U ^ 0 + A ^ U ^ 0 U ^ 0 + H ^ 0 U ^ 0 ) = 1 i ℏ ( − H ^ 0 A ^ ( I ) ( t ) + A ^ ( I ) ( t ) H ^ 0 ) = 1 i ℏ [ A ^ ( I ) ( t ) , H ^ 0 ] \frac{\mathrm{d}}{\mathrm{d}t} \hat{A}^{(I)}(t) = \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}_0(t,0)^+ \right] \hat{A}\ \hat{U}_0(t,0) + \hat{U}_0(t,0)^+\ \hat{A} \left[ \frac{\mathrm{d}}{\mathrm{d}t} \hat{U}_0(t,0) \right] \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}_0^+\hat{H}_0\hat{A}\hat{U}_0 + \hat{U}_0^+\hat{A}\hat{H}_0\hat{U}_0 \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{U}_0^+\hat{H}_0\hat{U}_0\hat{U}_0^+\hat{A}\hat{U}_0 + \hat{U}_0^+\hat{A}\hat{U}_0\hat{U}_0^+\hat{H}_0\hat{U}_0 \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} \left( -\hat{H}_0\hat{A}^{(I)}(t) + \hat{A}^{(I)}(t)\hat{H}_0 \right) \ \ \ = \frac{1}{\mathrm{i}\hbar} [\hat{A}^{(I)}(t) , \hat{H}_0] d t d A ^ ( I ) ( t ) = [ d t d U ^ 0 ( t , 0 ) + ] A ^ U ^ 0 ( t , 0 ) + U ^ 0 ( t , 0 ) + A ^ [ d t d U ^ 0 ( t , 0 ) ] = i ℏ 1 ( − U ^ 0 + H ^ 0 A ^ U ^ 0 + U ^ 0 + A ^ H ^ 0 U ^ 0 ) = i ℏ 1 ( − U ^ 0 + H ^ 0 U ^ 0 U ^ 0 + A ^ U ^ 0 + U ^ 0 + A ^ U ^ 0 U ^ 0 + H ^ 0 U ^ 0 ) = i ℏ 1 ( − H ^ 0 A ^ ( I ) ( t ) + A ^ ( I ) ( t ) H ^ 0 ) = i ℏ 1 [ A ^ ( I ) ( t ) , H ^ 0 ]
对于力学量 A A A
A ˉ ( t ) = ( ψ ( S ) ( t ) , A ^ ψ ( S ) ( t ) ) = ( U ^ 0 ( t , 0 ) ψ ( I ) ( t ) , A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , U ^ 0 ( t , 0 ) + A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) ) \bar{A}(t) = (\ \psi^{(S)}(t) , \hat{A} \psi^{(S)}(t)\ ) \ \ \ = (\ \hat{U}_0(t,0)\psi^{(I)}(t) , \hat{A}\hat{U}_0(t,0)\psi^{(I)}(t)\ ) \ \ \ = (\ \psi^{(I)}(t) , \hat{U}_0(t,0)^+\hat{A}\hat{U}_0(t,0)\psi^{(I)}(t)\ ) \ \ \ = (\ \psi^{(I)}(t) , \hat{A}^{(I)}(t)\psi^{(I)}(t)\ ) A ˉ ( t ) = ( ψ ( S ) ( t ) , A ^ ψ ( S ) ( t ) ) = ( U ^ 0 ( t , 0 ) ψ ( I ) ( t ) , A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , U ^ 0 ( t , 0 ) + A ^ U ^ 0 ( t , 0 ) ψ ( I ) ( t ) ) = ( ψ ( I ) ( t ) , A ^ ( I ) ( t ) ψ ( I ) ( t ) )
设体系的状态用 ψ \psi ψ ψ \psi ψ
i ℏ ∂ ∂ t ψ = H ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi = \hat{H} \psi i ℏ ∂ t ∂ ψ = H ^ ψ
考虑某种不显含 t t t Q ^ \hat{Q} Q ^
ψ ′ = Q ^ ψ \psi' = \hat{Q} \psi ψ ′ = Q ^ ψ
体系对于变换的不变性 表现为 ψ \psi ψ ψ ′ \psi' ψ ′ 相同形式的运动方程 ,即要求 ψ ′ \psi' ψ ′
i ℏ ∂ ∂ t ψ ′ = H ^ ψ ′ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi' = \hat{H} \psi' i ℏ ∂ t ∂ ψ ′ = H ^ ψ ′
即
i ℏ ∂ ∂ t Q ^ ψ = H ^ Q ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \hat{Q}\psi = \hat{H} \hat{Q}\psi i ℏ ∂ t ∂ Q ^ ψ = H ^ Q ^ ψ
两边同时用 Q ^ − 1 \hat{Q}^{-1} Q ^ − 1
i ℏ ∂ ∂ t ψ = Q ^ − 1 H ^ Q ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi = \hat{Q}^{-1}\hat{H}\hat{Q} \psi i ℏ ∂ t ∂ ψ = Q ^ − 1 H ^ Q ^ ψ
与Schrödinger方程相比较,可知 Q ^ − 1 H ^ Q ^ = H ^ \hat{Q}^{-1}\hat{H}\hat{Q} = \hat{H} Q ^ − 1 H ^ Q ^ = H ^ H ^ Q ^ = Q ^ H ^ \hat{H}\hat{Q} = \hat{Q}\hat{H} H ^ Q ^ = Q ^ H ^
[ Q ^ , H ^ ] = 0 [ \hat{Q} , \hat{H} ] = 0 [ Q ^ , H ^ ] = 0
这就是体系(Hamilton量)在变换 Q ^ \hat{Q} Q ^ 不变性 的数学表达(若 Q ^ \hat{Q} Q ^ Q Q Q 对称性变换 。
考虑到概率守恒,即 ( ψ ′ , ψ ′ ) = ( ψ , ψ ) (\psi',\psi') = (\psi,\psi) ( ψ ′ , ψ ′ ) = ( ψ , ψ )
( ψ ′ , ψ ′ ) = ( Q ^ ψ , Q ^ ψ ) = ( ψ , Q ^ + Q ^ ψ ) (\psi',\psi') = (\hat{Q}\psi,\hat{Q}\psi) = (\psi,\hat{Q}^+\hat{Q}\psi) ( ψ ′ , ψ ′ ) = ( Q ^ ψ , Q ^ ψ ) = ( ψ , Q ^ + Q ^ ψ )
故 Q ^ \hat{Q} Q ^ 幺正算符 ,即
Q ^ + Q ^ = Q ^ + Q ^ = I ^ \hat{Q}^+\hat{Q} = \hat{Q}^+\hat{Q} = \hat{I} Q ^ + Q ^ = Q ^ + Q ^ = I ^
对于连续变换,可以考虑其为连续的无穷小变换,令
Q ^ = I ^ + i ε F ^ \hat{Q} = \hat{I} + \mathrm{i}\varepsilon\hat{F} Q ^ = I ^ + i ε F ^
其中 ε → 0 + \varepsilon \to 0^+ ε → 0 + Q Q Q
Q ^ + Q ^ = ( I ^ − i ε F ^ + ) ( I ^ + i ε F ^ ) = I ^ + i ε ( F ^ − F ^ + ) + O ( ε 2 ) = I ^ \hat{Q}^+\hat{Q} = \left( \hat{I} - \mathrm{i}\varepsilon\hat{F}^+ \right) \left( \hat{I} + \mathrm{i}\varepsilon\hat{F} \right) \ \ \ = \hat{I} + \mathrm{i}\varepsilon \left( \hat{F} - \hat{F}^+ \right) + O(\varepsilon^2) = \hat{I} Q ^ + Q ^ = ( I ^ − i ε F ^ + ) ( I ^ + i ε F ^ ) = I ^ + i ε ( F ^ − F ^ + ) + O ( ε 2 ) = I ^
即要求
F ^ = F ^ + \hat{F} = \hat{F}^+ F ^ = F ^ +
则 F ^ \hat{F} F ^ 厄米算符 ,称为变换 Q ^ \hat{Q} Q ^ 无穷小算符 (infinitesimal operator),由于其为厄米算符,可用它来定义一个与 Q ^ \hat{Q} Q ^ Q ^ \hat{Q} Q ^ [ Q ^ , H ^ ] = 0 [\hat{Q},\hat{H}] = 0 [ Q ^ , H ^ ] = 0
[ F ^ , H ^ ] = 0 [ \hat{F} , \hat{H} ] = 0 [ F ^ , H ^ ] = 0
由此可知 F F F 守恒量 。
此部分仅为注解。
更普遍来讲,如果一个变换不改变体系的各物理量的相互关系,则称为体系的一个对称性变换。
设体系的某一状态用 ψ \psi ψ ψ ′ \psi' ψ ′ ϕ \phi ϕ ϕ ′ \phi' ϕ ′
∣ ( ψ , ϕ ) ∣ = ∣ ( ψ ′ , ϕ ′ ) ∣ |(\psi,\phi)| = |(\psi',\phi')| ∣ ( ψ , ϕ ) ∣ = ∣ ( ψ ′ , ϕ ′ ) ∣
基于此要求,Winger指出:对称性变换只能是幺正变换或反幺正变换。对于连续变换,它们总可以从恒等变换出发,连续地经历无穷小变换来实现,这种变换只能是幺正变换。
一个体系若存在一个守恒量,则反映体系有某种对称性,反之,不一定成立。Winger还指出:对于幺正变换对称性,的确存在相应的守恒量,但对于反幺正变换对称性,如时间反演不变性,并不存在相应的守恒量。
这里使用一维的情形进行讨论,对应的坐标算符为 x ^ \hat{x} x ^ p ^ \hat{p} p ^
空间反射算符为 P ^ \hat{P} P ^
P ^ ψ ( x ) = ψ ( − x ) \hat{P} \psi(x) = \psi(-x) P ^ ψ ( x ) = ψ ( − x )
对算符 F ^ ( x ^ , p ^ ) \hat{F}(\hat{x},\hat{p}) F ^ ( x ^ , p ^ )
P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ ) \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ = \hat{F}(-\hat{x},-\hat{p}) P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ )
证明如下:
设算符 F ^ ( x ^ , p ^ ) \hat{F}(\hat{x},\hat{p}) F ^ ( x ^ , p ^ ) ψ ( x ) \psi(x) ψ ( x )
F ^ ( x ^ , p ^ ) ψ ( x ) = ϕ ( x ) \hat{F}(\hat{x},\hat{p}) \psi(x) = \phi(x) F ^ ( x ^ , p ^ ) ψ ( x ) = ϕ ( x )
做空间反射变换可得
P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ ϕ ( x ) \hat{P} \hat{F}(\hat{x},\hat{p}) \psi(x) = \hat{P} \phi(x) P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ ϕ ( x )
其中
P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = F ^ ( − x ^ , − p ^ ) ψ ( − x ) \hat{P} \hat{F}(\hat{x},\hat{p}) \psi(x) = \hat{F}(-\hat{x},-\hat{p}) \psi(-x) P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = F ^ ( − x ^ , − p ^ ) ψ ( − x )
已知 P ^ \hat{P} P ^
P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + P ^ ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + ψ ( − x ) \hat{P} \hat{F}(\hat{x},\hat{p}) \psi(x) = \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ \hat{P} \psi(x) = \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ \psi(-x) P ^ F ^ ( x ^ , p ^ ) ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + P ^ ψ ( x ) = P ^ F ^ ( x ^ , p ^ ) P ^ + ψ ( − x )
两者对比有
P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ ) \hat{P} \hat{F}(\hat{x},\hat{p}) \hat{P}^+ = \hat{F}(-\hat{x},-\hat{p}) P ^ F ^ ( x ^ , p ^ ) P ^ + = F ^ ( − x ^ , − p ^ )
如果Hamilton量空间反射不变,即
[ P ^ , H ^ ] = 0 [ \hat{P} , \hat{H} ] = 0 [ P ^ , H ^ ] = 0
则体系具有空间反射对称性 ,此时体系的宇称守恒 。
这里使用一维的情形进行讨论,对应的坐标算符为 x ^ \hat{x} x ^ p ^ \hat{p} p ^
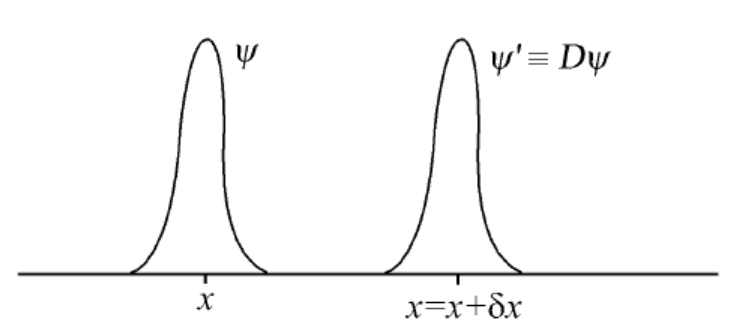
考虑体系沿 x x x x → x ′ = x + δ x x \to x' = x + \delta x x → x ′ = x + δ x ψ \psi ψ
ψ ′ = D ^ ( δ x ) ψ \psi' = \hat{D}(\delta x) \psi ψ ′ = D ^ ( δ x ) ψ
无穷小平移变换 D ^ ( δ x ) \hat{D}(\delta x) D ^ ( δ x ) D ^ + ( δ x ) = D ^ − 1 ( δ x ) \hat{D}^+(\delta x) = \hat{D}^{-1}(\delta x) D ^ + ( δ x ) = D ^ − 1 ( δ x ) p ^ \hat{p} p ^
D ^ ( δ x ) = e − i ℏ δ x p ^ \hat{D}(\delta x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} D ^ ( δ x ) = e − ℏ i δ x p ^
证明如下:
对任意态 ψ \psi ψ ψ ′ \psi' ψ ′ x x x
∫ − ∞ + ∞ ψ ′ ∗ ( x ) x ψ ′ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x ) x ψ ( x ) d x + δ x = ∫ − ∞ + ∞ ψ ∗ ( x ) ( x + δ x ) ψ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x − δ x ) x ψ ( x − δ x ) d x \int_{-\infty}^{+\infty} \psi'^(x) x \psi'(x) \mathrm{d}x = \int_{-\infty}^{+\infty} \psi^ (x) x \psi(x) \mathrm{d}x + \delta x \ \ \ = \int_{-\infty}^{+\infty} \psi^(x) (x+\delta x) \psi(x) \mathrm{d}x \ \ \ = \int_{-\infty}^{+\infty} \psi^ (x-\delta x) x \psi(x-\delta x) \mathrm{d}x ∫ − ∞ + ∞ ψ ′ ∗ ( x ) x ψ ′ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x ) x ψ ( x ) d x + δ x = ∫ − ∞ + ∞ ψ ∗ ( x ) ( x + δ x ) ψ ( x ) d x = ∫ − ∞ + ∞ ψ ∗ ( x − δ x ) x ψ ( x − δ x ) d x
由此可知
ψ ′ ( x ) = ψ ( x − δ x ) \psi'(x) = \psi(x-\delta x) ψ ′ ( x ) = ψ ( x − δ x )
即 D ^ ( δ x ) ψ ( x ) = ψ ( x − δ x ) \hat{D}(\delta x) \psi(x) = \psi(x-\delta x) D ^ ( δ x ) ψ ( x ) = ψ ( x − δ x ) x x x
D ^ ( δ x ) ψ ( x ) = ∑ n = 0 + ∞ ( − δ x ) n n ! ∂ n ψ ( x ) ∂ x n = e − δ x ∂ ∂ x ψ ( x ) \hat{D}(\delta x) \psi(x) = \sum_{n=0}^{+\infty} \frac{(-\delta x)^n}{n!} \frac{\partial^n \psi(x)}{\partial x^n} = \mathrm{e}^{-\delta x \frac{\partial}{\partial x}} \psi(x) D ^ ( δ x ) ψ ( x ) = n = 0 ∑ + ∞ n ! ( − δ x ) n ∂ x n ∂ n ψ ( x ) = e − δ x ∂ x ∂ ψ ( x )
因为 ψ ( x ) \psi(x) ψ ( x ) p ^ = − i ℏ ∂ ∂ x \hat{p} = -\mathrm{i}\hbar \frac{\partial}{\partial x} p ^ = − i ℏ ∂ x ∂
D ^ ( δ x ) = e − i ℏ δ x p ^ \hat{D}(\delta x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} D ^ ( δ x ) = e − ℏ i δ x p ^
取厄米共轭可得
D ^ + ( δ x ) = ( e − i ℏ δ x p ^ ) + = [ ∑ n = 0 + ∞ 1 n ! ( − i ℏ δ x ) n p ^ n ] + = ∑ n = 0 + ∞ 1 n ! ( i ℏ δ x ) n p ^ n = e i ℏ δ x p ^ = D ^ − 1 ( δ x ) \hat{D}^+(\delta x) = \left( \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} \right)^+ \ \ \ = \left[ \sum_{n=0}^{+\infty} \frac{1}{n!} ( -\frac{\mathrm{i}}{\hbar}\delta x )^n \hat{p}^n \right]^+ \ \ \ = \sum_{n=0}^{+\infty} \frac{1}{n!} ( \frac{\mathrm{i}}{\hbar}\delta x )^n \hat{p}^n \ \ \ = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} \ \ \ = \hat{D}^{-1}(\delta x) D ^ + ( δ x ) = ( e − ℏ i δ x p ^ ) + = [ n = 0 ∑ + ∞ n ! 1 ( − ℏ i δ x ) n p ^ n ] + = n = 0 ∑ + ∞ n ! 1 ( ℏ i δ x ) n p ^ n = e ℏ i δ x p ^ = D ^ − 1 ( δ x )
即 D ^ ( δ x ) \hat{D}(\delta x) D ^ ( δ x )
D ^ ( δ x ) ψ ( x ) = e − i ℏ δ x p ^ ψ ( x ) = ψ ( x − δ x ) \hat{D}(\delta x) \psi(x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}}\psi(x) = \psi(x-\delta x) D ^ ( δ x ) ψ ( x ) = e − ℏ i δ x p ^ ψ ( x ) = ψ ( x − δ x )
D ^ ( δ x ) F ^ D ^ + ( δ x ) = e − i ℏ δ x p ^ F ^ e i ℏ δ x p ^ \hat{D}(\delta x)\hat{F}\hat{D}^+(\delta x) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} \hat{F} \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\delta x \hat{p}} D ^ ( δ x ) F ^ D ^ + ( δ x ) = e − ℏ i δ x p ^ F ^ e ℏ i δ x p ^
如果Hamilton量空间平移不变,即
[ D ^ , H ^ ] = 0 [ \hat{D} , \hat{H} ] = 0 [ D ^ , H ^ ] = 0
则体系具有空间平移对称性 ,此时体系的动量守恒 。
这是因为
[ D ^ , H ^ ] = 0 ⇓ [ ∑ n = 0 + ∞ 1 n ! ( − i ℏ δ x ) n p ^ n , H ^ ] = 0 ⇓ ∑ n = 0 + ∞ 1 n ! ( − i ℏ δ x ) n [ p ^ n , H ^ ] = 0 ⇓ [ p ^ , H ^ ] = 0 \ [ \hat{D} , \hat{H} ] = 0 \ \Downarrow \ \ [ \sum_{n=0}^{+\infty} \frac{1}{n!} ( -\frac{\mathrm{i}}{\hbar}\delta x )^n \hat{p}^n , \hat{H} ] = 0 \ \Downarrow \ \ \sum_{n=0}^{+\infty} \frac{1}{n!} ( -\frac{\mathrm{i}}{\hbar}\delta x )^n [ \hat{p}^n , \hat{H} ] = 0 \ \Downarrow \ \ [ \hat{p} , \hat{H} ] = 0 [ D ^ , H ^ ] = 0 ⇓ [ n = 0 ∑ + ∞ n ! 1 ( − ℏ i δ x ) n p ^ n , H ^ ] = 0 ⇓ n = 0 ∑ + ∞ n ! 1 ( − ℏ i δ x ) n [ p ^ n , H ^ ] = 0 ⇓ [ p ^ , H ^ ] = 0
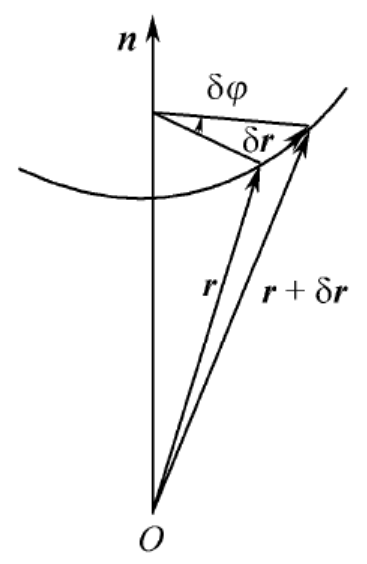
考虑体系绕 n ⃗ \vec{n}, n φ → φ ′ = φ + δ φ \varphi \to \varphi' = \varphi + \delta \varphi φ → φ ′ = φ + δ φ ψ \psi ψ
ψ ′ = R ^ ( δ φ n ⃗ ) ψ \psi' = \hat{R}(\delta \varphi\ \vec{n}) \psi ψ ′ = R ^ ( δ φ n ) ψ
无穷小转动变换 R ^ ( δ φ n ⃗ ) \hat{R}(\delta \varphi\ \vec{n}) R ^ ( δ φ n ) R ^ + ( δ φ n ⃗ ) = R ^ − 1 ( δ φ n ⃗ ) \hat{R}^+(\delta \varphi\ \vec{n}) = \hat{R}^{-1}(\delta \varphi\ \vec{n}) R ^ + ( δ φ n ) = R ^ − 1 ( δ φ n ) L ^ \hat{L} L ^
R ^ ( δ φ n ⃗ ) = e − i ℏ δ φ n ⃗ ⋅ L ⃗ ^ \hat{R}(\delta \varphi\ \vec{n}) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi\ \vec{n} \cdot \hat{\vec{L}}} R ^ ( δ φ n ) = e − ℏ i δ φ n ⋅ L ^
如果 n ⃗ \vec{n}, n z z z
R ^ ( δ φ ) = e − i ℏ δ φ L ^ z \hat{R}(\delta \varphi) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} R ^ ( δ φ ) = e − ℏ i δ φ L ^ z
以 n ⃗ \vec{n}, n z z z
R ^ ( δ φ ) ψ ( φ ) = e − i ℏ δ φ L ^ z ψ ( φ ) = ψ ( φ − δ φ ) \hat{R}(\delta \varphi) \psi(\varphi) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} \psi(\varphi) = \psi(\varphi-\delta \varphi) R ^ ( δ φ ) ψ ( φ ) = e − ℏ i δ φ L ^ z ψ ( φ ) = ψ ( φ − δ φ )
R ^ ( δ φ ) F ^ ( φ ) R ^ + ( δ φ ) = e − i ℏ δ φ L ^ z F ^ ( φ ) e i ℏ δ φ L ^ z \hat{R}(\delta \varphi) \hat{F}(\varphi) \hat{R}^+(\delta \varphi) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} \hat{F}(\varphi) \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\delta \varphi \hat{L}_z} R ^ ( δ φ ) F ^ ( φ ) R ^ + ( δ φ ) = e − ℏ i δ φ L ^ z F ^ ( φ ) e ℏ i δ φ L ^ z
如果Hamilton量空间转动不变,即
[ R ^ , H ^ ] = 0 [ \hat{R} , \hat{H} ] = 0 [ R ^ , H ^ ] = 0
则体系具有空间转动对称性 ,此时体系的角动量守恒 ,即
[ L ⃗ ^ , H ^ ] = 0 [ \hat{\vec{L}} , \hat{H} ] = 0 [ L ^ , H ^ ] = 0
考虑将时间停滞一段 τ \tau τ
D ^ ( τ ) ψ ( t ) = ψ ( t + τ ) \hat{D}(\tau) \psi(t) = \psi(t+\tau) D ^ ( τ ) ψ ( t ) = ψ ( t + τ )
这称为时间平移变换 (属于连续变换),算符
D ^ ( τ ) = e τ ∂ ∂ t \hat{D}(\tau) = \mathrm{e}^{\tau \frac{\partial}{\partial t}} D ^ ( τ ) = e τ ∂ t ∂
如果Hamilton量时间平移不变,即
D ^ ( τ ) H ^ D ^ + ( τ ) = H ^ \hat{D}(\tau) \hat{H} \hat{D}^+(\tau) = \hat{H} D ^ ( τ ) H ^ D ^ + ( τ ) = H ^
此即 [ D ^ ( τ ) , H ^ ] = 0 [\hat{D}(\tau) , \hat{H}] = 0 [ D ^ ( τ ) , H ^ ] = 0 能量守恒 。证明如下:
[ D ^ ( τ ) , H ^ ] = 0 ⇓ [ e τ ∂ ∂ t , H ^ ] = 0 ⇓ [ ∑ n = 0 + ∞ τ n n ! ∂ n ∂ t n , H ^ ] = 0 ⇓ ∑ n = 0 + ∞ τ n n ! [ ∂ n ∂ t n , H ^ ] = 0 ⇓ [ ∂ ∂ t , H ^ ] = 0 ⇓ [ ∂ ∂ t , H ^ ] ψ = ∂ ∂ t ( H ^ ψ ) − H ^ ∂ ∂ t ψ = ψ ∂ H ^ ∂ t = 0 ⇓ ∂ H ^ ∂ t = 0 \left[ \hat{D}(\tau) , \hat{H} \right] = 0 \ \Downarrow \ \left[ \mathrm{e}^{\tau \frac{\partial}{\partial t}} , \hat{H} \right] = 0 \ \Downarrow \ \left[ \sum_{n=0}^{+\infty} \frac{\tau^n}{n!} \frac{\partial^n}{\partial t^n} , \hat{H} \right] = 0 \ \Downarrow \ \sum_{n=0}^{+\infty} \frac{\tau^n}{n!} \left[ \frac{\partial^n}{\partial t^n} , \hat{H} \right] = 0 \ \Downarrow \ \left[ \frac{\partial}{\partial t} , \hat{H} \right] = 0 \ \Downarrow \ \left[ \frac{\partial}{\partial t} , \hat{H} \right] \psi = \frac{\partial}{\partial t} (\hat{H} \psi) - \hat{H} \frac{\partial}{\partial t} \psi = \psi \frac{\partial \hat{H}}{\partial t} = 0 \ \Downarrow \ \frac{\partial \hat{H}}{\partial t} = 0 [ D ^ ( τ ) , H ^ ] = 0 ⇓ [ e τ ∂ t ∂ , H ^ ] = 0 ⇓ [ n = 0 ∑ + ∞ n ! τ n ∂ t n ∂ n , H ^ ] = 0 ⇓ n = 0 ∑ + ∞ n ! τ n [ ∂ t n ∂ n , H ^ ] = 0 ⇓ [ ∂ t ∂ , H ^ ] = 0 ⇓ [ ∂ t ∂ , H ^ ] ψ = ∂ t ∂ ( H ^ ψ ) − H ^ ∂ t ∂ ψ = ψ ∂ t ∂ H ^ = 0 ⇓ ∂ t ∂ H ^ = 0
此时可以证明时间平移变换可以表示为
D ^ ( τ ) = e − i ℏ τ H ^ \hat{D}(\tau) = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \tau \hat{H}} D ^ ( τ ) = e − ℏ i τ H ^
即与时间平移变换相联系的力学量是能量。证明如下
根据Schrödinger方程
i ℏ ∂ ∂ t ψ = H ^ ψ \mathrm{i}\hbar \frac{\partial}{\partial t} \psi = \hat{H} \psi i ℏ ∂ t ∂ ψ = H ^ ψ
可知
∂ ∂ t ψ = 1 i ℏ H ^ ψ \frac{\partial}{\partial t} \psi = \frac{1}{\mathrm{i}\hbar} \hat{H} \psi ∂ t ∂ ψ = i ℏ 1 H ^ ψ
归纳可得
∂ n ∂ t n ψ = ( 1 i ℏ H ^ ) n ψ \frac{\partial^n}{\partial t^n} \psi = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^n \psi ∂ t n ∂ n ψ = ( i ℏ 1 H ^ ) n ψ
这是因为在已知对 n − 1 n-1 n − 1
∂ n ∂ t n ψ = ∂ ∂ t [ ( 1 i ℏ H ^ ) n − 1 ψ ] = ( 1 i ℏ H ^ ) n − 1 ∂ ψ ∂ t + ψ ∂ ∂ t ( 1 i ℏ H ^ ) n − 1 = ( 1 i ℏ H ^ ) n − 1 1 i ℏ H ^ ψ + ψ ( 1 i ℏ ) n − 1 ( n − 1 ) H ^ n − 2 ∂ H ^ ∂ t = ( 1 i ℏ H ^ ) n ψ \frac{\partial^n}{\partial t^n} \psi = \frac{\partial}{\partial t} \left[ \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \psi \right] \ \ \ = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \frac{\partial \psi}{\partial t} + \psi \frac{\partial}{\partial t} \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \ \ \ = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^{n-1} \frac{1}{\mathrm{i}\hbar} \hat{H} \psi + \psi \left( \frac{1}{\mathrm{i}\hbar}\right)^{n-1} (n-1) \hat{H}^{n-2} \frac{\partial \hat{H}}{\partial t} \ \ \ = \left( \frac{1}{\mathrm{i}\hbar} \hat{H} \right)^n \psi ∂ t n ∂ n ψ = ∂ t ∂ [ ( i ℏ 1 H ^ ) n − 1 ψ ] = ( i ℏ 1 H ^ ) n − 1 ∂ t ∂ ψ + ψ ∂ t ∂ ( i ℏ 1 H ^ ) n − 1 = ( i ℏ 1 H ^ ) n − 1 i ℏ 1 H ^ ψ + ψ ( i ℏ 1 ) n − 1 ( n − 1 ) H ^ n − 2 ∂ t ∂ H ^ = ( i ℏ 1 H ^ ) n ψ
在量子力学中,把属于同一类的粒子成为全同 (identical)粒子 ,它们具有完全相同的内禀属性,包括静质量、电荷、自旋、磁矩、寿命等。
量子力学中,由于态的量子化 ,两个量子态要么完全相同,要么完全不同,中间无连续过度,因此与经典力学的连续变化不同,具有全同粒子的问题。
当两个全同粒子的波函数在空间中发生重叠的时候,我们无法区分哪个是“第一个”粒子,哪个是“第二个”粒子。所以全同粒子是不可分辨 的,即不能“标记”、“跟踪”,此时经典统计被量子统计取代。
全部量子力学实验表明,如果让两个全同粒子处于相同的物理条件下,它们将有完全相同的实验表现,故从原理上 (永远的、非技术性的)看将无法区分它们谁是谁。
全同粒子体系中任意两个全同粒子的交换,都不改变体系的物理状态,即所处的量子态是不变的,故可观测量(尤其是Hamilton量)是不变的。
考虑 N N N ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) q i ( i = 1 , 2 , ⋯ , N ) q_i\ (i=1,2,\cdots,N) q i ( i = 1 , 2 , ⋯ , N ) 交换算符 P ^ i j \hat{P}_{ij} P ^ ij i i i j j j
P ^ i j ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) = ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) \hat{P}_{ij} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) = \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) P ^ ij ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) = ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N )
而根据全同性假设, ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N )
P ^ i j ψ = C ψ ⇓ P ^ i j 2 ψ = C 2 ψ = ψ ⇓ C 2 = 1 ⇓ C = ± 1 \hat{P}{ij} \psi = C \psi \ \Downarrow \ \hat{P} {ij}^2 \psi = C^2 \psi = \psi \ \Downarrow \ C^2 = 1 \ \Downarrow \ C = \pm 1 P ^ ij ψ = C ψ ⇓ P ^ ij 2 ψ = C 2 ψ = ψ ⇓ C 2 = 1 ⇓ C = ± 1
即 P ^ i j \hat{P}_{ij} P ^ ij C = ± 1 C = \pm 1 C = ± 1
P ^ i j ψ = { + ψ , 交换对称波函数 − ψ , 交换反对称波函数 \hat{P}_{ij} \psi = \begin{cases} + \psi & ,交换对称波函数 \ - \psi & ,交换反对称波函数 \ \end{cases} P ^ ij ψ = { + ψ − ψ , 交换对称波函数 , 交换反对称波函数
所以全同粒子体系的全同性假设给了波函数一个很强的限制,即要求它们对于任意两个粒子交换,或者对称 (symmetric),或者反对称 (anti-symmetrix)。
注:交换算符是厄米算符、幺正算符,这是因为:
∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) P ^ i j ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) d τ = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ( 令 d τ ′ = d q 1 ⋯ d q j ⋯ d q i ⋯ d q N = d τ ) = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ = ∫ ( 全 ) [ P ^ i j ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) ] ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ ⇓ P ^ i j + = P ^ i j \int_{(全)} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \hat{P}{ij} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \mathrm{d}\tau \ \ \ = \int {(全)} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \mathrm{d}\tau \ \ \ (令 \mathrm{d}\tau' = \mathrm{d}q_1\cdots\mathrm{d}q_j\cdots\mathrm{d}q_i\cdots\mathrm{d}q_N = \mathrm{d}\tau) \ \ \ = \int_{(全)} \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \mathrm{d}\tau' \ \ \ = \int_{(全)} \left[ \hat{P}{ij}\psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \right] \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) \mathrm{d}\tau' \ \Downarrow \ \hat{P} {ij}^+ = \hat{P}_{ij} ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) P ^ ij ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) d τ = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ( 令 d τ ′ = d q 1 ⋯ d q j ⋯ d q i ⋯ d q N = d τ ) = ∫ ( 全 ) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ = ∫ ( 全 ) [ P ^ ij ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) ] ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) d τ ′ ⇓ P ^ ij + = P ^ ij
P ^ i j P ^ i j = I ^ ⟹ P ^ i j = P ^ i j − 1 ⟹ P ^ i j + = P ^ i j − 1 \hat{P}{ij}\hat{P} {ij} = \hat{I} \Longrightarrow \hat{P}{ij} = \hat{P} {ij}^{-1} \Longrightarrow \hat{P}{ij}^+ = \hat{P} {ij}^{-1} P ^ ij P ^ ij = I ^ ⟹ P ^ ij = P ^ ij − 1 ⟹ P ^ ij + = P ^ ij − 1
对于全同粒子体系,
[ P ^ i j , H ^ ] = 0 ( i ≠ j = 1 , 2 , 3 , ⋯ , N ) [\hat{P}_{ij} , \hat{H}] = 0 \kern 2em (i \ne j = 1,2,3,\cdots,N) [ P ^ ij , H ^ ] = 0 ( i = j = 1 , 2 , 3 , ⋯ , N )
即所有的 P ^ i j \hat{P}_{ij} P ^ ij
P ^ i j H ^ P ^ i j + = H ^ \hat{P}{ij} \hat{H} \hat{P} {ij}^+ = \hat{H} P ^ ij H ^ P ^ ij + = H ^
证明如下:
记 ( q i , q j ) = ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) (q_i,q_j) = (q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ( q i , q j ) = ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N )
H ^ ( q i , q j ) ψ ( q i , q j ) = E ψ ( q i , q j ) \hat{H} (q_i,q_j) \psi(q_i,q_j) = E \psi(q_i,q_j) H ^ ( q i , q j ) ψ ( q i , q j ) = E ψ ( q i , q j )
两边同时用 P ^ i j \hat{P}_{ij} P ^ ij
P ^ i j [ H ^ ( q i , q j ) ψ ( q i , q j ) ] = P ^ i j [ E ψ ( q i , q j ) ] ⇓ H ^ ( q j , q i ) ψ ( q j , q i ) = E ψ ( q j , q i ) \hat{P}{ij} \left[ \hat{H} (q_i,q_j) \psi(q_i,q_j) \right] = \hat{P} {ij} \left[ E \psi(q_i,q_j) \right] \ \Downarrow \ \hat{H} (q_j,q_i) \psi(q_j,q_i) = E \psi(q_j,q_i) P ^ ij [ H ^ ( q i , q j ) ψ ( q i , q j ) ] = P ^ ij [ E ψ ( q i , q j ) ] ⇓ H ^ ( q j , q i ) ψ ( q j , q i ) = E ψ ( q j , q i )
考虑到波函数的交换对称性,即 ψ ( q j , q i ) = C ψ ( q i , q j ) \psi(q_j,q_i) = C \psi(q_i,q_j) ψ ( q j , q i ) = C ψ ( q i , q j )
H ^ ( q j , q i ) C ψ ( q i , q j ) = E C ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) ψ ( q i , q j ) = E ψ ( q i , q j ) = H ^ ( q i , q j ) ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) = H ^ ( q i , q j ) ⇓ P ^ i j H ^ ( q i , q j ) P ^ i j + = H ^ ( q i , q j ) ⇓ [ P ^ i j , H ^ ] = 0 \hat{H} (q_j,q_i) C \psi(q_i,q_j) = E C \psi(q_i,q_j) \ \Downarrow \ \hat{H} (q_j,q_i) \psi(q_i,q_j) = E \psi(q_i,q_j) = \hat{H} (q_i,q_j) \psi(q_i,q_j) \ \Downarrow \ \hat{H} (q_j,q_i) = \hat{H} (q_i,q_j) \ \Downarrow \ \hat{P}{ij} \hat{H} (q_i,q_j) \hat{P} {ij}^+ = \hat{H} (q_i,q_j) \ \Downarrow \ \ [\hat{P}_{ij} , \hat{H}] = 0 H ^ ( q j , q i ) C ψ ( q i , q j ) = EC ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) ψ ( q i , q j ) = E ψ ( q i , q j ) = H ^ ( q i , q j ) ψ ( q i , q j ) ⇓ H ^ ( q j , q i ) = H ^ ( q i , q j ) ⇓ P ^ ij H ^ ( q i , q j ) P ^ ij + = H ^ ( q i , q j ) ⇓ [ P ^ ij , H ^ ] = 0
凡自旋为 ℏ \hbar ℏ 整数倍 ( s = 0 , 1 , 2 , ⋯ ) (s=0,1,2,\cdots) ( s = 0 , 1 , 2 , ⋯ ) 对称 的,如 π \pi π ( s = 0 ) (s=0) ( s = 0 ) ( s = 1 ) (s=1) ( s = 1 ) Bose-Einstein统计 ,故称为Bose子 。
凡自旋为 ℏ \hbar ℏ 半整数倍 ( s = 1 2 , 3 2 , ⋯ ) (s=\frac12,\frac32,\cdots) ( s = 2 1 , 2 3 , ⋯ ) 反对称 的,如电子、质子、中子 ( 均 s = 1 2 ) (均s=\frac12) ( 均 s = 2 1 ) Fermi-Dirac统计 ,故称为Fermi子 。
由基本粒子所组成的复合粒子,若在讨论的问题或过程中其内部状态保持不变,即内部自由度完全被冻结,则全同性概念仍然使用,也可以当成一类全同粒子来处理,其统计性质按如下规则确定:
若复合粒子由Bose子组成,则为Bose子;
若复合粒子由偶数个Fermi子组成,则为Bose子;
若复合粒子由奇数个Fermi子组成,则为Fermi子。
若 ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) \psi(q_1,\cdots,q_i,\cdots,q_j,\cdots,q_N) ψ ( q 1 , ⋯ , q i , ⋯ , q j , ⋯ , q N ) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N ) \psi(q_1,\cdots,q_j,\cdots,q_i,\cdots,q_N) ψ ( q 1 , ⋯ , q j , ⋯ , q i , ⋯ , q N )
由上述定理可得:把全同粒子体系的波函数和其交换项进行叠加,叠加后的波函数仍满足Schrödinger方程, 这是我们能够将波函数对称化或反对称化的理论依据。
一般地说,一个全同粒子体系的波函数是解Schrödinger方程得到的,但未必有确定的交换对称性,而交换算符与Hamilton量的共同本征函数是完全对称波函数或完全反对称波函数,所以我们要对解得的波函数进行“对称化 ”或“反对称化 ”。
忽略全同粒子体系中各粒子之间的相互作用,可以将其视为无耦合体系,此时体系的总波函数是各个粒子波函数的乘积,Hamilton量是各个粒子Hamilton量的和
Ψ ( q 1 , q 2 ⋯ , q N ) = ψ 1 ( q 1 ) ψ 2 ( q 2 ) ⋯ ψ N ( q N ) \Psi(q_1,q_2\cdots,q_N) = \psi_1(q_1) \psi_2(q_2) \cdots \psi_N(q_N) Ψ ( q 1 , q 2 ⋯ , q N ) = ψ 1 ( q 1 ) ψ 2 ( q 2 ) ⋯ ψ N ( q N )
H ^ = ∑ i H ^ i \hat{H} = \sum_i \hat{H}_i H ^ = i ∑ H ^ i
二粒子体系进行单粒子近似后得到的波函数为
Ψ ( q 1 , q 2 ) = ψ 1 ( q 1 ) ψ 2 ( q 2 ) \Psi(q_1,q_2) = \psi_1(q_1) \psi_2(q_2) Ψ ( q 1 , q 2 ) = ψ 1 ( q 1 ) ψ 2 ( q 2 )
进行对称化 后,归一化的波函数为
Ψ S ( q 1 , q 2 ) = 1 2 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) + ψ 1 ( q 2 ) ψ 2 ( q 1 ) ] \Psi^S(q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_1(q_1)\psi_2(q_2) + \psi_1(q_2)\psi_2(q_1) \right] Ψ S ( q 1 , q 2 ) = 2 1 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) + ψ 1 ( q 2 ) ψ 2 ( q 1 ) ]
进行反对称化 后,归一化的波函数为
Ψ A ( q 1 , q 2 ) = 1 2 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) − ψ 1 ( q 2 ) ψ 2 ( q 1 ) ] \Psi^A(q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_1(q_1)\psi_2(q_2) - \psi_1(q_2)\psi_2(q_1) \right] Ψ A ( q 1 , q 2 ) = 2 1 [ ψ 1 ( q 1 ) ψ 2 ( q 2 ) − ψ 1 ( q 2 ) ψ 2 ( q 1 ) ]
对于两个全同Bose子 组成的体系,应该满足交换对称 ,即
P ^ 12 Ψ k 1 k 2 S ( q 1 , q 2 ) = Ψ k 1 k 2 S ( q 1 , q 2 ) \hat{P}{12} \Psi^S {k_1k_2} (q_1,q_2) = \Psi^S_{k_1k_2} (q_1,q_2) P ^ 12 Ψ k 1 k 2 S ( q 1 , q 2 ) = Ψ k 1 k 2 S ( q 1 , q 2 )
当 k 1 ≠ k 2 k_1 \ne k_2 k 1 = k 2
Ψ k 1 k 2 S ( q 1 , q 2 ) = 1 2 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) + ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 1 2 ( 1 + P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) \Psi^S_{k_1k_2} (q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_{k_1}(q_1)\psi_{k_2}(q_2) + \psi_{k_1}(q_2)\psi_{k_2}(q_1) \right] \ \ \ = \frac{1}{\sqrt{2}} \left( 1 + \hat{P}{12} \right) \psi {k_1}(q_1)\psi_{k_2}(q_2) Ψ k 1 k 2 S ( q 1 , q 2 ) = 2 1 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) + ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 2 1 ( 1 + P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 )
当 k 1 = k 2 = k k_1 = k_2 = k k 1 = k 2 = k
Ψ k k S ( q 1 , q 2 ) = ψ k ( q 1 ) ψ k ( q 2 ) \Psi^S_{kk} (q_1,q_2) = \psi_{k}(q_1)\psi_{k}(q_2) Ψ kk S ( q 1 , q 2 ) = ψ k ( q 1 ) ψ k ( q 2 )
该波函数不恒为零表明在一个粒子态上可以存在多个Bose子。
对于两个全同Fermi子 组成的体系,应该满足交换反对称 ,即
P ^ 12 Ψ k 1 k 2 A ( q 1 , q 2 ) = − Ψ k 1 k 2 A ( q 1 , q 2 ) \hat{P}{12} \Psi^A {k_1k_2} (q_1,q_2) = - \Psi^A_{k_1k_2} (q_1,q_2) P ^ 12 Ψ k 1 k 2 A ( q 1 , q 2 ) = − Ψ k 1 k 2 A ( q 1 , q 2 )
当 k 1 ≠ k 2 k_1 \ne k_2 k 1 = k 2
Ψ k 1 k 2 A ( q 1 , q 2 ) = 1 2 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) − ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 1 2 ∣ ψ k 1 ( q 1 ) ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ψ k 2 ( q 2 ) ∣ = 1 2 ( 1 − P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) \Psi^A_{k_1k_2} (q_1,q_2) = \frac{1}{\sqrt{2}} \left[ \psi_{k_1}(q_1)\psi_{k_2}(q_2) - \psi_{k_1}(q_2)\psi_{k_2}(q_1) \right] \ \ \ = \frac{1}{\sqrt{2}} \begin{vmatrix} \psi_{k_1}(q_1) & \psi_{k_1}(q_2) \ \psi_{k_2}(q_1) & \psi_{k_2}(q_2) \end{vmatrix} \ \ \ = \frac{1}{\sqrt{2}} \left( 1 - \hat{P}{12} \right) \psi {k_1}(q_1)\psi_{k_2}(q_2) Ψ k 1 k 2 A ( q 1 , q 2 ) = 2 1 [ ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) − ψ k 1 ( q 2 ) ψ k 2 ( q 1 ) ] = 2 1 ψ k 1 ( q 1 ) ψ k 2 ( q 1 ) ψ k 1 ( q 2 ) ψ k 2 ( q 2 ) = 2 1 ( 1 − P ^ 12 ) ψ k 1 ( q 1 ) ψ k 2 ( q 2 )
当 k 1 = k 2 = k k_1 = k_2 = k k 1 = k 2 = k Ψ k k A ( q 1 q 2 ) ≡ 0 \Psi^A_{kk}(q_1q_2) \equiv 0 Ψ kk A ( q 1 q 2 ) ≡ 0 Pauli不相容原理 。
由于Bose子不受Pauli不相容原理的限制,可以有多个Bose子处在同一量子态上,故设有 N N N M M M M ≤ N M \le N M ≤ N n i n_i n i k i k_i k i i = 0 , 1 , ⋯ , M i=0,1,\cdots,M i = 0 , 1 , ⋯ , M ∑ i = 1 M n i = N \sum_{i=1}^{M} n_i = N ∑ i = 1 M n i = N
Ψ k 1 ⋯ k M S ( q 1 , ⋯ , q N ) = ∏ i = 1 M n i ! N ! ∑ P ^ P ^ ∏ i = 1 M ∏ j = 1 n i ψ k i ( q N i − 1 + j ) \Psi^{S}{k_1 \cdots k_M} (q_1,\cdots,q_N) = \sqrt{\frac{\prod {i=1}^{M}n_i!}{N!}} \sum_{\hat{P}} \hat{P} \prod_{i=1}^{M} \prod_{j=1}^{n_i} \psi_{k_i}(q_{N_{i-1}+j}) Ψ k 1 ⋯ k M S ( q 1 , ⋯ , q N ) = N ! ∏ i = 1 M n i ! P ^ ∑ P ^ i = 1 ∏ M j = 1 ∏ n i ψ k i ( q N i − 1 + j )
式中 Ψ S \Psi^S Ψ S k i k_i k i n i n_i n i N i = ∑ l = 1 i n l N_i = \sum_{l=1}^{i} n_l N i = ∑ l = 1 i n l i i i P ^ \hat{P} P ^ 这样其个数就与组合数而非排列数相关 ),这样的置换共有
∏ i = 1 M C N i n i = ∏ i = 1 M N i ! ( N i − n i ) ! n i ! = ∏ i = 1 M N i ! N i − 1 ! n i ! = N ! ∏ i = 1 M 1 n i ! \prod_{i=1}^{M} C^{n_i}{N_i} = \prod {i=1}^{M} \frac{N_i!}{(N_i-n_i)!\ n_i!} = \prod_{i=1}^{M} \frac{N_i!}{N_{i-1}!\ n_i!} = N! \prod_{i=1}^{M} \frac{1}{n_i!} i = 1 ∏ M C N i n i = i = 1 ∏ M ( N i − n i )! n i ! N i ! = i = 1 ∏ M N i − 1 ! n i ! N i ! = N ! i = 1 ∏ M n i ! 1
个,此亦即归一化系数的来源。
这里采用的分析方法是对全同粒子进行人为编号, 写出波函数的每一项, 然后把它们适当线性叠加, 进而构造满足交换对称性要求的波函数。但实际上这一编号没有意义,更简单的做法是使用二次量子化(second quantization)方法,即粒子填布数(occupation number)表象,用单粒子态上的粒子占有数表示, ∣ n 1 n 2 ⋯ n M ⟩ = ∣ n 1 ⟩ ∣ n 2 ⟩ ⋯ ∣ n M ⟩ | n_1n_2 \cdots n_M \rangle = | n_1 \rangle | n_2 \rangle \cdots | n_M \rangle ∣ n 1 n 2 ⋯ n M ⟩ = ∣ n 1 ⟩ ∣ n 2 ⟩ ⋯ ∣ n M ⟩ ψ 1 , ψ 2 , ⋯ , ψ M \psi_1,\psi_2,\cdots,\psi_M ψ 1 , ψ 2 , ⋯ , ψ M n 1 , n 2 , ⋯ , n M n_1,n_2,\cdots,n_M n 1 , n 2 , ⋯ , n M n 1 n 2 ⋯ n M n_1n_2 \cdots n_M n 1 n 2 ⋯ n M Ψ S \Psi^S Ψ S
由于Fermi子受Pauli不相容原理的限制,一个量子态上只能有一个Fermi子,故设 N N N k 1 , k 2 , ⋯ , k N k_1,k_2,\cdots,k_N k 1 , k 2 , ⋯ , k N
Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = 1 N ! ∣ ψ k 1 ( q 1 ) ψ k 1 ( q 2 ) ⋯ ψ k 1 ( q N ) ψ k 2 ( q 1 ) ψ k 2 ( q 2 ) ⋯ ψ k 2 ( q N ) ⋮ ⋮ ⋱ ⋮ ψ k N ( q 1 ) ψ k N ( q 2 ) ⋯ ψ k N ( q N ) ∣ \Psi^A_{k_1k_2 \cdots k_N} (q_1,q_2,\cdots,q_N) = \frac{1}{\sqrt{N!}} \begin{vmatrix} \psi_{k_1}(q_1) & \psi_{k_1}(q_2) & \cdots & \psi_{k_1}(q_N) \ \psi_{k_2}(q_1) & \psi_{k_2}(q_2) & \cdots & \psi_{k_2}(q_N) \ \vdots & \vdots & \ddots & \vdots \ \psi_{k_N}(q_1) & \psi_{k_N}(q_2) & \cdots & \psi_{k_N}(q_N) \ \end{vmatrix} Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = N ! 1 ψ k 1 ( q 1 ) ψ k 2 ( q 1 ) ⋮ ψ k N ( q 1 ) ψ k 1 ( q 2 ) ψ k 2 ( q 2 ) ⋮ ψ k N ( q 2 ) ⋯ ⋯ ⋱ ⋯ ψ k 1 ( q N ) ψ k 2 ( q N ) ⋮ ψ k N ( q N )
此式称为Slater行列式 ,也可以表示为
Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = A ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) ⋯ ψ k N ( q N ) \Psi^A_{k_1k_2 \cdots k_N} (q_1,q_2,\cdots,q_N) = \mathcal{A} \psi_{k_1}(q_1) \psi_{k_2}(q_2) \cdots \psi_{k_N}(q_N) Ψ k 1 k 2 ⋯ k N A ( q 1 , q 2 , ⋯ , q N ) = A ψ k 1 ( q 1 ) ψ k 2 ( q 2 ) ⋯ ψ k N ( q N )
其中反对称算符
A = 1 N ! ∑ P ^ δ P ^ P ^ \mathcal{A} = \frac{1}{\sqrt{N!}} \sum_{\hat{P}} \delta_{\hat{P}} \hat{P} A = N ! 1 P ^ ∑ δ P ^ P ^
式中的 P ^ \hat{P} P ^ N ! N! N ! I ^ \hat{I} I ^ δ P ^ = − 1 \delta_{\hat{P}} = -1 δ P ^ = − 1 δ P ^ = 1 \delta_{\hat{P}} = 1 δ P ^ = 1