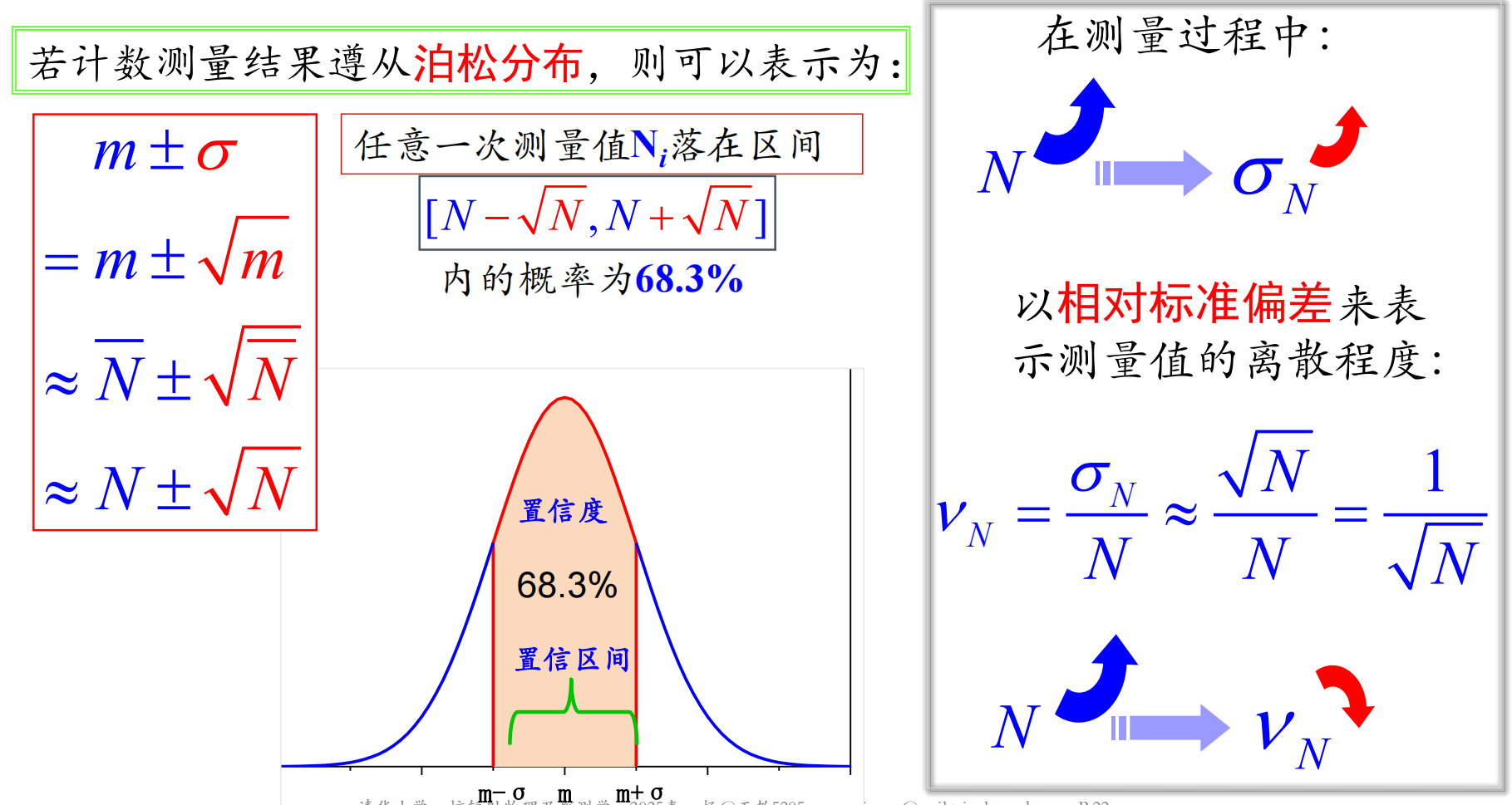
- 计数测量值标准偏差( Ni 为计数测量值,满足泊松分布 )
σ=m=N=Ni
- 计数测量值相对标准偏差( Ni 为计数测量值,满足泊松分布 )
ν=mσ=m1=Ni1
- 计数率
n=tN
其标准偏差
σn=tn
其相对标准偏差
νn=nσn=nt1=N1
- 净计数率( ns 为样品总计数率,即本底与源之和, ts 为样品测量时间;nb 为本底计数率, tb 为本底测量时间 )
n0=ns−nb=tsNs−tbNb
其标准偏差
σn0=tsns+tbnb
其相对标准偏差
νn0=ns−nb1tsns+tbnb
- 在规定的总测量时间 T=ts+tb 内使测量结果误差最小时,得到最佳测量条件(时间分配) 为
tbts=nbns ts=1+ns/nbns/nbT,tb=1+ns/nb1T
在最佳测量条件下得到的测量结果——净计数率的相对方差( T 内测量可得的最小值)为:
νn02=[ns−nb1tsns+tbnb]2=Tnb(ns/nb−1)21=T(ns−nb)21
在 νn0 给定的情况下,需要的最小测量时间为
Tmin=nbνn02(ns/nb−1)21=νn02(ns−nb)21
- 电离室( F 为法诺因子)
η=2.355NF=2.355EFW
- 正比计数器( νA2=0.68 为气体放大系数的相对方差 )
η=2.355NF+0.68
- 闪烁探测器( ne=EYphT 为第一打拿极收集到的光电子数)
η=2.355ne1[1+δ1δ(δ−11)]
- 半导体探测器
η=2.355NF=2.355EFW
- 能量分辨率的两种表示(以电离室或半导体探测器为例,只考虑统计涨落)
η=EFWHM=2.355EFW×100%
- 用半高宽(线宽)表示(一般 W 单位为 eV , E 单位为 MeV ,此时 ΔE 单位为 keV ):
ΔE=FWHM=2.355F⋅W⋅E
- 当考虑影响分辨率的各种影响因素时,谱仪总分辨率为
ΔE=FWHM=i∑ΔEi2
- 电荷灵敏前置放大器的噪声
ΔEnoise=ΔE零电容+ΔE电容噪声=ΔE零电容+噪声斜率×探测器电容
或
ΔEnoise=2.355⋅W⋅ENC
- 放大器的信噪比( h1 为信号幅度, σh2 为噪声的标准偏差)
J=σh2h1
放大器噪声对能量分辨率的影响(以电离室为例)
η=2.355NF+J21×100%

-
准确度(accuracy):
- 测量值与被测对象真值的一致程度。
- 由测量值的平均值与真值的差来描述。
-
精密度(precision):
- 测量的可重复性或可靠性。
- 可用测量的均方偏差来描述。
数学期望
E(ξ)=i=1∑N或∞xi⋅f(xi) E(X)=∫−∞+∞x⋅f(x) dx
均方偏差,简称为方差
D(ξ)=i=1∑N或∞[xi−E(ξ)]2⋅f(xi) D(X)=∫−∞+∞[x−E(X)]2⋅f(x) dx
均方根偏差
σ=D
相对均方偏差
ν2=E2D
相对均方根偏差
ν=Eσ
若 x1,x2,⋯,xn 是相互独立的随机变量,各随机变量相应的标准偏差分别为 σx1,σx2,⋯,σxn ,那么由这些随机变量导出的任何量 y=f(x1,x2,⋯,xn) 的均方偏差为
σy2=(∂x1∂y)2σx12+(∂x2∂y)2σx22+⋯+(∂xn∂y)2σxn2
几个简单函数的标准偏差及相对标准偏差如表所示:
| 函数 f | 标准偏差 | 相对标准偏差 |
|---|
| y=ax1±bx2 | [(aσx1)2+(bσx2)2]21 | [(aσx1)2+(bσx2)2]21/(ax1±bx2) |
| y=x1⋅x2 | x1⋅x2[(x1σx1)2+(x2σx2)2]21 | [(x1σx1)2+(x2σx2)2]21 |
| y=x1/x2 | x2x1[(x1σx1)2+(x2σx2)2]21 | [(x1σx1)2+(x2σx2)2]21 |
E(C⋅ξ)=C⋅E(ξ) D(C⋅ξ)=C2⋅D(ξ) ν2(C⋅ξ)=[E(ξ)]2D(ξ)
E(ξ1±ξ2±⋯±ξn)=E(ξ1)±E(ξ2)±⋯±E(ξn) D(ξ1±ξ2±⋯±ξn)=D(ξ1)+D(ξ2)+⋯+D(ξn)
E(ξ1⋅ξ2⋯ξn)=E(ξ1)⋅E(ξ2)⋯E(ξn) D(ξ1⋅ξ2⋯ξn)=(ξ1⋅ξ2⋯ξn)2[(ξ12D(ξ1))2+(ξ12D(ξ1))2+⋯+(ξ12D(ξ1))2] ν2(ξ1⋅ξ2⋯ξn)=ν2(ξ1)+ν2(ξ2)+⋯+ν2(ξn)
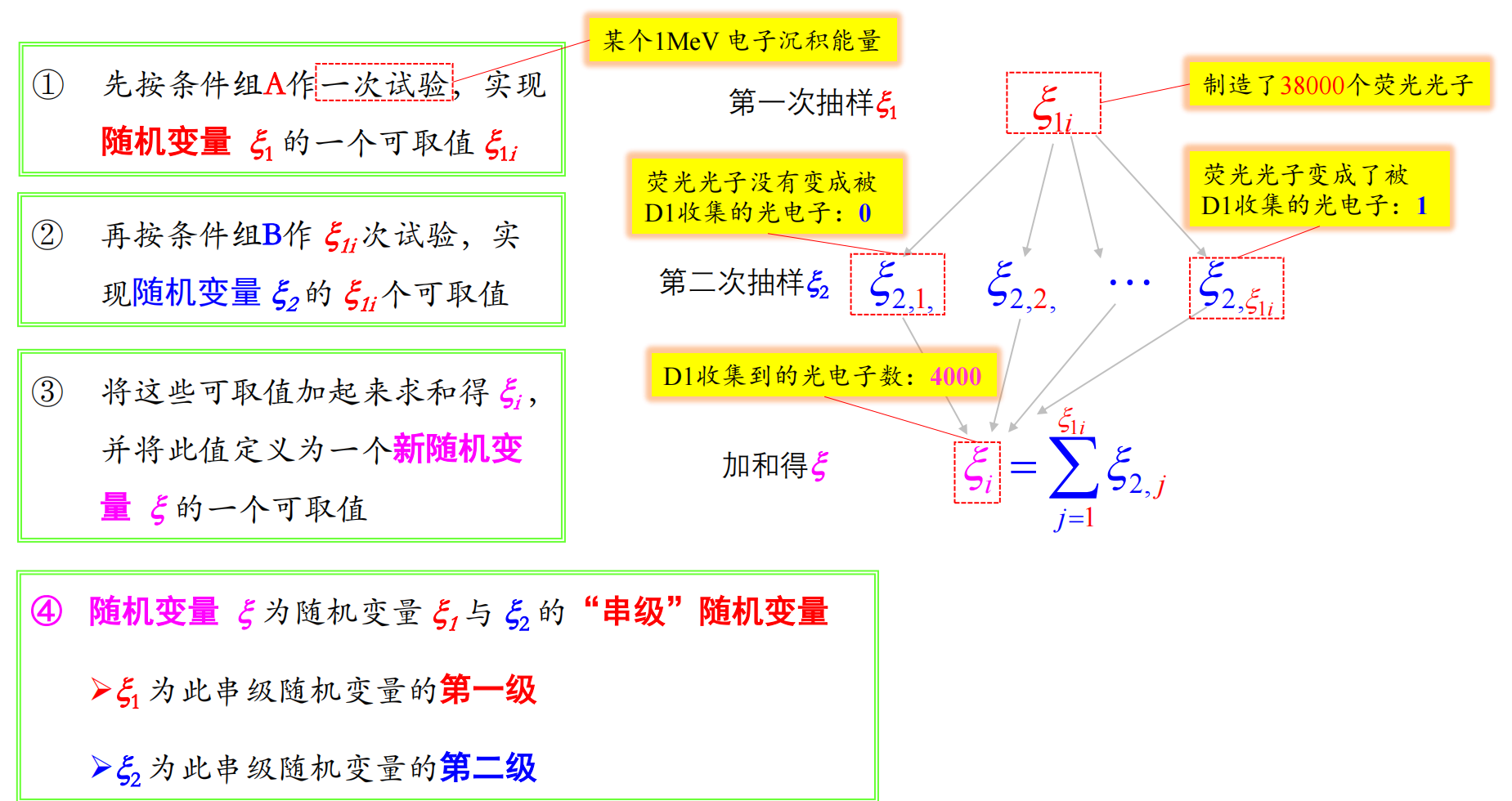
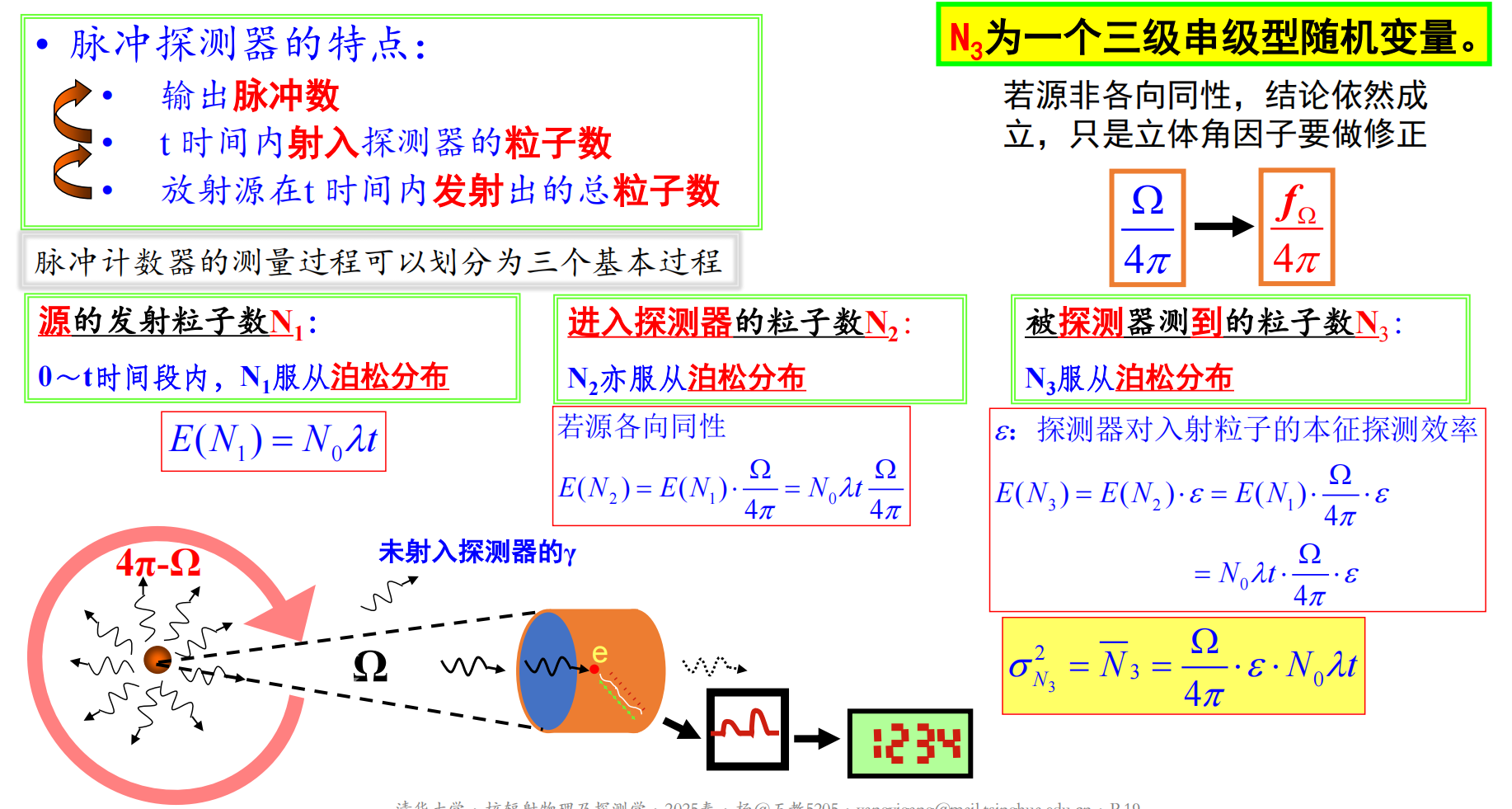
E(ξ)=E(ξ1)⋅E(ξ2) D(ξ)=[E(ξ2)]2⋅D(ξ1)+E(ξ1)⋅D(ξ2) νξ2=[E(ξ)]2D(ξ)=νξ12+E(ξ1)1νξ22
若第一级随机变量的数学期望很大,则可忽略第二级随机变量的相对方差对串级随机变量的相对方差的贡献。
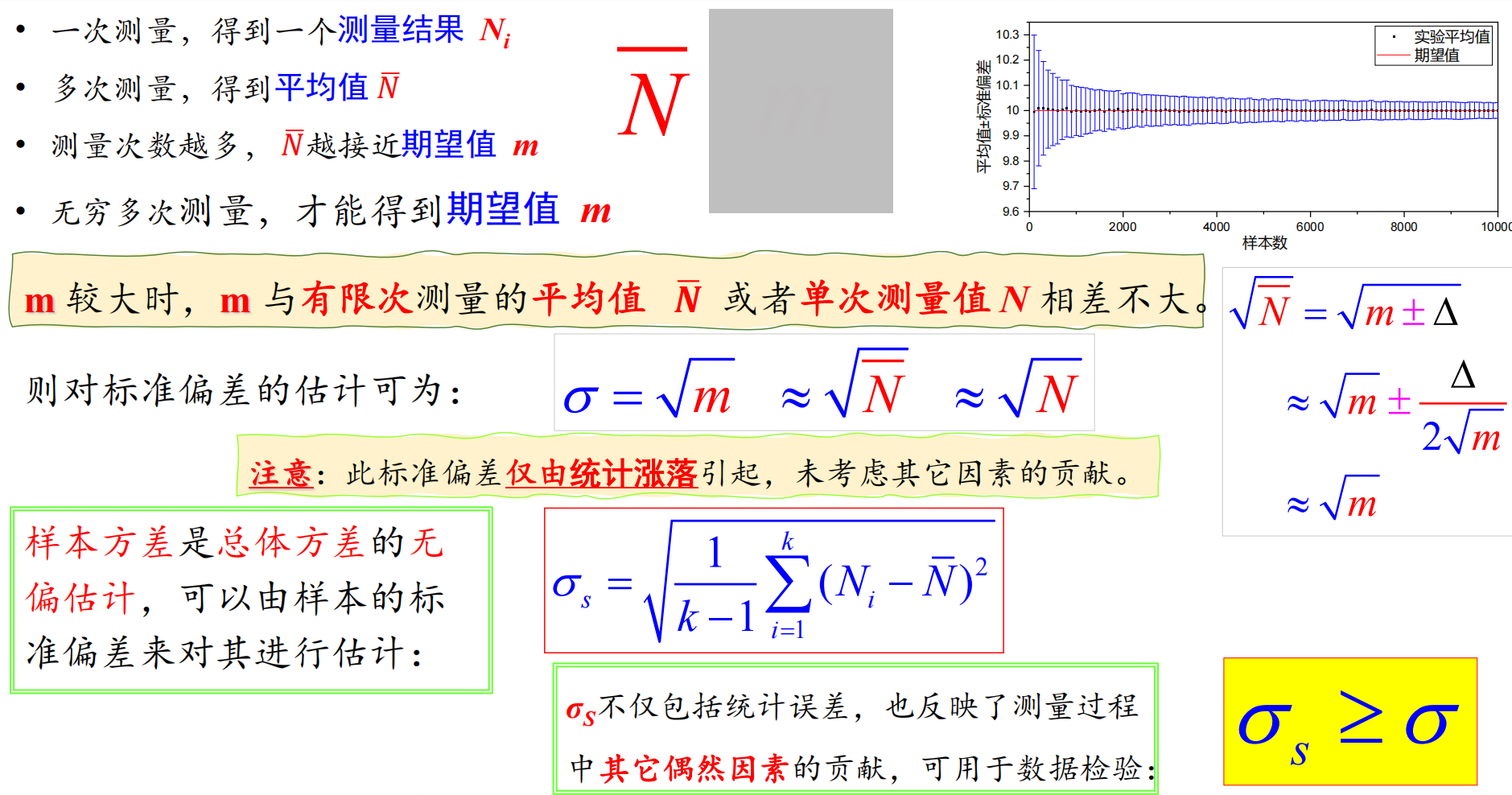
E(ξ)=E(ξ1)⋅E(ξ2)⋯E(ξN) νξ2=νξ12+E(ξ1)νξ22+E(ξ1)⋅E(ξ2)νξ32+⋯+E(ξ1)⋅E(ξ2)⋯E(ξN−1)νξN2
对计数率进行 k 次独立测量,各次测量的时间 ti 不同,计数为 Ni ,得到不同的 ni ,则计数率的加权平均值
n=∑iti∑itini=∑iti∑iNi
标准偏差
σn=∑iti∑iσNi2=∑iti∑iNi=∑itin
相对标准偏差
νn=nσn=∑iNi1
就统计误差而言,无论是一次测量还是多次测量,只要总的计数相同,多次测量平均计数率的相对误差和一次测量的计数率的相对误差是一致的。
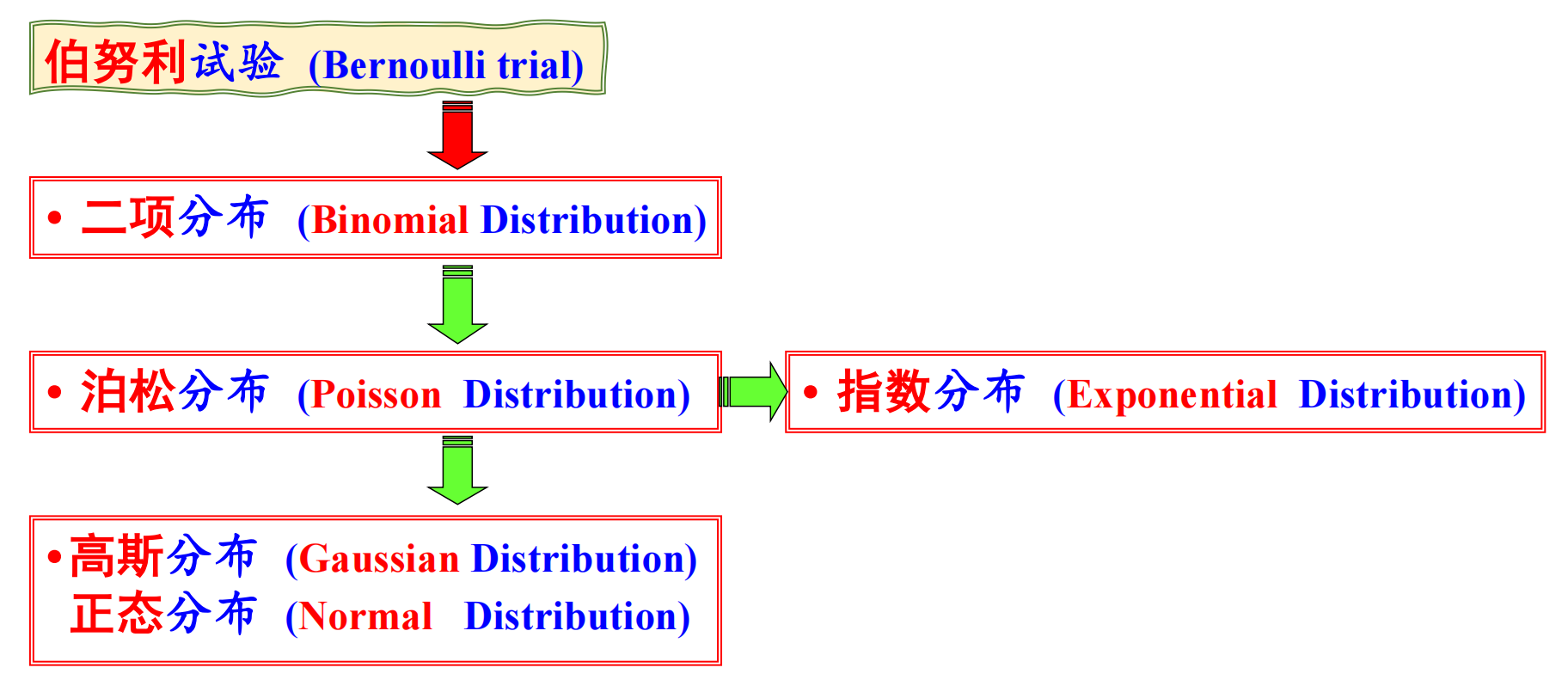
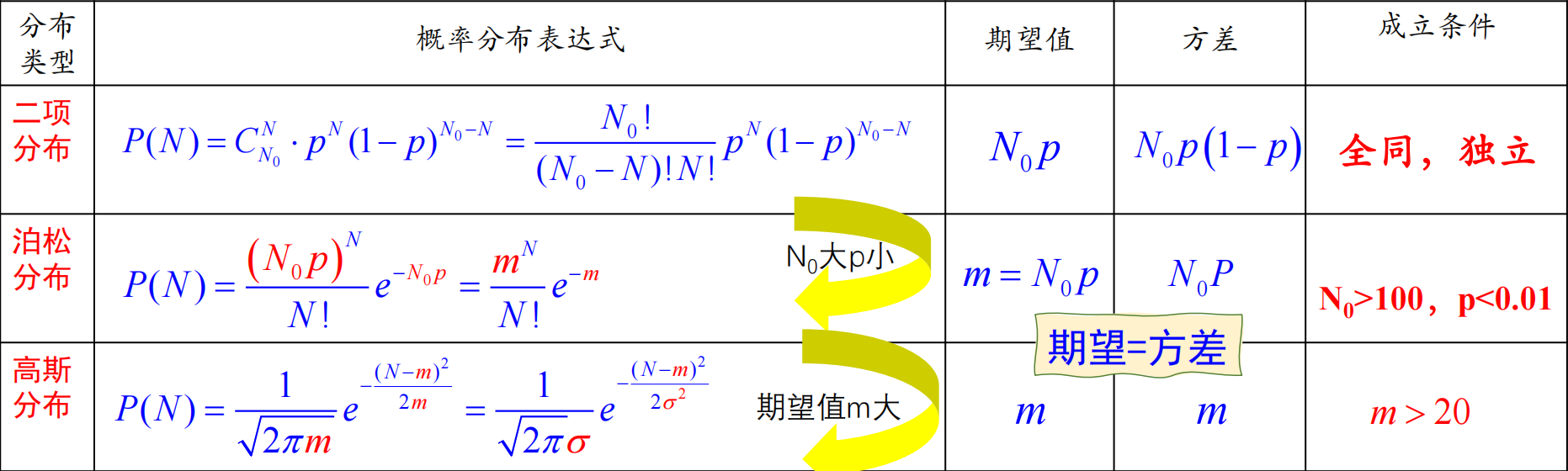
核衰变在任何情况下严格服从二项式分布:
p=1−e−λt
当 λt很小时,核衰变服从泊松分布:
m=σ2=N0⋅λ⋅t
当 m>20 时,满足高斯分布(正态分布),高斯分布本身不具有期望与方差相等的特征,若是从泊松分布演化而来,则满足期望与方差相等。
伯努利串级伯努利仍为伯努利:
p=p1⋅p2 E(ξ)=E(ξ1)⋅E(ξ2) νξ2=p11−p1+p11p21−p2=p1p21−p1p2
泊松串级伯努利仍为泊松:
E(ξ)=m1⋅p2 νξ2=m11+m11p21−p2=m1p21
相互独立的服从泊松分布的随机变量之和服从泊松分布:
E(ξ1+ξ2)=E(ξ1)+E(ξ2) D(ξ1+ξ2)=D(ξ1)+D(ξ2)
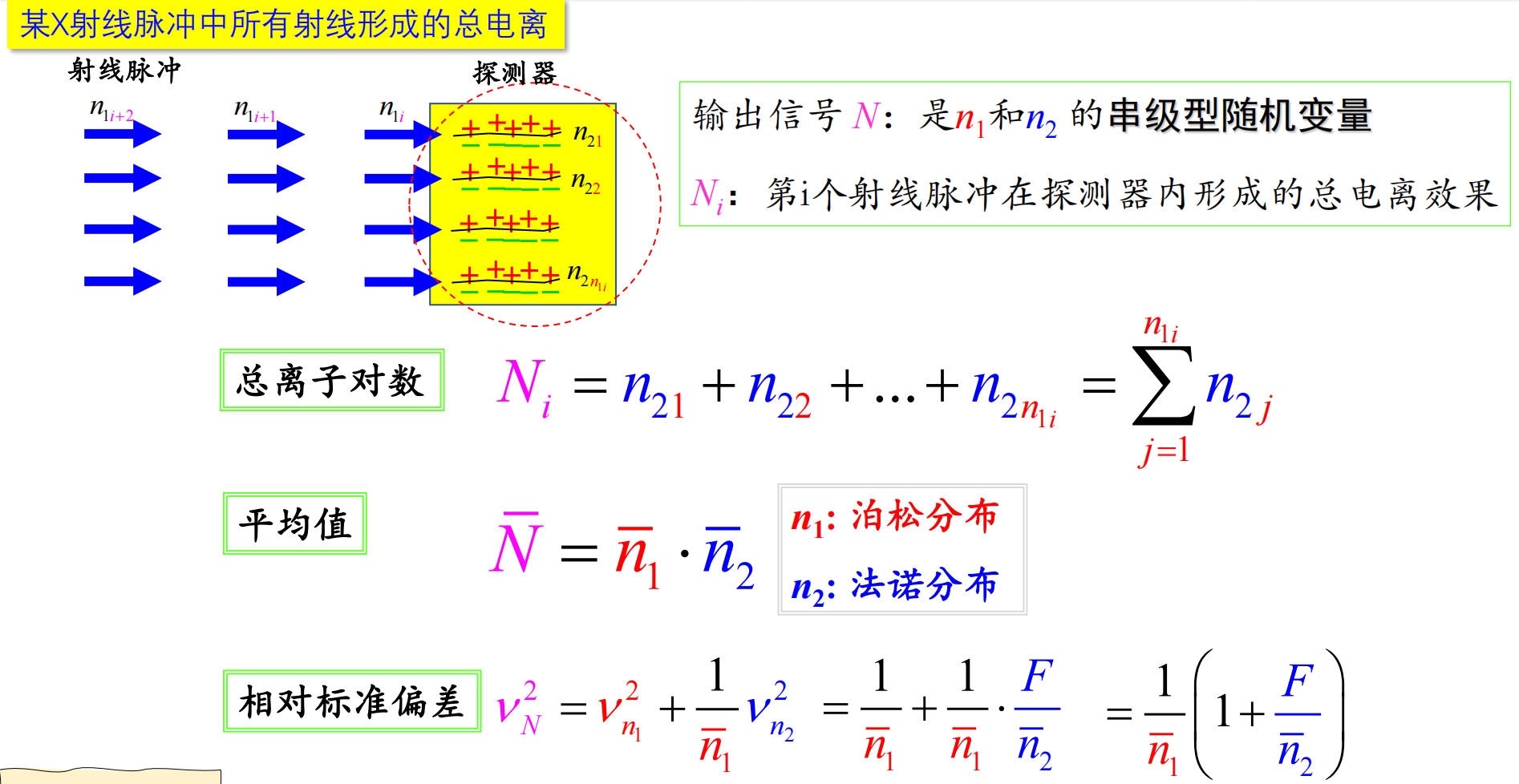
由于带电粒子在气体中总的碰撞次数是不确定的,且碰撞过程是不独立的,故带电粒子在气体中电离产生的总电子离子对数不能简单用泊松分布描述,而应使用法诺分布,法诺因子
F=nσ2
气体的法诺因子一般在 31∼21 之间,半导体的法诺因子一般在 0.1∼0.15 之间。法诺分布的方差即相对反差为
σ2=F⋅n=F⋅WE ν2=nF=EF⋅W
第一次,在时间 tb 内测得本底的计数为 Nb ,得到本底计数率 nb=Nb/tb ;第二次,在时间 ts 内测得样品和本底的计数为 Ns ,得到本底计数率 ns=Ns/ts 。则样品的净计数率
n0=ns−nb=tsNs−tbNb
其标准偏差为
σn0=tsns+tbnb
其相对标准偏差为
νn0=ns−nb1tsns+tbnb
在规定的总测量时间 T=ts+tb 内使测量结果误差最小时,得到最佳测量条件(时间分配) 为
tbts=nbns ts=1+ns/nbns/nbT,tb=1+ns/nb1T
在最佳测量条件下得到的测量结果——净计数率的相对方差( T 内测量可得的最小值)为:
νn02=[ns−nb1tsns+tbnb]2=Tnb(ns/nb−1)21=T(ns−nb)21
在 νn0 给定的情况下,需要的最小测量时间为
Tmin=nbνn02(ns/nb−1)21=νn02(ns−nb)21
若 nb≫n0 ,则
Tmin→νn02n024nb
这表明降低本底可以实现节省测量时间的作用。
相邻脉冲信号时间间隔为 t 的概率
f(t)=m⋅e−m⋅t
其中 m 为单位时间内的平均信号脉冲数。由此可知相邻脉冲信号时间间隔满足指数分布,且接收到一个信号后,在当前时刻接收到下一个信号的可能性最大。
相邻脉冲信号时间间隔的平均值、方差及相对均方根偏差分别为
t=∫0+∞t⋅f(t) dt=m1 σt2=∫0+∞(t−t)2⋅f(t) dt=m21 νt=tσt=1
在计数率较高时,需要使用具有进位系数 S 的定标器来计数。每接受来自探测器的 S 个信号,定标器产生一个进位信号脉冲。相邻进位脉冲的时间间隔为 t 的概率
fS(t)=(S−1)!(mt)S−1me−mt
使得 f(t) 取值最大的值 tS 为
tS=mS−1
相邻进位脉冲时间间隔的平均值、均方根偏差及相对均方根偏差分别为
TS=mS σTS2=m2S νTS=S1
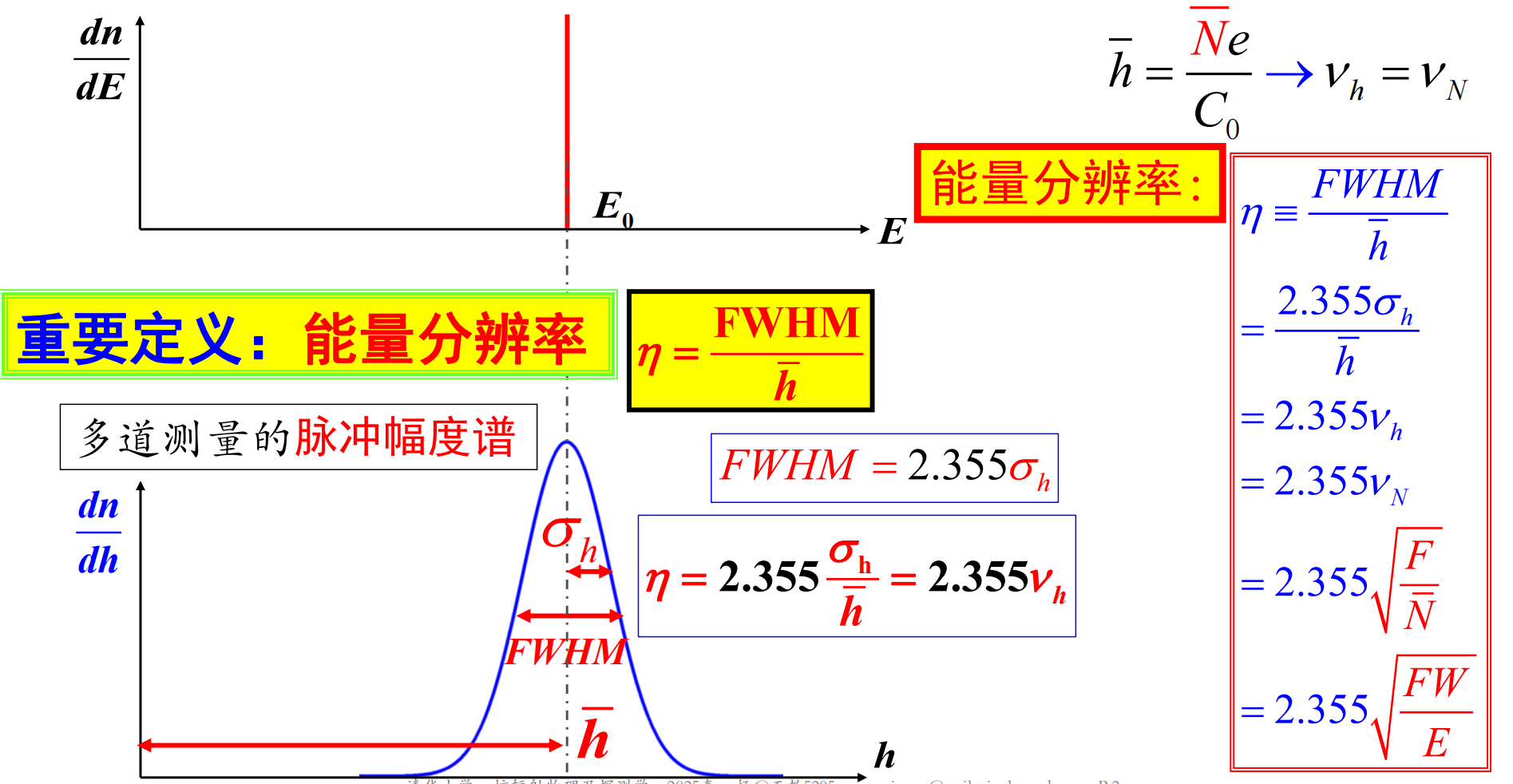
定义能量分辨率为
η=EΔE×100%=hΔh×100%
式中 ΔE 表示能谱半高宽,即谱峰极大值一半处的全宽度,缩写符号为 FWHM 。
(ΔE)2=FWHMtotal2=i∑(ΔEi)2=i∑FWHMi2 =FWHMstatistical2+FWHMdrift2+FWHMnoise2+⋯
综合考虑放大器放大倍数 A 的涨落,放大器噪声的影响,则电离室谱仪放大器输出信号器输出信号的相对均方涨落为
νhA2=EF⋅W+νA2+J21
能量分辨率为
η=2.355EF⋅W+νA2+J21×100%
因为统计涨落必然存在,所以能量分辨率不可能为 0 。
ηstatistical=2.355EF⋅W FWHMstatistical=2.355F⋅W⋅E
其中 F⋅W 与探测器类型有关, E 为射线沉积的能量。
信号幅度 h0 经过放大器放大后输出的脉冲幅度为 Ah0 ,这里 A 为放大器的放大倍数,是一个连续型随机变量。
综合考虑statistical与drift,则相对均方涨落
νhA2=EF⋅W+νA2
放大器噪声( h2 )对输出幅度涨落的影响是叠加关系
h=h1+h2
综合考虑statistical与drift,则相对均方涨落
νh2=h12σh12+h22σh22=EF⋅W+J21
其中放大器的信噪比定义为
J=σh2h1
能量分辨率为
η=2.355NF=2.355EFW×100%
电流电离室输出电流信号的平均值和相对均方涨落为
I=n⋅N⋅e νI2=n⋅T1+NF≈n⋅T1
输出电压信号的平均值和相对均方涨落为
I=n⋅N⋅e⋅R0=I0R0 νV2=2R0C0n1+NF≈2R0C0n1
累计信号的相对均方涨落有如下特点:
- 主要决定于入射粒子数 n 的涨落
- 离子对数 N 的涨落的影响很小
正比计数器的输出脉冲幅度 h 是一个二级串级型随机变量
h∼C0NAe
相对均方涨落为
νh2=νN2+N1νA2=NF+N1νA2
其中实验测得 νA2≈0.68 ,故能量分辨率为
η=2.355NF+0.68×100%
光电倍增管PMT的倍增系数 M 的相对均方涨落为
νM2=δ1δ(δ−11)
其中 δ1 为第一打拿极的倍增因子, δ 为第一打拿极外其余各打拿极的倍增因子。
能量分辨率为
η=2.355ne1[1+δ1δ(δ−11)]
其中 ne=EYphT 为第一打拿极收集到的光电子数。
只考虑统计涨落的能量分辨率为
η=2.355NF=2.355EFW
考虑电荷灵敏前置放大器的噪声:
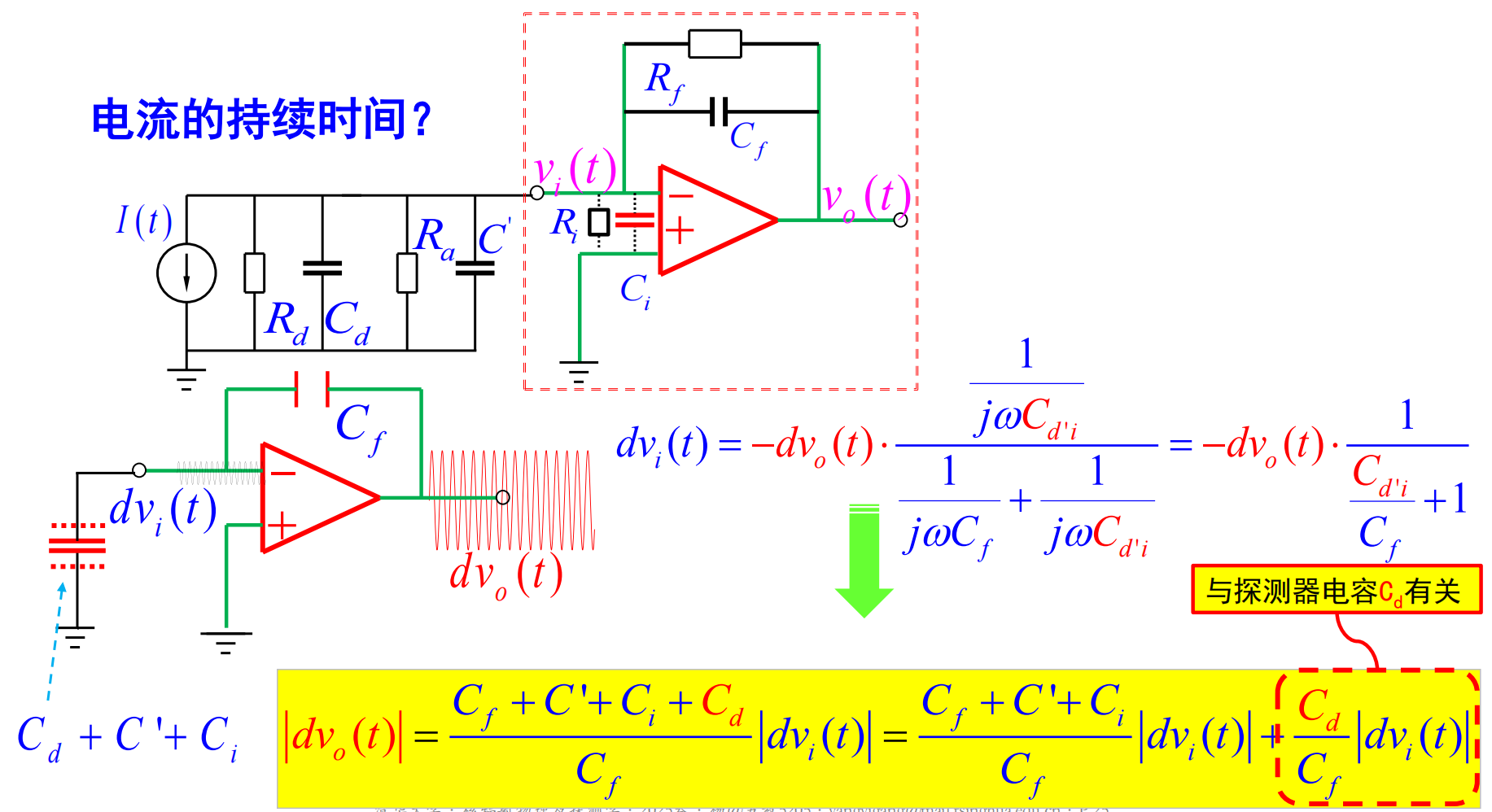
ΔEnoise=ΔE零电容+ΔE电容噪声=ΔE零电容+噪声斜率×探测器电容
也可以用等效噪声电荷 ENC 来表示,以电子电荷为单位,其含义为放大器输出端噪声电压均方根值等效到输入端的电荷数,则
ΔEnoise=2.355⋅W⋅ENC